三峡区间面雨量空间插值方法对比分析
王汉东,黄瓅瑶,朱思蓉,罗 斌
(长江勘测规划设计研究有限责任公司,湖北 武汉 430010)
0 引言
作为一项重要的流域降雨强度特征指标,流域面雨量是进行防洪形势分析、水文预报的重要因子之一,流域面雨量的计算直接关系到洪水预报的精度[1]。
流域面雨量的一种简单计算方法是用流域范围内各雨量站的雨量平均值作为流域面雨量[2]。然而降雨具有时空不连续性的特点,雨量站的实测雨量属于点雨量,只可代表该测站周围局部区域的平均降雨量,无法准确反映更大范围的降雨情况。因此,流域面雨量的估算可以归结为如何根据有限数量的雨量站观测值推算整个流域的降雨情况。流域面雨量常用的计算方法是空间插值算法[3–5],空间插值是根据少量的已知空间样点数据估计未知空间的数据值,可以分为确定性和地统计 2 种插值算法[6]:确定性插值利用对象的空间相似性,或以平滑度为基础,根据已知样本点创建表面;地统计插值则不仅考虑对象的空间相关性和依赖性,还考虑对象的统计特性,如频率分布、方差、均值等。地统计插值能够量化样本点之间的空间自相关性,并揭示其空间分布。
用于面雨量计算的空间插值方法较多,每种插值方法都有相应的适用条件,同一区域采用不同的插值方法,计算结果会有一定程度的差异。因此,需要根据雨量站点的分布情况及流域地形特征等因素选择合适的插值方法[7]。本研究分别选取反距离加权、普通克里金、协同克里金 3 种插值方法,应用于三峡区间的面雨量计算,通过计算结果的对比,分析产生差异的原因,从而找到三峡区间流域最为合适的面雨量插值方法。
1 流域面雨量的概念介绍
流域面雨量是流域内的平均降雨量,计算公式如下:

流域范围内的雨量站数量有限,因此面雨量的实际计算是将式 (1) 离散化,先根据雨量站的位置和数量将流域划分为N个小区域,每个小区域仅包含1 个雨量站,用第i个小区域上的雨量站的雨量(点雨量)Pi代表该区域的平均降雨量,则流域面雨量近似计算如下:

式中:Ai为第i个小区域面积。
2 流域面雨量插值方法分析及精度评定
2.1 反距离加权插值
反距离加权插值是一种确定性空间插值方法,以对象点之间的空间距离为权重,距离越近,权重越大。插值点雨量估计值P的计算公式如下:

式中:n为已知样本点的数量;P(si) 是样本点si处的降雨量值;ωi是样本点si的权重。权重ωi的计算公式如下:

式中:p为指数值,用于控制插值点与已知样本点之间的距离对插值结果的影响;di为预测点s与已知样本点si之间的距离。
p一般为正实数,指数值越大,距离越近的样本点对结果的影响越大,可进一步强化距离近的样本点对插值结果的影响。指数值减小,距离远的样本点对结果的影响增强,距离对插值结果的影响会弱化。本研究中p的取值为 2,这也是最常用的取值。
2.2 普通克里金插值
普通克里金插值利用区域化变量的原始数据和变异函数的结构特点,对未知样点进行线性无偏、最优化估计。计算公式如下:

式中:P(x0) 为x0点处估计降雨量;P(xi) 为第i站的实测降雨量;ωi为第i个观测点对插值点的权重;n为实测雨量站的数量。
建立空间变量的协方差函数,提出变异函数模型是普通克里金插值计算重要的一环。最常用的变异函数模型有球面、指数、高斯、幂和线性模型,本研究根据方差变异分析结果,选用球面模型作为普通克里金的变异函数理论模型。
2.3 协同克里金插值
协同克里金插值法是在普通克里金插值法的基础上引进对结果有影响的相关因素进行插值的一种方法,通过用 1 个或多个辅助变量对主变量进行插值估算,从而把区域化变量的最佳估值方法从单一属性发展到 2 个或 2 个以上的协同区域化属性。地理、气象等多种要素对流域面雨量均有不同程度的影响,因此,在面雨量计算的过程中充分考虑上述影响因子,有助于提高插值计算的精度。
将流域地形作为降雨插值相关的辅助变量,考虑高程影响的协同克里金插值可用下式表示:

式中:y(xi) 为xi点处的高程;mh,mP分别为高程和降雨的全局平均值;λi为第i个站点的综合权重。λi计算如下:个权重对第i个站点的权重;γ为

式中:λij为第jij第i个站点的每j个单个权重因子。利用这种综合权重计算方法,可定量表示出不同权重因子对降雨量的影响。
2.4 面雨量计算精度评定
流域面雨量无法通过观测手段得到,不能通过实际观测值进行验证,因此常采用交叉验证法验证插值效果[8]。采用平均误差δ、平均绝对误差γ、误差均方根σ作为评估插值效果的标准。δ总体反映估计误差的大小,γ可以估量估计值可能的误差范围,σ可以反映利用样点数据估值的灵敏度和极值效应,相关计算公式如下:
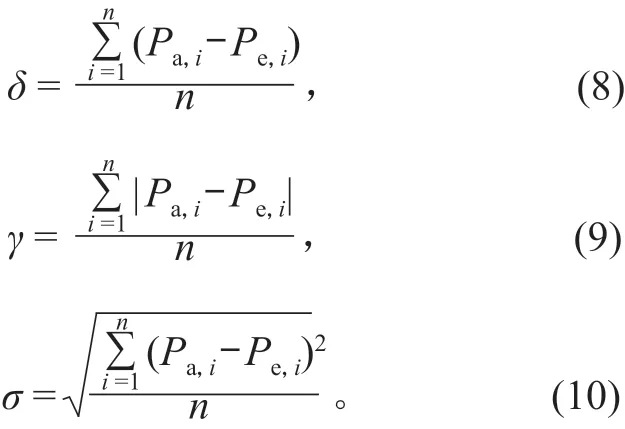
式中:Pa,i为第i个站点的实际观测值;Pe,i为第i个站点的估计值;n为用于检测的站点数量。
3 流域面雨量的研究结果分析
三峡区间一般是指长江干流寸滩、支流乌江武隆至三峡坝址之间的区域,位于长江流域上游最下端,三峡区间长江干流河长为 614 km,区间面积为 5.3 万 km2。三峡区间属北温带和亚热带季风气候的过渡带,年降水量在 1 000~1 600 mm 之间,年内降水大多集中在 6—9 月。受大巴山、巫山地形影响,三峡区间暴雨发生频繁,降雨强度大。三峡区间高程在 66~3 393 m 之间,地形复杂,支流众多。本研究降雨数据选取三峡区间 309 个雨量站2017 年的日降雨数据,三峡区间 DEM 及雨量站分布如图 1 所示。
使用反距离加权等 3 种插值方法对三峡区间2017 年 6 月 3 日 2 时至 6 日 8 时的一场降雨进行面雨量空间插值计算,采用反距离加权、普通克里金、协同克里金 3 种插值方法计算得到的整个区间流域的面雨量分别为 56.4,57.8 和 57.2 mm,3 种插值方法的插值结果如图 2 所示。
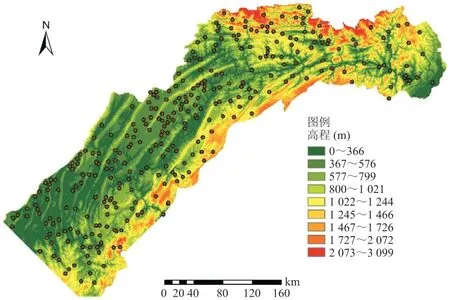
图 1 三峡区间 DEM 及雨量站分布
3.1 面雨量空间分布特征分析
从图 2 可以看出:3 种插值方法得到的面雨量空间分布特征总体上较为接近,仅在局部空间分布上存在差异。最大降雨主要分布在流域北部,这与地面雨量站的分布、实际观测值基本吻合,也与三峡区间的地理与气候特征吻合。从图 1 可以看出:三峡区间北部的分水线地形高程高于南部,在夏季,季风从西南方向进入,在流域北部的迎风面上会产生高强度的地形雨,形成暴雨中心。另外,从图 2 a 和 2 b 可以看出:除了北部的主中心外,还有 2~3 个副中心点,在图 2 a 中更为明显,这是因为反距离加权插值以对象之间的距离为权重,样本点离插值点越近则权重越大,影响越大。从总体上看,2 种克里金插值的结果均比反距离加权插值的结果平滑,这是由于克里金插值方法不仅考虑雨量站对象之间的空间相关性,还考虑雨量站之间的依赖关系。


图 2 3 种插值方法的面雨量插值预测结果图
3.2 计算结果精度评定
3 种空间插值方法的面雨量计算结果存在一定程度的差异,采用交叉验证方法对结果进行评定,评价指标包括δ,γ和σ,精度分析如表 1 所示。

表 1 3 种插值方法的精度分析 mm
从表 1 可以看出,反距离加权插值的δ,γ,σ均高于 2 种克里金插值方法。这是因为反距离加权插值方法侧重于距离的影响,距离越近,地理对象之间的相似性越大,但是,该方法无法准确反映相邻站点之间的空间依赖关系,也无法考虑各种地形对面雨量的影响,因此插值效果较差。克里金插值法充分考虑空间对象之间的相关性和依赖关系,因而插值精度有较大的提高。
另外,相对于普通克里金插值法,协同克里金插值法在进行面雨量插值的过程中,充分融合了数字高程模型数据,将高程数据作为辅助变量提高插值精度。从表 1 可以看出:相对于普通克里金插值法,协同克里金插值法的γ和σ分别降低了 19%,10%,插值精度有一定程度的提高。
4 结语
将反距离加权、普通克里金、协同克里金 3 种空间插值方法应用于三峡区间的面雨量插值计算,通过比较 3 种插值方法的插值效果,分析 3 种插值方法精度差异的原因,可以得到以下针对三峡区间的面雨量插值计算结果:2 种克里金插值法的插值结果的误差要小于反距离加权插值法,并且插值效果更平滑;对于 2 种克里金插值法,协同克里金插值的精度要优于普通克里金插值。复杂地形是影响降雨空间分布的一个重要因素,因此,在山区或地形起伏较大的区域进行面雨量空间计算时,考虑地形影响的协同克里金插值比普通克里金插值有更好的精度表现。
降雨具有时空分布特征,在面雨量插值计算过程中,应充分考虑各雨量站之间的空间自相关性和依赖性,这也是克里金插值比反距离加权插值有更高精度的原因;另外,流域面雨量也受气象、地形、雨量站数量及分布等多种因素的影响,应根据流域的具体情况,充分考虑各种影响因素,选择合适的面雨量插值算法。
对于给定的流域或区域,雨量站的数量和分布往往成为面雨量插值算法的前提和限定条件。随着现代雨量监测技术的发展,已有更多先进的雨量监测手段,如雷达测雨等,在面雨量计算过程中,引入数据融合技术,充分利用多源雨量监测数据,将会在一定程度上提高面雨量计算的精度。

