基于 LM-BP 神经网络的莺落峡河段糙率推测分析
朱 咏 ,陈学林
(1. 甘肃省张掖水文水资源勘测局,甘肃 张掖 734000;2. 甘肃省水文水资源局,甘肃 兰州 730000)
0 引言
在天然河道水利工程建设中,需要进行河道断面的水位-流量关系、水库回水、河道洪水演进等分析计算;在 GB 50179—2015《河流流量测验规范》中,明确提出比降-面积法可作为高洪测流的主要手段之一[1]。在这些计算过程中,糙率n是重要灵敏、无量纲的参数值,n值选择的合理与否直接影响计算结果的正确性[2]。到目前为止,没有较精确的公式可以用来求解n值,也无工具可以直接测量。天然河道糙率的基本含义是表征均匀流条件下阻力平方区内水流周界粗糙程度的系数,可衡量出河床形状不规则和粗糙程度对水流阻力的作用大小。实际应用过程中,大多是在恒定流条件下基于实测资料反推糙率值,但非恒定流情况复杂,难以从实测资料反求糙率[3]。
董文军等[4]根据参数辨识理论建立求解曼宁糙率的最优模型。程伟平[5]引入控制理论,应用带参数的卡尔曼滤波法求解圣维南非线性方程组,进行河道糙率反演分析。刘志贤[6]把河网中部分观测点的时间序列数据作为反演资料,提出将遗传算法应用于河网糙率值的反演计算过程。以上文献提到的糙率计算方法从糙率的物理意义出发,根据实测水文资料,采用优化方法反算糙率,主要应用于水力计算模型参数的确定。这些计算糙率值的新方法,有效克服了传统手工调试和经验估计等方法存在的不确定性、随机性的缺陷,但在应用过程中相对复杂。根据 Kolmogorov 定理,即具有一个隐层的三层BP 神经网络能在闭集上任意精度逼近非线性连续函数[7],LM-BP 神经网络是基于梯度下降和高斯-牛顿法结合的误差反向传播的预测模型,将其应用到测验河段糙率值推求方法中,需明确与糙率值相关度较大的输入量。
本研究基于 LM-BP 神经网络对莺落峡水文站测验河段的糙率值进行研究,应用该模型推测出的糙率值,可结合比降面积法较准确地计算出河道高洪水期流量。
1 天然河道糙率值计算分析
1.1 糙率值计算基本方法
目前由实测水文资料反推河床糙率的方法有以下 2 种:
1)恒定非均匀流。恒定非均匀流条件下,能量损失中不仅有沿程损失,还有局部损失。总能量损失中需把局部损失扣除,用沿程损失求糙率。最终可得糙率计算公式:
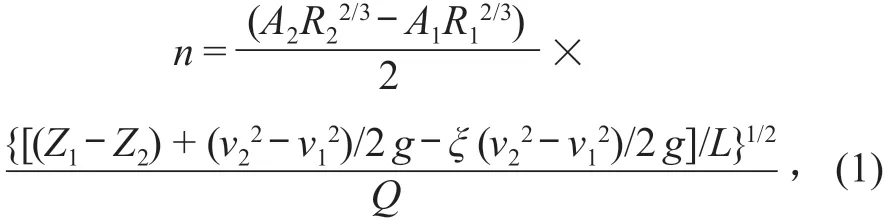
式中:A1和A2分别为上、下断面过水面积;R1和R2分别为上、下断面水力半径;Z1和Z2分别为上、下断面水位;v1和v2分别为上、下断面平均流速;L为上、下比降断面间距;ξ为局部摩阻系数;g为重力加速度;Q为断面流量。
2)恒定均匀流。恒定均匀流条件下,曼宁公式为
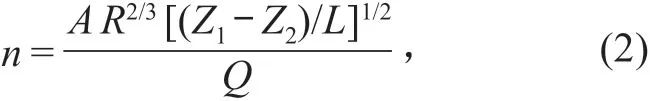
式中:A为断面面积;R为水力半径。
实际应用时,在天然河道控制断面处的流量测验过程中水位基本稳定,可近似为恒定流。应用实测资料,采用曼宁公式反推n值,需设有上、下比降断面和中断面,所观测的比降为上下比降断面间的平均比降;水位和流量均为中断面处的瞬时值。计算出的n值不只是单纯反映水流边界的粗糙程度,而是包括水流对河床反作用的影响、植被情况、断面几何形状、水力条件变化,以及比降观测、流量测验的测量误差影响因素在内的一个综合系数[8–9]。通常Z-n点据关系比较散乱,在不同水位情况下,难以确定一个较准确的值,最终导致计算出的流量误差偏大。
1.2 糙率值主要影响因素
李榕[10]探讨了影响糙率系数的水力因素,得出弗劳德系数F r和平均水深与水力半径R的比值对糙率系数起着决定性的作用,在雷诺系数Re 较大时,糙率系数的回归方程式可表示为
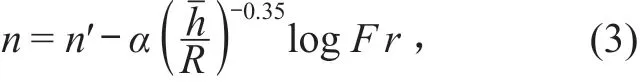
式中:n′ 为F r= 1 时的n值;α为系数,与n′ 有关。
何建京等[11]研究明渠不同水流流动型态对糙率系数的影响,得出非均匀流糙率系数随水深和水力坡度的增大而增大,即糙率由水深和水力坡度共同决定,拟合的经验公式为
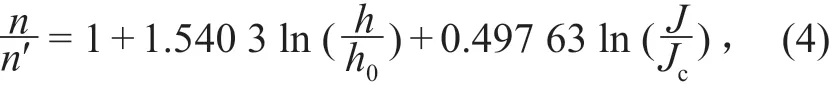
式中:n′,h0和Jc分别为均匀流时的糙率系数、正常水深和渠道坡降;n,h和J分别为非均匀流时两断面之间的平均糙率系数、中断面水深和两断面之间的平均水力坡度。
由式 (3) 和 (4) 分析可得,明渠糙率系数值的主要影响因素有R,h及J。经以上分析,在天然河道高洪水期,根据实测资料反推糙率计算过程中,相比明渠糙率系数的主要影响因素,对天然河道的糙率值影响较大的因素为:表示断面处水流所具有位能的水位Z,反映过水断面形状的水力半径R,表征能量在上下比降断面间沿程损失的水面比降S。
2 测验河段糙率值分析
莺落峡水文站系黑河干流出山口水量控制站,干流断面为黑河上游与中游的分段坐标。干流测验河段基本顺直,上狭下宽,略呈喇叭形,河床由砂砾石组成,右岸修筑有防洪墙及浆砌石护坡,左岸为沙卵石滩。基上约 600 m 处右岸有红沙河山洪注入,红沙河为季节性河流,当上游有暴雨时产生洪水,其余时间为干沟;约 1.5 km 处建有龙渠水电站五孔拦河闸;约 5.0 km 处有龙首电站拦河坝调节蓄水。测验河段上下游均由弯道控制,高水有横比降影响,中低水主流稳定。上、下比降及基本断面水尺布设于测验河段右岸,测流断面位于基上 50 m处。由于上游修建多座水电站,河道天然水流受人为影响较大。
2.1 基于实测流量测验糙率值
由于近些年莺落峡河道没有糙率的测验任务,基于样本数量多、实测数据可靠的原则,本研究选用 1983 年莺落峡水文站黑河高洪水时实测流量成果数据(该年份龙首电站还未修建,河道来水基本不受人为影响)进行糙率值的测验。流量测验采用传统的流速仪测流方法,得出中断面的流量,同步读取上下游比降水尺水位,计算出测验河段平均比降。全年糙率测验共 52 次,相对应的最低水位为 3.03 m,最高水位为 4.17 m。点绘Z-n散点图,如图 1 所示,可看出n值分布散乱,基本无规律可循。
2.2 基于 LM-BP 神经网络模型推测糙率值
2.2.1 糙率值推测原理分析
BP 神经网络是一种多层前馈网络,基本思想是学习过程由信息的正向和误差反向 2 个传播过程组成,本质上是一种高度的非线性映射[12]。通常由输入层、隐含层和输出层组成,层与层之间相互连接,每层节点之间没有任何连接,结构如图 2所示。
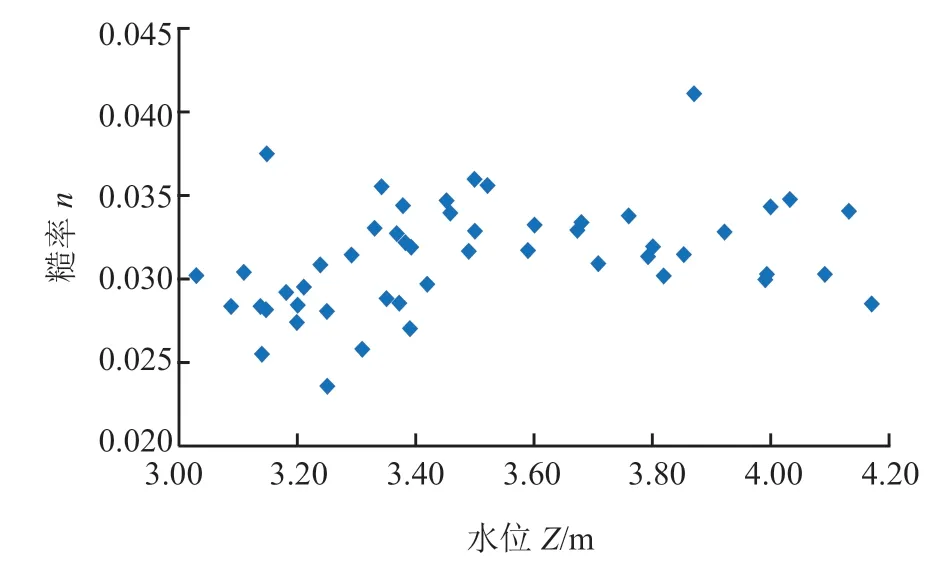
图 1 Z - n 关系
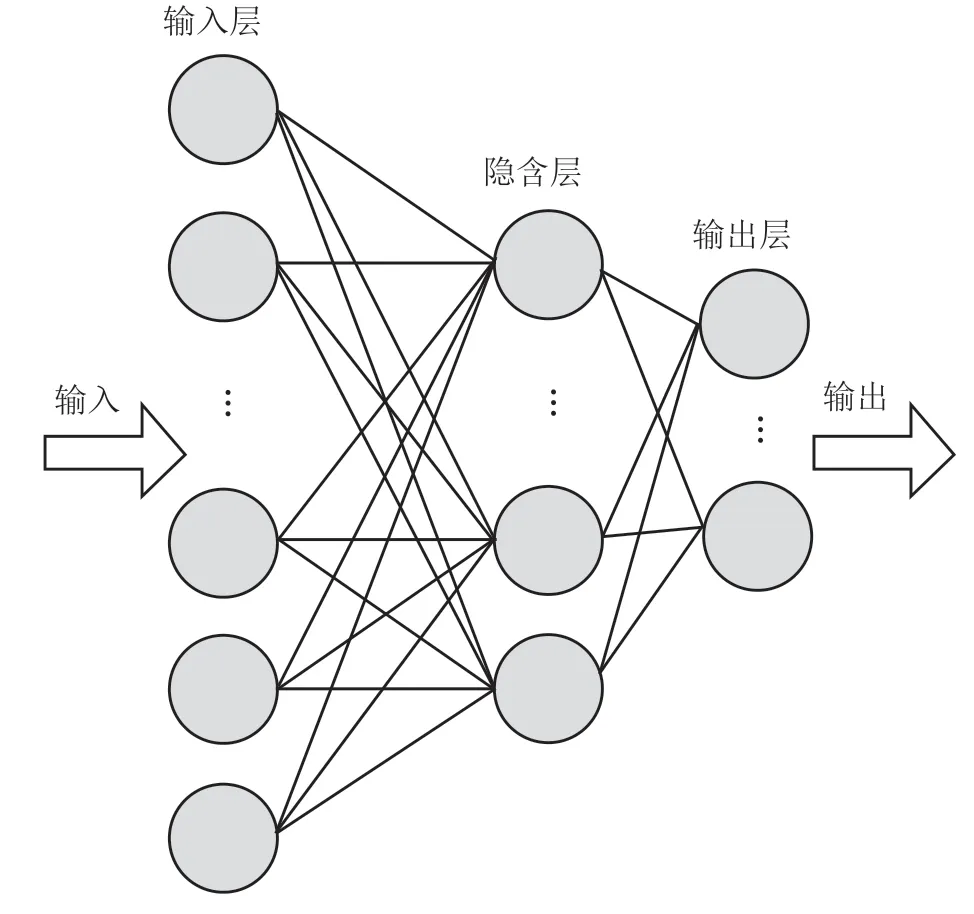
图 2 神经网络结构模型
LM 又称阻尼最小二乘法,是梯度下降和高斯-牛顿法的结合,兼具局部快速收敛和全局搜索等特性。LM 算法是基于避免计算修正速率中 Hessian 矩阵而设计的,当误差性能函数具有平方和误差形式时,Hessian 矩阵可近似表示为

式中:J是包含误差性能函数对网络权值一阶导数的雅克比矩阵;JT是J的转置矩阵;T 表示矩阵的转置。
与其他训练算法相比,LM 算法需要大量内存,更适用于训练权值和阈值数目少于几百的神经网络[13]。由于本研究设计的预测模型规模较小,因此优选 LM 算法作为 BP 神经网络预测模型的训练方法。
2.2.2 糙率值推测模型设计
在推求糙率值的 BP 神经网络模型中,输入量为水位Z,水力半径R及水面比降S,输出量为糙率n。采用经典的三层 BP 神经网络设计结构,节点数过多或过少都会影响预测模型的精度,需要试探性地寻找兼顾网络收敛速度和精度的节点数[14]。通过多次训练实验,本研究隐含层节点数设为 7,预测模型结构如图 3 所示。
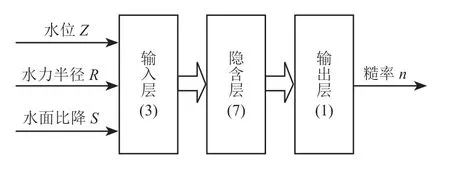
图 3 预测模型结构
应用 Matlab 2014a 软件编程进行 BP 神经网络设计和样本训练。隐含层和输出层均采用 Tansig函数,Tansig 函数输入值可取任意值,输出值在[-1,1] 间;原始数据的归一化和反归一化函数采用mapminmax 函数,该函数可将待处理数据归一化到 [-1,1] 区间内;网络的训练函数为自适应 LM 算法。网络模型的目标参数值设为 0,最大训练次数设为 200 次。
BP 神经网络在开始训练前将各层的连接权值和阈值随机初始化为 [0,1] 之间的值,因此神经网络每次训练得到的结果不一样。鉴于莺落峡河段糙率值推测模型是基于历史数据的有导师训练方式,不要求其在线实时调整权值和阈值。因此采用预测数据和原始数据对应点误差的平方和的均值,即均方差作为网络单次优化衡量指标,适当调整模型优化运行总次数,取最小均方差值训练结果所对应的模型参数作为预测模型的最优参数。本研究设定模型运行总次数为 50 次。
2.2.3 糙率值模型训练
采用 1983 年莺落峡河段糙率实测资料作为样本,总共 52 个样本,样本总体均为河道高水期的实测数据。不同水位级下的水文特征值可能来自不同分布的总体,在反推糙率值时,应考虑不同水位级糙率值的推测模型参数可能不同。本研究选取的是高水期实测数据样本,随机抽取 46 个样本作为预测模型的训练样本,剩余 6 个样本作为测试样本。经过 50 次运行,可得最优结果对应的模型训练过程收敛情况,如图 4 所示,糙率实测值n实和推测值n推回归分析如图 5 所示。
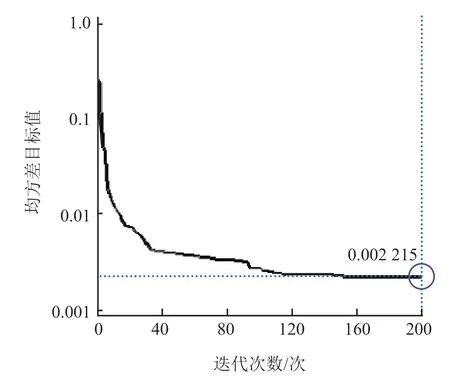
图 4 均方差目标值收敛曲线
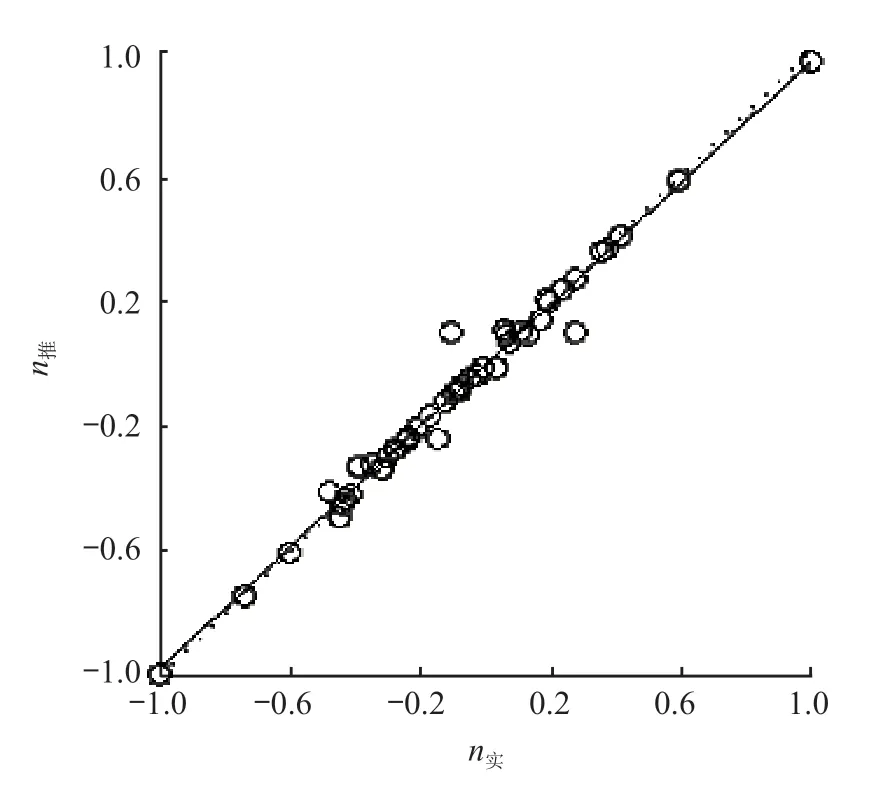
图 5 回归分析结果
图 4 分析结果:经过 200 次训练后,网络模型达到稳定的均方差目标值 0.002 215。图 5 分析结果:糙率推测值和实测值(实际糙率值归一化后的值,与实际值不同)之间的相关系数R为 0.991 01,该模型具有较好的预测性能。拟合线方程为
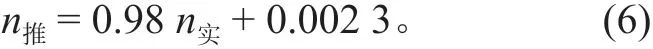
3 糙率值样本测试及分析
神经网络训练完成后,需要采用有独立样本的测试数据对网络加以检验。基于对 BP 神经网络预测模型建立和训练的分析,应用随机测试样本对确定好参数的预测模型进行测试,得到的数据对比表如表 1 所示。
BP 神经网络训练目的是找出蕴含在样本数据的输入和输出间的本质联系,从而对未经训练的输入给出合适的输出,即具备泛化能力。网络的泛化能力可通过 1 组独立的样本数据加以测试和检验。由表 1 可以得出:由测试样本数据推测的糙率值与实测值的绝对误差的绝对值最大值为 0.209 2,最小值为 0.091 0。相对文献 [15] 中应用 DHM 方法推求复式河槽综合糙率相对误差平均值为 5.629%,本研究推求的糙率值的相对误差平均值为 2.565%,因此可说明本研究训练后的模型具备一定的泛化能力。相对文献 [16] 中糙率值仅考虑流速、水力半径和河道动态参数等影响因素,本研究提出的模型不仅考虑水位、水面比降和水力半径等影响因素,还充分考虑了历史糙率值,可以更加准确地逼近真值。
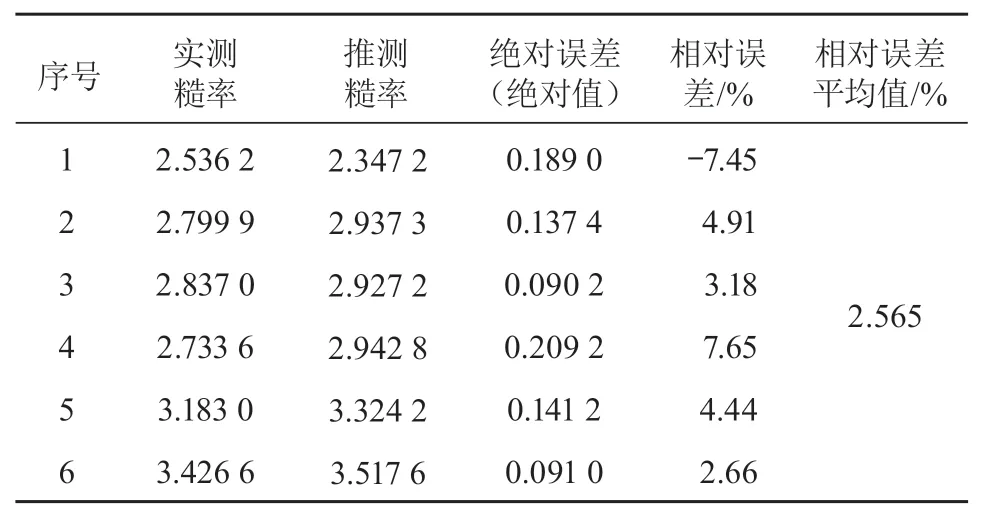
表 1 数据对比表
本研究提出的推测糙率值的方法是基于天然河道实测资料,应用曼宁公式反推的测验河段糙率值,故不适用非恒定流条件下的糙率值计算。由于天然河道在水位变幅不大的条件下,可将水流近似为恒定流,反推出的n值不只单一地表征过水断面粗糙程度的物理特性,还反映出不同水流形态对糙率值的影响。因此,反推出的糙率值是一个综合系数,且不同水位糙率值不同,可有效提高采用曼宁公式计算流量的精度。
本研究提出的方法优点在于:由水位、水力半径和水面比降可以唯一地确定一个糙率值,糙率值可以应用到河道高水期用曼宁公式推求流量的方法中,且不用对糙率值进行修正,适用于河床较稳定、比降明显的宽浅型测验河段。缺点在于:需要定期应用实测历史数据资料训练模型,进而定期更新模型的参数值,确保推测值的精度[17]。建议在实际操作过程中,参考文献 [18] 中的测流方法做比测试验,一旦超出允许误差范围,需根据最新实测资料,更新模型参数。
4 结语
本研究采用 LM-BP 算法的神经网络模型结构,利用其结构简单、可操作性强,以及能模拟任意非线性映射的特性,对莺落峡河段糙率值进行推测分析。采用莺落峡河段高水时糙率值实测资料,将影响糙率值的主要因素作为模型的输入量,糙率值作为输出量,通过网络模型的训练、测试及误差分析,表明该推求河道糙率的模型泛化能力较好。相对河网糙率反演理论计算糙率的方法,本研究提出的糙率值推求方法思路简单,精度高,但是需要历史资料作为支撑,且预测模型的隐含层节点数、学习率等参数选取灵活性大,目前没有合适的方法;在不同水位、水面比降情况下,该预测模型可以推测出不同的糙率值,可应用于曼宁公式计算流量的方法中,可提高流量测验精度。从天然河道糙率问题研究及推动水文自动化监测发展的角度而言,该方法具有一定的参考应用价值。
基于本研究遇到的问题,建议对推求糙率值的LM-BP 神经网络模型参数的确定方法,做进一步深入研究。

