有效理解算理的路径探讨

汪东兴

摘 要 算理是计算的理论依据，是计算教学中逻辑思维的运用和体现。教师要帮助学生充分理解算理，必须做到情境支撑、理情相融，操作外化、理行相随，直观呈现、理形相依，表征转化、理型相联，练习强化、理用相促。

关键词 小学数学教学 算理理解 路径探讨

众所周知，算理是计算的理论依据，是解决“为什么这样算”的客观规律，为计算提供正确的思维方式;算法是算理指导下的计算规则及逻辑顺序，是解决“怎样计算”的人为规定，它保证正确、快捷地计算。算法和算理是计算教学中相互依存的结合体，轻视算理指导、算理理解浅显的计算教学是不完整的教学。那么，计算教学中如何指导和帮助学生清晰理解算理，实现“循理入法，以理驭法”呢？笔者拟结合教学实践作简要探讨（案例所涉数学教材均为人教版）。

一、情境支撑，理情相融

现行小学数学教材，计算教学多与解决承载现实情境或背景的数学问题相伴生。此类编排，既可利用所学的数量关系列出算式，体会计算学习的现实需要，又可借助现实情境或背景，帮助学生理解并运用四则运算的含义，明晰算理，实现算理与情境的相互融合。如小数乘小数的计算（五年级上册P5例3）。

例3 给一个长2.4m、宽0.8m的长方形宣传栏刷油漆，一共需要多少千克油漆？（每平方米需要油漆0.9kg，图略）

例题教学重点是掌握小数乘小数的竖式计算方法，难点是理解小数乘小数的算理。理解算理时，教师可设计如下环节：

教学实践表明，小数乘小数的学习，学生感到困难的不是算法掌握，而是对算理的理解和表述，因此教学关键在于，教师应提供充分思考、交流的机会，帮助学生合理解释计算过程。因此教师应把引导学生分析下面的推理图，从积和因数的关系出发，完整叙述整个推理过程作为教学重心。

如此安排，既可明确小数乘小数的算理，又为后续自主归纳小数乘小数的算法做好铺垫。

二、操作外化，理行相随

操作是学生建构数学认知、形成数学能力的过程，它能使抽象的数学知识具体化，枯燥的文字叙述变成看得见、摸得着的活动，使学习过程变得有趣、快乐，富有思维内涵，有助于学生对所学知识的理解与把握。教师精心设计操作活动，让学生在活动中有所发现、有所感悟，有助于学生理解较复杂的算理。如分数除以整数的计算（六年级上册P30例1）。

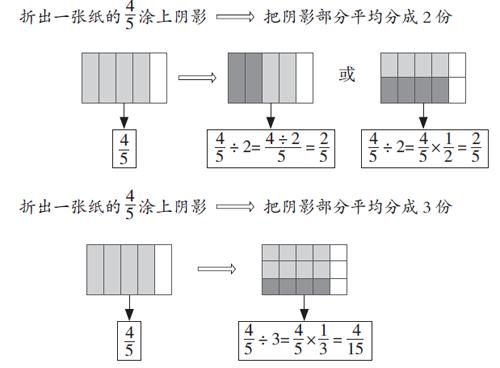
例1把一张纸的平均分成2份，每份是这张纸的几分之几？自己试着折一折，算一算。

如果把一张纸的平均分3份，每份是这张纸的几分之几？

分数除以整数的算法，是分数除法的基础，根据分数意义和操作活动沟通分数除以整数与分数乘法的联系，既是理解算理的关键，也是归纳算法的关键。教学时，教师指导学生按下面步骤动手操作：

上述操作过程，教师有意识地引导学生将“图”和“式”对照起来分析、说理，帮助学生建立图形语言和数字语言的联系，有效降低学生对分数除以整数算理的理解难度。

三、直观呈现，理形相依

小学生思维发展处于以直观形象思维为主向以抽象逻辑思维为主的过渡期，学习数学知识一般遵循具体感知→形成表象→抽象概括的规律，仍需要直观形象的支持。直观手段能使其思维在感性认识的基础上参与认知过程，及时将感性认识上升为理性认识。因此，小学数学教材的编排中大量呈现点子图、小棒、方格图、立体图、计数器等结构化直观图，借助直观把复杂数学问题变得简明形象，为帮助学生理解算理提供支撑。如被除数各位上的数都能被整除的除法（三年级上册P15例1）。

三年级平均每班种多少棵？

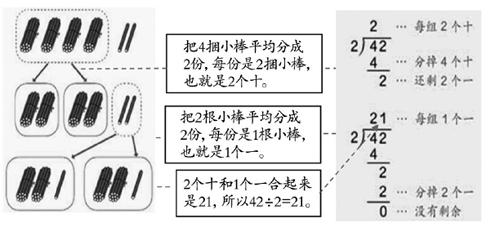
教学时，教师先引导学生观察主题图，明确解决“三年级平均每班种多少棵？”可列式42÷2计算。再借助课件直观呈现平均分及竖式计算过程，在竖式边给出每一步计算中各个数的含义，帮助学生理解算理，掌握除的顺序和竖式的写法。

上述过程中，学生能直观发现每一步分的结果与竖式中每一部分结果的位置值的对应关系，有效突破一位数除两位数的教学难点，使算理得到进一步抽象，最后达到脱离直观算理，掌握算法的预期效果。

四、表征转化，理型相联

小学生对数学知识的表征一般分为动作表征、图像表征和符号表征，学生理解算理的最终成果表现为根据题意和数量关系列出算式，用文字符号予以呈现。教学中，教师应设法帮助学生建立算理的多元表征，培养根据需要与情境在各种表征方式之间做出多元、多向联结与转化的能力，加深学生对算理的理解。如20以内的退位减法（第1课时）（一年级下册P10例1）。

教学中教师引导学生从情境中收集信息，列出算式后，借助学具感悟多种计算方法，重点通过课件直观演示、理解“破十法”算理。

最后，联系演示过程，用算式表示“破十法”的算理：

上述安排，教师把具体的操作过程和抽象的计算过程对应起来，引导学生将多种表征方式相互结合并进行有效转化，帮助学生理解算理和掌握“破十法”，也为学生脱离实物，通过思考算出得数打下了基础。

五、练习强化，理用相促

練习既是教学效果的检验工具，也是学生掌握知识、形成技能、培养能力的有效途径。计算教学中的练习，既能检测算法掌握状况、算法运用能力，又能检测算理理解程度，促进学生对数学知识的掌握和转化进程。如两位数乘两位数的笔算例1补充设计练习题：

1.想一想，填一填。

设计意图：观察思考，明确竖式每一步计算的含义，理解竖式计算算理。

2.下面计算对吗？对的画“√”，错的画“×”，说一说错在哪里并改正。

设计意图：以判断改错的形式，选取典型错例，分析说理，明确竖式每一步计算所对应的位置值，既巩固算理，又检验算法的掌握状况。

3.把下面算式补充完整。

32×3+32×40=（   ）×（   ）

11×8+11×10=（   ）×（   ）

设计意图：从逆向思考的角度，加深学生对算理的理解。

总之，算理学习对计算教学有着特殊的意义，它是计算教学中逻辑思维的运用和体现，是数学理性精神的体现，更是计算以及计算中思维方法能够灵活迁移的基础。教师要认识算理的本质，依据小学生的数学认知规律、思维特点设计教学，关注多元表征的运用和转化，有效帮助学生理解算理，从而提高计算能力。

[责任编辑：陈国庆]