三自由度弱耦合谐振式微质量测量传感器
肖奇军,罗忠辉,郭大为
(1.肇庆学院电子与电气工程学院,广东肇庆526061;2.广东技术师范大学机电工程学院,广东广州510665;3.首都医科大学附属北京世纪坛医院,北京100038)
1 引 言
近几十年来,微机电系统(Micro-electro-mechanical System,MEMS)谐振器件的研究和应用迅速增长。MEMS谐振器主要用于传感应用,通过改变MEMS谐振器的有效质量和刚度等固有物理特性,可以改变相应的谐振器的谐振频率,从而将频率偏移作为传感输出度量。例如磁力和静电力等物理力,可以通过谐振式传感器测量[1-2]。谐振器也可以应用在加速度计和陀螺仪上[3-4],其中MEMS谐振式加速度计可以获得更宽的带宽和更高的分辨率[5-8]。此外,MEMS谐振器用作加速度计时,可以增加例如基于ΣΔ调制器的静电力再平衡反馈闭环系统[9-10]。在生物和化学传感器的应用中,谐振式质量传感器近年来得到了广泛的关注。谐振器分为单自由度谐振器和多自由谐振器。单自由度谐振器结构简单,设计快速,制作方便。频移作为输出度量,单自由度谐振器的输出可以通过不同的电学设备或光学设备提取,制造成品率高,易于商品化,具有相对简单的芯片引线键合和封装。其缺点在于相对低的灵敏度,环境噪声对系统的性能影响很大,不能执行多个感应任务。多自由度耦合谐振器的优点则是提高了归一化灵敏度。它使用振动模态和模态频率来执行多目标感知或混合目标鉴别,可以采用差分电路方法抑制噪声,静电耦合可以实现系统的灵活性,适用于各种应用场合。其缺点在于器件结构设计复杂,制造成品率较低,静电耦合需要很高的直流电压,功率损耗很高。多自由度模态局部化弱耦合谐振器归一化灵敏度极高,使用特征向量偏移或振动幅值比作为输出度量,具有固有的共模抑制能力,可调静电耦合可以实现可控的系统灵敏度,但其缺点在于复杂的接口电路设计,特别是在高频器件中,受到制造误差的影响,静电耦合需要很高的直流电压。在低Q值环境下工作会极大地影响系统的性能,给生物传感带来困难。二自由度谐振式传感器在质量和刚度传感应用方面已经取得了显著的成果。与传统的以频移作为敏感输出度量的单自由度谐振器传感器相比,利用二自由度耦合谐振式传感器系统的模态局部化效应,灵敏度可以提高约2个数量级。这是因为基于周期振动系统中某一特定区域内的外部扰动能量导致了系统振型的变化。近年来,赵纯等人提出了一种利用谐振器谐振幅值比作为输出量的传感方法。这种方法可以同时实现高灵敏度和良好的共模抑制。他们提出了一种三自由度弱耦合谐振器系统,该系统利用模态局部化,在真空环境下工作时,与传统单自由度MEMS谐振器相比,其刚度变化灵敏度提高了近3个数量级[11]。在相同的刚度扰动情况下,谐振器幅值比的变化明显大于谐振器频移的变化,表明谐振器幅值比是一个对外界扰动敏感性较高的输出度量[12]。本文以三自由度耦合谐振器芯片作为质量传感器,研究了微质量测量原理及其实现方法。该方法能通过检测电压幅值比变化实现对微小质量的检测。本文首次将3-DOF模态局域化耦合谐振器用于在空气中进行微质量测量,并进行了系统仿真与实验,同时也是首次在理论上完成对混合质量测量的建模。
2 三自由度模态局部化耦合谐振器设计
2.1 工作原理
三自由度模态局部化耦合谐振器可以用质量-弹簧-阻尼器系统来表示。图1说明了三自由度耦合谐振器的工作原理。如果谐振器3受到外部质量的扰动,并假设没有外力,那么三自由度耦合谐振器系统在时域中的运动方程可以表示为:
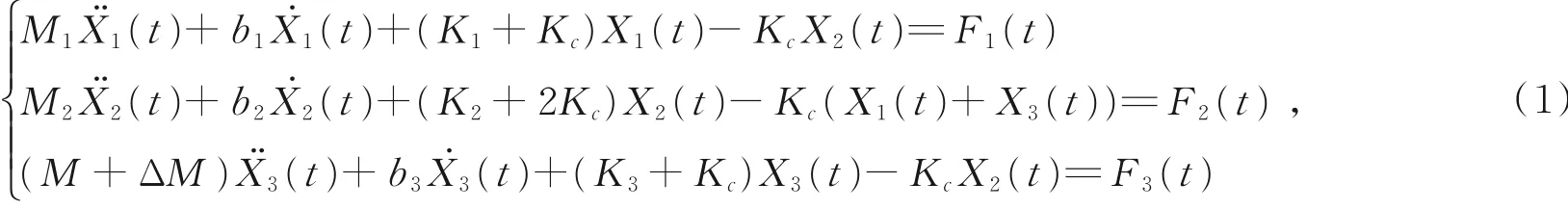
式中:M1,M2和M3分别对应于谐振器1、谐振器2和谐振器3的有效质量,K1,K2和K3代表各谐振器的有效刚度,ΔM代表质量扰动,Kc代表耦合刚度,b1,b2和b3分别代表耦合系统中的阻尼系数,X1,X2和X3代表各谐振器的位移,F1,F2,F3分别为施加在谐振器1、谐振器2和谐振器3的外力。
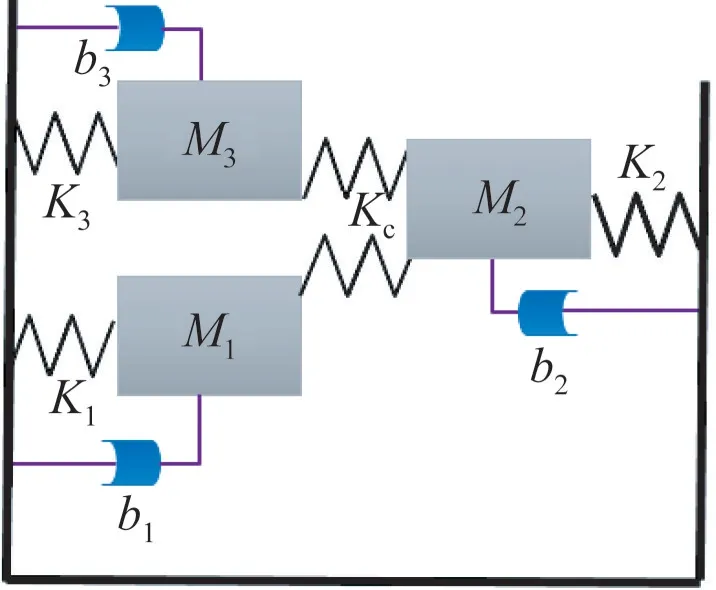
图1 三自由度耦合谐振器系统的弹簧-质量-阻尼模型Fig.1 Spring-mass-damper model of 3-DOF coupled resonator system
为了使谐振器1和谐振器3的位移最大化,提高信噪比,设计了三自由度耦合系统中的中间谐振器,其刚度至少是相邻谐振器刚度的两倍。另一方面,为了实现对多质量扰动的测量。在结构方面,对原有的三自由度耦合谐振器进行了一些调整,使用了3个刚度相同的谐振器,同时对3个振子中的两个振子施加外部质量扰动。三自由度谐振器的系统方程可以用矩阵形式重写,对特征矩阵进行求解,所得的特征值和特征向量分别对应共振频率及相应振动模态下的振幅。假设M1=M2=M3=M,K1=K2=K3=K,ΔM1和ΔM2分别为施加在M1和M2上的扰动质量,多质量扰动下的特征矩阵可以表示为:
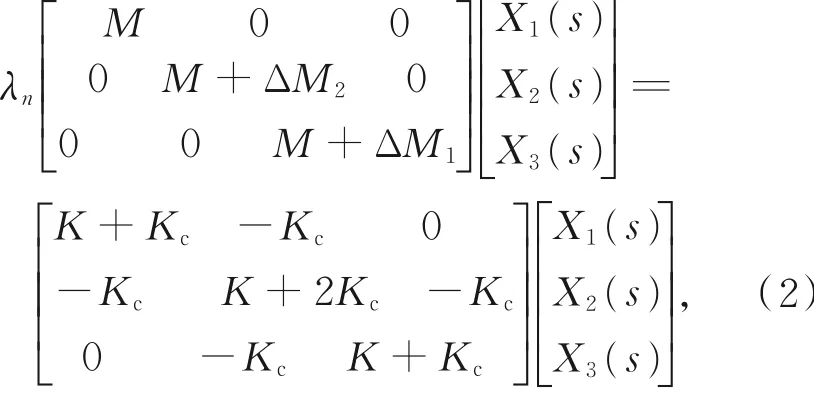
式中:特征值λn=-ωn2代表每个振动模态的相应模态频率,同时振动幅值和特征向量相关。
在谐振器3上加入质量扰动的同相和反相模态频率,分别为:
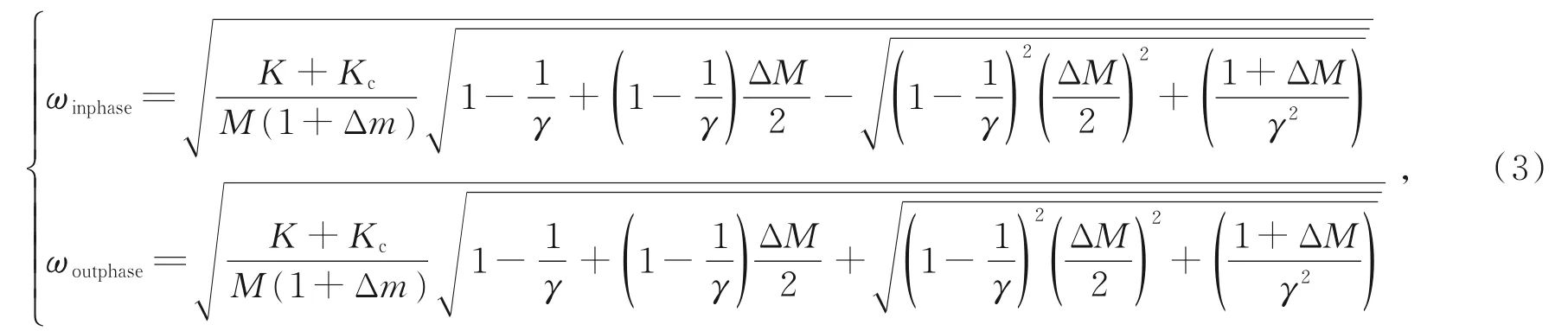
2.2 三自由度模态局部化耦合谐振器设计和制造
三自由度谐振器芯片的布局如图2所示。三自由度谐振器由3个平衡质量及其支承梁组成。两个驱动电极分别放置在装置的两侧。通过集成在谐振器1和谐振器3上的差分梳齿电容,产生运动电流形式的传感信号。差分电容检测技术可以有效地抑制共模信号。3个质量块通过外部直流电源静电耦合。与固体-机械耦合元件相比,静电耦合可以达到可调耦合的效果,以及相对较弱的耦合强度。直流耦合电压可以通过与谐振器1和谐振器3连接的锚点施加。中间的谐振器2接地。
所制造装置的尺寸参数如下:结构厚度为30μm,支承梁长度和宽度分别为350μm和5 μm,中梁宽度为7.5μm,梳齿重叠长度为70μm,质量块长度为360μm,质量块之间的间隙和梳齿之间的间隙为4.5μm。利用硅绝缘体(SOI)工艺制作了三自由度谐振器。工艺流程采用深反应离子刻蚀(DRIE)形成器件结构。对于最终释放的悬挂部分,如质量块和悬臂梁,采用HF酸湿法释放技术。
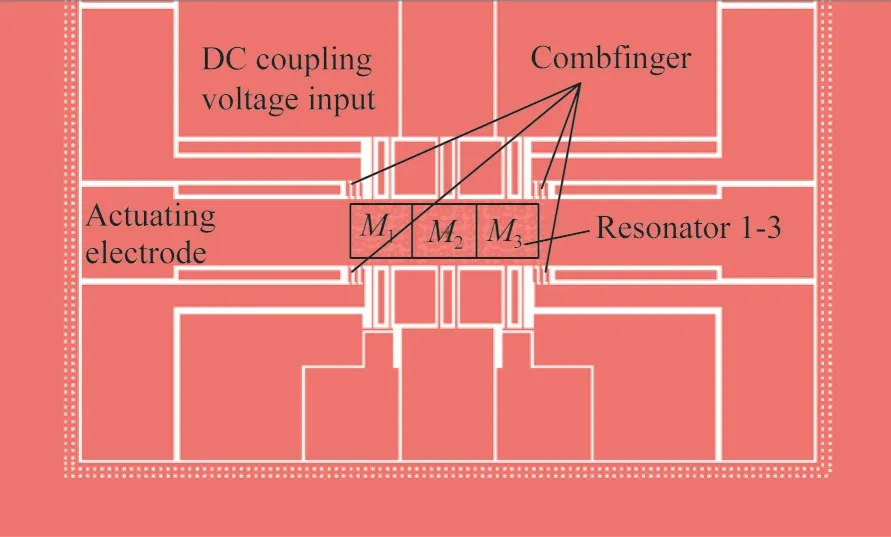
图2 三自由度谐振器的布局Fig.2 Layout of 3-DOF resonator
2.3 三自由度模态局部化耦合谐振器检测
检测线路如图3所示,函数信号发生器(SIGLENT SDG 2122X)产生高频交流信号使谐振器振动,使电容式感应梳齿的电容产生变化,由低噪声,FET输入运算放大器OPA657U组成的前置放大器将从梳齿采集到的微弱电流信号放大后转换成电压信号,再经过AD8429仪用放大器差分放大后接入锁相放大器(Anfatec elockin204/2),进行频率响应分析。静电耦合由外接直流电源实现,为减小电路噪声,将谐振器和电子元器件集成在同一块线路板上。
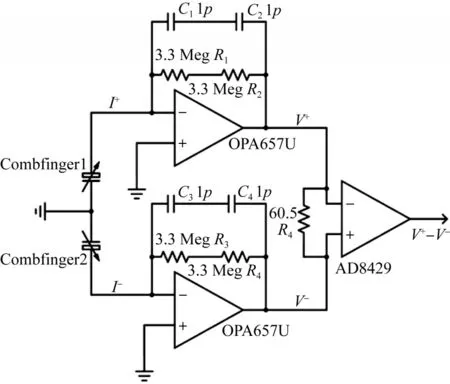
图3 三自由度谐振器的接口电路Fig.3 Interface circuit of 3-DOF resonator
3 仿真和实验结果分析
3.1 仿真结果分析
根据理论方程式(1)进行仿真,结果如图4(a)所示,可以清楚地观察到同相模态和反相模态频率特征与轨迹转向随相对质量扰动的变化。幅值比变化相对质量的扰动如图4(b)所示。
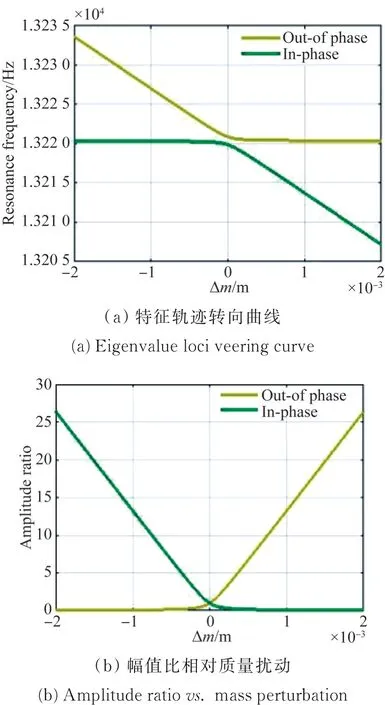
图4 响应质量扰动的三自由度局部化弱耦合静电谐振器Fig.4 Response of 3-DoF mode localized weak coupled resonator to mass perturbations
对振幅变化量,幅值比变化量和谐振频率变化量3个输出指标进行比较。用式(4)计算幅值比变化AR,振幅变化AC和谐振频率FS变化的归一化灵敏度sAR,sAC和sFS。其中AR0,A0,F0和M分别为未施加扰动时的幅值比、振幅、谐振频率和质量,ΔM为质量扰动,在三自由度弱耦合谐振器系统中,幅值比变化与振幅变化和谐振频率变化相比具有最高的归一化灵敏度,如图5所示,横纵坐标为幅值比、振幅和谐振频率的变化量与未加扰动前的值之比。
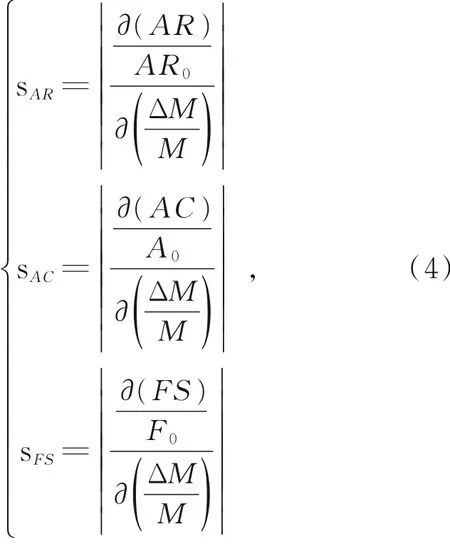
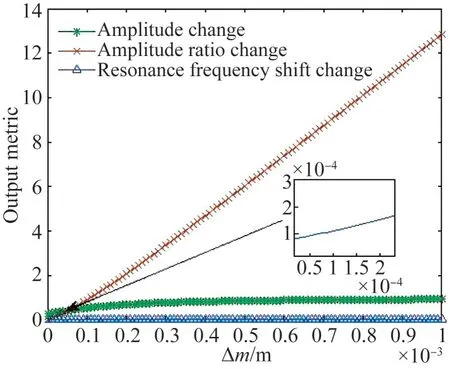
图5 三自由度弱耦合谐振器在三种不同输出指标下的归一化灵敏度Fig.5 Normalized sensitivity of 3-DOF weakly coupled resonator in terms of three different output metrics
通过引入静电驱动力和大气压下的阻尼系数,根据式(1)建立了MATLAB/SIMULINK仿真模型,如图6所示。该模型主要包括激励部分、谐振器部分和电容传感部分,还包括接口电路元件,如放大电路和电子元件的相对热噪声。为了获得更真实的三自由度分析系统的特性,在方程中忽略了阻尼项。模拟计算了耦合谐振器系统受到多质量扰动时,三自由度谐振器系统的响应,其目的是预测三自由度谐振器在多质量扰动下的工作性能。图7(a)和7(b)分别为谐振器1和谐振器3的频率响应,其中谐振器2被施加从20 ng到100 ng,以20 ng递增的质量扰动;谐振器3被施加从10 ng到50 ng,以10 ng递增的质量扰动。
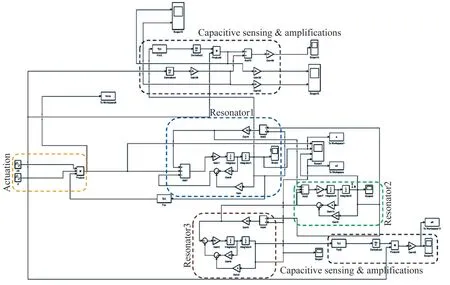
图6 MATLAB/SIMULINK仿真模型Fig.6 MATLAB/SIMULINK simulation model
3.2 实验结果分析
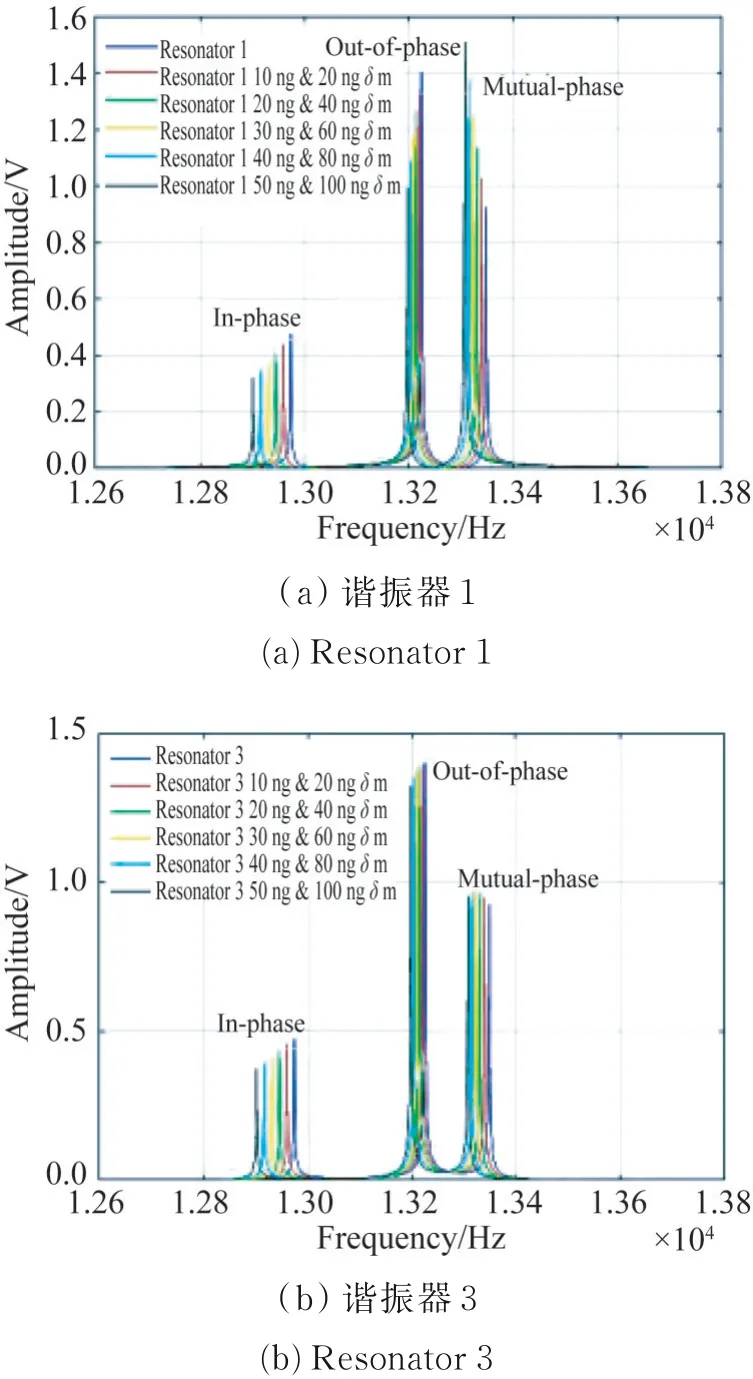
图7 频率响应和多质量扰动之间的关系Fig.7 Relationship of frequency responses with multi given mass perturbations in MATLAB/SIMULINK simulation
实验采用磁性纳米颗粒作为质量扰动实验,因为它们成本低,易于操作,而且去除方法简单。在谐振器1上加入直径为10μm、浓度为5 mg/mL的磁性纳米粒子溶液,通过控制溶液浓度来控制附加质量。通过对谐振器1施加质量微扰进行3自由度耦合谐振器芯片测试,并用接口电路测量了谐振器1和谐振器3的振幅,相应的系统频率响应由锁相放大器捕获。利用质量扰动前获得的数据对谐振频率偏移、振幅变化和谐振幅值比进行了标定。图8(a)和8(b)分别显示了三自由度耦合谐振系统在3种质量扰动下的谐振器1和谐振器3的频率响应。连续3次的添加量分别为180,85和125 ng。
图9 给出了添加质量扰动前后谐振频移、振幅和谐振幅值比的变化率随归一化质量扰动的变化。其中,振幅变化是谐振器振幅与未受干扰谐振频率下的振幅的偏差,而幅值比是谐振器1和3的振幅之比。可以看出,电压幅值比变化产生的归一化灵敏度大约是振幅变化的4倍,大约是频移变化的两个数量级。根据实验数据,频率改变作为灵敏度的误差为7.3%,振幅改变作为灵敏度的误差为12.1%,幅值比改变作为灵敏度的误差为67.3%。实验结果和仿真结果的谐振幅值比作为灵敏度相差大的主要原因在于:加工误差造成的振子结构不对称,以及在空气中进行质量检测所造成的大阻尼系数引起的系统性能下降。测量不确定因素为空气中的大阻尼系数,加工误差以及信号采集电路中的噪声。
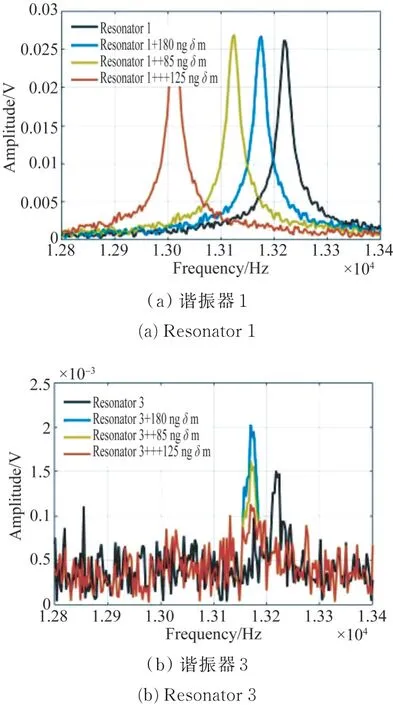
图8 三自由度耦合谐振系统的频率响应实验结果Fig.8 Frequency response of 3-DOF weakly coupled resonator
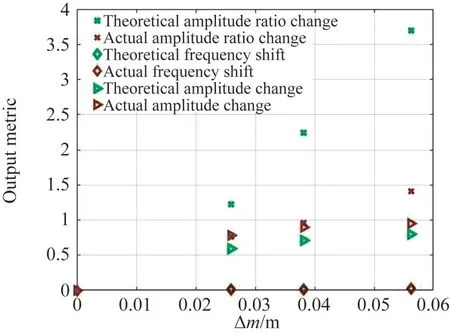
图9 理论和实验灵敏度Fig.9 Theoretical and experimental sensitivity diagram
根据提取的实验数据,考虑空气阻尼引起的机械噪声、相位噪声、接口电路引起的热噪声和环境噪声构成的总噪声。通过在MATLAB仿真模型中引入真实的总噪声值,可以提取出质量传感器系统的噪声,并得出最大分辨率。采用这种方法,在大气压下工作的三自由度模态局部化谐振器的最小可检测质量值为2 ng。
4 结 论
本文研究了基于三自由度模态局部化弱耦合谐振式微质量传感器的工作原理及仿真模型,并给出了设计、制造和检测方案。仿真结果表明,幅值比的变化趋势可以用来确定在谐振器上是否存在质量扰动,幅值比变化值可以用来计算谐振器上附加的质量扰动量。实验结果表明,电压幅值比变化产生的归一化灵敏度为21.7,电压振幅变化的归一化灵敏度为5.4,共振频移变化的归一化灵敏度为0.09,检测的最小质量为2 ng。因此,该三自由度耦合谐振器可以作为质量测量传感器,其成功研制是朝着开发生物传感器迈出的重要一步。这种传感器不仅可以利用模态局域化耦合谐振器的优点,而且还可以进行混合样品质量测量。

