一类具有时滞的随机SISV 传染病模型的稳定性

周艳丽, 任同擎, 陈立范, 王宏杰

（上海健康医学院 文理教学部，上海 201318）

1 问题的提出

随机延迟微分方程是Itô和Nisio 在1964 年引入的，在过去的几十年受到了不少学者的关注并取得了一定的成果[1-4]。文献[5]研究了具有时滞的随机SIR（susceptible, infective and removed）传染病模型，通过构造李雅普诺夫函数得到了无病平衡点和地方病平衡点的渐近性态。文献[6]在采用部分保护性接种疫苗的情况下，得到了随机SIS（susceptible, infective and susceptible）传染病模型的阈值。文献[7]研究了具有饱和发生率的随机SIR和SEIR（susceptible, exposed, infective and removed）传染病模型，得到了模型的阈值，并根据阈值分析了模型的动态传播行为。文献[8]研究了一类具有随机效应的SIRI（susceptible, infective, removed and infective）传染病模型，讨论了随机模型的解在相应确定性模型的平衡点附近的震荡行为以及随机模型的解的持续存在和疾病灭绝的充分条件。

考虑到疾病的发生和发展会受到接种时滞和环境等随机因素的影响，本文建立了一类含确定免疫期时滞的随机SISV（susceptible, infective,susceptible and vaccinated）传染病模型，并通过对该随机模型的研究来揭示时滞和环境随机因素等对疾病传播的动力学影响。由于疾病流行途径和方式的复杂性，在以上文献的基础上，考虑了更为一般的非线性发生率形式： βS f(I) ， 其中， β表示易感者和感染者之间的传染率，S表示易感者，函数f(I)∈C2满足以下性质[9]：

显然，f(I)在 [0, +∞)上是Lipschitz 连续且对所有的I>0， 有 0 ＜f(I)≤f′(0)I成立。

2 模 型

设S(t),I(t),V(t)分 别表示t时刻易感者、染病者与已接种的人数，N(t)表 示t时刻的总人口数，假设没接种者都是易感者，A表示人口常数输入率，A>0；q表示接种者的比例， 0 ≤q≤1；p表示易感者被接种率，p≥0 ；d表示自然死亡率，d>0；γ表示疾病恢复率， γ>0； β表示易感者和感染者之间的传染率， β>0； τ 表 示接种免疫期， τ ≥0。文献[10]考虑确定性传染病模型

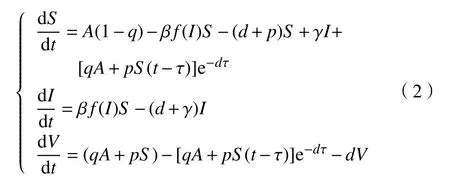
当R0≤1， 模型（2）有唯一的无病平衡点E0=(S0,I0,V0)，且全局渐近稳定。

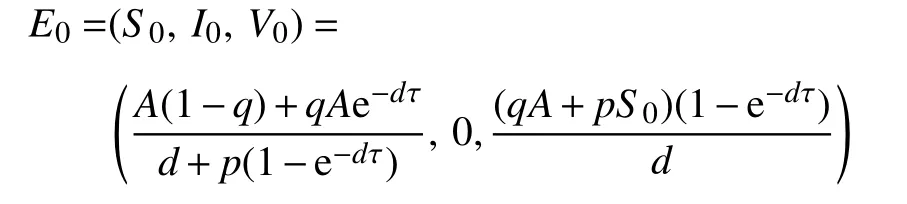
当R0>1，模型（2）则存在唯一的正平衡点（地方 病 平衡 点），且全 局 渐近 稳定，

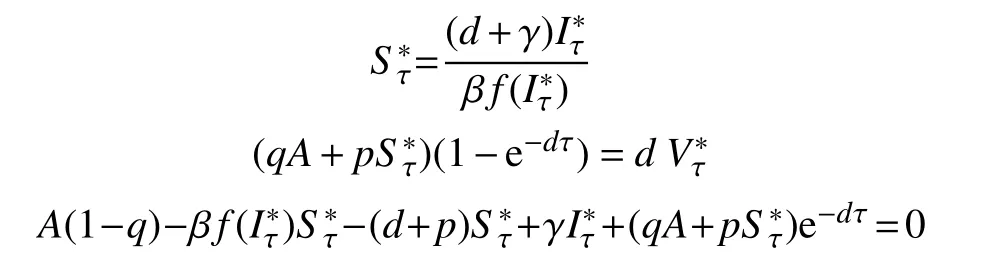
本文将在以上研究的基础上考虑一类具有接种时滞的随机传染病模型

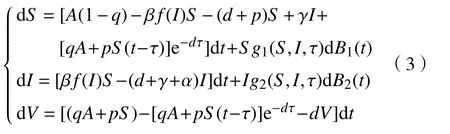
其中，g1,g2∈C2，且满足=0,B1(t),B2(t)为 定义在完备的概率空间(Ω,{Ft}t≥0,P)上的相互独立的标准布朗运动， {Ft}t≥0是 Ω上的一个 σ代数且满足通常条件（即右连续，F0包含所有零测集），函数f(I)满 足式（1）中的条件， α ≥0，α表示疾病额外死亡率。

由于模型（3）的前2 个方程不受第3 个方程的影响，不影响结论的一般性，仅考虑如下模型：

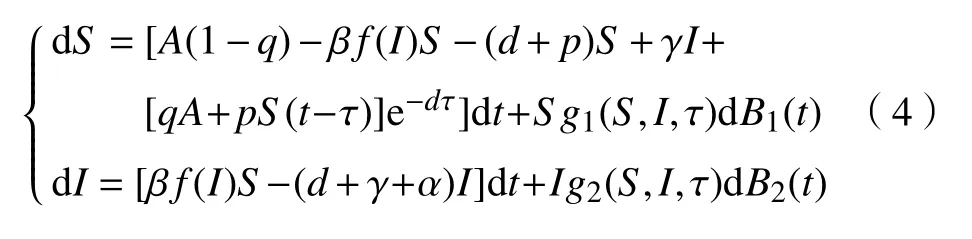
3 模型的全局正解存在唯一性

定理1假设模型（4）的初始条件为：S(θ,ω)=φ1(θ), φ1(0)>0和I(0,ω)=φ2(0)>0，且系统的解满足S(θ,ω)=φ1(θ)∈C([-τ,0],R+)。 对所有t≥0，模型（4）依概率1 存在唯一的正解 (S(t,ω),I(t,ω))，即对所有t≥0，S(t,ω)>0,I(t,ω)>0，几乎必然成立。此外，对所有t≥0，有下式成立：

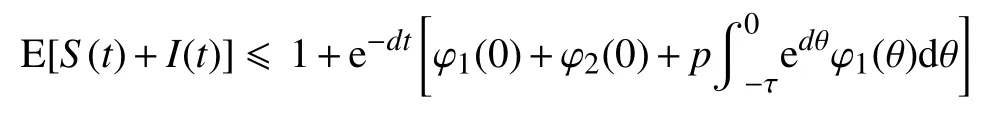
证明由生物意义可知，S(t)>0,I(t)>0。现证明随机模型（4）对于任意给定的初值都有唯一的全局正解（即在有限时间内不会爆破），此时要求系统的系数满足线性增长条件和局部Lipschitz 条件，即对任意初始值 φ1(θ)，φ2(θ)，θ ∈[-τ,0]，且φi(θ)∈C([-τ,0],R)，i=1,2，模型（4）存在唯一的1 个局部解(S(t,ω),I(t,ω))，t∈[-τ,τe(ω))， 其中，τe(ω)为爆破时间[10]。但是，模型（4）的系数不满足线性增长条件，故模型（4）的解在有限时间内有可能爆破。

记φi(θ)∈C([-τ,0],R+), φi(0)>0,i=1,2。首先，证明S(t),I(t)在t∈(0,τe(ω))上几乎必然为正。

定义停时：

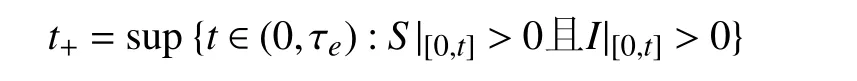
现证明t+=τe，几乎必然成立。为此，假设P{t+＜τe}>0。定义函数

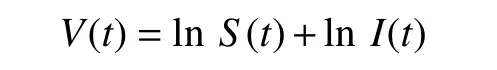
对几乎所有ω ∈{t+＜τe}和t∈[0,t+)，利用Itô公式，有

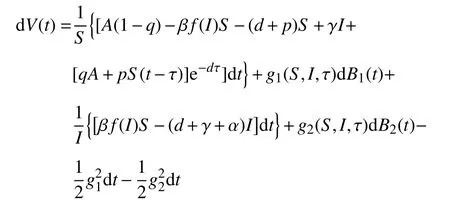
整理可得

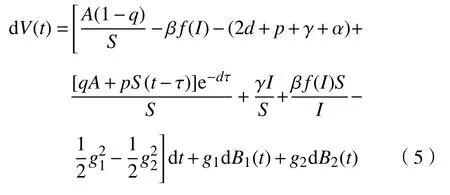
对式（5）两边从0～t积分，可得

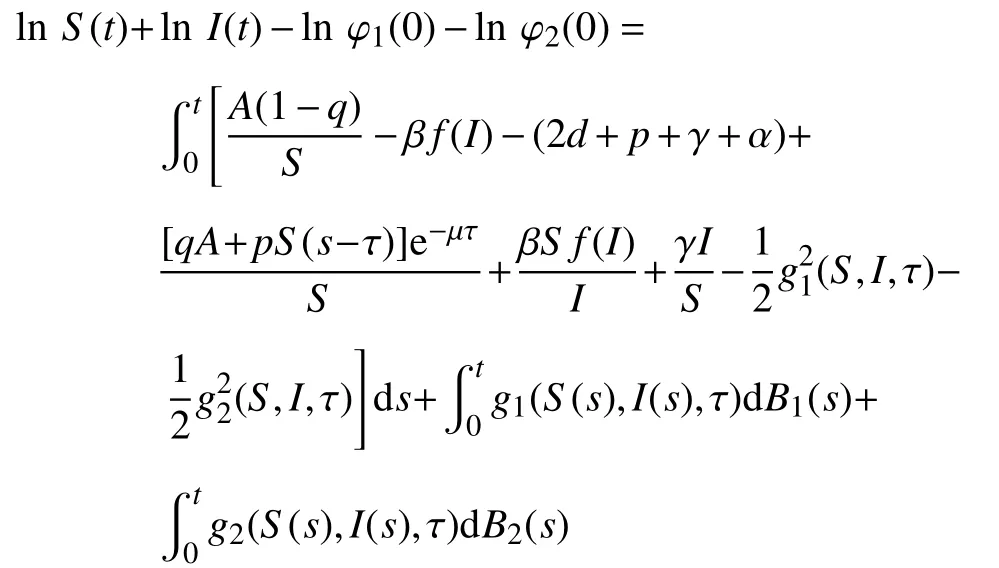
由于S,I均为非负，故下面不等式成立：

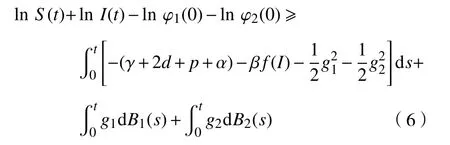
显然，几乎对所有的 ω ∈{t+＜τe}， 都有S(t)>0,I(t)>0 在t∈[0,t+)上 成立，且S(t+)I(t+)=0。所以，

由式（6）可得

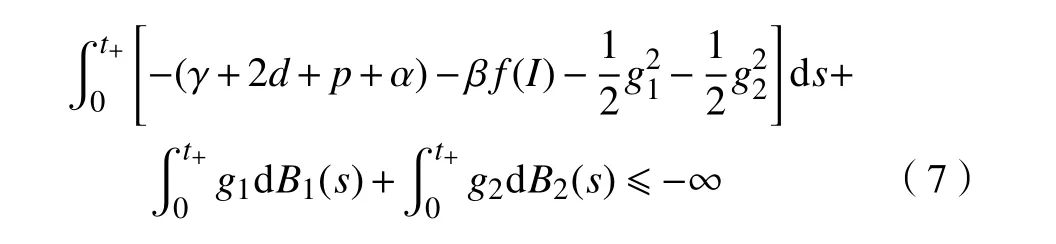
由于连续函数在有限闭区间上的积分是有限的，故式（7）左端是有限的，这与式（6）左端的结论相矛盾。所以，必有t+=τe，几乎必然成立。

定义停时：

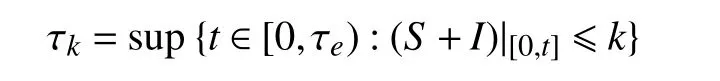
且使得任意整数k≥φ1(0)+φ2(0)。 显然，当k→∞时， τk是递增的。记则 τ∞≤τe，几乎必然成立。现利用反证法来证明P{τ∞≠τe}=0

假设P{τ∞＜τe}>0。由Itô公式，几乎对所有ω ∈{τ∞＜τe}和 所有整数k≥φ1(0)+φ2(0)，有

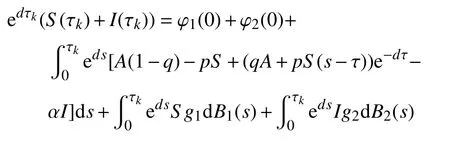
容易得到，S(τk)+I(τk)=k， 几乎必然成立。令k→∞，有

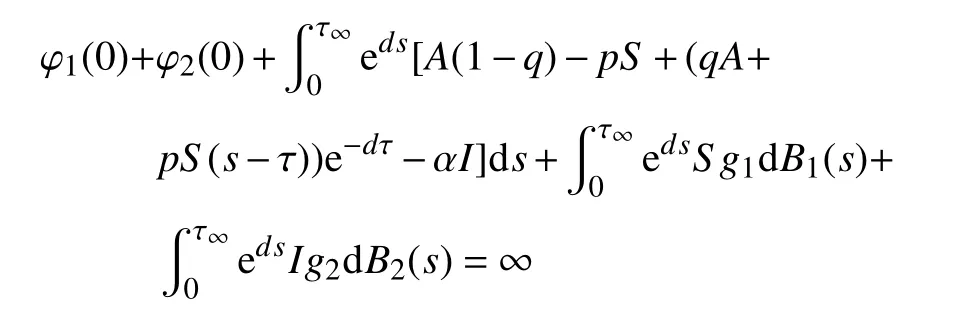
显然，上式左端是有限值，故产生矛盾，假设不成立。从而可得， τe=τ∞，几乎必然成立。

现证明P{τe＜∞,τ∞＜∞}=0。 取任意实数T>0，利用公式可得

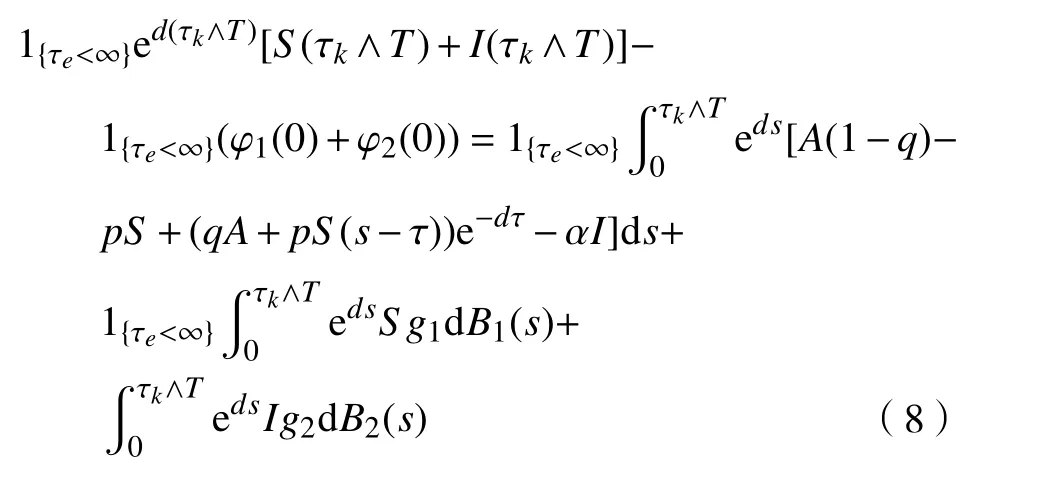
其中，1{·}是角标集合的示性函数。对式（8）两端求期望，可得

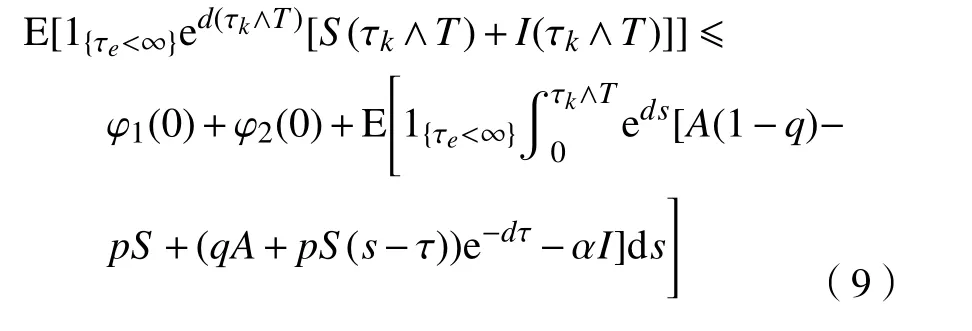
显然，

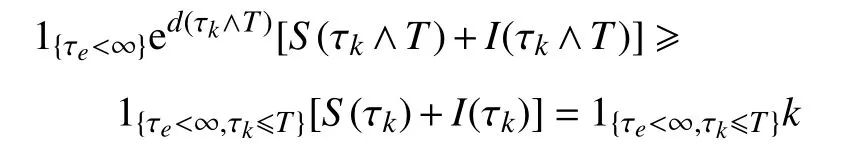
故可得

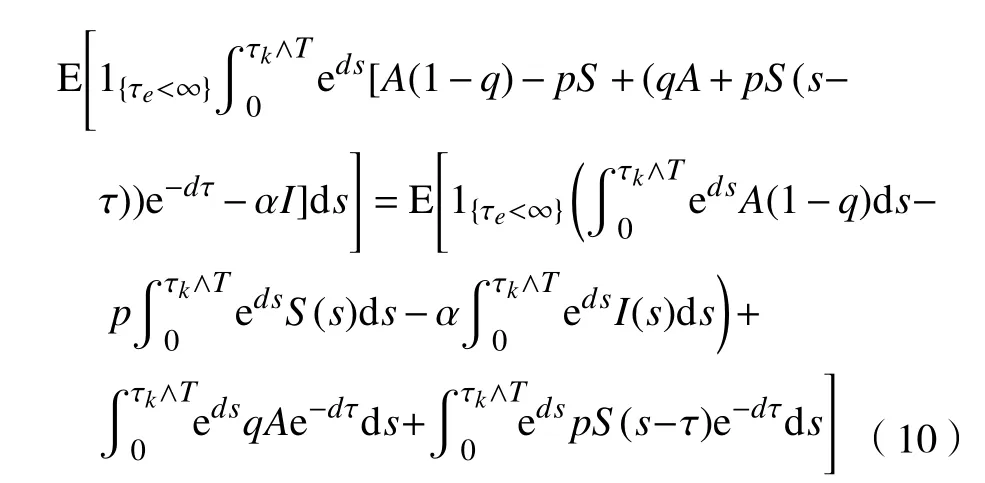
其中，

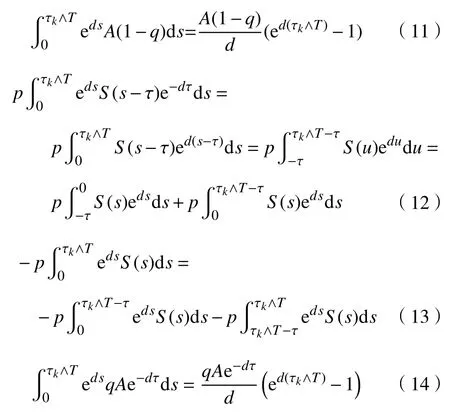
联立式（10）～（14），可得

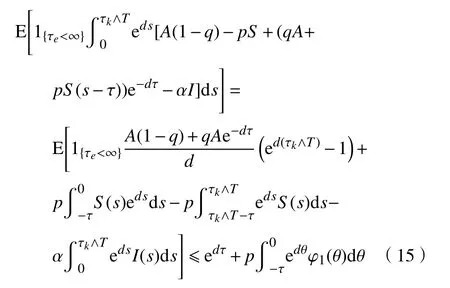
联立式（9）和式（15），可得

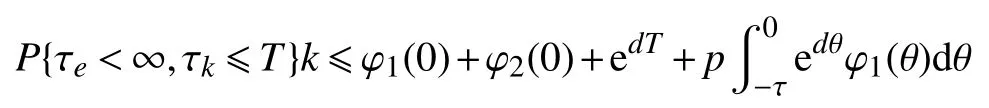
对任意的T>0 ，有P{τe＜∞,τ∞＜∞}=0。由于，

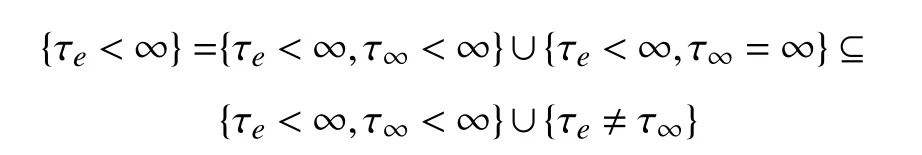
所以，P{τe＜∞}=0 。故可得P{τe=∞}=1， 即τe=∞，几乎必然成立。

当t≥0时，利用类似方法可推得

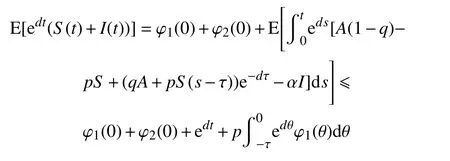
即

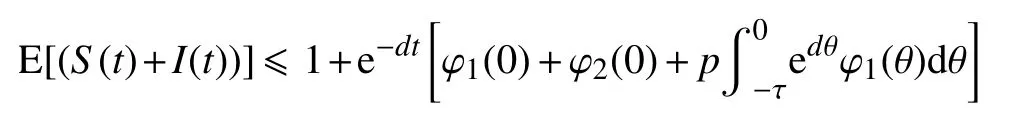
4 模型（4）线性化和解的均方指数稳定性

现讨论随机模型（4）地方病平衡点处所对应线性系统的稳定性，并分别讨论时滞为零和时滞不为零这两种情况。

由于函数f(I)满 足式（1）中的条件，所以，f(I)可以写为

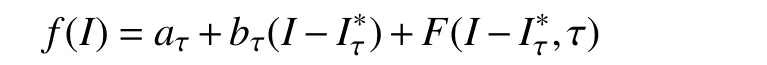
其中，F表示的次数大于等于2 的部分，且满足

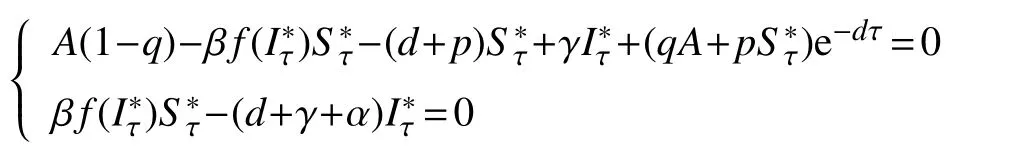
或

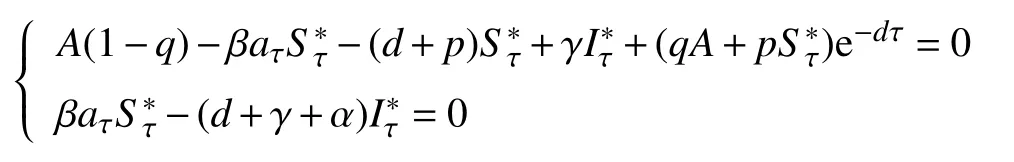
对模型（4）在正平衡点处作如下坐标变换：

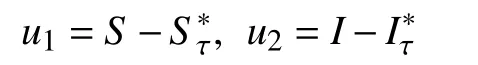
模型（4）中的g1(S,I,τ)和g2(S,I,τ)可以化为

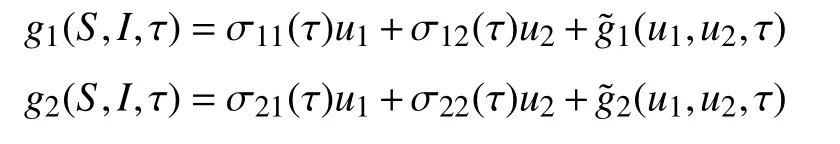
结合以上所讨论的内容，则模型（4）可化为如下形式：

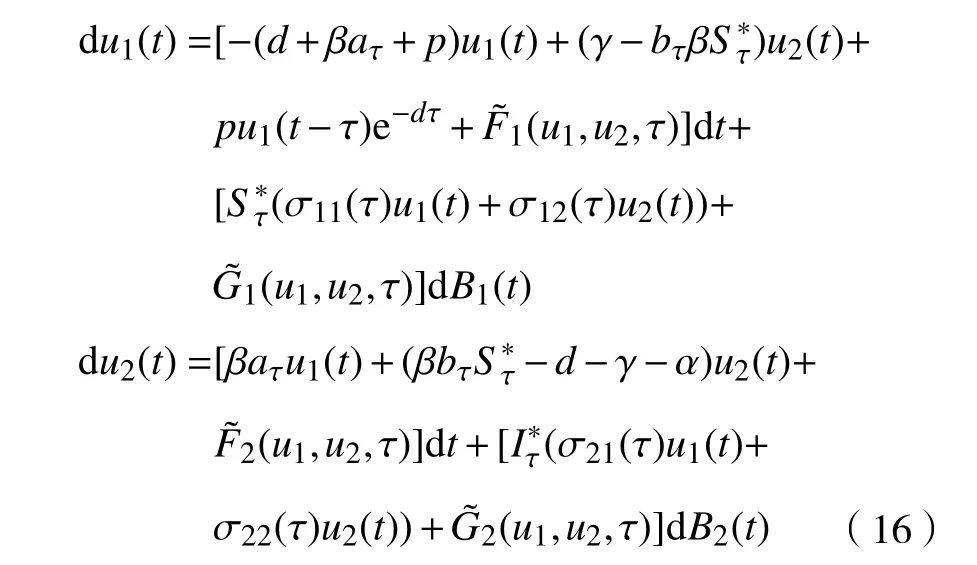
与模型（16）对应的线性部分

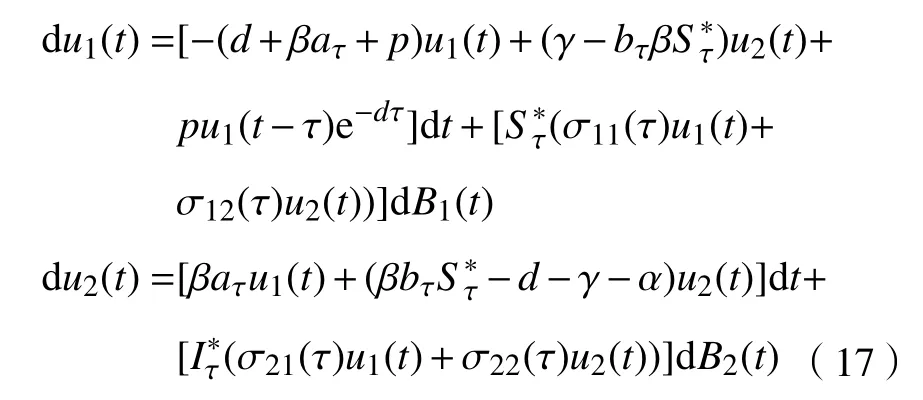
以及时滞 τ =0 时所对应的线性部分

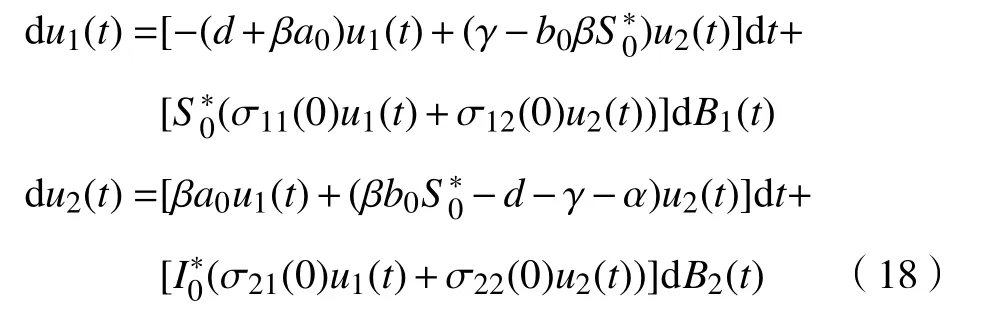
在讨论模型（17）和模型（18）的稳定性之前，先给出引理1。

引理1定义：

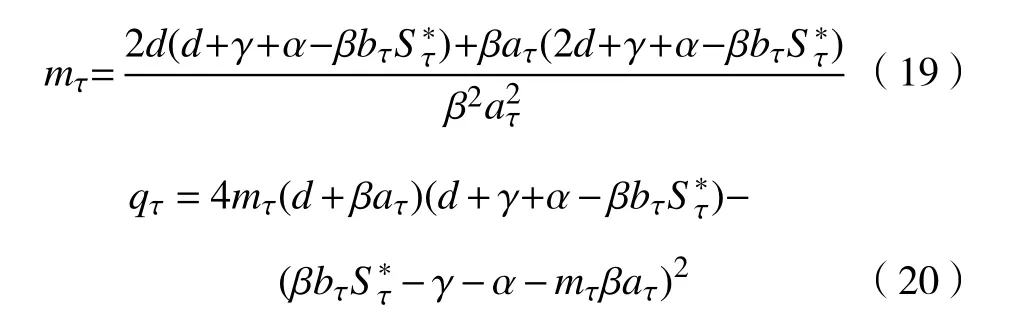
则有

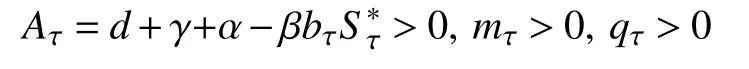
证 明由和bτ的 定 义可知，

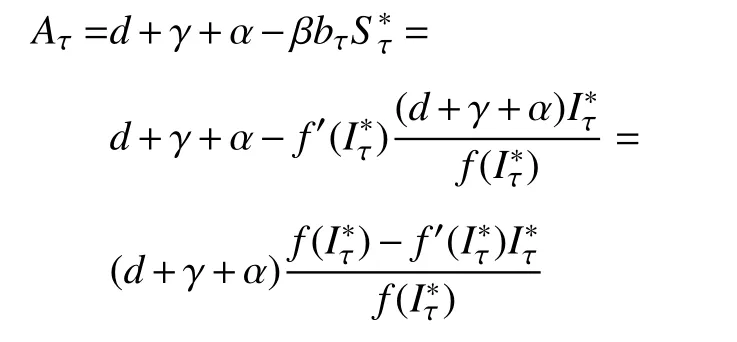
利用拉格朗日中值定理可得

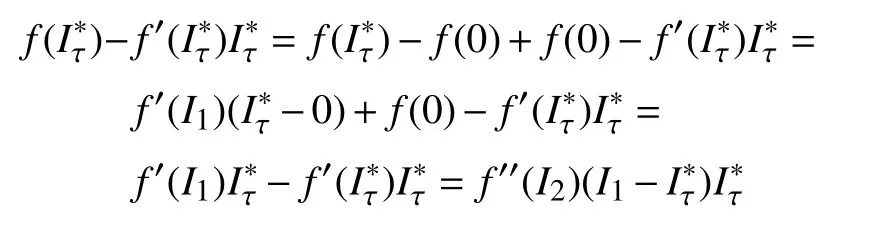
对qτ进行化简：

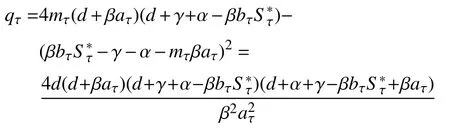
显然，qτ也为正值。

首先，讨论时滞 τ=0 时，模型（18）的平凡解均方指数稳定。

定理2保持前面所提到的假设和符号不变。如果条件

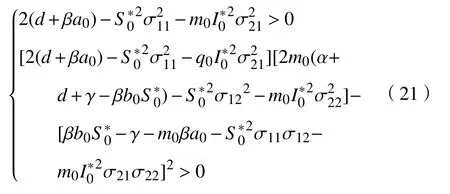
成立，则模型（18）的平凡解均方指数稳定，记σij=σi j(0),i,j=1,2。

证明定义一个C2函数V:R2→R+，

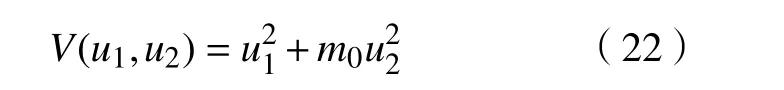
其中，

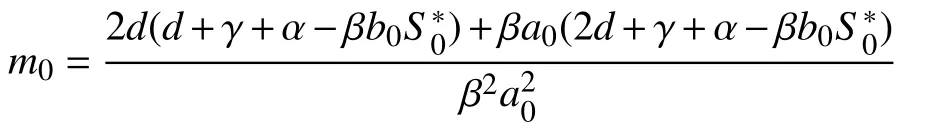
显然，V(u1,u2)正定，由Itô公式可得

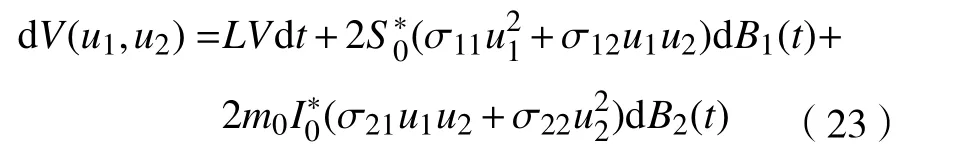
其中，

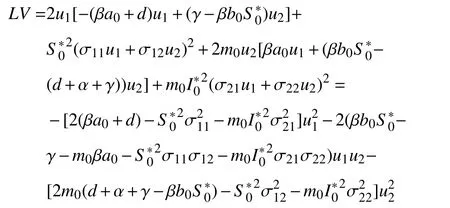
定义：

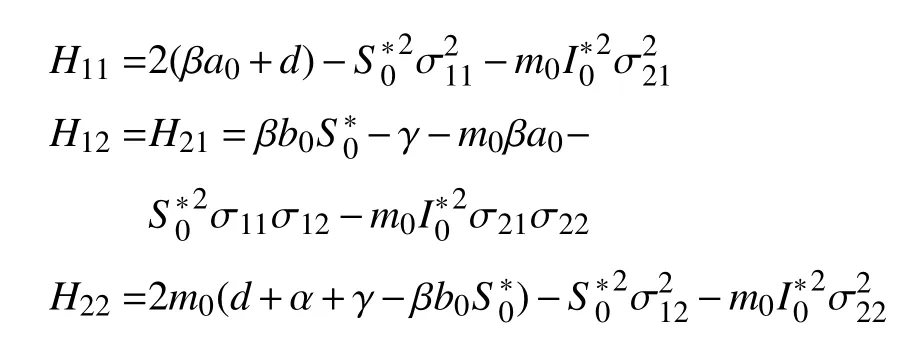
于是

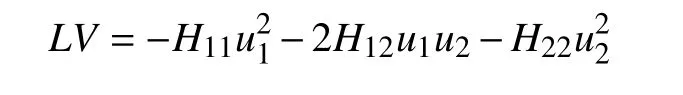
显然，由条件式（21）可知下面2 个矩阵：

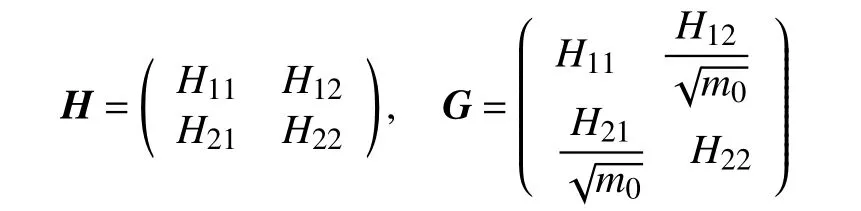
均是正定矩阵，且

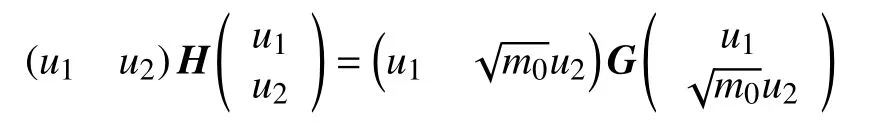
因此，对所有的 (u1,u2)∈R2满足下列关系：

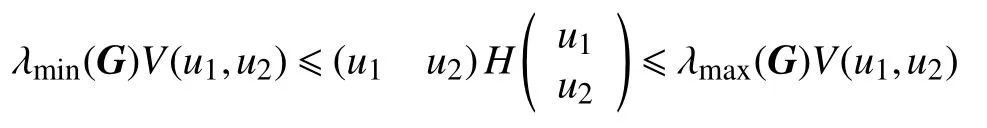
其中， λmin(G),λmax(G)分别表示矩阵G的最小和最大特征值。

令ν1=λmin(G)，则

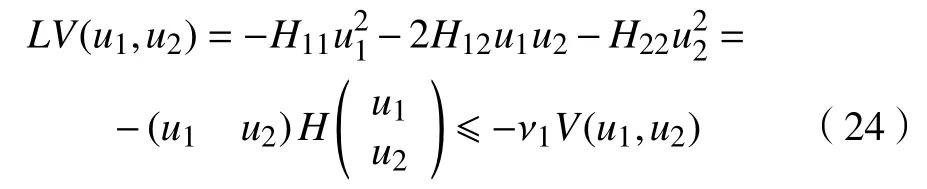
结合式（23）和式（24）并积分，可得

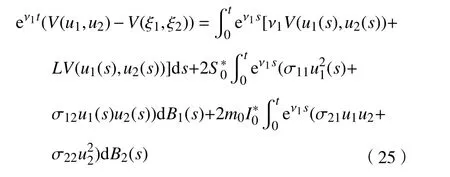
对式（25）两端取期望并结合式（24），可得

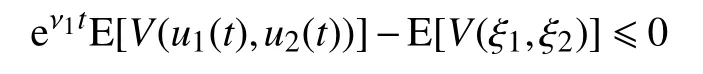
即

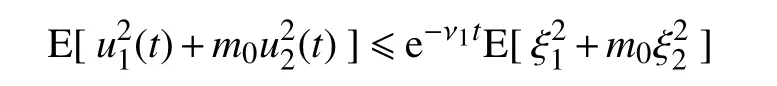
故模型（18）的平凡解是均方指数稳定的。

现讨论含有时滞（即时滞 τ ≠0）时线性系统（17）的稳定性。

为了方便起见，首先给出一些符号的定义，记定义：

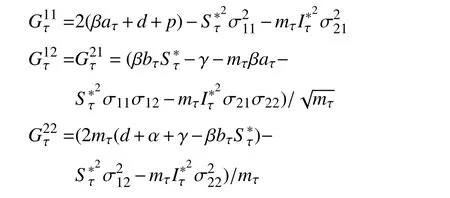
和

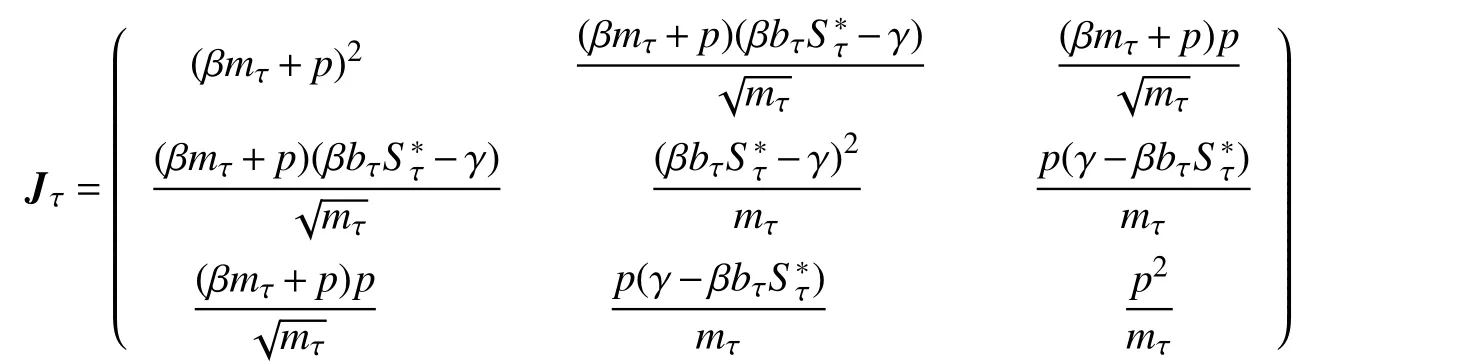
令 |Jτ|=0，可得

定理3如果 τ 和 σij=σi j(τ),i,j=1,2满足下列条件：

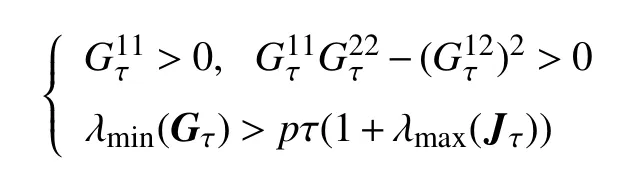
则模型（17）的平凡解是均方指数稳定的。

证明定义：

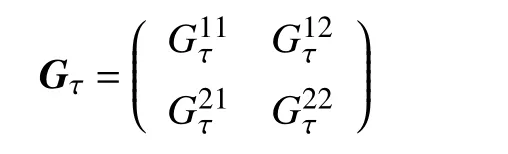
则对所有的 (u1,u2)∈R2，有如下结论：

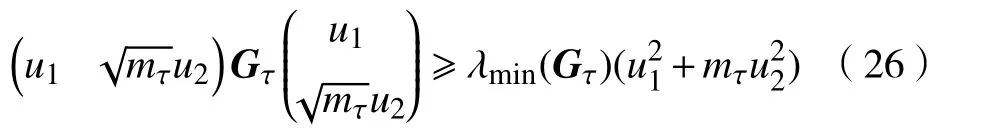
选择 ν2>0，且满足

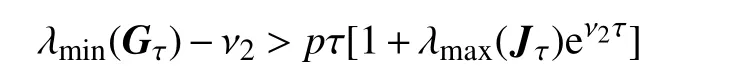
定义一个光滑函数V:R2→R+：

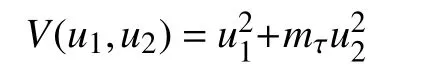
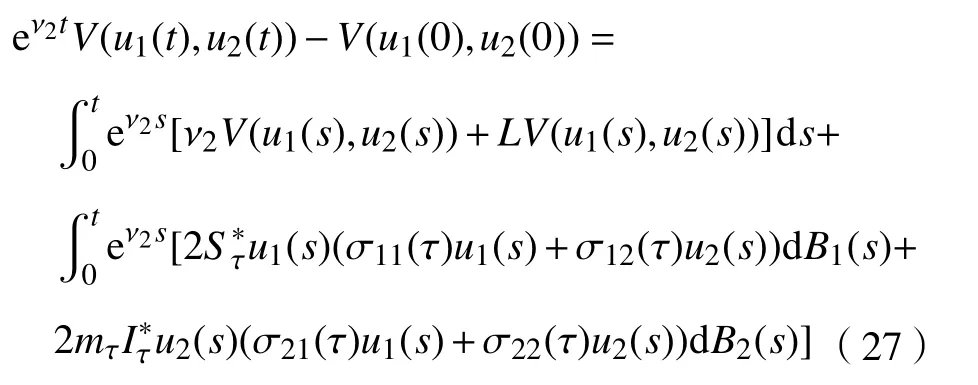
其中，

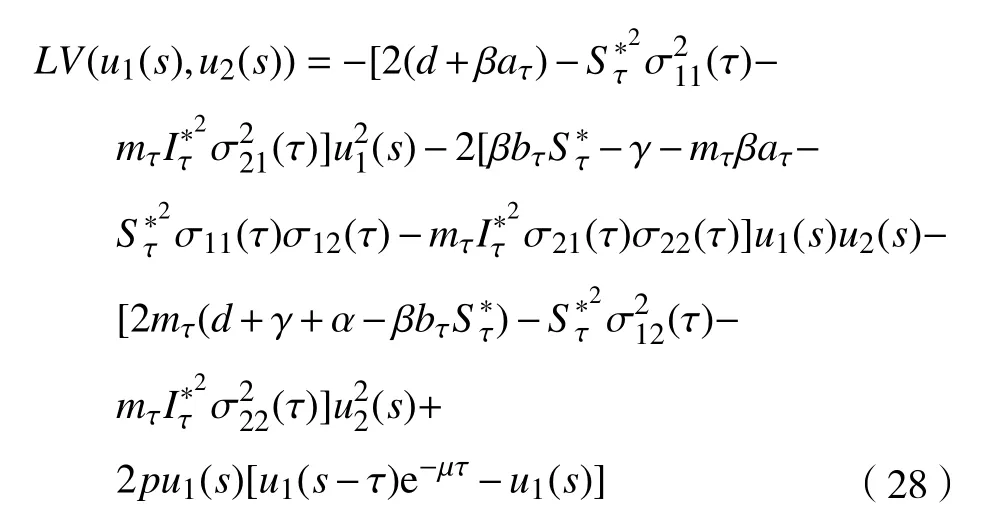
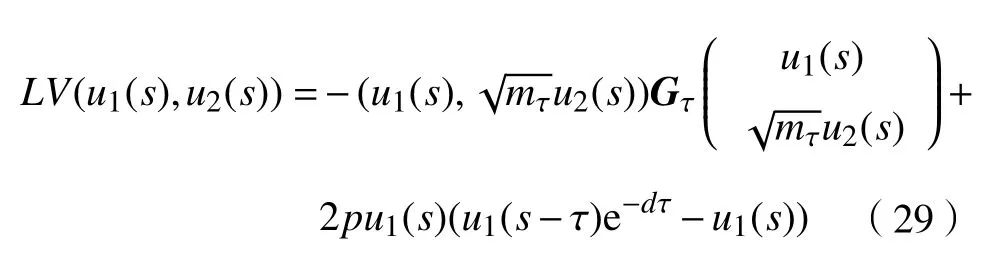
将式（29）代入式（27），并两端取期望，可得

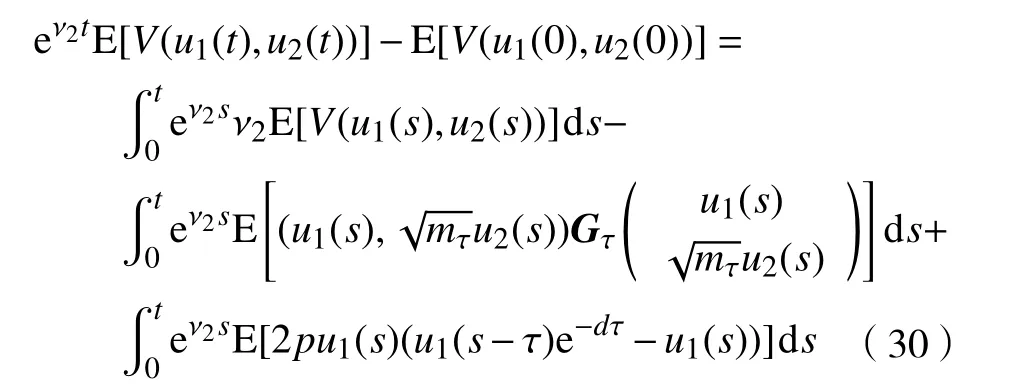
结合式（26）和式（30），显然有下式成立：

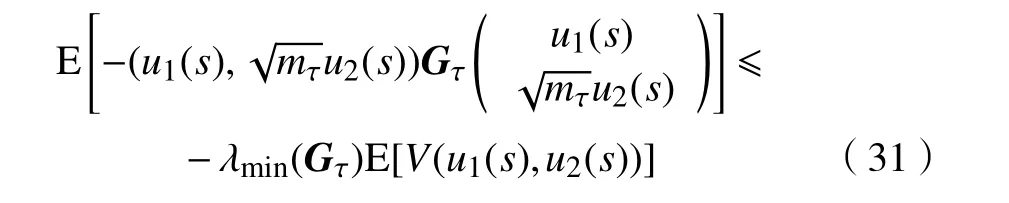
对函数u1(η)edη利用Itô公式，可得

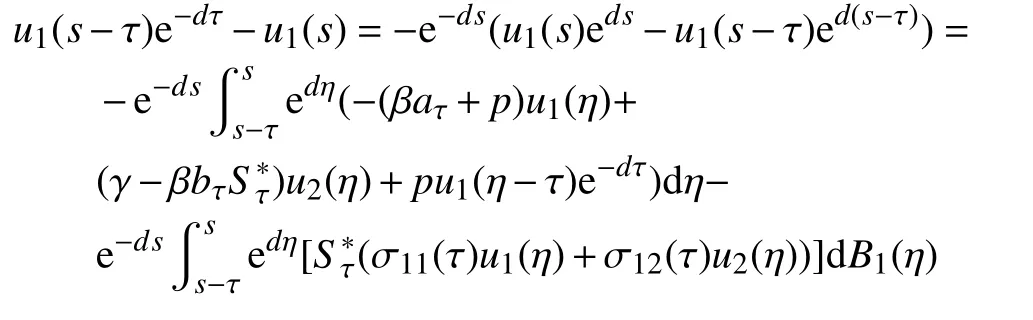
对上式取期望，

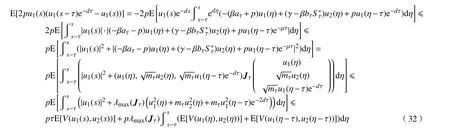
将式（31）和式（32）代入式（30），可得

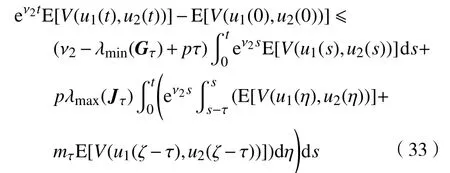
由

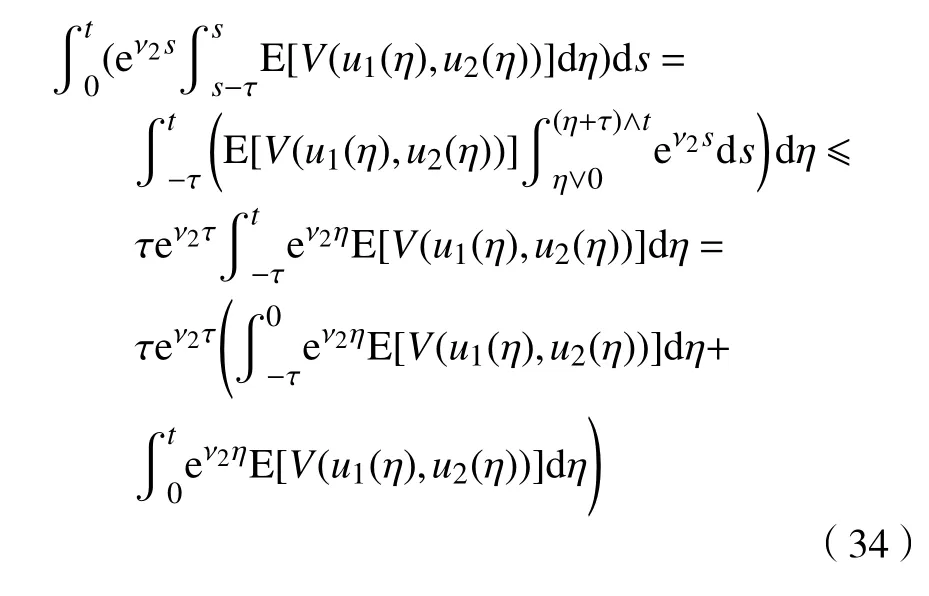
和

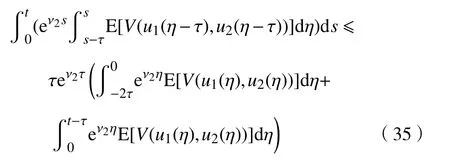
将式（34）和式（36）代入式（33），可得

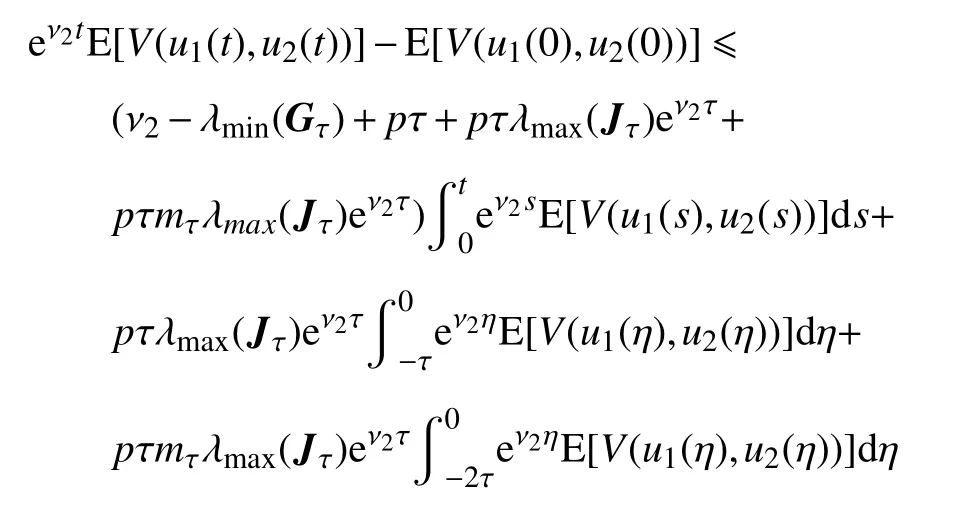
即

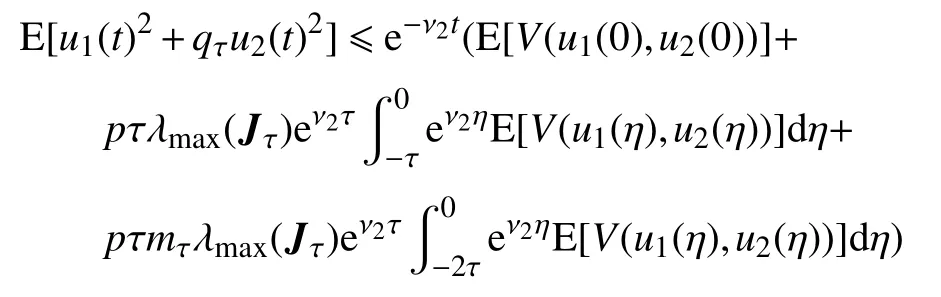
从而证得模型（17）的平凡解是均方指数稳定的，模型（4）正平衡点是均方指数稳定的。

5 模型解的依概率稳定性

现证明模型（4）和式（16）在正平衡点处依概率稳定。

定理4如果 τ 和 σij=σi j(τ),i,j=1,2满足下列条件：

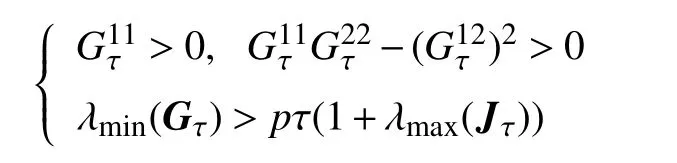
则模型（17）的平凡解依概率稳定。

证明由定理3 的条件可知，存在正常数 ε1和ε2，使得

定义停时：

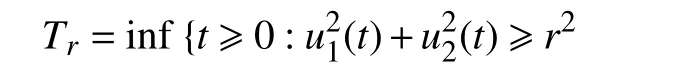
对任意t≥0，由Itô公式可得

其中，LV(u1(s),u2(s))与式（28）或式（29）相同，且

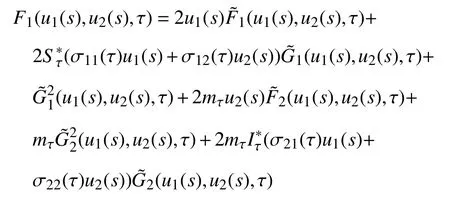
将式（29）代入到式（36）并取期望，可得

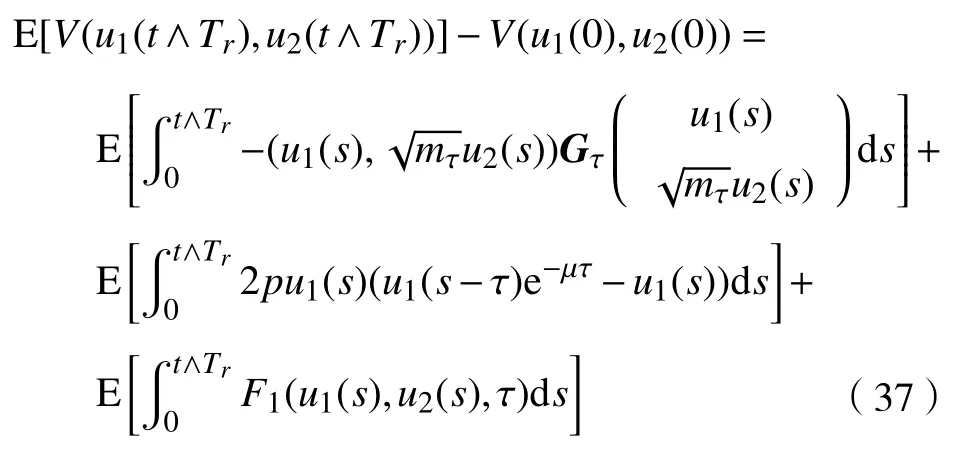
注意到式（37）的第一部分，

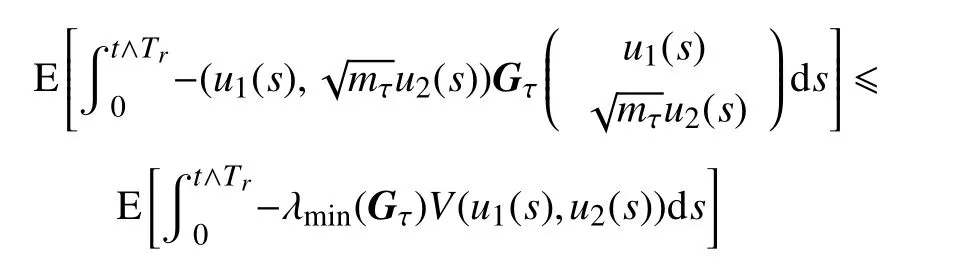
对式（37）第二部分，利用Itô公式可得

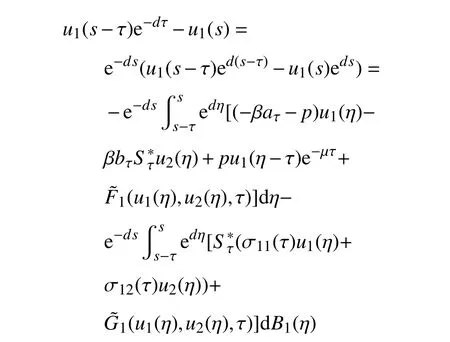
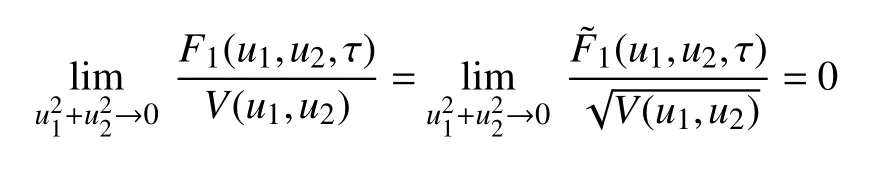
成立。于是， 可以找到一个确定的常数 δ1>0，且满足，使得

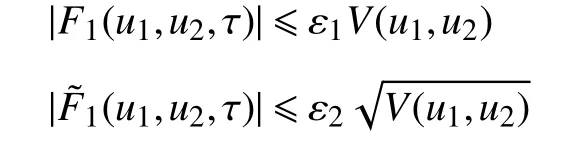
成立。为方便起见，记

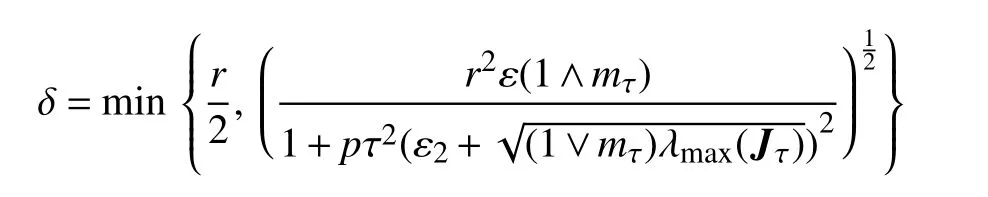
对任意ε ∈(0,1)和r∈(0,δ1)， 且满足‖ξ1‖2+‖ξ2‖2≤δ，可得

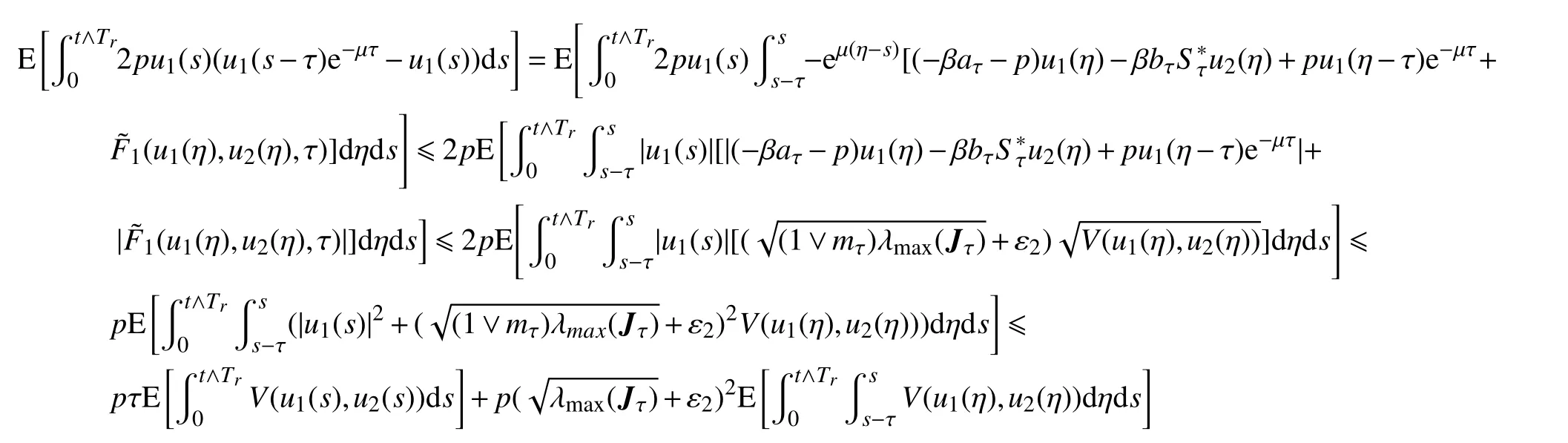
但是，

所以，有

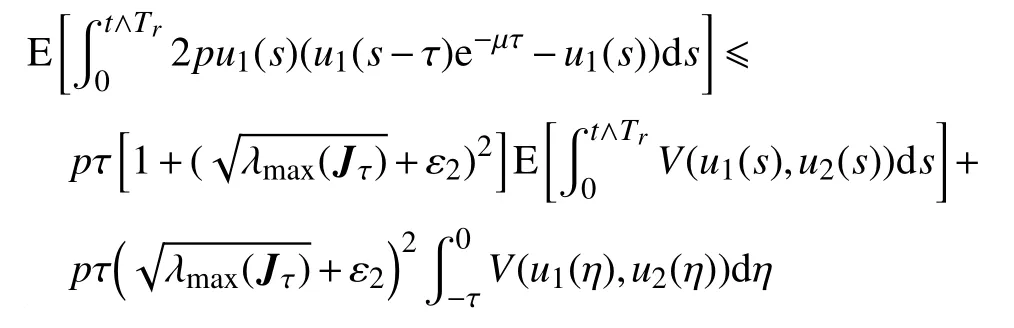
而

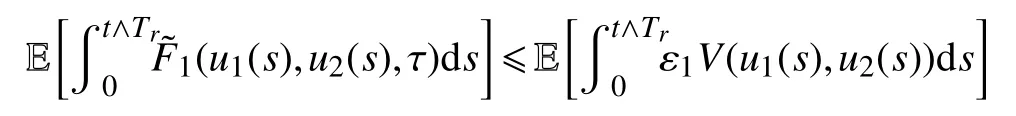
由以上不等式可得

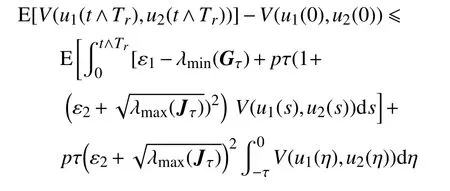
因此，

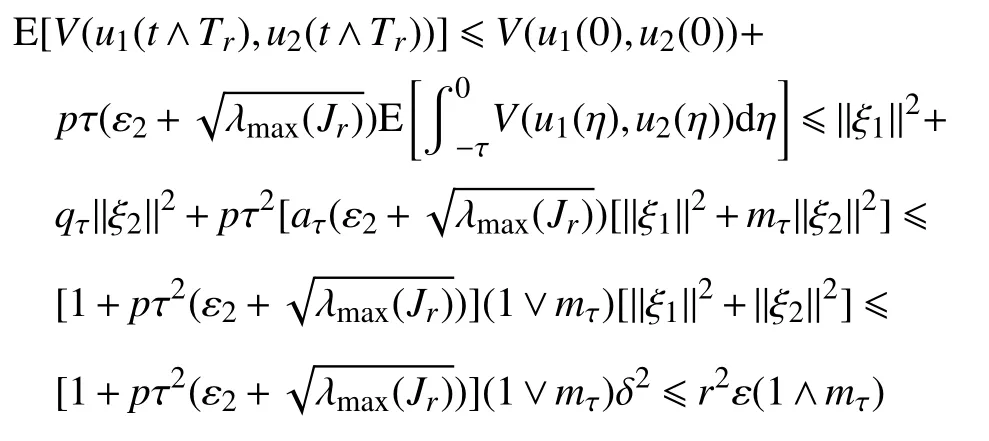
另一方面，

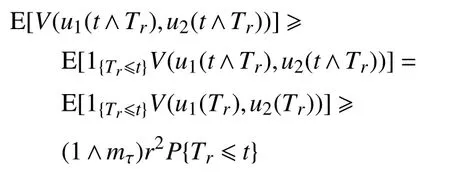
所以，可得P{Tr≤t}≤ε， 令t→∞，则有下式成立：

即平衡点是依概率稳定的。

6 数值模拟

现通过数值模拟分析时滞和白噪声对系统的动力学行为的影响，采用 Euler-Maruyama 作图方法[10-12]对随机模型（3）和对应的确定型模型（2）的解进行计算机模拟，通过图形直观地观测时滞和白噪声对疾病的影响。

在图1 中，通过取不同的 τ值 ，观察 τ对传染病传播的影响，平衡点的值随着 τ值的增大而变小，说明接种后可以控制染病者的传染力，减少疾病的传播。为了更好地对照和比较2 个系统的动力学行为，在图2 中，将确定性模型（2）和随机模型（3）的染病者对应的解曲线体现在同一个图里。由于噪声的存在，使得模型（3）的解围绕着确定性模型（2）的解进行随机震荡。 τ的值越小，模型（3）的解震荡幅度越小。

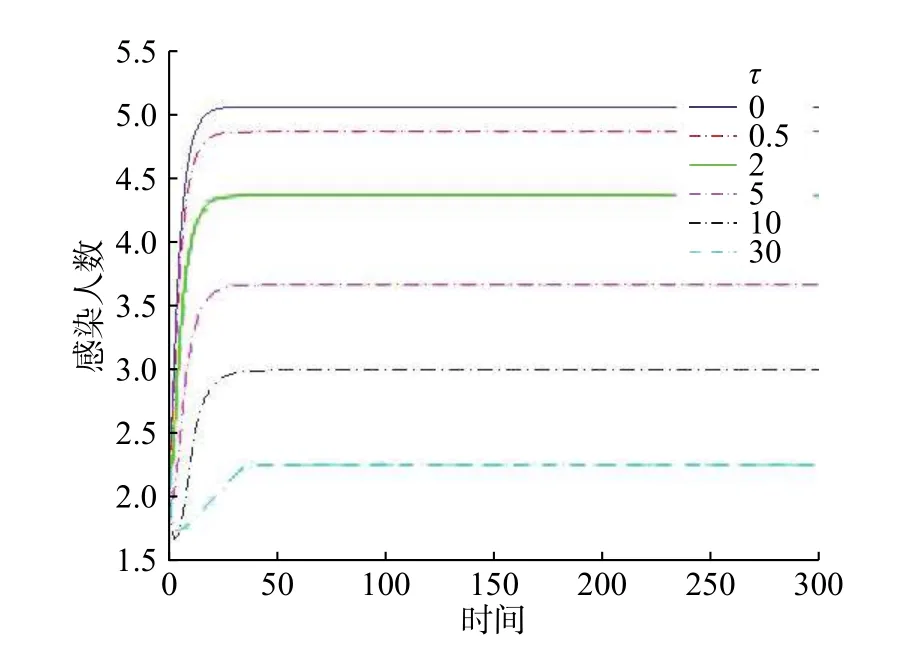
图1 对模型（2）取不同 τ值时，染病者随时间的变化曲线Fig.1 Variation of the infective population with time for different values of delayτ

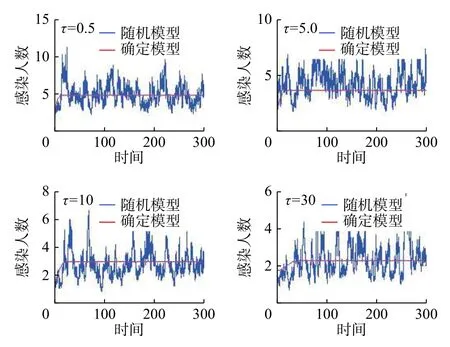
图2 R 0>1，随机模型（3）与确定性模型（2）的染病者的渐近行为Fig.2 Asymptotic behavior of the infective population of the stochastic model (3) and deterministic model (2) when R0>1

本文主要讨论含非线性发生率和时滞的随机延迟SISV 传染病接种模型的动力学行为。首先，证明了模型正解的全局存在唯一性；其次，分别研究了不含时滞和含时滞的随机模型（3）所对应的线性系统的均方指数稳定和依概率稳定。通过分析可知，当白噪声满足一定的条件时带有接种的随机延迟SISV 传染病模型（3）具有均方指数稳定和依概率稳定，即当噪声强度满足一定的条件时，传染病在地方依概率存在使得疾病依然持续流行。