光场成像系统仿真分析与深度标定研究

于成帅, 周 骛, 蔡小舒

（上海理工大学 能源与动力工程学院，上海 200093）

相比于传统成像而言，光场成像能采集整个空间的光辐射分布，经过相位变换和投影积分能得到不同空间位置的图像，能对光辐射直接进行误差校正，达到去除几何像差的目的，能计算出物体的三维结构。光场的概念最早由Gershun 于1936 年提出，用于表征整个空间光线的辐射传输特性[1]。麻省理工学院的Adelson 教授于1991 年将光场表示成7 维的全光函数，并将该概念引入视觉与感知研究，首次提出全光相机模型[2]。Levoy于1996 年将光场简化成光线与2 个平面相交的模型，用4 维参数表示光线的分布[3]。

光场采集方法主要分为两类：多相机组合和单相机改造。斯坦福大学的Wilburn 等设计了几种不同配置的摄像机阵列，每个相机分别位于不同的视角方向，对应光场的一个方向采样，相机中的探测器像元经过镜头投影到外部空间后对应光场的位置采样，通过严格控制各相机的同步时间精度和相对位置精度，能获得高质量的合成图像[4]。但是，由于相机阵列体积较大、费用较高、相机同步控制较复杂等原因，目前只处于实验室研究和商业开发阶段。斯坦福大学的Ng 于2005 年在Adelson 提出的全光相机模型的基础上进行了改进，首次研制出了手持式光场相机，利用数字重聚焦理论实现了先拍照后聚焦[5]。但是，该光场相机的空间分辨率和角度分辨率严重地受到微透镜单元数量的限制。Andrew 于2009 年基于光场相机的方向分辨率冗余性提出了聚焦型光场相机模型[6]，该光场相机的空间分辨率和角度分辨率与微透镜单元的数量无关，只与微透镜阵列与传感器的距离有关，改变这个距离可以调整角度分辨率和空间分辨率。因此，依据微透镜阵列与探测器之间距离的取值范围可以将光场相机分成3 种类型[7]：非聚焦（传统）光场相机、聚焦开普勒型光场相机和聚焦伽利略型光场相机。

在颗粒测量方面，普通相机或者显微镜只能得到颗粒的二维信息，无法得到颗粒的三维信息。光场相机能将普通相机丢失的方向信息记录下来，从而实现单曝光记录整个光场的四维信息，通过处理颗粒表面的光场信号可以测得颗粒的深度或表面三维信息。光场图像的深度信息一般可以通过比较一系列重聚焦图片的清晰度得到[8]。尹晓艮等[9]使用光场数字重聚焦技术结合DFF（depth-from-focus）算法实现物体的三维重建。宋祥磊等[10]提出了光场显微粒子图像测速技术（light field micro-PIV），开展了微尺度流场重建实验研究。刘慧芳等[11]采用基于光场成像理论模型的深度标定方法，实现了光场PTV 方法的颗粒三维速度测量。

本文采用仿真模拟比较了3 种类型光场相机的优缺点，分析了微透镜阵列与传感器距离b对系统景深、焦深以及光圈的影响。综合考虑实际条件和测量对象，搭建了聚焦伽利略型光场相机。其中，b=0.6fm，fm为微透镜单元的焦距。对该相机进行了深度标定实验，并采用仿真系统模拟了实际的深度标定实验，进行对比分析，结果表明，影响深度标定实验准确性的因素为原图清晰度、采样步长、重采样倍数以及拟合方法等。

1 成像原理

1.1 深度标定原理

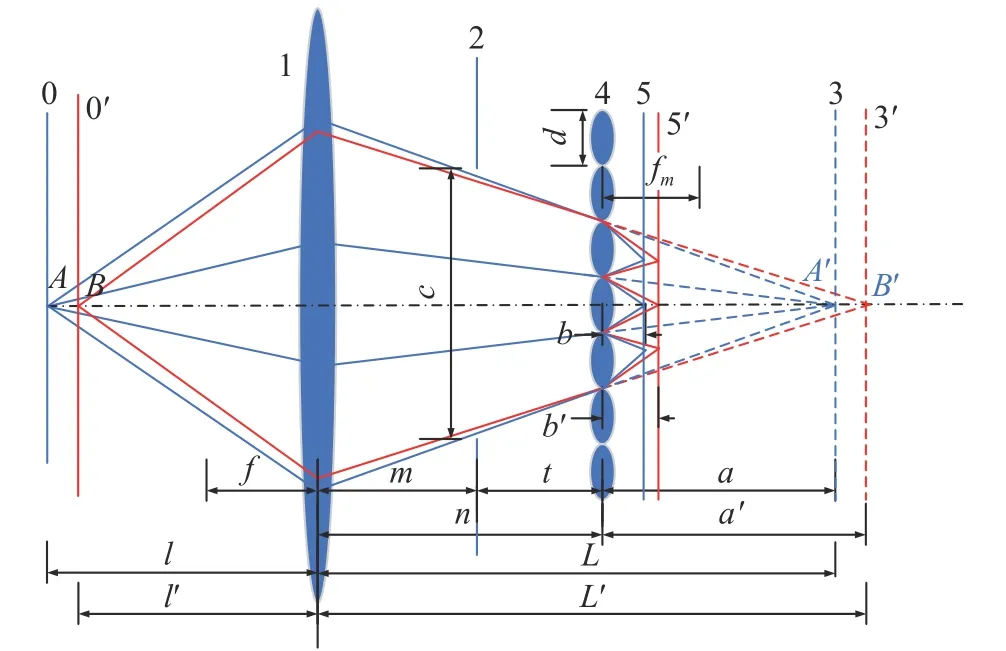
图1 光场相机深度标定原理图Fig.1 Principle diagram of the light field camera depth calibration

伽利略型光场相机成像原理如图1 所示。对于内部参数（f,fm,n,b）一定的系统，轴上理想物点为A，对应的理想像点为A′。轴上其他物点B经过主镜头，对应像点为B′，微透镜阵列对该虚拟像点B′进行二次成像，理想聚焦点将不会落在相机传感器上，反而会在传感器上形成弥散圆，使图像变得模糊。图1 中l为理想物距，L为主镜头理想像距，l′为重聚焦物距，L′为主镜头重聚焦像距，a为微透镜阵列物距，b为微透镜阵列与传感器距离，a′为重聚焦后微透镜阵列的物距，b′为重聚焦后微透镜阵列与传感器距离，n为主镜头主平面到微透镜阵列的距离，m为主镜头与光阑的距离，t为光阑与微透镜阵列的距离，f为主镜头焦距，fm为微透镜单元的焦距，d为微透镜单元孔径，c为光阑孔径。根据重聚焦理论，光线到达传感器沿着原来的方向继续传播将会聚焦在传感器后面某个位置，因此，该位置对应的重聚焦图片将会是最清晰的。对于某一重聚焦系数α，有如下关系式：

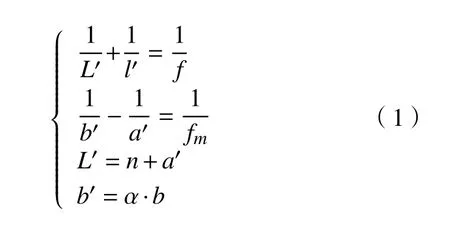
经过代数整理后可得

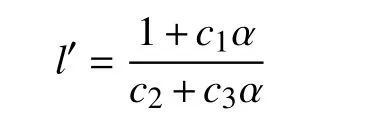
其中，

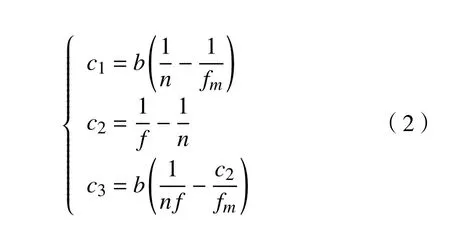
式中，c1，c2和c3均为系统常数。

在系统内部参数b，n，f，fm不变的情况下，不同的重聚焦系数α对应不同的像面5′，对应不同的主镜头成像虚拟面3′，对应不同的物面0′。因此，只需要找到每个位置对应的最优重聚焦系数[11]，就能求出c1，c2和c3，进而根据式（2）求出重聚焦系数所对应的实际深度l′。式（2）同样适用于聚焦型开普勒光场相机和传统光场相机。

1.2 系统景深与焦深计算

根据式（2）还可以计算重聚焦系数与景深、焦深的关系。只要物点经过系统所形成的像点的弥散斑小于像素的宽度，就认为像仍然是清晰的，对应的物方成像范围称作景深[4]。像面的允许变化范围即焦深，其计算式为[7]

式中：Δx为系统焦深；p为像素尺寸。

对于不同的系统，即b的值不同，其将拥有不同的焦深，且焦深与b成正比。而对于同一个系统，即b为固定内参时，其将对应一定的焦深。将焦深转换为该系统允许清晰成像的重聚焦系数，就能得到对应的景深。所以，景深Δl的计算式为

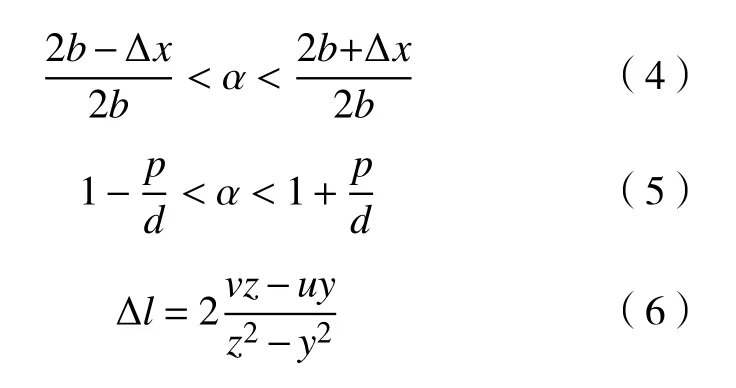
其中，

在参数p，d，f，fm不变的情况下，不同的b决定了主镜头主平面到微透镜阵列的距离n，b与景深Δl之间存在一一对应的关系。当镜头与光场传感器（微透镜阵列与传感器的组合）确定的情况下，可以根据式（3）和式（6）计算不同b对应的系统焦深和景深。

2 3 种类型光场相机比较研究

为了搭建一套可用于微颗粒表面形貌测量的光场相机成像系统，使用光学仿真软件Zemax 对光场相机的3 种类型分别进行模拟，比较它们的优缺点，最终选择其中1 种类型进行实验研究。

2.1 仿真系统的搭建

仿真系统主要包括主镜头、光阑、微透镜阵列和探测器。主镜头的主要参数为波长、视场、焦距以及F#（焦距/入瞳直径）。光阑的主要参数为孔径。微透镜阵列的主要参数为微透镜单元的数量、孔径和F#。探测器的主要参数为像素数和像素尺寸。仿真系统的参数与实验系统相关参数保持一致，系统各元件主要参数如表1 所示。

光阑与微透镜阵列之间的距离满足关系式：

表1 系统元件参数Tab.1 Table of the system element parameters

光阑孔径代表着系统的出瞳直径，由如下公式计算：

为了比较3 种光场相机的成像特点，在设计不同光场相机成像系统时，假设主镜头与光场传感器参数固定，即在p，d，f，fm不变的前提下，保持主镜头与光阑的距离m不变，物距不变，像距L也不变，将光场相机的微透镜阵列与探测器之间的距离b作为变量，其他系统参数按照式（8）和式（9）进行计算，共仿真了9 套成像系统，系统参数如表2 所示。

根据式（3），（6）和（9）分别计算不同b对应的系统景深、焦深和光圈直径，并绘制出曲线，如图2 所示。

由图2 可知，聚焦型光场相机的焦深随着b的增加而增加，光圈随着b的增加而减小，但是，伽利略型光场相机的景深随着b的增加而增加，开普勒型光场相机的景深随着b的增加而减小。传统光场相机的景深相对较大。9 套系统计算得到的结果如表2 所示。

表2 仿真系统参数表Tab.2 Table of the simulation system parameters

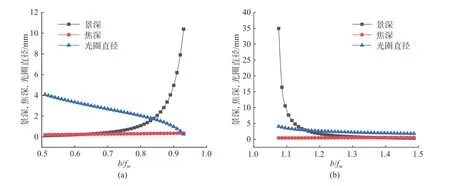
图2 系统景深、焦深、光圈大小与b 的关系曲线图Fig.2 Relationship between b and the system depth of field, focal depth and aperture size

在Zemax 零件设计器中通过脚本文件自定义四边形非完全填充型微透镜阵列，采用混合模式建立以上9 套成像系统，图3 为仿真软件建立的四边形非完全填充型微透镜阵列外观图和系统轮廓图。

图3 仿真系统轮廓图Fig.3 Outline of the simulation system

2.2 仿真结果

仿真与实验标定图如图4 所示。对每个成像系统，利用Zemax 几何位图分析功能[12]将图4（b）以相同大小放置在与镜头相同距离的位置，得到一张包含分辨率信息的原始光场图，如图5 所示。再用一张白色图片得到一张包含微透镜中心坐标信息的白板图，用于仿真标定实验。

图4 仿真与实验标定板图Fig.4 Simulation and experimental calibration charts

2.3 分 析

对于传统光场相机而言，空间分辨率等于微透镜单元的数量，角度分辨率等于每个微透镜单元下覆盖的像元数，即空间分辨率和角度分辨率完全取决于微透镜单元的数量和尺寸。但是，当微透镜单元的尺寸很小时，每个微透镜单元所形成的子图像就会因为边缘效应产生噪声和不可信的结果。为了克服边缘效应，每个微透镜单元下的像素数相对要多一点，这样就无法得到较高的空间分辨率，限制了传统光场相机的功能[13]。而且由于微透镜单元的衍射效应，要求子孔径经过微透镜单元产生的艾里斑直径不超过像素的宽度[4]，也间接限制了传统光场相机的用途。

对于聚焦型光场相机，原始光场图片经过渲染得到的空间分辨率等于传感器分辨率乘以b/a，角度分辨率等于a/b，将图4 中（a）～（d）以及（f）～（i）放大能看到小男孩的鼻子被越来越多的微透镜单元成像。由于b的取值范围要满足式

渲染图像的分辨率将随着a的减小而增加。聚焦型光场相机的空间分辨率和角度分辨率之间的平衡关系与微透镜数量无关，因此，可以采用相对大尺寸的微透镜单元克服边缘效应。

景深将对光场相机的深度分辨能力产生影响。景深越大，系统越难以分辨微小的物体；景深越小，将越能提高系统的深度分辨率。经过综合考虑，根据测量要求和实际条件，选择b=0.6fm的聚焦型伽利略光场相机。

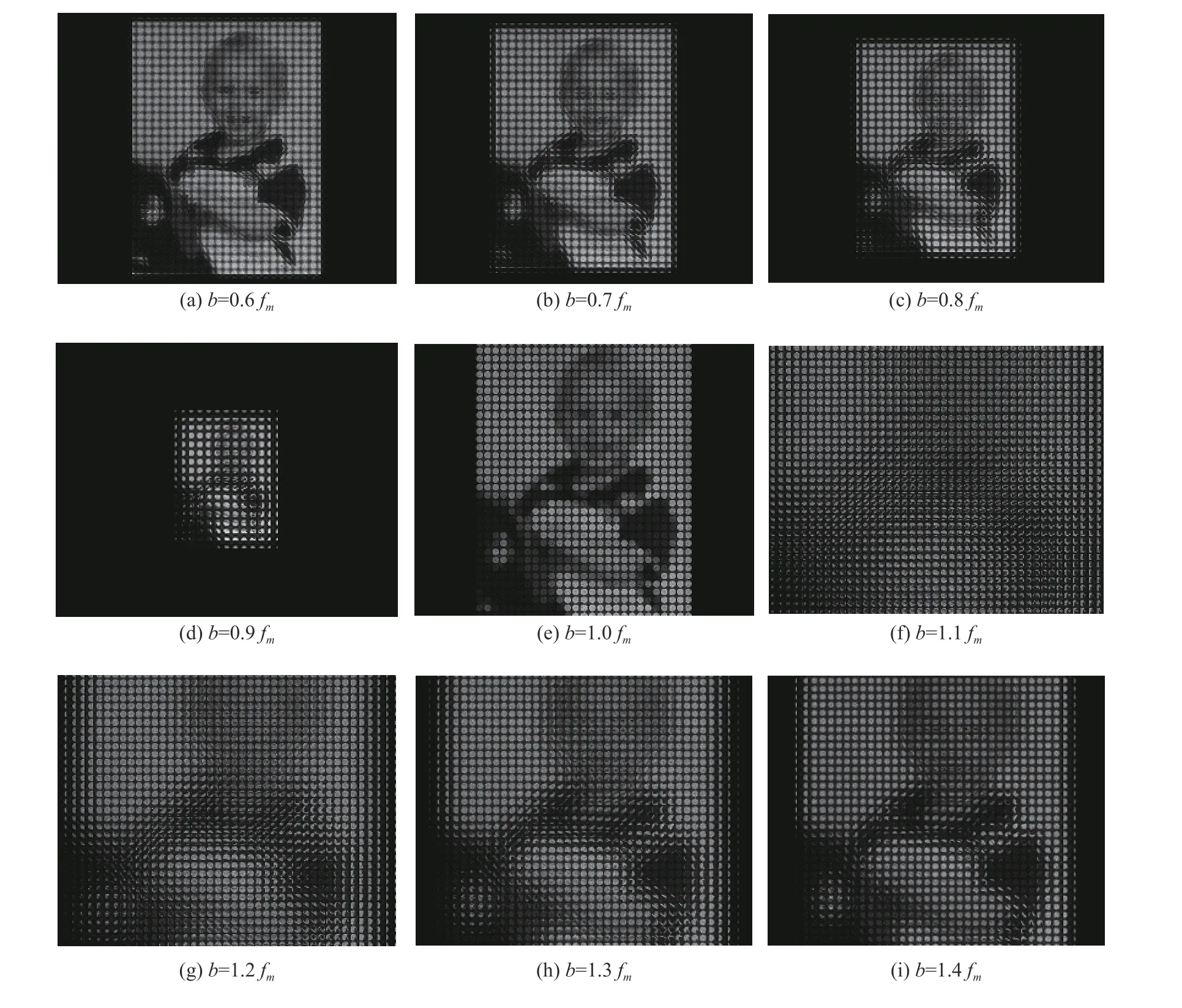
图5 不同系统仿真结果图Fig.5 Simulation results by different systems

3 实验系统搭建与深度标定分析

3.1 光场相机的搭建

根据表3 搭建了变倍的聚焦伽利略型光场相机，如图6 所示。主镜头型号为索雷博的TRS254-040-A 的三胶合透镜，焦距为40.6 mm；型号为SM1NR1 的可伸缩镜筒，实测行程52.8 mm；型号为SM1D12C 的可调光圈，可调范围为1～12 mm；型号为MLA150-7AR-M 的四边形非完全填充型微透镜阵列，边长为150 μm，焦距为5.5 mm，材料为Silica；相机采用的是IDS 生产的型号为UI-1242LE-C 的板式相机，像元尺寸为5.3 μm，分辨率为1 280×1 024。

表3 搭建的光场相机参数表Tab.3 Table of detail parameters of the self-built light field camera

相机的光阑处于主镜头与微透镜阵列之间，即系统的出瞳就是该光阑，并且保持光阑、微透镜阵列以及探测器之间的距离不变。随着主镜头与光阑之间距离的变化，也就是像距发生变化，对应的物距随之发生变化，但是，主镜头的一次成像面相对微透镜阵列的位置不变。

3.2 深度标定实验

3.2.1 仿真分析

图6 光场相机外观与内部结构图Fig.6 Appearance and internal structure of the self-built light field camera

在Zemax 混合模式下，建立与实际系统参数一致的仿真系统。采用图4 中（a），（b），（c）3 种不同参数的标定板按照不同的实验方案进行深度标定实验，标定板参数如表4 所示，实验方案参数如表5 所示。其中，系统的空间分辨率为3.3 lp/mm，标定板的空间分辨率要小于系统的空间分辨率。对每组原始光场图片进行重聚焦处理[14]，得到每组重聚焦图片的清晰度与重聚焦系数的关系曲线，仿真曲线如图7 所示。最终得到最优重聚焦系数与深度位置的关系曲线，仿真数据如图8所示。对图7 中的仿真曲线进行8 次多项式拟合，得到图7 中的拟合曲线，以此得到深度标定结果，如图8 中的清晰度拟合得仿真数据所示。对图8 中的清晰度拟合得仿真数据进行3 阶多项式拟合，得到图8 中的三阶多项式拟合曲线；对图8 中的清晰度拟合得仿真数据根据式（2）拟合，得到图8 中的理论公式拟合曲线。图8 中（a），（c），（e）的重聚焦图片在生成过程中在空间分辨率上进行了4 倍的重采样，图8 中（b），（d），（f）的重聚焦图片在生成过程中没有进行空间分辨率上的重采样。

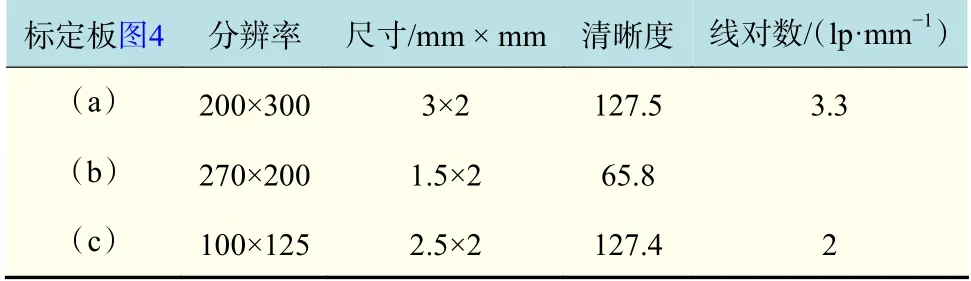
表4 仿真标定板参数与实验参数Tab.4 Simulation calibration board parameters and experimental parameters

对图8 的（a），（c），（e）进行比较，（a）和（e）的结果更加符合理论公式，说明图片的清晰度是主要影响因素之一。对比每张标定图片得到的仿真数据结果，发现（a），（c），（e）分别优于（b），（d），（f），说明在生成重聚焦图片的过程中空间分辨率重采样倍数也是主要影响因素之一。其中，（b），（d），（f）的仿真数据出现很大的跳跃，这是由于在生成重聚焦图片的过程中没有进行插值运算，导致生成的重聚焦图片的分辨率等于宏像素单元数，而且系统存在一定的景深，在此范围内移动标定板得到的原始光场图将没有明显的变化，导致每组最清晰的重聚焦图片对应的最优重聚焦系数都是一样的。对比图8 中的仿真数据与清晰度拟合得仿真数据，发现对每组清晰度重聚焦系数曲线的拟合也是影响标定结果准确性的因素之一。此外，重聚焦系数步长越小，图8 中的曲线越光滑，标定结果也会越准确。位置采样步长不能太小，否则会造成相邻两张原始光场图片重聚焦图片清晰度变化不明显，就会造成2 个位置具有相同的最优重聚焦系数，从而影响最终的深度标定曲线。

表5 仿真实验参数Tab.5 Simulation experiment parameters

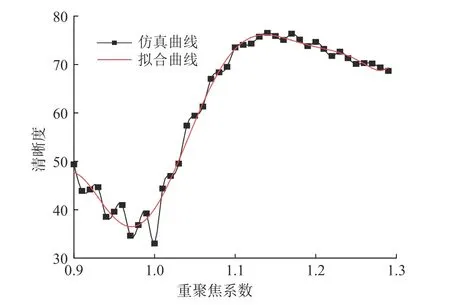
图7 某一深度位置重聚焦系数与清晰度的关系曲线图Fig.7 Relationship between the refocusing coefficient and the clarity

图8 仿真系统深度标定结果图Fig.8 Depth calibration diagram of the simulation system

3.2.2 实验研究

对实验系统也采用3 种不同参数的标定板进行深度标定，图4 中（a），（c），（d）标定板参数如表6 所示，3 种实验方案的参数如表7 所示。3 组实验结果如图9 所示。其中，图9（a）和（c）与理论公式拟合结果很吻合。对于图9（b）中出现的阶跃曲线，是由于采样步长过小，实验中使用的位移平台精度不够高，以及实验中经过标定板的光线被漫反射板过滤而导致棋盘格的清晰度较低等综合因素造成的。

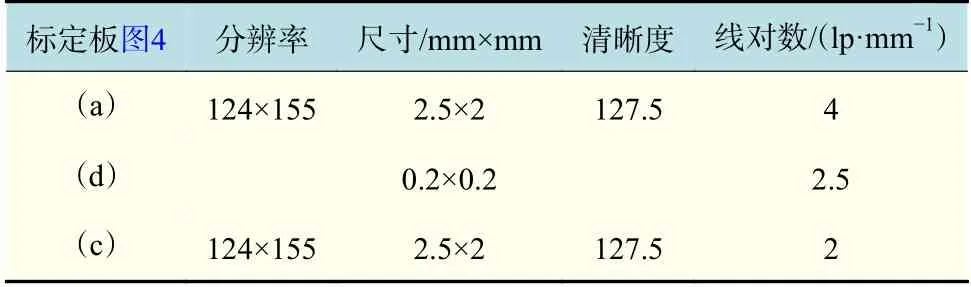
表6 实验标定板参数表Tab.6 Experimental calibration board parameters

表7 物理实验参数表Tab.7 Physical experiment parameters

综上所述，该深度标定方法的影响因素主要包括原图的清晰度、重聚焦图片空间分辨率重采样倍数、清晰度重聚焦系数曲线拟合、采样步长及重聚焦步长等。在使用该方法时，标定板的空间分辨率应小于光场相机的最大空间分辨率，并且边缘梯度要较大。在移动标定板采样的过程中间隔不小于景深。在生成重聚焦图片的过程中使用较小的重聚焦系数步长以及进行空间分辨率上的重采样。在处理每组重聚焦图片清晰度与重聚焦系数的关系中采用高阶多项式拟合。

4 结束语

搭建一套可用于微颗粒表面形貌测量的光场相机成像系统，使用光学软件Zemax 对3 种光场相机分别进行仿真，改变微透镜阵列与探测器之间的距离，得到了9 张仿真图。通过微透镜中心坐标的标定得出传统型光场相机的空间分辨率和角度分辨率。对于聚焦型光场相机，空间分辨率与角度分辨率仅与微透镜单元的a和b有关，与微透镜单元的数量无关。因此，可以使用相对大尺寸的微透镜单元克服边缘效应，增加相机传感器的像元利用率。得出微透镜单元与传感器之间的距离b与系统景深、焦深和光圈直径的关系曲线。综合考虑实际条件和测量对象，选择搭建b=0.6fm的聚焦新伽利略光场相机。

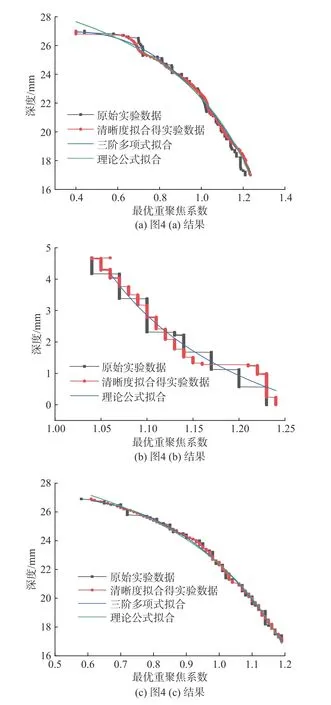
图9 实际系统深度标定曲线图Fig.9 Depth calibration curve of the actual system

对搭建的这套光场相机进行深度标定，得到实验条件下的深度标定曲线。采用仿真手段研究影响深度标定方法准确性的因素，结果表明，原图清晰度、采样步长、重聚焦步长、重采样倍数以及拟合方法都对最终得到的深度标定曲线产生影响，并通过改进实验验证了仿真的结论。为下一步进行颗粒三维表面的深度重构奠定了基础。

[][]