低复杂度极化码优化译码算法研究
李潇云,侯 磊,张正平
(贵州大学大数据与信息工程学院,贵州贵阳 550025)
0 引言
一个简单的通信系统模型包含信源、信道、信宿3 个部分,该通信系统模型被称为香农范式。在现实生活中,通信系统里的信道一般都是有噪信道,在有噪信道中使用信道编码,可以极大提高通信系统的可靠性[1]。多年来,人们设计出了许多性能优异且高效的信道编码,比如LDPC(低密度奇偶校验)码[2]和Turbo 码等,这两种都是性能逼近香农极限的信道编码[3]。2008 年,Erdal Arikan 教授在国际信息论会议中,首次提出了信道极化这一概念,并在2009 年提出基于信道极化理论的极化码,极化码是目前确定的能被证明达到香农极限的信道编码,在SC(串行抵消)译码算法下,当码长N 趋近于无穷大时会达到信道的信道容量[4]。但是在中短码长下SC 译码算法的性能并不理想,极化码自被提出以来,就引起了科研人员的广泛关注,为了提高其性能,基于SC 译码算法的SCL(连续列表)译码算法[5]、增加了循环冗余校验(CRC)辅助的SCL 译码算法[6]以及BP(置信度传播)译码算法[7-8]相继被提出。本文详细描述SC译码算法的解码结构,介绍加入了列表的SCL 译码算法与加入了循环冗余校验的CA-SCL 译码算法,并提出一种低复杂度极化码优化译码算法PB-SCL,随后将使用这几种译码算法的极化码进行性能比较并分析,使极化码能在未来通信和实际生活中得到更加广泛的应用。
1 信道极化现象与编码原理
1.1 信道极化原理
极化码构造的核心是信道极化,而信道极化原理可以简单概括为信道合并与信道分裂。Arikan[9]在设计极化码时,主要在二进制离散无记忆信道(B-DMC)中进行,极化思想即是N 的独立不相关的B-DMC 信道经过信道合并和信道分裂后形成N 个相关信道。
信道合并[10]:已知一个B-DMC 信道W:X→Y,转移概率为W(y|x),其中x∈X,y∈Y。在B-DMC 信道W经过N次递归后,产生的信道WN:XN→YN:

其中,N为2 的幂次,N=2n,n≥0。

信道分裂:WN表示对信道合并后W的N次使用,然后将组合信道WN分裂成N 个独立不相关信道的过程,W(i)N:X→YN×Xi-1,1 ≤i≤N,其转移概率即:
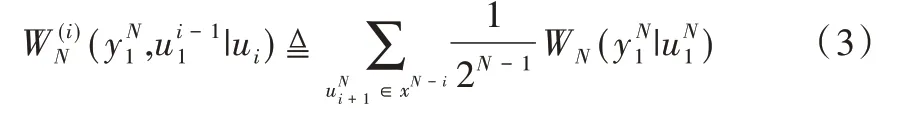
根据极化码的信道极化原理[11],可知对任意N=2n,n≥0,1 ≤i≤N 2 的极化信道,都有奇序列分裂子信道与偶序列分裂子信道两个递归式转移概率:

1.2 信道极化现象
信道极化现象指当极化码的码长N=2n,以2 的幂次趋近于无穷大时,极化码输入比特序列信道的信道容量就会呈现出两极分化现象,明显地趋于两个极端:一部分信道容量为0 的纯噪声信道,以及其余信道容量为1 的无噪声信道[12]。二进制对称信道(BSC)与二进制删除信道(BEC)都是满足对称性的二进制离散无记忆信道(BDMC),假设在满足BSC 信道中信道容量I(w)=1+p*logp+(1-p)*log1-p,在BEC 信道中I(w)=1-p,转移概率p=1/2,随着极化码的码长以2 的幂次逐渐增大,呈现出的两个极端将会越来越明显。
图1、图2 分别为在BSC 信道或BEC 信道下码长N=64和N=128 的信道极化仿真图,此时信道极化现象并不是那么明显。

Fig.1 N=64 channel polarization diagram图1 N=64 信道极化图
当码长N≥512 时,大部分信道都得到了充分极化,图3-图4 分别为码长N=512 和N=1 024 的信道极化仿真图,此时信道极化现象已经得到充分证实,当码长趋近于无穷时信道容量会呈现两级分化[13]。因此,可以利用该信道极化现象,将部分信道容量趋近于0 的纯噪声信道用来存储冻结比特,而将其余信道容量趋近于1 的无噪声信道用来存储信息比特。

Fig.3 N=512 channel polarization diagram图3 N=512 信道极化图
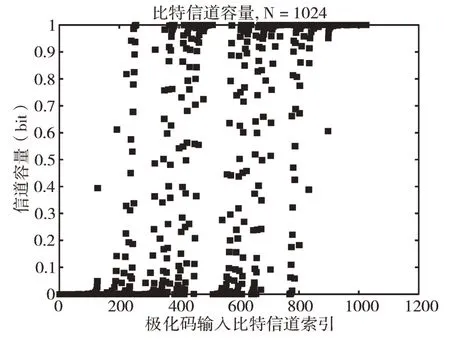
Fig.4 N=1 024 channel polarization diagram图4 N=1 024 信道极化图
1.3 极化码编码原理
极化码编码原理是利用极化现象进行构造的编码,选择合适承载信息比特的信道和放置冻结比特的信道,随后进行数字逻辑运算的过程。给定原始比特序列=(u1,u2,…,uN),编码后的比特序列=(x1,x2,x3,…,xN),因此可以显式地将编码原理表示出来:

其中,GN为N阶生成矩阵,N=2n[14],体现了对信息比特序列承载信道的选择与固定比特序列承载信道的选择,进而可以将上式表示为:

其中,∧代表承载信息比特序列的集合,∧c代表承载固定比特序列的集合,GN(∧)代表N 阶生成矩阵中取与∧中元素对应信道组成的生成矩阵,GN(∧c)则表示取与∧c(固定序列比特集合)中对应元素构成的生成矩阵。只需要确定存放信息比特和固定比特的信道,就可轻松得到编码后的比特序列[15]。
2 极化码译码算法
2.1 SC 译码算法
SC 译码算法的数学模型,即进行递归译码的过程,从以上极化码编码原理可知,存在一个选择存放信息比特信道和存放固定比特信道的过程,由此可以定义出一种线性陪集码(N,K,∧,u∧c)[16]。其中,K 表示信息比特数量,∧为信息位指定存放位置、元素数量为信息比特数量K,u∧c为固定位、元素数量为冻结比特数量N-K。通常固定比特统一取值为0,因此固定比特u∧c取值不会出现错误,将其恒定为0,因此SC 译码算法的译码原理就是对信息位∧的估值。

进而可以直接通过计算对数似然比LLR 值对比特进行估值判决:
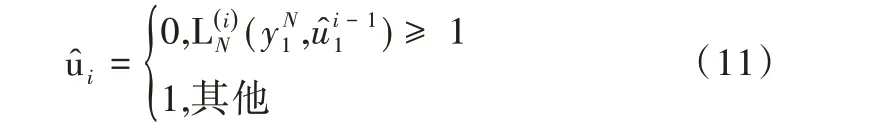
根据式(4)与式(5)这两个奇序和偶序分裂子信道,SC译码器的复杂度为O(NlogN),则每个LLR 值也可通过奇偶性进行计算,则可得到对数似然比LLR 值的奇偶性公式[16]。
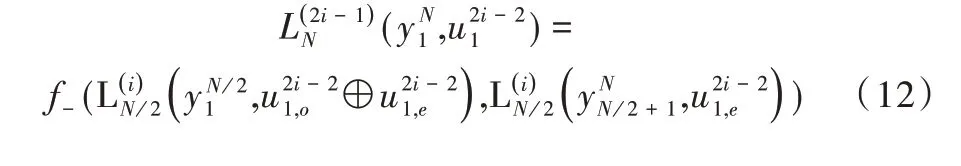
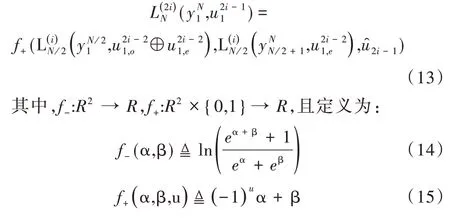
其中,α,β ∈R,u ∈(0,1)。
当N=8 时,SC 译码栅格图如图5 所示。
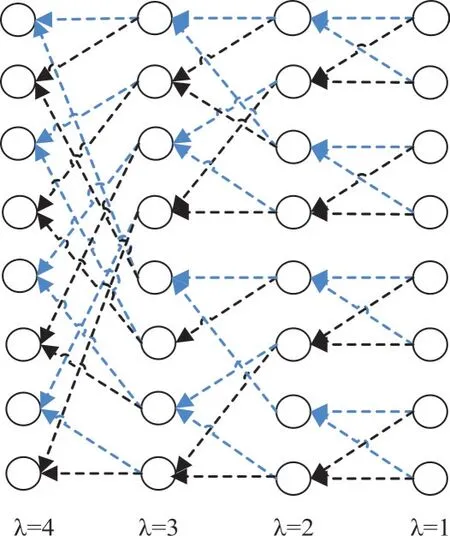
Fig.5 SC decoding grid map图5 SC 译码栅格图
图中灰色箭头和黑色箭头分别表示f-与f+从右端开始递归的过程,且右端开始λ 表示处于的层级,从右向左λ=(1,2,3,…,n),总共有logN层。图中每一个节点代表一个LLR 值,则LLR 值从上到下表示为,i=(1,2,3,…,N),从而可以通过上述递归式对进行计算,最后对比特进行估值判决,若≥1,则判决为=0,其他则判决为=1。SC 译码算法以LLR 为判决准则,对每一个比特进行硬判决,按比特序号从小到大的顺序依次判决译码[17]。
2.2 SCL 译码算法
SC 译码算法是对比特进行硬判决的过程,只选择一条其认为最优的路径进行探索。但是在极化码码长有限的情况下,信道极化现象不明显,如果直接对子信道的比特序列进行硬判决,会由于信息量不够而导致错误译码。针对这一现象,引进了SCL 算法,SCL 算法是在SC 算法的基础上,通过保存L 条具有PM(路径度量)值的路径进行下一层解码,在算法的最后选取一条具有最小PM 值的路径,即相对于SC 算法,SCL 算法增加了路径保存和回退功能[18]。
即对于SCL 译码算法,存在L 条路径同时进行遍历,同时也要对L 条路径进行PM 值评估,选择最优路径进行译码,PM 值的定义为:

其中,l∈{1,2,…,L} 为路径索引,第l条路径,i∈{1,2,…,N}为第i个比特位,对数似然比LLR,=
图6 为极化码的一种二叉树表示方法。
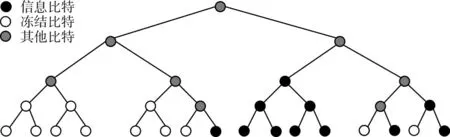
Fig.6 Polarization code decoding binary tree图6 极化码译码二叉树
搜索宽度L=2,从上到下进行遍历,包含PM 初始化、路径扩展、路径选择、路径删除和判决输出的过程。图中每一个节点的译码路径都对应一个PM 值,首先对PM 值进行初始化,使L(1)=∅,PM(1)=0。使其向下搜索并扩展,当译码到第i个比特时,对列表Li-1里的每一条路径进行扩展,分别根据左右路径进行扩展,将扩展后的路径记录在列表Li中。如果Li中路径数目大于列表L,根据LLR 值计算出PM 值删除或保留相应路径,保留PM 值最小的L 条路径,其余路径删除[18]。

最后根据PM 值选出最优路径,对比特序列判决后译码输出。
循环冗余校验(CRC)辅助编码是通信系统中的常用技术。其目的是对传输信道上传输的数据进行校验和检测,加入了CRC 的串行消去列表解码(SCL),可以删除掉与CRC 不符合的路径[19]。首先将CRC 与极化码共同进行编码,随后与SCL 译码方式相同,将SCL 译码序列交给CRC 进行校验、筛选。对于确定的信息位P,其中包含了CRC 校验位p 和信息比特位K,则P=K+p。
SCL 译码算法结束时列表中存有一组候选的译码结果,因而便于将极化码与CRC 进行联合检测译码,即将通过CRC 校验且PM 值最小的序列作为译码输出结果。CASCL 译码算法相较于SCL 译码算法,加入CRC 辅助路径校验选择,提高了极化码译码算法的性能。
3 低复杂度极化码优化译码算法PB-SCL
与SC 译码算法相比,SCL 译码算法可以大幅度提升极化码译码性能,但是同时增加了复杂度和时延[20]。SC 译码算法的时间复杂度为O(NlogN),而SCL 译码算法的时间复杂度为O(LNlogN),会随着L 列表宽度的增大而增大。因此,为了降低SCL 译码算法复杂度,引入优化的剪枝PBSCL 译码算法。
如图6 所示,用Dv表示节点v的深度,Vv表示以节点v为根节点的子树中所有节点的集合,其中变量节点记为Iv,图中黑色节点表示信息比特,白色节点表示冻结比特,灰色节点表示C 除去信息比特与冻结比特的其他类型的子码。表示在第l条译码路径中输入以v为根节点的子码的软信息向量。SCL 译码算法在对第i个比特进行译码时,必须要对i-1 个前的整个译码树进行搜索,因此可以从二叉树的角度理解,缩小需要串行遍历的二叉树结构。对于以节点v为根节点的子码,如果叶子节点都是冻结比特,在译码时就要直接略过这些冻结比特的节点。

利用优化的剪枝SCL 译码算法进行译码,可以对极化码中所有的冻结比特略过不计,这时就可以缩小需要串行遍历的二叉树,如图7 所示。
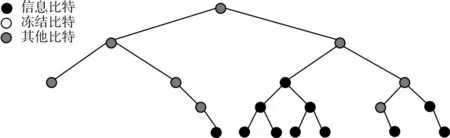
Fig.7 SCL decoding pruning freeze BIT图7 SCL 译码剪枝冻结比特


Fig.8 SCL decoding algorithm final optimized binary tree图8 SCL 译码算法最终优化二叉树
算法优化主要是对二叉树所需遍历的节点进行缩减,以减少遍历过程中需要运行的节点数,通过这种优化的剪枝PB-SCL 方法可以显著降低极化码SCL 译码算法复杂度且不损失传统SCL 译码算法的性能。
4 仿真结果与分析
基于MATLAB R2018b 仿真平台,在AWGN(加性高斯白噪声)信道下,取码长N=256,码率为0.5,进行极化码仿真。选用列表搜索宽度L=8 进行译码,采用CRC-16 将D16+D15+D2+1 作为生成多项式。如图9 所示,横坐标为信噪比(彩图扫OSID 码可见),纵坐标分别为误码率和误帧率。结果表明,SC 译码算法在进行译码时性能要低于其他几种译码算法性能,因为SC 译码算法在译码过程中如果对其中一个比特进行了错误判决,将会导致整条译码路径错误。因此级联了CRC 的CA-SCL 译码算法由于搜索宽度的增加而对译码路径存在较高的容错率,则译码性能较SC 译码算法得到提升。优化的剪枝PB-SCL 译码算法与传统SCL译码算法译码性能相当,但通过剪枝的方法减少了需要遍历的总节点数,传统SCL译码算法的机器运行时间为16 217.6s,优化的剪枝PB-SCL 译码算法机器运行时间为12 407.14s,较传统的SCL 译码算法而言降低了译码算法复杂度。

Fig.9 Performance simulation of polarization code decoding algorithm图9 极化码译码算法性能仿真
5 结语
极化码是可以达到香农信道容量的编码方式,SC 译码算法在码长趋于无穷大时会达到信道容量,但是由于SC 译码算法存在局限性,容错率较低。鉴于此,本文提出SCL 译码算法,虽然随着L 搜索宽度增加译码性能得到提升,但译码复杂度也随之增加。本文对极化码的编译码原理作详细介绍与解析,引入优化的剪枝PB-SCL 译码算法,并对几种译码算法进行仿真分析。结果表明,SC 译码算法性能在中短码长情况下的性能要低于其他几种译码算法性能,加入了循环冗余校验的CA-SCL 译码算法性能得到提高[21]。优化后的剪枝PB-SCL 译码算法以较低的译码复杂度获得了与传统SCL 译码算法相当的性能。因此,在不损失译码性能的情况下,降低译码复杂度和解码时延需作进一步研究,以便其能更好地应用于现实生活中。

