PCA 算法在银屑病BP 神经网络建模中的应用研究

詹秀菊

（广州中医药大学医学信息工程学院，广州510006）

0 引言

银屑病是一种多因素的慢性炎症性疾病，病程较长，有易复发倾向，有的病例几乎终生不愈。据报告，我国目前银屑病患病率为0.4%，估计有600 余万患者，欧美国家发病率高于黄种人和黑种人[1]，欧洲的患病率为2%-3%[2]。该病发病以青壮年为主，对患者的身体健康和精神状况影响较大。临床表现以红斑、鳞屑为主，全身均可发病，以头皮、四肢伸侧较为常见，多在冬季加重，导致患者出现身体形象以及心理的问题，进而影响患者的正常生活[3]。

英国统计学家卡皮·皮尔逊提出的PCA 算法将多指标化为少数综合指标的一种统计分析方法[4]。其基本思想是将原有较多变量线性组合转变为少数新变量来压缩原有数据矩阵的规模，进而从高维属性中挖掘出含有信息量最大的影响因子，揭示事物的本质[5]。本研究主要利用PCA 算法将输入变量降维，用较少的计算量来选择变量，获取最佳变量子集合，从而减少BP神经网络预测模型的运行时间。

1 PCA算法运行步骤

PCA 算法具体步骤如下：

（1）构建样本矩阵为X={x1,x2,x3,…xn}，其中n 表示样本矩阵的列数，每一列数据代表一个样本维度。

（2）构建协方矩阵：

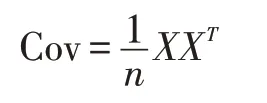
（3）计算协方矩阵Cov 的特征值和特征向量，将特征值按照单调递减排序λ1≥λ2≥λ3…λn，与之对应的特征向量为w1,w2,w3…wn。

（4）选取前k 个特征向量组成矩阵w。

（5）求取主成分Z。

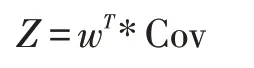
（6）计算主成分贡献率以及累计贡献率。

一般选取累计贡献率达到85%以上的主成分因子作为样本判别的主要影响因子，作为输入变量。

2 数据的采集与清洗

（1）文献数据的采集

将文献中的文献题目、发表时间、第一作者、证型、中医症状、收录范围、期刊名称以及治疗方法等信息复制到Excel 2016 工作表中，如图1 所示。

图1 文献信息表

（2）症状变量选取

选取与银屑病相关的皮损症状、全身症状、舌象以及脉象症状指标作为输入变量，其中皮损症状有皮疹发展迅速、皮疹经久不退、皮疹消退、皮损鲜红（红）、皮损淡红、皮损暗红、点滴状皮疹、斑片状皮疹、地图状皮疹、鳞屑干燥脱落、鳞屑附着紧、皮损肥厚、浸润明显、皮肤干燥、皮肤潮湿、皮损灼热和皮损肿胀等17 个症状，全身症状有疲乏、咽干、咽燥、咽肿、咽喉痛、肢体倦怠、头晕、胸闷、纳呆、喜冷饮、口干、口渴、口苦、失眠多梦、不寐、心烦易怒、便干、便秘、便溏、小便黄赤和唇青紫等21 个症状，舌象有舌红、舌紫暗、舌暗红、舌淡红、瘀斑、苔黄、苔白、苔薄、少苔、舌燥和苔腻等11 个症状，脉象有浮脉、沉脉、缓脉、数脉、涩脉、滑脉、弦脉、细脉和濡脉等9 个症状。

（3）证型变量选取

赵炳南老中医将银屑病分为血热型、血燥型、血瘀型三型辨证治疗，朱仁康认为银屑病可分为血热型、血燥型、风湿型、毒热型[6]。周鸣岐等根据银屑病的病例特点将其分为风热血热与风热血燥两型[7]。本研究证型的选取参考《寻常型银屑病（白疕）中医药临床循证实践指南2013 版》[8]，选取血热型、血燥型、血瘀型等三型为输出变量。

（4）数据归一化处理

数据挖掘的前提是数据归一化处理，其目的在于将文献数据转变为数值类型的数据，有利于机器识别。本研究中自变量X 为症状信息，X1，X2，X3，…，X58 分别代表58 个症状变量。因变量Y 为证型信息，即Y 代表证型。其中症状有无分别设置为1、0，血燥型、血瘀型、血热型分别设置为1、2、3，并录入到Excel 2016 工作表中，如表1 所示。

表1 数据量化表

本研究筛选符合条件的文献共445 篇，每篇文献录入一条病案，即录入Excel 文件中病案共445 条。其中输入变量有皮损症状、全身症状、舌象和脉象等58个症状，输出变量为血燥型、血瘀型、血热型。

3 PCA降维

（1）数据准备将银屑病数据保存为名为sheji1.xls 的Excel 文件，利用MATLAB 2015a 软件中xlsread（）函数读取数据，将读取的数据命名为data1，读取data1 中1 到58列作为输入数据命名为input，读取data1 中第59 列数据作为输出数据命名为output。具体代码如下：

（2）算法参数设定

PCA 算法的累计贡献率变化对BP 神经网络性能具有一定的影响，为了准确、迅速地选取累计贡献率，PCA 算法的累计贡献率在80%到100%之间选取。本研究利用MATLAB 2015a 自带工具箱实现PCA 降维的功能，代码如下所示，以BP 神经网络预测模型的准确率及运行的时间为判断指标，比较BP 神经网络与PCA-BP 神经网络的准确率、时间，选取PCA 参数最合适的累计贡献率。

实现PCA 模型参数设定的核心代码如下：

如图2 所示，从图形上可看出，PCA-BP 神经网络模型的运行时间大部分是小于BP 神经网络模型的运行时间，除了当累计贡献率为0.95 时，该累计贡献率可删除，不选取该值作为PCA 算法的参数值，整体结果可说明PCA 算法能够减少BP 神经网络运行时间。当累计贡献率为0.83、0.84、0.85、0.86、0.88、0.90、0.93、0.94、0.96、1 时，PCA-BP 神经网络模型的准确率大于BP 神经网络模型的准确率，收集以上符合条件的累计贡献率汇总为一个表，如表2 所示，从表中可看出准确率排名前五的累计贡献率有0.83、0.85、0.88、0.84、0.93，其相对应的准确率分别为0.92、0.90、0.86、0.86、0.85。PCA-BP 神经网络模型运行的时间排名前五的累计贡献率有0.93、0.90、0.85、0.88、0.84，其对应的运行时间分别为0.78、0.88、0.95、0.98、1.03。综合各种因素考虑，PCA 的累计贡献率设置为0.93，PCA-BP 运行时间为0.78，准确率为0.85。

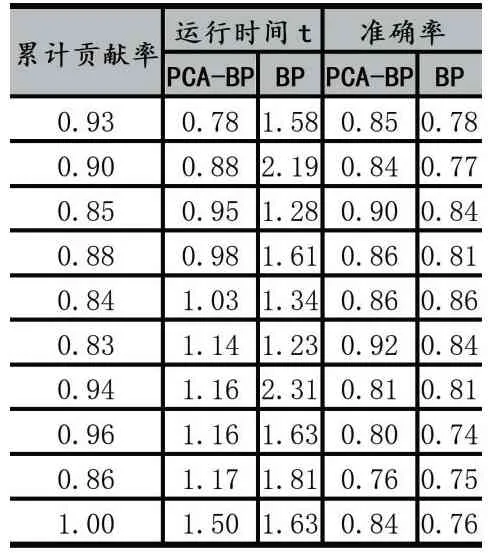
表2 累计贡献率表

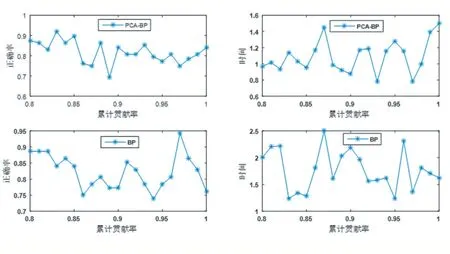
图2 PCA参数运行图

（3）结果分析

PCA 模型根据上面可确定累计贡献率设置为0.93，运行以下代码，可得出各个因子的贡献率以及累计贡献率，且各因子的贡献率按降序排列，如表3 所示，从表中可看出第34 个主成分因子的累计贡献率为0.9267，第35 个主成分因子的累计贡献率为0.9329，因累计贡献率参数设置为0.93，即提取前面34 个主成分因子作为BP 神经网络模型的输入变量。

实现PCA 降维的代码如下：

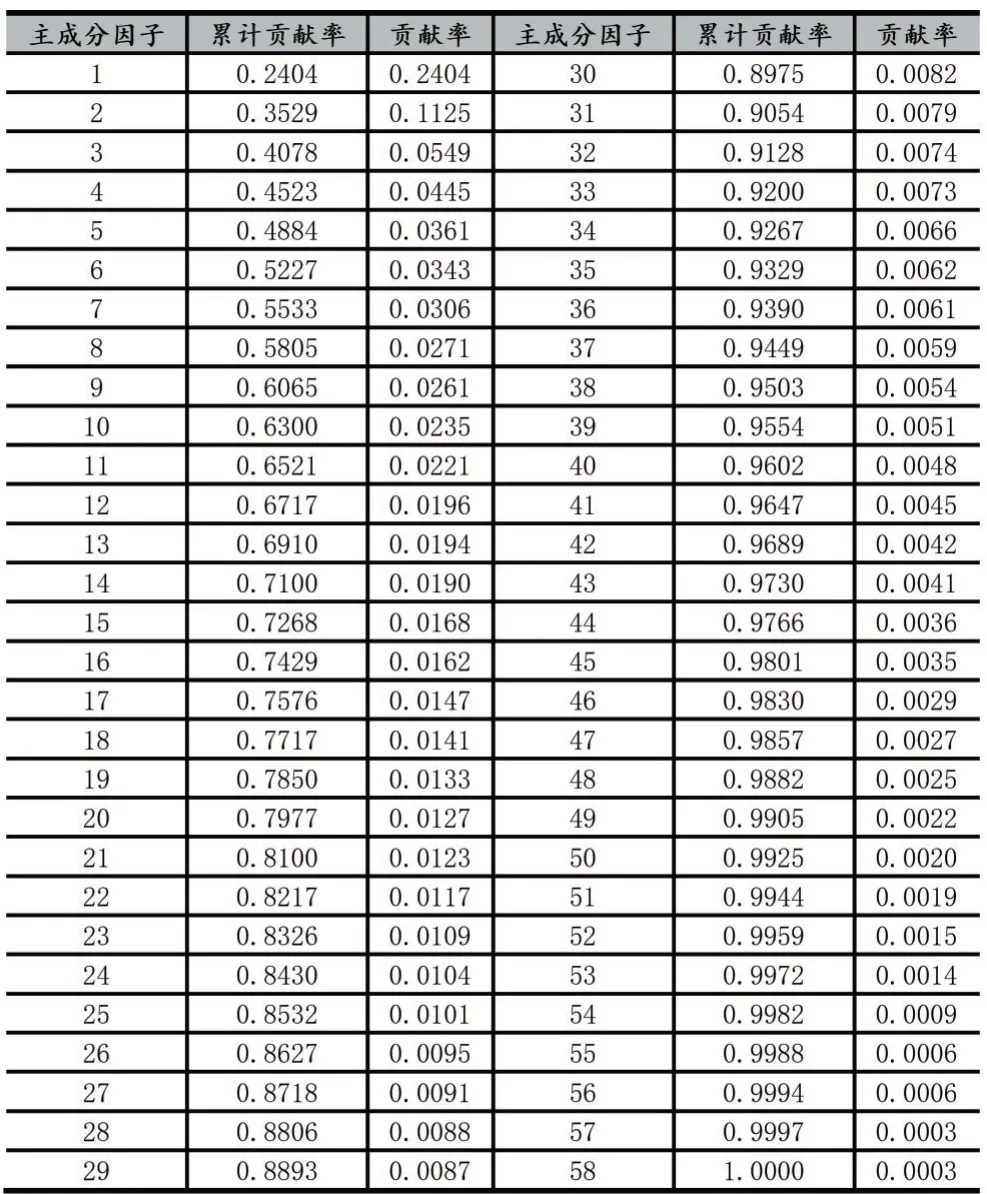
表3 主成分因子贡献率

综上所述，PCA 算法具有提取决定性作用指标的特性，以减少计算工作量。本研究PCA 算法的累计贡献率设置为93%，将58 个症状输入变量变成34 个主成分因子，以减少BP 神经网络预测模型的运行时间，实验结果也证明PCA 算法具有消除冗余的特征，减少了银屑病BP 神经网络预测模型运行时间，提高模型的运行效率。