不确定时滞神经网络鲁棒采样同步控制研究
张赣雷,王春柱,谢立典,王嘉伟,葛超
(1.华北理工大学人工智能学院,唐山063200;2.火箭军综合训练基地学兵训练一队,唐山064000;3.石家庄海山实业发展总公司,石家庄050200)
0 引言
在研究神经网络这一典型非线性系统中,人们发现时延是一个不容忽视的问题,它会影响系统的动力学行为。已有的研究大致可以划分为两类,带时延和不带时延。显然,带时延的研究具有更低的保守性[1-3]。本文引入了两种时延,离散时延和分布式时延。
不确定性和干扰广泛存在于神经网络系统中,它们会影响系统的性能甚至造成系统的不稳定。因此,研究带有不确定性和干扰的神经网络具有重要的现实意义[4-5]。文献[4]提出了一种不确定神经网络的变结构控制方法,有效地控制住了系统中的“抖振”问题。文献[5]借助H∞最优控制方法和滑模控制理论,提出了一种针对具有执行器故障和干扰的不确定神经网络的控制方案。
本文研究了带有干扰和不确定性的时滞神经网络的鲁棒同步问题。通过构建带有时滞信息的LKF,利用新的积分不等式、舒尔补定理和凸组合技术,推导出了具有更低保守性的结果。最后利用一个仿真实验验证了所提方法的有效性。
1 问题阐述
考虑如下不确定时滞神经网络系统:


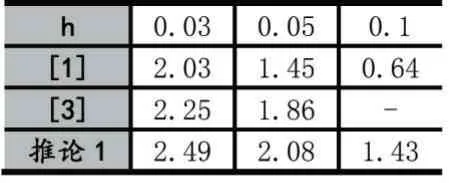
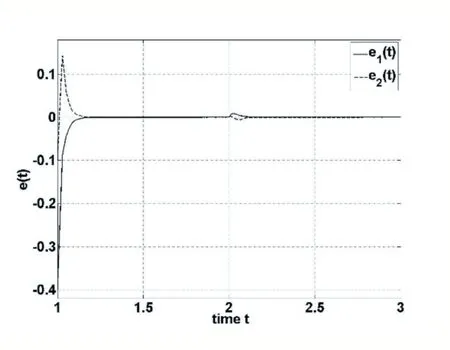
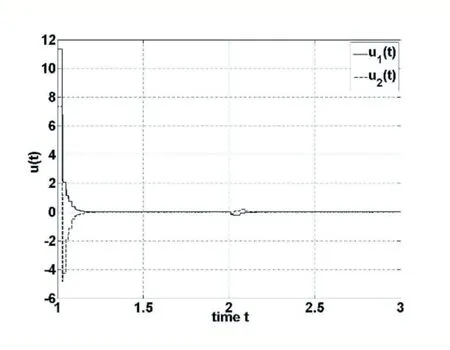
其中,tk≤t 下面给出的定理和引理将被应用于证明过程中。 定义1 给定两个正数a和b,若以下不等式成立,则系统(1)和(4)实现了指数同步,系统(6)实现了指数稳定。 对于满足FT(t)F(t)≤I条件的函数F(t) 和标量σ>0 而言,以下不等式成立: W1+σHHT+σ-1ETE<0 本部分内容将给出SES 的稳定判据,推导增益矩阵K。为了简化矩阵表述,特给出以下表述符号: 显然,主从系统实现了稳定,增益矩阵K可以通过K=G-1L求得。 本部分将对推论1 进行实验验证。 考虑具有如下参数矩阵的神经网络系统: 表1 列举了不同h 下的最大同步率α。可以看出,相较于文献[1]和[3],在相同情况下,本文提出的方法能够更快实现SES 的同步,从而例证本文列举方法的有效性。 表1 不同h 下的最大同步率α 通过求解LMIs(28)-(31),对应的控制器增益矩阵K为: 通过求得的增益矩阵K,我们可以画出误差e(t)(图1)和控制器u(t)(图2)轨迹曲线。图3 显示出误差随着时间增长趋近于零,即验证了我们方法的有效性。 图1 误差e(t) 图2 控制器u(t) 本文基于李雅普诺夫稳定性理论,通过构造新型泛函,利用新的积分不等式和凸组合技术,研究了带有干扰和不确定性的时滞神经网络的鲁棒同步问题。实验结果验证了本方法的有效性。

2 主要成果

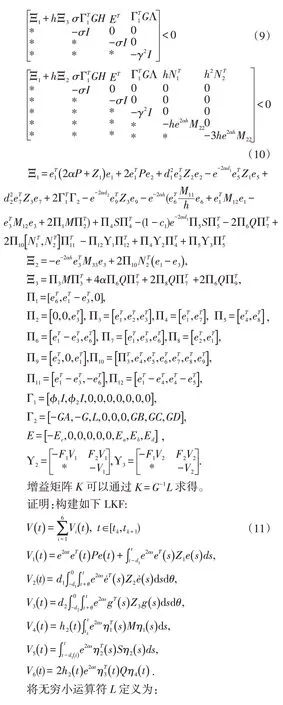


3 仿真实验

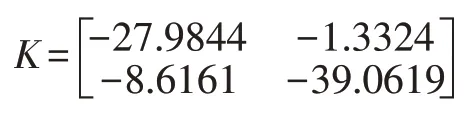
4 结语

