高阻尼隔振器对弹性梁动态特性的影响研究

沈洪兴 刘伟 漆庄平 刘海平 杨杰峰 刘会杰 张璇

摘   要：为了研究高阻尼隔振器对弹性梁动态特性的影响，分别建立单层和双层连续弹性支承梁动力学模型.在空间-频率域給出正弦稳态激励下弹性梁的动力学响应.分别定义沿弹性梁垂直方向的力传递率和水平方向的平均振动衰减率，对比高阻尼隔振器对弹性梁动态响应的控制效果.计算结果表明：相比常规线弹性支承，高阻尼隔振器可有效抑制弹性梁的力传递率幅值并增加弯曲波的空间传递衰减率;同时，梁-高阻尼隔振器系统固有频率大于梁-线弹性支承系统固有频率;通过调整高阻尼隔振器的安全系数ε和刚度比α，可优化弹性梁的力传递率和空间衰减率的有效工作频段和响应幅值.

关键词：高阻尼;隔振器;弹性梁;欧拉-伯努利梁;动态特性

Abstract：In order to analyze the influence of the hyper-damping isolator on the dynamic characteristics of elastic beam， the dynamic mechanical models of the beam on single-layer and two-layer continuous elastic foundation were presented， respectively. The dynamic responses of the elastic beam under harmonic steady excitation were given in space-frequency domain. For comparison， the definition of force transmission ratio and vibration decay rate along the vertical and horizontal direction of the elastic beam were provided， respectively. Then， the control effectiveness of the hyper-damping isolator on the dynamic characteristics of the beam on the elastic foundation was evaluated. The calculating results show that the amplitude of the transmission force rate and decay rate of the flexural wave in space domain can be enhanced by using the hyper-damping isolator when compared with the common linear elastic foundation. Besides， the system frequency of the beam with hyper-damping isolator was higher than the beam on elastic foundation. Finally， the effective working frequency range， the amplitude of the transmission force rate and the vibration decay rate of the beam can be optimized by adjusting the parameters of stiffness ratio ε and the safe coefficient α of the hyper-damping isolator.

Key words：hyper-damping;isolator;elastic beam;Euler-Bernoulli beam;dynamic characteristics

梁结构常见于轨道交通、石油化工、起重机械等工程领域，且多为金属弱阻尼结构. 因此，梁结构中产生的各类振动波可实现远距离传递且向周围环境辐射噪声. 为了有效控制弹性梁产生的振动声辐射，提高其空间振动衰减特性意义重大. 例如，通过在弹性梁上引入非连续质量或者非连续刚度，实现阻抗失配可以达到减振降噪的设计目标. Brennan等[1-2]研究了弹性梁中引入调谐振子对局部和全局梁结构简谐振动的控制效果.Thompson[3]分别对无限长弹性梁中采用单层连续弹性支承，连续动力吸振器和双层连续弹性支承等方式对梁上弯曲波传递特性的影响展开理论研究，并给出不同边界条件下实现弯曲波空间振动高效衰减的最优参数.

以轨道交通为例，钢轨作为一类典型的弹性梁结构，是轮轨振动辐射噪声的重要环节.为了抑制钢轨上弯曲波的长距离传递，开展了多种减振降噪方法和影响因素研究，如：两自由度轨道动力吸振器[4]、轨下扣件刚度频变的影响[5]、轨下支承形式的影响[6-7]、道板动力吸振器[8]等. 以上研究涉及的减振降噪方法均采用线弹性减隔振方案，其振动抑制性能存在显著缺陷，即：刚度和阻尼呈相反的变化规律，刚度增加阻尼降低，而阻尼增加刚度则被削弱;并且，刚度太小将显著影响其静态承载能力.

近年，技术人员尝试将负刚度元件插入减隔振系统[9-11]中，通过正负刚度组合使用实现阻尼放大效果且系统刚度也未被削弱，由此提出高阻尼（Hyper-damping）隔振器的概念. 为了保证系统刚度不降低，高阻尼隔振器的等效刚度与线性隔振器的刚度相同. 超阻尼是指在阻尼极低的振动系统中，在保证系统静刚度和黏性阻尼参数不变的情况下，对系统采用正负刚度组合，而表现出比原来振动系统的阻尼比高几个数量级的现象[9]. 本文保证了系统静刚度和黏性阻尼参数不变，通过对系统进行正负刚度组合，利用其正负刚度元件所产生弹性恢复力之间的相位差来获取超阻尼. 已有文献[9-11]重点研究了安装在刚性基础上单自由度高阻尼隔振器受外部力激励，在时间域和频率域的响应特性和隔振器阻尼放大效果的形成机理. 尚显不足的是，弹性结构与高阻尼隔振器的耦合作用对其减隔振性能的影响研究还未见报道.

综上，本文尝试将高阻尼隔振器替换弹性梁下的线弹性支承，并分别建立单层/双层弹性支承梁的理论模型;在空间-频率域对不同支承条件下沿彈性梁垂直方向和水平方向的振动传递特性进行研究;在此基础上，针对高阻尼隔振器的关键设计参数安全系数ε和刚度比α进行影响分析. 结果表明：高阻尼隔振器可显著提升弹性梁上弯曲波传播的空间衰减特性，并有效抑制其振动响应.

1   含高阻尼隔振器的单层弹性支承梁

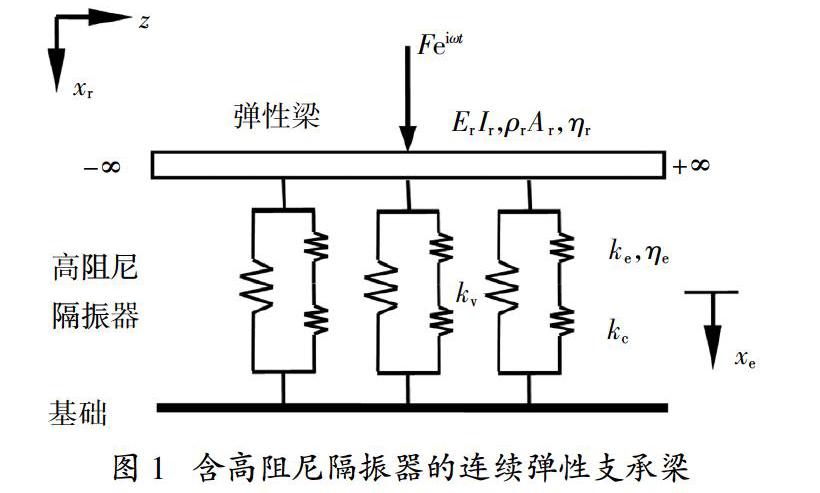
含高阻尼隔振器的单层弹性支承梁模型，如图1所示. 模型中，高阻尼隔振器简化为连续分布的弹性层;弹性梁表示为无限长欧拉-伯努利梁;所有刚度均为复刚度.

2   含高阻尼隔振器的双层弹性支承梁

图2给出含高阻尼隔振器的双层弹性支承梁模型. 与单层弹性支承梁相比（参见图1），高阻尼隔振器下串联了中间质量ms;弹性支承刚度kb和损耗因子ηb;将高阻尼隔振器替换为线弹性支承kp和损耗因子ηp，则系统模型变为常规双层线弹性支承梁.

3   数值计算及分析

以轨道交通为例，选择常见有砟轨道参数[4]作为初始设计参数，具体如下：Er = 2.1 × 1011 N/m2，ρr = 7 850 kg/m3，ηr = 0.01，Ar = 7.69 × 10-3 m2，Ir = 30.55 × 10-6 m4;ms = 270 kg/m，kb = 4.93 × 106 N/m2，ηb = 1.0;kp= 2 × 108 N/m2，ηp = 0.2;α = 3，ε = 0.05;其他参数可根据第1节给出的公式导出.以下重点讨论高阻尼隔振器设计参数对弹性支承梁动力学特性的影响.

3.1   单层弹性支承梁

图3给出不同安全系数ε对应安装高阻尼隔振器单层支承梁的力传递率曲线. 同时，为了对比还给出线弹性支承梁的力传递率曲线.由图可见，线弹性支承梁的力传递率在约300 Hz呈现一个峰值，对应梁-线弹性支承系统的固有频率;高阻尼隔振器支承梁的力传递率峰值频率均大于300 Hz，且受阻尼影响峰值随着安全系数ε增加而减小且小于线弹性支承梁的力传递率峰值;通过调整高阻尼隔振器的安全系数ε，力传递率峰值和频率均发生变化，即：安全系数ε增大，峰值频率减小，响应幅值也降低.

高阻尼隔振器的另一个关键设计参数刚度比α对弹性梁力传递率的影响，如图4所示.可见，安装高阻尼隔振器弹性梁的力传递率峰值频率均小于线弹性支承梁;而且，随着刚度比α增加，力传递率峰值降低而相应频率增大.

此外，对比图3和图4，不同支承条件和高阻尼隔振器设计参数变化，对200 Hz以内频段的力传递率幅值的影响可忽略;在低频段，力传递率呈平直段小于1说明梁下支承结构具备一定的隔振能力且平直段数值与梁下支承结构的刚度相关.并且，在约200 ～ 400 Hz频段安装高阻尼隔振器弹性梁的力传递率峰值均小于线弹性支承梁. 但是，在400 Hz以上高频段，安装高阻尼隔振器弹性梁的力传递率幅值均大于线弹性支承梁.

相比于有限尺度结构，无限长梁不存在模态特征而是表现为振动波的形式，主要包括：弯曲波、压缩波和扭转波.本文重点研究可以长距离传递弯曲波的衰减特性，引用空间平均衰减率的概念表征沿弹性梁传递的弯曲波衰减特性，即：

400 Hz以下频段的平均振动衰减率;且随着安全系数ε或者刚度比α增加，该频率范围的平均振动衰减率减小. 显然，高阻尼隔振器更利于减小弹性梁在中低频段的振动声辐射;但是，在400 Hz以上频段，高阻尼隔振器对弹性支承梁平均振动衰减率的影响可忽略.

3.2   双层弹性支承梁

高阻尼隔振器的安全系数ε和刚度比α对应双层弹性梁的力传递率曲线，如图7和图8所示. 可见，线弹性支承梁的力传递率曲线呈现两个峰值，分别对应弹性梁和中间质量在下层弹性支承上的同相位振动和弹性梁在上层弹性支承上的振动.由于高阻尼隔振器替换了上层线弹性支承，导致系统力传递率曲线主要在第二个峰值频率附近发生变化. 高阻尼隔振器支承弹性梁的力传递率第二个峰值均小于线弹性支承梁，且峰值频率向高频移动;随着安全系数ε增加，峰值减小相应频率略向低频移动;刚度比α增加，峰值减小相应频率向高频移动.

可见，高阻尼隔振器的安全系数ε和刚度比α变化可实现平均振动衰减率最大值分别约为25 dB/m和18 dB/m且相应频率向高频移动. 与单层弹性支承梁相比，高阻尼隔振器可以显著改善弯曲波在弹性梁上的振动衰减特性;但是，有效工作频段比未安装高阻尼隔振器的单层弹性梁略窄.

4   结   论

本文研究了新型高阻尼隔振器控制弹性梁振动传递特性的有效性.分别建立安装高阻尼隔振器的单层和双层弹性梁的理论模型，并定义力传递率和平均振动衰减率作为评价高阻尼隔振器减隔振性能的技术指标. 在此基础上，选择轨道交通工程领域实际的轨道结构参数（如：单层弹性支承梁为块式轨道，双层弹性支承梁为有砟轨道），相关分析结论可直接用于指导工程方案选型和设计.本文重点分析了弹性梁支承方式和高阻尼隔振器的关键设计参数安全系数ε和刚度比α变化对其减隔振性能的影响.分析计算发现：

1）安装高阻尼隔振器后单层弹性梁-支承系统的力传递率峰值得到有效抑制;安全系数ε越大，共振峰值衰减越明显，且高频响应幅值也得到一定程度降低;刚度比α越大，共振峰值也可以得到显著衰减且当α > 8时近似为无谐振峰响应，而在高频段的响应幅值则逐渐趋于一致.

2）从空间域振动波衰减特性角度，安装高阻尼隔振器可以显著提高单层弹性梁在中低频段的振动衰减性能;且取过大或者过小的刚度比α和安全系数ε均不利于提高其空间振动衰减率.

3）针对双层弹性支承梁，将上层弹性支承替换为高阻尼隔振器，在弹性梁-高阻尼隔振器系统的固有频率附近频段的力传递率和平均振动衰减特性均得到显著改善;能够带来超阻尼的弹性梁-高阻尼隔振器系统，相比于弹性梁支承系统，在系统静刚度和黏性阻尼参数一定的条件下，通过选取合适的安全系数ε和设计参数刚度比α，可以显著提高平均振动衰减特性，进而可以显著抑制弹性梁的弯曲振动响应.由于梁下支承结构刚度较大，导致高阻尼隔振器的控制效果不明显;在有效作用共振峰处，安全系数ε > 0.1和刚度比α > 8时，共振频点处近似为无谐振峰响应.

4）相比于安装高阻尼隔振器的单层弹性支承梁，安装高阻尼隔振器显著提高双层弹性支承梁空间振动衰减率. 其中，安全系数ε和刚度比α取较小值时有利于提高空间振动衰减率的峰值. 但是，有效控制频段略微变窄.

参考文献

[1]    BRENNAN M J. Control of flexural waves on a beam using a tunable vibration neutraliser[J]. Journal of Sound and Vibration，1999，222（3）：389—407.

[2]    BRENNAN M J，DAYOU J. Global control of vibration using a tunable vibration neutralizer[J]. Journal of Sound and Vibration，2000，232（3）：585—600.

[3]    THOMPSON D J. A continuous damped vibration absorber to reduce broad-band wave propagation in beams[J]. Journal of Sound and Vibration，2008，311（3/4/5）：824—842.

[4]    WU T X. On the railway track dynamics with rail vibration absorber for noise reduction[J]. Journal of Sound and Vibration，2008，309（3/4/5）：739—755.

[5]    尹镪，蔡成标，朱胜阳. 扣件刚度频变特性对轮轨振动噪声的影响[J]. 振动与冲击，2017，36（18）：231—237.

YIN Q，CAI C B，ZHU S Y.Effect of the frequency-dependent stiffness of rail fasteners on the wheel-rail vibration noise[J]. Journal of Vibration and Shock，2017，36（18）：231—237. （In Chinese）

[6]    王炯，吴天行. 浮置板轨道隔振性能研究[J]. 上海交通大学学报，2007，41（6）：1021—1025.

WANG J，WU T X. On vibration isolation performance of floating slab track[J]. Journal of Shanghai Jiao Tong University，2007，41（6）：1021—1025. （In Chinese）

[7]    LI Z G，WU T X. Modelling and analysis of force transmission in floating-slab track for railways[J]. Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2008，222（1）：45—57.

[8]   ZHU S Y，YANG J Z，CAI C B，et al. Application of dynamic vibration absorbers in designing a vibration isolation track at low-frequency domain[J]. Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2017，231（5）：546—557.

[9]   ANTONIADIS I，CHRONOPOULOS D，SPITAS V，et al. Hyper-damping properties of a stiff and stable linear oscillator with a negative stiffness element[J]. Journal of Sound and Vibration，2015，346（1）：37—52.

[10]  ANTONIADIS I A，KYRIAKOPOULOS K J，PAPADOPOULOS E G.Hyper-damping behavior of stiff and stable oscillators with embedded statically unstable stiffness elements[J]. International Journal of Structural Stability and Dynamics，2017，17（5）：1740008.

[11]  董光旭，張希农，谢石林，等. 基于负刚度机构的高刚度-超阻尼隔振器设计与研究[J]. 振动与冲击，2017，36（9）：239—246.

DONG G X，ZHANG X N，XIE S L，et al. Design of a high stiffness and hyper-damping vibration isolator based on negative stiffness mechanism[J]. Journal of Vibration and Shock，2017，36（9）：239—246. （In Chinese）