基于机液联合仿真的剪叉机构疲劳寿命分析

黄向明 张特 尹人奇 刘国良

摘   要：为解决工程机械复杂机液结构的疲劳寿命计算问题，以某型号高空作业平台剪叉机构为研究对象，提出了一种基于机液联合仿真的结构疲劳寿命计算方法.首先，建立了剪叉机构的机液联合刚柔耦合多体动力学仿真模型，分析了剪叉机构在举升过程中的受力情况，确定了极限工况为举升阶段79.2 s时刻，提取了各关键铰点处的载荷谱;并通过剪叉机构的油缸压力和结构应力测试实验，验证了动力学仿真模型的正确性;然后，基于联合仿真确定的极限工况和铰点载荷谱，对剪叉臂进行了极限工况下和单位载荷作用下的静力学分析，得到了剪叉臂结构应力分布情况;最后，利用铰点载荷谱和剪叉臂结构应力通过仿真获得剪叉臂疲劳损伤云图，确定了剪叉臂疲劳危险部位主要是剪叉臂各个零部件的连接位置处，为后续的疲劳寿命优化提供了基础.

关键词：剪叉机构;机液联合动力学仿真;刚柔耦合;载荷谱;疲劳寿命

Abstract：In order to solve the fatigue life calculation problem of engineering machinery complex machine-liquid structure， this paper proposed a calculation method for structure fatigue life based on mechanical and hydraulic co-simulation technology， taking the scissor mechanism of a scissor aerial work platform as the research object. A multi-body dynamics simulation model of mechanical-hydraulic combined rigid-flexible coupling of scissor mechanism was established， and the force status in the lifting process of scissor mechanism was also analyzed. The ultimate working status was determined at the lifting stage of 79.2 s， while the load spectrum at each key hinge point was extracted. Under the same working status of simulation， the test experiments of oil cylinder pressure and structural stress were carried out. The experimental results verified the correctness of the dynamics simulation. Then， according to the load spectrum of the hinge point and the ultimate working status confirmed by co-simulation， the static analysis of scissors arms under the ultimate working status and unit loading action was carried out to obtain the static stress distribution of scissors arms structure. Eventually， by using the hinge point load spectrum and the static stress distribution， the fatigue damage and fatigue life of scissor arms were obtained. The results confirmed that the most hazardous part of scissors arms fatigue was the connecting position of each part of scissors arms， which provided a basis for subsequent fatigue life optimization.

Key words：scissors mechanism;mechanical and hydraulic co-simulation;rigid-flexible coupling;load spectrum;fatigue life.

剪叉式高空作业平台因操作简单、运行平稳、承载和适应能力强而广泛应用于工程建设和市政维修等各个领域[1]. 剪叉机构作为剪叉式高空作业平台的关键部件，其结构的强度和疲劳性能直接关系到整个作业平台的稳定性和安全性.

目前，对于剪叉式高空作业平台剪叉机构的强度和疲劳性能的研究有：胥军等人分析了剪叉式升降平台的运动过程，校核了剪叉杆的强度，并通过调整油缸的安装位置，提高了平台运行稳定性[2];Petru等人将剪叉式高空作業平台的试验结果与动力学仿真结果进行了对比，验证了有限元仿真的合理性[3];Ren等人通过实验测试与有限元仿真相结合的方法确定了影响平台稳定性的因素主要有平台起升速度、所处地面坡度和平台上人的活动状况[4];潘权等人对剪叉式高空作业平台的剪叉臂进行了静力学分析，并利用常幅对称循环载荷曲线进行了剪叉臂疲劳寿命分析，确定了最大疲劳损伤发生在剪叉臂的铰孔附近[5]. 在这些仿真建模方法中，仿真的边界条件等参数的设置，皆为设计值，与实际值有较大的差距，会在一定程度上影响建模的精度. 此外，国内学者对于机械产品疲劳寿命分析的研究有：李源等人对弧齿锥齿轮副进行了连续动态啮合过程的仿真，研究了该型轮齿的动态啮合齿面接触和齿根弯曲疲劳性能，得出轮齿破坏主要发生在齿根受压侧的倒角区域[6];叶南海等人提出了一种基于虚拟载荷谱技术的疲劳寿命计算方法，并将计算结果和疲劳软件的计算结果进行了比较，证明了该方法的计算结果准确可靠[7-8];卿宏军等人采用传感器采集了某车型整车主要结构载荷谱，确定了车后悬架和轮胎的固有频率，以及左后轮垂直方向力载荷对结构的伪疲劳损伤值[9]. 在这些疲劳研究中，疲劳寿命的计算主要通过两种方式：一种是利用软件对机械动力学仿真结果直接进行疲劳寿命计算[6-8]，该方法适用于仿真时长短、网格规模小的模型;另一种是通过试验采集获取疲劳载荷谱，再通过软件进行疲劳寿命计算[9]，该方法获取的载荷数据可靠，但周期长、费用高.目前对于复杂的机电液系统基于机液耦合仿真获得疲劳载荷谱来进行疲劳寿命研究比较少.

针对以上问题，本文提出基于Virtual.Lab和AMESim的机械与液压联合仿真的建模方法，按照实际情况，对动力学仿真的边界条件进行了设置，既确保了提取出的疲劳分析所需载荷谱的可靠性，又节省了大量的时间与费用，为机构的强度和疲劳寿命分析结果的准确性提供了保障.

本文以某型号剪叉式高空作业平台剪叉机构为研究对象，进行了机-液联合刚柔耦合多体动力学仿真、静力学仿真和疲劳寿命分析，并对动力学仿真结果进行了实验验证，确保了下文基于动力学仿真结果所做的分析的准确性.

1   剪叉机构的动力学仿真

1.1   作业平台结构主要参数

某剪叉式高空作业平台主要由液压及控制系统、平台总成、底盘和剪叉机构等组成，如图1所示.其工作平台最大高度为16.1 m，作业最大高度为18.1 m，平台尺寸（长×宽×高）为3.75 m×1.86 m×1.1 m，可延伸长度为1.35 m，承载能力为680 kg. 剪叉机构由上下两个液压缸和五组剪叉臂及其附件组成，各组剪叉臂从下至上编号为一至五.

1.2   剪叉机构的液压系统建模

机电液一体化联合仿真技术可以利用不同领域的仿真模型，组成复杂机电液系统的仿真模型，通过仿真可以得到更接近实际的分析结果[10]. 本文所构建的剪叉机构联合仿真模型主要由液压、机构和控制模型组成，对剪叉机构在额定载荷均载和偏载作用下全速举升工况进行研究.根据高空作业平台整车的实际液压控制回路简化出的剪叉机构液压控制回路如图2所示，以此完成剪叉机构液压部分的AMESim建模.

该高空作业平台的上升、保持、下降动作依靠两个换向阀进行控制，其升降速度控制通过可调节流阀实现.根据原理图，采用AMESim对剪叉机构液压系统建立的模型如图3所示.

模型中除了液压原理图中的元器件之外，还有信号发生器和位移速度转换器等. 图3中1处和3处为来自于Motion的上下液压缸活塞杆的位移与速度信息;2处和4处为AMESim输出到Motion中上下液压缸的液压缸推力;5处、6处和7处均为AMESim控制模块中的信号发生器，三个信号发生器中预设不同的控制函数分别控制二位二通伺服阀、三位四通伺服阀和可调节流阀的线圈输入电流，进而控制各阀芯运动.

1.3   剪叉机构的刚柔耦合模型建模

由于高空作业平台机构体积和质量较大，剪叉机构的剪叉臂弹性变形较为明显.为了真实地反映剪叉机构的动态响应，故对受力情况比较恶劣的第一至第四组剪叉臂进行柔性化处理，并计算各剪叉臂模态振型和模态参与因子.

1.3.1   载荷和约束条件处理

根据剪叉机构的工作特点，将其分为均载和偏载两种工况进行载荷施加.在有限元软件中给剪叉机构各部件设定材料属性和重力加速度.额定工作载荷为680 kg，其中工作人员为6人（80 kg/人），设备工具质量为200 kg，作用于平台上方.均载加载时，工作人员自重载荷作用在平行于工作平台长度方向的中心线上;偏载加载时，工作人员的自重载荷作用位置为平行于工作平台长度方向且距边缘0.1 m的直线上.设备质量均匀作用在工作平台25%的台面上.由于本文主要针对剪叉机构的恶劣工况进行分析，故进行均载和偏载分析时，将打开工作平台两侧延伸平台，并沿着工作平台的最大长度方向添加载荷.

工作人员的手动操作力大小为400 N，作用于平台上底面向上1.1 m处，在偏载工况下，载荷方向与工作平台侧偏方向相同;在均载工况下，载荷方向与工作平台起升方向相同.根据相关标准[11]，风压取100 Pa，单个内剪叉臂迎风面和被遮挡面所受风载荷分别为112.18 N和50.48 N;单个外剪叉臂迎风面和被遮挡面所受风载荷分别为112.18 N和76.28 N;工作平台迎风面和被遮挡面所受风载荷分别为312.63 N和196.96 N;工作人员和工具所受风载荷分别为420 N和58.8 N.考虑到剪叉高空作业平台使用情况，其设备动载荷系数为1.5[12]. 对剪叉机构底座施加固定约束，对各剪叉臂长度方向施加平行于水平面的初始角度位置约束.

1.3.2   机构模型建立

首先将剪叉机构Pro/E装配体模型进行简化后导入到多体动力学分析模块Motion中.在Motion中对剪叉机构进行运动副创建（液压缸活塞与缸体之间的圆柱副，滑块与导轨槽之间的移动副，剪叉臂与相连铰轴之间、液压缸与液压缸安装支座之间、限位连杆与连杆铰轴之间的转动副）.载荷和约束条件施加，定義活塞杆与液压缸之间的相对位移和相对速度为机构模型的输出变量，来自AMESim中的液压驱动力为机构模型的输入变量，完成剪叉机构刚体模型的创建.

考虑到举升过程中剪叉臂的变形影响，对受力情况比较恶劣的第一至第四组剪叉臂进行柔性化处理，即通过Hypermesh软件，划分各剪叉臂有限元网格模型，导入Motion柔性化分析模块Motion_Flexible body design，设置材料相关参数.同时在Motion中，刚体和柔性体之间的连接通过设置接附点（Interface Set）完成，设置好接附点后，通过替代的方法，将原来的剪叉臂刚体模型替换为柔性体模型，计算柔性化后的各剪叉臂模态数据，手动设置模态工况，过滤掉前六阶刚体模态和一些高阶模态.完成刚柔耦合建模的剪叉机构如图4所示.

1.3.3   联合仿真接口及求解设置

分别搭建好模型后，将液压模型和控制模型直接通过AMESim软件内部的信号通道进行连接，将机构模型和液压模型通过创建软件接口进行连接，从而完成剪叉机构联合仿真建模.机构和液压系统之间的变量交换如图5所示.在Motion中选择求解算法为AMESIM_COUPLED，并根据高空作业平台实际举升以及平稳状态的时间，设置求解时间为90 s，求解步长为0.01 s.

1.4   仿真结果分析

极限偏载工况为举升过程中的危险工况，故以此为例对仿真结果进行分析.

1.4.1   强度分析结果

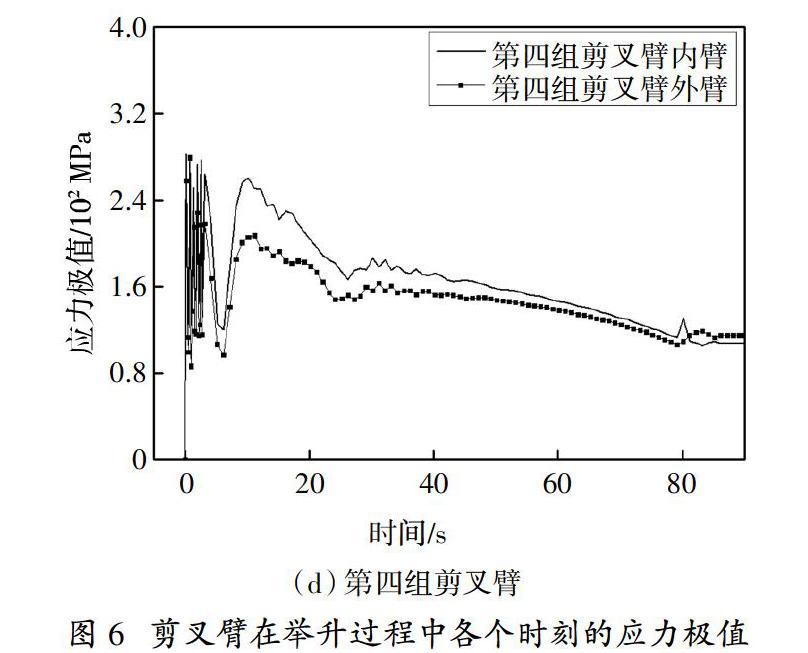
对各柔性体进行线性叠加工况分析，求解出剪叉机构在举升过程中柔性体各个时刻的应力分布情况. 提取出柔性化后的各剪叉臂在举升过程中各个时刻的应力极值，如图6所示，其中80 s时刻后各剪叉臂内臂应力处于稳定的状态.

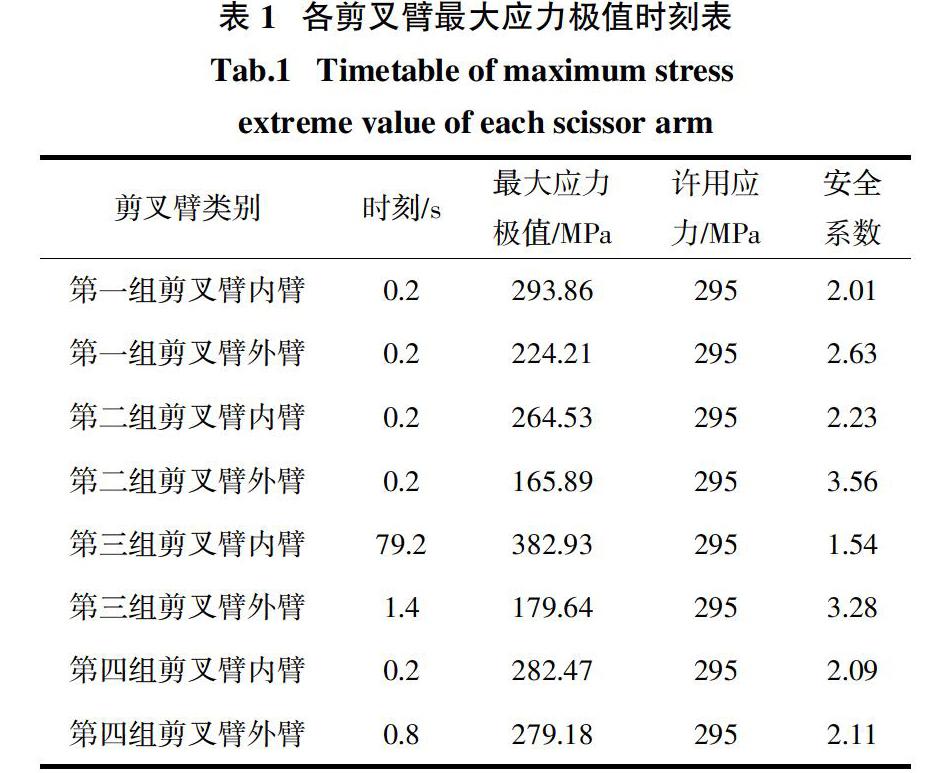
剪叉臂的材料为HG70钢，其材料屈服极限为590 MPa，根据高空作业平台设计标准要求GB/T 25849—2010，取安全系数为2.0，则许用应力为295 MPa.因此，需要计算各臂在加载过程中最大应力点及对应的时刻.由图6可得到各剪叉臂最大应力极值时刻，如表1所示. 从表1可以看出，除第三组剪叉臂内臂（内臂三）外，其余各剪叉臂的安全系数均超过了2.0，满足了强度要求. 内臂三在79.2 s时最大应力382.93 MPa，为整个臂的最大应力，此时为极限工况，其安全系数为1.54，现提取内臂三的应力分布图，对其进行强度分析如图7所示.

从图7可知，应力集中主要发生在剪叉臂各个零部件的连接位置处，其中最大应力出现在沿偏载方向的下液压缸安装肋板与方形肋管的连接处，如图中标记的圆圈处，由此可知，内臂三结构存在不合理性，需要对其结构做优化处理，以降低应力集中.

1.4.2   节点载荷谱提取

联合仿真完成以后，可以提取各关键节点的载荷谱作为疲劳分析的数据输入. 以内臂三为例，该内臂与剪叉机构其它零部件的连接点共有8个，也就需要提取8个节点的载荷谱，每一个节点都有六个通道（XYZ方向的力和力矩），总共提取了48个通道的载荷谱.

2   测试试验验证

为验证动力学仿真的准确性，对剪叉机构进行均载下液压缸压力测试和结构应力测试，并对额定载荷均载工况的仿真模拟值和实验测试值进行对比研究.

2.1   液压缸进油口压力测试

在两液压缸进油口处安装压力表，测量剪叉机构在举升过程中液压缸进油口处的油压.额定均载工况下，剪叉机构举升阶段的液压缸进油口油压仿真模拟值和试验测试值结果对比如图8所示.

从图8中可知，在平台举升过程中，液压缸进油口油压仿真模拟值和试验测试值变化一致，仿真模拟值略大于试验测试值，这是由于仿真模拟时对载荷添加了1.5倍动载系数，二者之間最大绝对误差为0.89 MPa，最大相对误差为6.38%，小于10%，在误差允许范围内.

2.2   结构应力测试

额定均载工况下，在剪叉臂上选取合适测点，重复多次进行应力测试实验.测点选择应遵循以下几个原则：1）选择结构平整、应变梯度小的区域;2）避开轴孔、焊缝等容易产生应力集中的部位;3）应方便贴片、接线等操作. 以内臂三为例，其上布置有6号至10号测点，测点分布如图9所示.

根据t检验准则对实验数据进行处理，选取相同测点下的实验测试值和仿真模拟值进行对比，二者的对比结果如图10所示[13]. 从图中可以看出，各个测点的仿真模拟值和实验测试值的变化趋势一致，大部分测点的仿真模拟值和实验测试值的绝对误差在10 MPa以内，二者相对误差均在10%以内，验证了本文所建立的剪叉机构动力学仿真模型的正确性，确保了下文基于动力学仿真结果所做分析的准确性.

3   静力学分析

为进一步验证动力学仿真的准确性，并获得疲劳分析所需要的剪叉臂结构静态分析结果，利用在Hypermesh中建立的更高精度的剪叉臂网格模型，应用惯性释放原理在ANSYS软件中对剪叉臂进行了极限工况下（偏载工况下）和单位载荷作用下的静力学分析.限于篇幅，这里仅以受力情况最复杂的内臂三为例进行说明[14-15].

3.1   有限元网格划分

内臂三网格采用8节点六面体单元，其第三组剪叉臂内臂结构件网格总数为2 940 968，节点总数为3 028 396，具体如图11所示.

3.2   极限工况静力学分析

由动力学仿真结果可知，在79.2 s时，内臂三出现最大应力极值，对该时刻进行载荷和边界条件数据提取.在ANSYS软件中利用Hypermesh生成的剪叉臂网格和上文提取的79.2 s时的载荷和边界条件数据，进行静力学分析，可得到第三组剪叉臂内臂在产生最大应力极值时刻的应力分布云图，如图12所示.

从图12可知，应力集中主要发生在剪叉臂各个零部件的连接位置处，其中最大应力出现在沿偏载方向的下液压缸安装肋板与方形肋管的连接处，最大应力为361.91 MPa，其余位置的应力均小于许用应力，达到了2倍的安全系数. 对比动力学分析结果图7和图8，剪叉臂上应力分布趋势相同，产生最大应力的位置也相同，静力学分析得到的最大应力为361.91 MPa，动力学分析得到的最大应力为382.93 MPa，两者的绝对误差为21.02 MPa，相对误差为5.5%，仿真结果基本吻合，进一步验证了动力学仿真结果的准确性.

3.3   单位载荷作用下的静力学分析

为了给疲劳寿命计算提供应力结果，现对剪叉臂进行单位载荷作用下的静力学分析.内臂三与剪叉机构中的其它零部件之间共有8个连接点，对于每个连接点X、Y、Z三个方向加载1 N的力，每一个载荷都是一个独立的计算工况，共48个工况，对应动力学分析中提取的48个载荷谱.

4   疲劳寿命分析

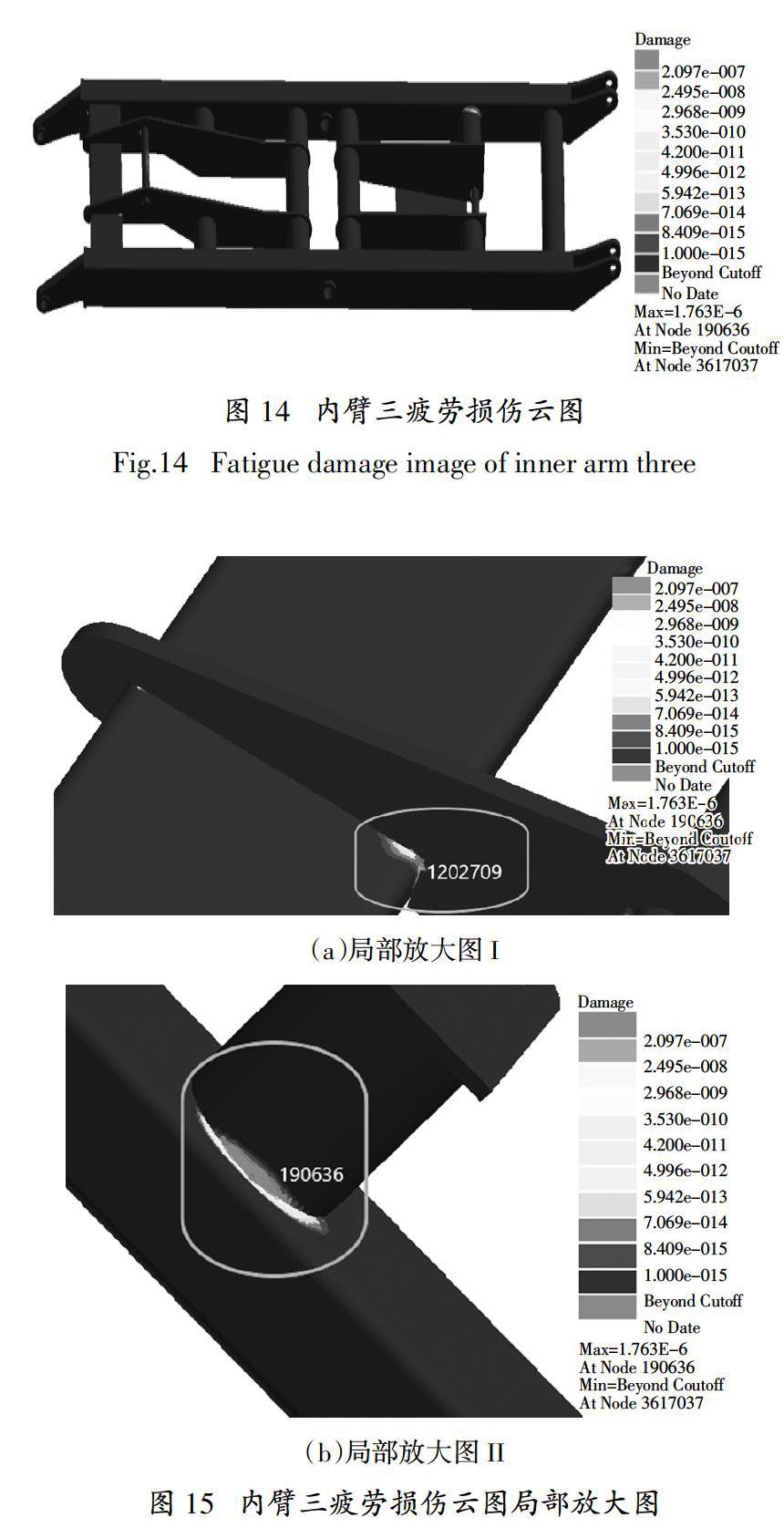
在nCode软件中，使用自定义材料曲线，拟合出的材料S-N曲线如图13所示. 利用动力学分析获得的载荷谱和静力学分析获得的应力结果，对剪叉臂进行疲劳寿命分析，可得到剪叉臂在剪叉机构的整个运动过程中各节点单元的疲劳寿命[16].以内臂三为例，计算得到的疲劳损伤云图和损伤云图的局部放大图分别如图14和图15所示.

从图可以看出，疲劳危险部位主要发生在剪叉臂各个零部件的连接位置处，其中疲劳损伤最严重的两个部位分别为下液压缸安装肋板与方形肋管的连接处和连接上液压缸安装肋板的短肋管与剪叉臂管的连接处，位置分别如图15（a）和图15（b）所示.两位置的疲劳损伤值最大的节点编号分别为1 202 709和190 636，疲劳损伤值分别为1.02 × 10-6和1.76 × 10-6，其中节点190 636也是整个剪叉臂的疲劳最危险点.此外，剪叉臂的绝大部分位置都达到了无限寿命.

假定剪叉机构的剪叉臂在下降的极限工况中所产生的疲劳损伤与举升的极限工况所产生疲劳损伤相同，则可以通过上述方法计算出内臂三在一个完整的升降过程中所产生的疲劳损伤值为3.52×10-6.假设工作平台每日的升降次数为50次，一年的工作天数按365天计算，则剪叉机构的使用寿命可以达到15.56年.剪叉机构的设计寿命为20年，由此可知，剪叉机构的剪叉臂局部位置未满足疲劳寿命要求，需要对局部位置进行结构优化.

5   结   论

1）采用机-液联合仿真的方法完成了剪叉机构

的刚柔耦合多体动力学仿真，根据仿真结果，进行了剪叉臂的强度分析以及节点载荷谱的提取，确定了剪叉臂的最危险工况发生在举升阶段79.2 s时刻.

2）对剪叉机构进行了液压缸压力测试和结构应力测试，并将实验测试值与仿真模拟值进行了对比，验证了动力学仿真分析的正确性，确保了基于动力学仿真结果的分析及优化的合理性.

3）基于动力学仿真结果，通过Hypermesh建立高精度网格模型，对剪叉臂进行了极限工况下和单位载荷作用下的静力学分析，获得了疲劳分析所需要的剪叉臂结构静态分析结果，并对剪叉臂进行了疲劳寿命分析，确定了剪叉臂发生最大疲劳损伤的部位，为后续剪叉臂结构优化提供了基础.

参考文献

[1]    牛文欢，张进生，王志，等. 现代高空作业平台的发展概况与趋势[J]. 建设机械技术与管理，2013，26（2）：97—100.

NIU W H，ZHANG J S，WANG Z，et al. Development status and trend of the modern aerial work platform[J]. Construction Machinery Technology & Management，2013，26（2）：97—100.（In Chinese）

[2]    胥軍，李刚炎，杨飞，等. 剪叉式升降机举升机构分析与优化[J].机械科学与技术，2013，32（6）：919—922.

XU J，LI G Y，YANG F，et al. Analysis and optimization for lifting mechanism of scissor-fork lifter[J]. Mechanical Science and Technology for Aerospace Engineering，2013，32（6）：919—922.（In Chinese）

[3]    PETRU M，SEVCIK L，MASIN I，et al. Dynamic analysis of lifting platform construction for car relocation[J]. Modern Methods of Construction Design，2014，8：517—524.

[4]    REN G D，CHRISTOPHER S P，JARED J H，et al. An investigation on the dynamic stability of scissor lift[J]. Open Journal of Safety Science and Technology，2012，2（1）：8—15.

[5]    潘权，张哲，贺尚红，等. 剪叉式高空作业平台剪叉臂疲劳寿命分析及预测[J]. 食品与机械，2017，33（5）：119—124.

PAN Q，ZHANG Z，HE S H，et al. Fatigue life analysis and forecast of scissors arms in scissors aerial work platform[J]. Food & Machinery，2017，33（5）：119—124. （In Chinese）

[6]    李源，韩旭，叶南海，等. 减速器弧齿锥齿轮动态啮合疲劳强度研究[J]. 湖南大学学报（自然科学版），2010，37（6）：32—35.

LI Y，HAN X，YE N H，et al. Study of the fatigue strength of the dynamic meshing of the spiral bevel gears of reducer[J]. Journal of Hunan University （Natural Sciences），2010，37（6）：32—35.（In Chinese）

[7]    叶南海，陈凯，戚一男，等. 基于虚拟载荷谱技术的锥齿轮疲劳寿命分析[J]. 湖南大学学报（自然科学版），2012，39（3）：38—42.

YE N H，CHEN K，QI Y N，et al. Fatigue life analysis of bevel gear based on virtual load spectrum[J]. Journal of Hunan University （Natural Sciences），2012，39（3）：38—42. （In Chinese）

[8]    叶南海，邓鑫，何韵，等. 谐波柔轮力学分析与疲劳寿命研究[J].湖南大学学报（自然科学版），2018，45（2）：18—22.

YE N H，DEN X，HE Y，et al. Study on mechanical analysis and fatigue life of harmonic flexspline[J]. Journal of Hunan University（Natural Sciences），2018，45 （2）：18—22. （In Chinese）

[9]    卿宏軍，韩旭，陈志夫，等. 某轿车结构载荷谱采集与分析[J]. 湖南大学学报（自然科学版），2012，39（12）：32—36.

QING H J，HAN X，CHEN Z F，et al. Acquisition and analysis of  loading spectral of a car structure[J]. Journal of Hunan University（Natural Sciences），2012，39（12）：32—36. （In Chinese）

[10]  熊伟，陈晶晶，关广丰，等. 基于VL Motion和AMESim的液压六自由度平台联合仿真及试验研究[J]. 液压与气动，2015（3）：11—14.

XIONG W，CHEN J J，GUAN G F，et al. Experiment and Co-simulation based on VL motion and AMESim for hydraulic Stewart platform[J]. Chinese Hydraulics & Pneumatics，2015（3）：11—14.（In Chinese）

[11]  Crane wind assessment： ISO 4302—1981[S]. London： International Organization for Standardization，1981：5—6.

[12]  剪叉式高空作业平台：JG-T 5100—1998[S]. 北京：中华人民共和国建设部，1998：6—10.

Scissor aerial work platform： JG-T5100-1998[S]. Beijing： Ministry of Construction of the Peoples Republic of China，1998：6-10. （In Chinese）

[13]  腾敏康.实验误差与数据处理[M].南京：南京大学出版社，2009：10—25.

TENG M K. Experimental error and data processing[M]. Nanjing：Nanjing University Press，2009：10—25. （In Chinese）

[14]  王阳，罗宇，陈震，等. 惯性释放法在大型复杂结构焊接变形预测中的应用[J]. 船舶力学，2016，20（9）：1147—1159.

WANG Y，LUO Y，CHEN Z，et al. Application of inertia relief in the prediction of welding deformation for large complex structures[J]. Journal of Ship Mechanics，2016，20（9）：1147—1159. （In Chinese）

[15]  MA J，XUE C J，DENG Y Q，et al. Optimization method of multi-body structure based on the fatigue life[C]//Proc SPIE 7375，ICEM 2008：International Conference on Experimental Mechanics 2008. 2009，7375：737514.

[16]  ZHU S H，XIAO Z J，LI X Y. Vehicle frame fatigue life prediction based on finite element and multi-body dynamic[J]. Applied Mechanics & Materials，2011，141（1）：578—585.