促进理解和迁移的四边形单元教学设计

杨小丽

(北京教育学院数学系 100044)

理解意味着能够智慧地和有效地应用与迁移[1].迁移是把一个情境中学到的东西迁移到新情境的能力[2].然而学习只有在学生达到迁移水平时才算完成[3].学生的迁移能力是学习的一个重要标志，它能帮助教师评估和改进教学[4].

四边形的课程内容应聚焦平行四边形[5].常见的平行四边形教学安排是：直接给出或回顾小学定义，分别探索并证明性质定理1，2，3，分别探索并证明判定定理1，2，3.这样的过程缺乏探索一个图形的整体性，割裂了定义、性质、判定间的内在联系，使原来在内涵、思想方法上具有一致性和连贯性的内容被人为切割，导致数学知识的碎片化[6]；不仅不利于理解平行四边形的性质，而且也不利于迁移，面对一个新图形, 如果没有了老师预先设计好的情境, 学生将很难独立开展研究.

有学者和教师从整体性的角度，对平行四边形的教学进行了改进.他们的做法是将平行四边形的教学过程调整为：给出平行四边形定义、整体探索平行四边形的性质、整体探索平行四边形的判定.这样的教学设计体现了单元的思想，有利于学生掌握研究一个图形的基本路径和思想方法，积累研究图形的活动经验.不足的是，上述整体设计对平行四边形的定义、性质和判定之间的关系揭示得不够深入，这在一定程度上会导致学生对三者之间的内在联系理解得不够充分，因而不利于迁移.

本文在学生调研的基础上，从促进理解和迁移的角度，在大观念的指引下，对四边形单元的教学进行再探索.

1 大观念是理解的核心、迁移的关键

大观念，英文Big Ideas，也有学者将其译为大概念、一般观念、核心观点.在教育领域，有关大观念的研究至少可以追溯到布鲁纳对于教育过程的研究[7].林恩·埃里克森认为大观念是指向学科中的核心概念，是基于事实基础上抽象出来的深层次的、可迁移的概念[8].格兰特·威金斯和杰伊·麦克泰格提到，大观念通常表现为一个有用的概念、主题、有争议的结论或观点、悖论、理论、基本假设、反复出现的问题、理解或原则，它能够将离散的事实和技能有意义地连结起来，是重要的、持久的、可迁移的[9].兰德尔·查尔斯将大观念定义为是对一个观念的陈述，这个观念是数学学习的核心，且能把各种数学理解联系成一个连贯的整体[10].

很多学者都提到过大观念的重要性.如，威金斯用魔术贴、锚点、车辖、透镜等来形容大观念的核心位置和关键作用.他认为，大观念相当于一个车辖，车辖是一种配件，能够使车轮固定在车轴上，因此，车辖是理解的必要条件[11].大观念照亮了经验之路，是迁移应用的关键[12].而布鲁纳也早就指出：任何学习表现的首要目标(不考虑它可能会给我们带来的快乐)，都是它应该在将来为我们服务……本质上讲，它在于学习最初并不是一种技能而是一种普通的观点.这种观点认为，它可以作为用于识别后续问题的基础.这种类型的迁移是教育过程的核心——知识的持续扩张与加深就是依据的这一观点[13].

2 促进理解和迁移的四边形整体设计

威金斯提出了理解为先的单元教学设计模式，该模式的主要目的是发展和深化学生的理解，即通过大观念理解学习内容并将学习结果进行迁移[14].笔者参照该模式，对四边形单元进行整体设计.

2.1 确定大观念及单元具体观念

兰德尔·查尔斯系统提出了21条数学大观念，其中几何领域的大观念有4条，能指引四边形单元教学的大观念是“形状和立体图形：二维和三维物体(无论是否有曲面)都可以通过其特征进行描述、分类和分析”[15]. John A. Van de Walle等也提出了几何领域的4条大观念，其中有两条能指引四边形单元教学，它们是：(1)根据图形的几何性质可以判断不同图形是否相同，图形可以根据其性质进行分类；(2)当一个图形在平面内或空间中移动时，变换提供了一种判断图形的性质是否变化的重要方法，这些变换包括平移、反射、旋转等[16].

“图形的性质”是初中图形与几何领域的重要内容，这部分内容可以体现如下数学大观念：(1)图形是从现实空间中抽象出来的；(2)图形的组成元素决定了图形的性质，可以根据图形的性质对图形进行描述、分类和分析；(3)研究图形的过程和方法包括通过抽象得到图形；通过定义表述图形；通过观察、操作、度量、归纳、类比等方法发现图形的性质；利用演绎推理从定义、基本事实、定理出发对发现的结论进行证明，从而得到图形的性质；根据图形的定义和性质，得到图形的判定.

将上述大观念具体化，得到四边形单元的具体观念：(1)四边形是从现实空间中抽象出来的；(2)四边形可以根据其边和角的特征来描述、分类和命名；(3)四边形可以由三角形构成或分解成三角形；(4)分类是认识图形特征的重要方法，也是理解图形间关系的重要手段；(5)定义是探索图形性质和判定的出发点，图形有多种定义方式，所有充分必要的性质命题都可以用“性质”构成图形的定义[17]；(6)图形的性质是指图形的整体特征(稳定性、对称性)以及图形各几何元素之间确定的位置关系、大小关系；(7)观察、操作、度量、归纳、类比、推理都是研究图形性质的有效方法；(8)图形的判定是指能够判断一个图形是否为某类图形的条件；(9)图形的性质定理和判定定理一般是互逆的关系，可以通过性质定理的逆命题寻找图形的判定定理，也可以将图形的性质罗列出来，将性质两两组合构造命题，如果命题为真，则可以作为图形的判定定理；(10)经过合情推理发现的结论不一定正确，通过演绎推理可以证明一个命题是正确的，利用反例可以判断一个命题是错误的；(11)图形变换既是研究图形性质的重要方法，也是探究证明思路、寻找证明方法的重要途径；(12)证明要做到：出发点正确、推理过程正确，证明的依据是学过的定义、基本事实、定理、推论等.

上述具体观念不仅可以指引平行四边形的研究，还可迁移至矩形、菱形、正方形及陌生图形的研究中.

2.2 调研学生的初期理解

学生带着有关世界如何运作的前概念来到课堂，如果他们的初期理解没被卷入其中，那么他们也许不能掌握所教的新概念和信息，否则他们会为了考试的目的而学习它们，但仍会回到课堂之外的前概念[18].那关于平行四边形，学生的初期理解是什么？为此，在四边形单元学习之前对35名学生进行了调研(1)调研结果由北京市大兴德茂学校李宁老师提供..下面呈现部分调研题目及结果.

对于问题“请你给平行四边形下个定义”，学生的答题情况如表1所示.

表1 平行四边形定义答题情况统计表

除了一名学生没有答题之外，其余34名学生都回答了此题，其中一名学生给平行四边形下了4个定义.

由上述调研结果可以发现，学生对什么是定义有不同的理解.此外，根据范希尔理论，学生下定义的水平主要处于水平1分析及水平2非形式演绎.其中分析水平的学生为了给某类图形下定义，倾向于列出该类图形尽可能多的性质，如表1中的定义5，6，7；而非形式演绎水平的学生能识别定义一个图形需要的最小一组性质，如表1中的定义1，2，3，4；演绎水平的学生则能认识到一个形式化定义的特征及其等价定义.

对于问题：“请你研究平行四边形的性质，平行四边形有哪些性质？”学生的答题情况如表2所示.

表2 平行四边形性质答题情况统计表

由表2可知，学生对“什么是图形的性质”理解不同.此外，大部分学生不清楚定义和性质间的关系，他们将定义作为平行四边形的一个性质.(如，在将“平行四边形的对边平行”作为平行四边形性质的27人中，有26人将其作为了平行四边形的定义)而在数学上，概念的定义和概念的性质是直接被区分的，概念的性质都是在定义基础上推导出来的[19].

从调研结果可以发现，学生对“什么是定义、如何下定义、什么是性质、如何研究图形的性质”等问题的理解上有较大差异.其中有些理解是不充分的、有些理解是错误的.而不充分、不恰当、错误的已有知识可能误导或阻碍新的学习[20]，因此需要通过教学予以填补和纠正.

2.3 制定学习目标、确定基本问题

理解为先的单元包含四种不同的学习目标：迁移、理解意义、知识和技能[21].学会迁移是所有教育的长期目标，学习的根本目的是理解意义与迁移应用；理解意义是迁移的前提，指向大观念；知识和技能是获得深入持久理解以及学会迁移的必需工具(即手段)[22].

为了促进学生的理解和迁移，需要有基本问题的引领.基本问题指向和突出大观念，它们像一条过道，通向理解之门；基本问题能够引发探究、讨论或论证；不仅能够促进对某一特定主题单元的内容理解，也能激发知识间的联系和迁移[23].

四边形单元的学习目标及基本问题如表3所示.

表3 四边形单元的学习目标及基本问题

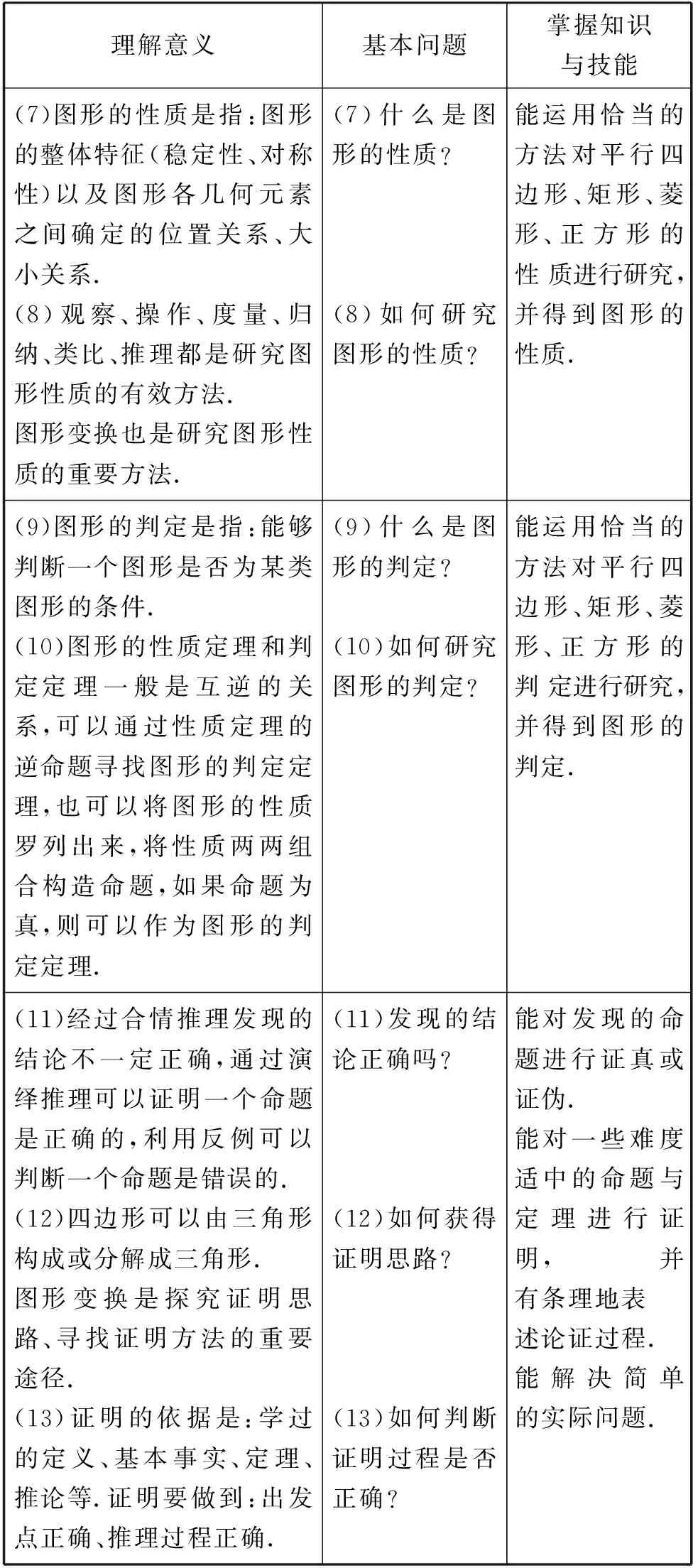
续表

2.4 设计评估任务

威金斯提倡逆向设计，即将评价设计这一步骤提前，先思考如何开展评估，再设计学习任务.评估的方式是多样的，包括对理解的非正式检查(如口头提问、观察、对话)、随堂测验、开放式问答题及表现性任务[24].为了评估学生的理解和迁移，可设计如下评价任务：图1中的三个四边形都是筝形，图2中的三个四边形都不是筝形.请给筝形下定义，研究其性质和判定，并给出研究结果.

图1

图2

2.5 设计学习任务

根据前述分析，将四边形单元的主要学习活动整体安排如下，如图3所示.

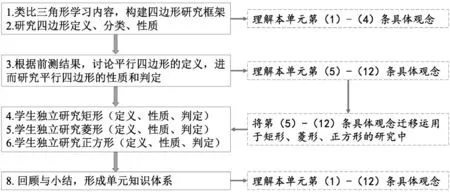
图3 四边形单元学习任务整体设计

限于篇幅，下面重点对平行四边形的学习任务予以展开，以问题串的形式呈现.

问题1课前请同学们给平行四边形下定义，同学们给出了7个定义，那这7个都能作为平行四边形的定义吗？

生：第一个肯定能，小学课本里是这么写的.

追问1：那其余6个呢？能作为平行四边形的定义吗？

生：之前学过定义具有两重性，定义既是“性质”又是“判定”.那需要判断其余6个是否具有两重性.也就是说先看看它们是不是平行四边形的性质，再看看它们是不是平行四边形的判定.

设计意图前测中，学生给平行四边形下了7个不同的定义，说明学生对定义有着不同的理解.那什么样的理解才是正确的呢？课堂上应该对该问题进行讨论，否则会不利于学生形成对定义的正确理解.学生会认为定义是教材给定的、是唯一的.

问题2既然如此，那我们在定义1的前提下，先来讨论平行四边形的性质.课前大家已经对平行四边形的性质进行了研究，得到了不少结论(呈现学生的研究结果).大家是怎么得到这些结论的？这些结论正确吗？怎么证明？这些都是平行四边形的性质吗？平行四边形的性质指的是什么？教材中为什么只呈现了其中3条性质？

设计意图定义具有两重性，既是“性质”又是“判定”.给概念下定义首先要清楚图形的性质和判定.因此，需要先对平行四边形的性质进行研究.通过问题2中基本问题的讨论，让学生理解本单元第(6)(7)(10)(11)(12)条具体观念.

问题3研究完性质，接下来我们研究平行四边形的判定.平行四边形的判定具体要研究的问题是什么？

生：寻找除定义外，能够判断一个四边形是平行四边形的条件.

师生活动：学生先独立研究，然后小组交流，老师观察并收集汇总学生的做法.

追问1：大家是怎么得到这些结论的？这些结论正确吗？怎么证明？

追问2：这些都是平行四边形的判定吗？平行四边形的判定指的是什么？教材中为什么只呈现了其中3条判定？

设计意图通过问题3中基本问题的讨论，让学生理解本单元第(8)(9)(10)(11)(12)条具体观念.

问题4研究完平行四边形的性质和判定，我们再回过头来讨论平行四边形的定义.除结论1外，其余6条结论可以作为平行四边形的定义吗？

生：结论2，3，4可以.结论5，6，7都有多余的条件，只需要保留其中一个即可.

追问1：平行四边形可以有多个定义吗?

追问2：教材为什么选择了“两组对边分别平行的四边形是平行四边形”作为定义？

追问3：根据前面的讨论，大家能说说如何给平行四边形下定义吗？

设计意图通过问题4的讨论，让学生明晰平行四边形可以有多个定义，而且这些定义是等价的.一般来说，人们选择更加直观的命题作为定义[25].定义是推理的逻辑起点，是研究性质和判定的出发点.给平行四边形下定义时，首先对平行四边形的性质进行探索，找出能够将平行四边形跟其他图形区分开来的性质，选择一条作为定义，然后对其进行检验，如果不能找到任何一个反例，则所下定义是恰当的.即通过对问题4的讨论，让学生理解本单元第(5)条具体观念.

问题5我们已经对平行四边形进行了完整的研究，下面我们进行回顾与小结.对于平行四边形我们都研究了哪些内容？是怎么进行研究的？得到了哪些结论？定义、性质、判定之间的关系是什么？

设计意图通过问题5，对平行四边形的研究过程进行回顾和整理，进一步明晰和理解本单元的具体观念，以便于迁移至本单元矩形、菱形、正方形及陌生图形的研究中.

3 结语

教育工作者希望学生能把学习从一门课中的一个问题迁移到另一个问题，从一学年迁移至另一学年，在学校与家庭之间以及从学校迁移到现场[26].而对基础性原则和观点的理解是培养迁移能力的主要途径[27].因此，为了促进学生的理解和迁移，可以在大观念的统领下进行单元教学设计.本文以四边形单元为例，阐述了如何在大观念的统领下进行单元教学设计：确定大观念及单元具体观念、调研学生的初期理解、制定学习目标并确定基本问题、设计评估任务、设计学习任务.大观念统领下的四边形单元教学设计体现了单元的思想，有利于学生深入理解定义、性质、判定间的内在联系，掌握研究一个图形的基本路径和思想方法，积累研究图形的活动经验，从而促进学生将所学内容迁移至陌生图形的研究中.