基于小波包能量熵和DBN的MMC-HVDC输电线路单极接地故障定位方法

叶鑫杰，兰生，肖思捷，原永滨

(福州大学电气工程与自动化学院，福州350108)

0 引言

基于模块化多电平变换器的高压直流输电(modular multi-level converter-high voltage dirrect current, MMC-HVDC)技术具有控制灵活、谐波含量低、开关损耗小等诸多优势[1 - 3]，因此在高压直流输电领域具有开阔的应用前景。采用架空线路的MMC-HVDC输电系统在进行长距离输电过程中，受沿线气候与地理环境变化的影响较大，导致线路故障率高，其中发生单极接地故障占比较大[4 - 6]。由于输电线路缺乏故障的自清除能力[7]，使得高发的瞬时性直流输电线路故障在一定程度上危害了系统的稳定性。因此，当直流输电线路发生故障时，确保精准可靠的故障定位是系统稳定运行的重要前提。

行波法[8 - 12]是直流线路故障定位的主要方法，理论上其不受输电线路参数影响，但对设备采样频率要求高，且存在行波波头识别困难，抗干扰能力差以及双端同步误差等问题，易对最终的定位精度造成影响[8]。文献[10]基于双端行波法，将双端行波波头到达时刻的瞬时频率与波速有机结合，取得了较好的故障定位结果，但需要依赖全球定位系统(global positioning system, GPS)对双端数据进行同步处理，存在同步误差问题。文献[11]提出一种通过提取行波固有频率的方法来确定故障的位置，该方法无需识别行波波头到达时间，但不同的过渡电阻会导致每个频率分量的微小变化，从而可能导致定位误差。文献[12]提出将行波法与Bergeron理论相结合，在无需进行双端时间同步的情况下，运用双端行波实现故障定位，但总体而言，时域行波测距方法还是存在无法准确标定初始波头的问题，尤其是由色散效应导致不同频率的行波波速不一，使得波速的选择问题未能很好解决。同时随着故障接地电阻的增加，故障行波特征也随之变弱，难以检测到线路浪涌，使得定位误差进一步加大。虽然一些方法对行波法进行了改善，但依然难以精确捕捉到高阻接地故障的故障特征，从而产生定位误差。

近年，智能算法的发展为高压直流输电故障诊断方面领域提供了新的思路。例如，Johnson等利用支持向量机(support vector machine, SVM)实现对高压直流线路的全套故障诊断方案，但并没有考虑过渡电阻因素对故障定位的影响[13]。文献[14]提出使用人工神经网络进行柔性直流输电故障检测。Lan等运用卷积神经网络在高采样频率下实现了输电线路故障定位，但在低采样频率下无法验证其定位性能[15]。

小波分析的非平稳信号分析能力在故障暂态信号的特征提取上发挥了一定作用[16 - 17]。Livani等将SVM和离散小波(DWT)相结合，实现了缆线混合线路故障判别和定位[18]。小波分析可以根据故障信号自身特性逐步分解为不同频率的子分量，但由于分解得到的信息庞杂，使得随着建立的神经网络系统也过于庞大[19]。因此，亟需对小波分解得到的大量信息进行深层数据挖掘，从而对数据规模进行缩减，避免维数灾难。本文采用提取故障信号的小波包能量熵以解决该问题。

深度信念网络 (deep belief network, DBN) 由 Hinton[20]于2006年提出，凭借其独特的结构和训练方式，在提取特征和处理非线性数据上展现了显著优势，并且已经在诸多领域都取得了成功[21 - 22]，故本文考虑将DBN首次引入柔性直流输电故障定位领域。当前，针对单极接地故障定位的研究大多采用小于500 Ω的过渡电阻，实际架空线路接地故障的接地电阻有可能高达数千欧姆[15]。因此，本文着重研究高接地电阻情况下的单极接地故障定位，提出了一种基于小波包能量熵(wavelet packet energy entropy, WPEE)和深度信念网络的故障定位方法，简称WPEE-DBN。该方法无需进行双端时间同步和标定初始行波波头的到达时间，避免了采用传统双端行波法需要依赖于通信技术、存在双端同步误差以及无法准确检测初始波头等问题。通过串联双端故障电压波形作为原始故障波形，运用小波包分解提取小波包能量熵作为故障特征量，并以此搭建DBN故障定位模型实现故障定位。为了避免DBN在训练时陷入局部最优，提出利用PSO寻优DBN的模型参数，旨在获得最佳故障定位效果。通过电磁暂态仿真软件PSCAD/EMTDC搭建±250 kV的MMC-HVDC系统模型，用于模拟故障并获取故障波形。实验结果表明，该方法可以在20 kHz的低采样频率下，精确可靠地定位过渡电阻高达4 000 Ω的单极接地故障。

1 MMC-HVDC单极接地故障分析

MMC-HVDC系统通常由交流系统、整流侧、逆变侧换流站和直流输电线路等重要部分组成，其系统结构图如图1所示。该系统的双端换流站均采用模块化多电平换流器(modular multilevel converter，MMC)拓扑结构进行功率传输。为了使双极系统直流线路对地呈现出对称的正、负极性，必须在直流侧或者交流侧设置接地点，本文采用直流侧钳位电阻接地的接地方式。根据图1所示的MMC-HVDC拓扑结构，利用PSCAD/EMTDC搭建完整的系统模型，对不同条件下(不同故障位置、不同接地电阻)的单极接地故障进行仿真模拟，并以20 kHz的采样频率对故障波形进行采集。

图1 双端MMC-HVDC系统结构图Fig.1 Structure of a double-ended MMC-HVDC system

由于采用的接地方式为小电流接地，在直流线路发生单极接地故障时，故障电流没有对地回路，桥臂电压因此不会改变，进而由桥臂电压组成的直流侧母线电压也将保持不变，线路电流仍为额定值，故MMC-HVDC输电系统的功率传输也将会正常进行[23]。故障仅改变了两极的参考电位，故障极的线路电压降至0 V左右，而非故障极电压将会增大为额定值的2倍，交流侧电压会出现直流分量，交流侧线路的对地电压应力也会随之升高。

对于双极MMC-HVDC直流输电线路，正负极线路间必然存在耦合。当发生线路故障时，耦合现象尤为明显。因此，在处理故障行波之前需要进行极模变换，以消除线路的极间耦合现象[15]。利用式(1)对双极线路电气量进行解耦，同时得到地模分量和线模分量。

(1)

式中：Ap和An分别为正、负极电气量；Ap0和Ap1分别为地模和线模分量。

当输电线路发生非金属性单极接地故障时，故障所产生的故障行波地模分量幅值如式(2)所示。

(2)

式中：Zc0、Zc1分别为地模、线模直流输电线路波阻抗；Uf为系统正常运行时的直流电压；Rf为过渡电阻。由式(2)可知，过渡电阻值与故障电压、电流行波地模分量幅值成反比，即过渡电阻值越大，则故障行波幅值越小。图2展示了在相同故障点下过渡电阻值相差较大的整流侧故障极对地电压波形，通过对比可以看出，过渡电阻值相差较大的故障电压波形存在显著差异。

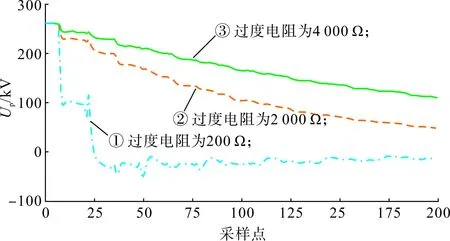
图2 不同过渡电阻故障电压波形Fig.2 Fault voltage waveform of different transition resistance

故障点处产生的行波可看作一个近似阶跃波，且该行波包含丰富的频率成分，其中高频分量波速快，低频分量波速慢[24]。因此，故障距离越远，行波在输电线路上传播距离也随之增加，不同频率的行波分量之间的距离变大，阶跃波将被拉长为畸变阶跃波，即产生色散效应，如图3所示。

图3 不同故障点的故障电压波形Fig.3 Fault voltage waveform at different fault points

综上所述，不同过渡电阻和不同故障位置是影响故障行波的两个重要因素，如何减小过渡电阻因素对故障电压波形的影响，从而更好地从波形中提取故障位置特征成为了实现精确故障定位的关键。虽然故障极电压降至0 V，但由于传输线路行波过程的作用，使得在故障时的电压波形中包含丰富的频率分量，具有明显的暂态过程，故可深入探索基于故障电压暂态特性的故障检测方法，以实现精确可靠地单极接地故障定位。

2 故障定位方法

由上一部分的分析可知，故障位置的特征蕴藏在故障行波的高频分量中，所以这部分将针对故障行波进行深层位置特征提取，并提出一种基于小波包能量熵和DBN的MMC-HVDC单极接地故障定位方法。首先，将双端录波设备采集得到的双端故障电压波形串联形成原始故障波形，该过程只需双端故障数据互通即可，并不要求双端时间信号同步。然后，通过对原始故障波形进行小波包分解并计算出各频带的小波包能量熵，以此构建新的特征向量矩阵作为深度信念网络的输入。最后，通过利用PSO算法对DBN的模型参数进行寻优，以实现精确可靠地故障定位。由于过渡电阻值相差较大的故障电压波形有较大的差异，若直接将阻值相差较大的特征向量送入DBN进行训练，其定位结果必然将受到过渡电阻因素的严重干扰。因此，在进行故障定位前先将特征向量按一定范围的过渡电阻进行分类，以减小过渡电阻因素对定位结果的影响。图4展示了所提方法的流程图。

图4 WPEE-DBN方法流程图Fig.4 Flow chart of WPEE-DBN method

当发生接地故障时，双端录波设备在各自检测到电压突变后开始以20 kHz的采样频率进行采样，采样窗口为250个采样点(由检测到故障时刻的前5个采样点与后244个采样点组成)，且由于行波在输电线路上传输时间不同，双端录波设备开始采集信号的起始时间也就不同。模拟的直流线路全长为200 km，假设行波波速为2.95×108m/s的情况下，250个采样点的采样窗口足以采集故障行波在输电线路上多个来回的信息。换句话说，这个采样窗口能够反应故障行波多次到达端点的信息，进而可以通过提取各突变点的相对位置特征来判断故障距离。在采集并串联双端故障波形后，通过小波包能量熵与DBN的结合实现故障定位，无需检测初始行波波头的到达时间。因此，所提方法可以很好地避免了采用传统行波法对采样频率要求高、存在双端同步误差、无法准确标定初始波头等问题。

2.1 小波包能量熵

小波变换是表示时频域内瞬态信号的有效工具，通常采用多分辨率分解将信号分解为不同频率尺度下的分量，但其只能对信号的低频部分进行进一步分解和处理，这样会导致一些重要的特征信息丢失。相比之下，小波包分解可以将每一层分解得到的高频、低频分量都进行再分解，这使得它可以在更全面的频率范围内获得更深层次的故障瞬态特征，为故障信号处理提供了更多的可能性。

能量是反映故障信息的关键特征，可以体现故障发生过程的变化程度。对故障信号进行小波包分解，第j层的第i个频带所对应的能量Ei,j如式(3)所示，即为该频带各小波包分解系数di,j(k)的平方和。

(3)

式中N为第i个频段的长度。则第j层的总能量可以通过式(4)来计算。

(4)

(5)

(6)

式中：Pi,j为小波分解j层时第i个频带的能量相对概率密度；EWPEE为小波分解j层时第i个频带的小波包能量熵。

在本节中，该部分是对故障波形进行预处理的过程，旨在从中提取深层故障特征。在发生单极接地故障后，整流侧和逆变侧以20 kHz的采样频率采集故障电压波形，并在信号突变时刻附近提取250个采样点。通过串联双端故障电压波形，形成长度为500的原始故障波形。将原始故障波形进行8层小波包分解可以得到256个不同频带的小波包分量，进而利用式(6)计算得到各频带的小波包能量熵，然后将各小波包能量熵按频带顺序排列，形成长度为256的一维特征向量，最后利用式(7)将小波包能量熵归一化到[0,1]之间，以此作为DBN模型的输入数据。

(7)

式中：xi为小波包能量熵向量的第i个数据；xmin和xmax分别为特征向量向量的最小值和最大值。以距离整流侧100 km处发生接地电阻为500 Ω的正极接地故障为例，新的特征向量提取过程如图5所示。

图5 故障特征波形Fig.5 Fault characteristic waveforms

2.2 深度信念网络

深度信念网络(DBN)是一个概率生成模型，由多个受限玻尔兹曼机(RBM)堆叠而成，这意味着RBM是DBN的基石[25]。RBM是一种无向模型，其包含一层可见层和一层隐藏层，各层的神经元层内无连接，层间全连接，其结构图如图6所示。

图6 RBM结构图Fig.6 RBM structure diagram

其中，vi为可见层的第i个神经元，可表示为v=[v1,v2, …,vn]，n为可见层神经元的数量；hj为隐藏层的第j个神经元，可表示为h=[h1,h2, …,hm]，m为隐藏层神经元的数量。基于以上的表述，RBM的能量函数为

(8)

式中θ为包含w，A和B的参数集。w={wij}∈Rn×m表示可见层和隐藏层之间的权重矩阵，其中wij为连接第i个可见层神经元和第j个隐藏层神经元的权重。A={ai}∈Rn和B={bi}∈Rm分别表示可见层偏差矢量和隐藏层偏差矢量。基于式(8)，当θ固定时，(v,h)的联合分布为：

(9)

深度信念网络模型的主要思想就在于运用逐层贪婪学习算法去训练深度神经网络的权重，从而实现从训练数据输入到预测输出的复杂映射和挖掘更深层次的数据特征。由3层RBM层和BP网络层构成的DBN模型如图7所示。

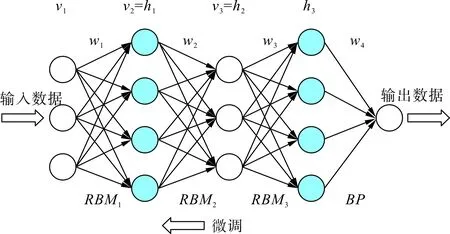
图7 DBN结构图Fig.7 DBN structure diagram

DBN模型训练过程分为预训练阶段和微调阶段。在预训练阶段时，输入信号从第一个RBM的可见层输入，并采用无监督的逐层贪婪学习算法训练各个权值与偏置。在训练完第1个RBM后，其输出数据将作为第2个RBM的输入数据，即前一层RBM的隐藏层将作为下一层的RBM的可见层投入训练，直到训练完所有的RBM。在微调阶段中，通过监督训练的BP网络进行反向误差传播，实现对模型的微调，以使模型收敛至最佳结果。通过对DBN的进行预训练和微调，可以实现对故障信号深层特征的进一步提取以及建立对输出的复杂映射。

本文共训练了5个DBN模型。第一个DBN为分类模型，它的作用是将特征向量按照一定范围的过渡电阻值进行分类，旨在减小过渡电阻因素对故障定位的干扰。通过模拟MMC-HVDC单极接地故障并采集0.1 Ω至4 000 Ω的过渡电阻所对应的双端故障电压波形，构造出小波包能量熵特征向量，然后将特征向量按过渡电阻的不同跨度分成0.1～1 000 Ω、1 100～2 000 Ω、2 100～3 000 Ω和3 100～4 000 Ω这4类，每类包含10个过渡电阻值，以此训练DBN分类模型，对应过渡电阻范围如图8中Cset1-4所示。其余4个DBN为回归模型，根据阻值范围将采集到的故障波形分为4类后，每类训练一个回归模型。考虑到工程实际中可能发生过渡电阻值不在各类别所覆盖范围内的接地故障，如1 000～-1 100 Ω之间的阻值所对应的故障。为了保证模型的泛化性能，故在进行故障定位时应考虑各接地电阻之间的重叠部分即将0.1～1 100 Ω、1 000～2 100 Ω, 2 000～3 100 Ω、3 000～4 000 Ω对应的特征波形作为各DBN回归模型的训练数据，对应接地电阻范围如图8中Rset1-4所示。以线路发生过渡电阻值为1 050 Ω的单极接地故障为例，提取故障行波特征后，将特征向量送入DBN分类模型，虽然该阻值处于各类别未覆盖的范围内，输出类别可能为Cset1或Cset2，但与这两个类别对应的DBN回归模型均已学习了包含该阻值的Rset1或Rset2中的特征信息，故依然可以实现故障精确定位。

图8 样本示意图Fig.8 Sample diagram

2.3 PSO算法

尽管DBN已经成功应用于许多领域，但不可否认的是DBN模型性能与其网络参数结构密不可分。DBN模型在训练过程中会由于模型参数选择不当而陷入局部最优，且很少有文献可以提供有效的策略方法来解决如何选择DBN网络参数的问题。因此，本文利用粒子群算法(particle swarm optimization algorithm，PSO)进行对DBN网络参数的优化，以取得最佳的故障定位效果。

粒子群优化算法的灵感来源于对鸟群捕食行为的研究，该算法具有简单且易于实现、算法内部需要调试的参数很少、收敛速度快等优势，其优化的目标是找到在约束条件下目标函数的最大值或最小值[26]。假设搜索的空间是n维空间，则种群中的第i个粒子可以用n维的向量Xi=[xi1,xi2,…,xin]T表示，粒子速度由另一个n维向量Vi=[vi1,vi2,…,vin]T表示，第i个粒子的最佳位置为pbesti=[pi1,pi2,…,pin]T,全局最佳粒子位置为gbesti=[gi1,gi2,…,gin]T。根据以下两个公式进行粒子群寻优计算：

(10)

(11)

式中：t=1, 2,…,n；i=1, 2,…,m，m为粒子的数量；c1、c2称为加速常数，且都为整正数；r1、r2为[0,1]范围内的随机数；ω为惯性常量，其值大小会影响整体寻优，为了避免陷入局部最优情况，通常该值在最大值ωmax和最小值ωmin之间线性递减，一般取ωmax=0.9，ωmin=0.4。本文选用的适应度函数为故障定位结果的平均绝对误差Eerr， 如式12所示。

(12)

式中：Wi为实际位置；prei为定位值；N为待测试定位样本个数。

3 系统仿真与实验结果

3.1 仿真模型与参数

利用电磁暂态仿真软件PSCAD/EMTDC根据图1拓扑结构搭建了双端201电平MMC-HVDC系统模型，其系统详细参数如表1所示。该系统为直流侧钳位电阻中性点接地拓扑，直流输电线路采用频变架空线路，其频变模型参数与杆塔模型参数如图9所示。整流侧采用定直流电压和定无功功率控制，逆变侧采用定有功功率和定无功功率控制。

图9 频变架空线路模型与杆塔模型参数Fig.9 Frequency-dependent overhead line model and tower model

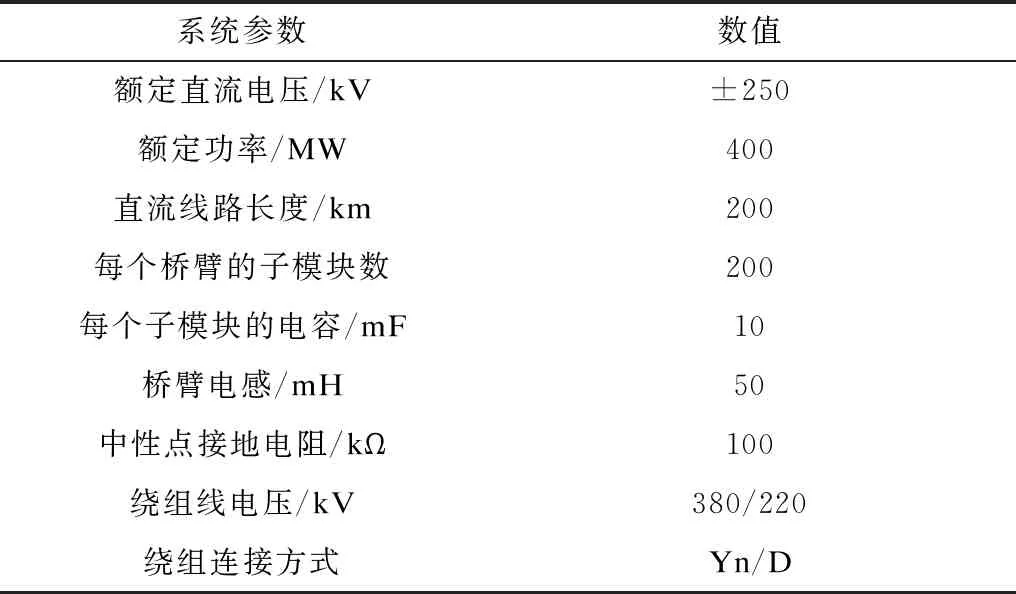
表1 MMC-HVDC系统模型参数Tab.1 MMC-HVDC system model parameters

基于搭建完毕的MMC-HVDC系统模型，在不同故障距离、过渡电阻等不同故障条件下进行单极接地故障模拟和采集双端故障电压波形，并从中提取小波包能量熵特征向量。本文考虑了低阻与高阻接地故障特征的不同，采集过渡电阻值为0.1 Ω至4 000 Ω的接地故障所对应的故障电压波形，以保证模型对不同过渡电阻的定位性能。需要说明的是，本文后续将0～200 Ω的故障视为低阻故障，阻值大于200 Ω则视为高阻故障。在模拟单极接地故障时，将故障发生时刻设置为1 s，采样频率为20 kHz，每间隔1 km设置一个故障点，根据设置不同的过渡电阻在每个故障点上采集40个故障数据，最终共采集8 000个故障电压波形以供后续工作处理。

3.2 故障定位模型参数的选取

人工选取DBN模型参数容易在训练时陷入局部最优，导致无法达到最佳的故障定位结果。而在DBN模型的各个参数中，RBM和BP网络的学习率和各层RBM的神经元数与DBN输出效果的好坏密切相关。RBM在训练时如果神经元数量过多，很容易发生过拟合现象；神经元数量过少则有可能无法充分学习样本特征导致陷入局部最优，从而影响最终的训练精度。而学习率是寻解过程中的步幅大小，决定着能否找到最优解和寻解的速度。因此，本文利用PSO算法寻优双层结构的DBN模型中的RBM、BP网络的学习率和各RBM层的神经元数。

在明确优化的目标后，对待优化参数设置寻优的区间：RBM第一层隐含层神经元数L1∈[10, 3 000]，第二层隐含层神经元数L2∈[10, 3 000]，RBM学习率∈[0.000 1,1]，BP网络层学习率∈[0.000 1,1]。PSO内部参数设置为：c1=2.6、c2=0.6、ωmax=0.9、ωmin=0.4、种群数量为50、迭代次数为100次，并采用式(12)作为适应度函数。PSO寻优结果如表2所示。

表2 PSO寻优结果Tab.2 PSO optimization results

尽管本文搭建了5个DBN模型，但各模型具有相同的模型参数结构。DBN分类与回归模型之间的区别在于，前者的输出层神经元数为4(分成4个阻值区间)，且该层的激活函数为“softmax”，旨在对每个类别的概率进行归一化；而后者输出层神经元数为1(一个位置值)，激活函数为“linear”，并利用均方误差作为损失函数计算定位误差。

为了测试所提方法的是否具有优越性，本文还搭建了基于支持向量机(SVM)的故障定位模型作为对照，该算法在解决小样本、非线性及高维模式识别中表现出独特的优势。SVM在近些年也被引入了高压直流输电领域，并利用其回归机制在低过渡电阻情况下的故障定位展现了不错的效果[10,14]。本文搭建的SVM模型采用高斯核作为核函数，并同样利用PSO算法寻优c和g这2个重要参数，PSO的内部参数与寻优DBN时保持一致，寻优区间设置为c∈[0.000 1, 100] ，g∈[50, 5 000]。最终选取c为1 100，g为0.01。

3.3 故障定位

根据第二节中所设置的样本分类标准，通过DBN分类模型将特征波形分为Cset1-4这4类，然后根据Rset1-4对应的各类特征波形分别训练DBN回归模型。训练单个回归模型过程中使用了2 200个特征波形，其中80%用于训练模型，剩余20%用于测试定位效果。使用SVM故障定位方法时，仅需将回归模型替换为SVM即可，其余步骤与上述均保持一致。同时，本文考虑将原始故障电压波形和小波能量熵特征波形分别作为模型训练数据，以测试小波能量熵对于故障特征的提取作用。通过式(12)计算可以得出各模型故障定位结果的平均绝对误差，如表3所示。为了直观地展示各模型定位结果，图10展示了各模型误差平均值的柱状图。

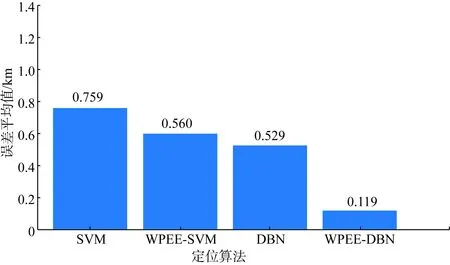
图10 各模型误差平均值Fig.10 Average errors of each model

通过表3和图10中各模型的故障定位结果可知，将使用原始故障电压波形作为训练样本的模型与使用小波包能量熵特征波形的模型相比较，后者的误差均呈现了显著下降趋势：WPEE-SVM较SVM误差平均值下降了25.83%；WPEE-DBN较DBN误差平均值下降了77.55%。显然，小波包能量熵可以有效地用原始故障波形中提取深层故障特征，将其作为特征量可以更好地表征故障发生的瞬态发展变化，进而大大提高故障的定位精度。与此同时，与WPEE-SVM方法相比，具备二次特征提取能力的WPEE-DBN方法定位误差大幅下降，在各阻值区间都展现更好的定位性能。

在测试了所提出本文所提方法的有效性以及具有良好的故障定位性能后，本文在高过渡电阻(200～4 000 Ω)的情况下，在每个故障点测试了10个阻值不同的故障数据，旨在更加针对高阻故障的定位效果进行测试。表4展示了各故障点的高阻故障测试结果。其中，距离表示模型的平均定位位置，平均误差表示10次试验中的平均绝对误差，最大误差表示10次试验中的最大绝对误差。

表4 高阻故障定位结果Tab.4 High-resistance fault location results

由表4可知，使用WPEE-SVM方法的平均误差为0.784 8 km，最大定位误差为3.225 km。相比之下，使用WPEE-DBN方法的平均误差仅为0.168 5 km，最大定位误差为0.953 km。在10个不同的测试故障位置中，WPEE-DBN方法的定位结果均比WPEE-SVM方法更准确，证明了所提方法在高阻故障情况下的优越性。图11显示了在高阻故障条件下各个故障位置的平均误差，可以更直观地看出所提方法对于定位高阻故障的出色性能。

SVM算法虽然在低阻故障情况下展现了良好的定位能力，但随着过渡电阻值的增加，故障特征也随之变得更加难以识别，这导致了依赖人工特征提取的SVM方法无法准确地定位高阻接地故障。而本文所提的出DBN方法可以利用自身网络结构的优势，自适应地提取故障高频分量特征，克服传统方法提取特征困难的问题，从而取得了更佳的故障定位效果。

图11 不同故障位置的高阻定位误差对比Fig.11 Comparison of high-resistance location errors under different fault locations

4 结论

针对MMC-HVDC输电线路高阻故障定位困难的问题，本文根据故障行波在传输线上的基本传输特性，提出了一种基于WPEE和DBN的单极接地故障定位方法。通过仿真实验，可以得出以下结论。

1)通过提取小波包能量熵可以实现对故障电压波形的深层特征提取。与直接使用原始故障波形作为特征量相比，将小波包能量熵作为新的特征量可以更好地表征故障发生的深层瞬态发展变化。通过实验证明，采用WPEE作为特征量的故障定位精确度相对于直接使用原始故障波形均有较大幅度的提升。

2)在高阻故障(200～4 000 Ω)情况下，本文所提方法的优势得到充分体现，其高阻故障定位平均误差仅为0.168 5 km。与同样使用WPEE作为特征量的SVM方法相比，所提方法通过利用DBN特殊的模型结构与训练方式对特征量进行故障特征的二次提取，避免了人工特征提取的局限性，从而使其定位性能在不同条件下的故障环境中均具有较大优势。