Kirchhoff动力学比拟对弹性薄壳的推广1)
薛纭 陈立群
∗(上海应用技术大学机械工程学院,上海 201418)
†(哈尔滨工业大学(深圳)理学院力学系,深圳 518055)
引言
弹性细杆的平衡与刚体的定点转动是两类完全不同的经典力学问题.1859 年Kirchhoff等[1-2]在平面截面假定下建立的弹性细杆静力学理论,依据其平衡的Kirchhoff方程与刚体动力学的Euler 方程在数学形式上的相似性,提出了Kirchhoff动力学比拟方法.1927 年,Love[3]在其弹性力学著作中详细叙述Kirchhoff理论,明确了两者在物理概念上的对应和在数学表达上的等同关系.对此,刘延柱[4]作了更明确的叙述,如中心线弧长坐标−时间;截面的姿态−定点转动刚体的姿态;截面的弯扭度−刚体的角速度;截面的抗弯抗扭刚度−刚体对主轴的转动惯量等.
促使弹性细杆力学近代发展的是分子生物学.作为脱氧核糖核酸(DNA) 双螺旋结构的力学模型,弹性细杆的Kirchhoff动力学比拟方法成为描述DNA双螺旋复杂位形的有力工具[5].Coleman 和Swigon[6]于2004 年由Kirchhoff方程得到有结和无结质粒超螺旋的精确解.从力学的角度看,动力学比拟也为连续弹性细杆提供新的离散化方法,从而成为3 自由度系统,弹性细杆的位形是截面沿中心线的弧坐标历程.位形、曲率和挠率等几何概念都可用弯扭度和Euler 角表达[4],开辟了用刚体动力学的理论和方法研究弹性细杆静力学的新思路,成为求解弹性细杆小应变大位移问题的有效方法.同时还极大地丰富了弹性细杆力学理论.分析力学方法[7]、非完整约束[8-9]、对称性和守恒量[10]、Lyapunov 稳定性[11],甚至混沌[12]等动力学概念和理论都可移植或应用到弹性细杆静力学,并赋予新的含义.同时Kirchhoff动力学比拟也为刚体动力学的运动历程提供几何直观图像.
弹性细杆中心线的二维扩展形成弹性薄壳的中面.自然希望将弹性细杆的Kirchhoff动力学比拟方法推广到弹性薄壳.
随着工程技术的发展,大型柔性航天器动力学和多柔体系统动力学应用日益广泛[13].文献[14]简要回顾了多柔体系统动力学建模的3 类方法:浮动坐标方法、几何精确方法和绝对节点坐标方法.对于大变形柔性梁,文献[15]在浮动坐标系下使用柔性梁参数方程形式的精确曲率公式来计算柔性梁的弯曲变形能,建立了基于浮动坐标系的考虑曲率纵向变形效应的刚耦合动力学模型.
对于几何非线性问题的建模与数值计算的主要方法有初应力法[16]、几何大变形约束法[17]、大变形耦合方法等[18].在大变形情况下,文献[19]提出了用绝对节点坐标法建模,解决了用混合坐标法建模计算效率较低的问题,文献[20]进一步用大变形实验验证了绝对节点坐标法的正确性.文献[21]不使用微分几何中的矩阵及其退化概念,在弹性中面的原始位形和当前位形之外,定义了平面参考位形,在这3 个位形上定义正交坐标系,通过映射表达他们间的关系.用Cartesian 坐标表达应变.
文献[22]指出,“显然,研究薄壳大变形大位移比研究刚体的一般空间运动更复杂,后者的自由度为6,而对可变形物体却有无穷多个自由度.”将Kirchhoff动力学比拟方法应用到弹性薄壳,有望将弹性薄壳化作离散力学系统,从而经典动力学理论和方法可以用到弹性薄壳力学,为弹性薄壳静力学注入新的概念和方法.
经典的弹性细杆和弹性薄壳的现代研究在对象,以及研究内容和研究方法上都赋予了全新的内涵[23].将弹性细杆Kirchhoff动力学比拟的思想,推广到弹性薄壳是很有意义的工作.在弹性中面上建立正交轴系并定义姿态坐标和弯扭度.用Lamé系数、弯扭度和姿态坐标表达中面偏微分方程、一点的应变和应力状态、截面的内力,以及平衡方程等.此外,弯扭度和Lamé系数还可表达曲面微分几何的基本概念和公式,这将另文讨论.
本文在直法线假设下[24-26],基于Kirchhoff动力学比拟方法和刚体动力学的观念,用Euler 角、弯扭度和Lamé系数讨论弹性薄壳的静力学建模.
文中指标取值i,j=1,2;k=1,2,3.
1 弹性薄壳中面的轴系
设O−ξηζ 为惯性参照系,沿坐标轴方向的单位基矢量为eξ,eη,eζ.变形前弹性中面上的任意点p变形后为P,中面方程分别为

其中q1,q2为广义弧坐标.设r和R具有所需要的各阶连续偏导数

为位移函数,如图1 所示.

图1 变形前和变形后中面上点的矢径和位移矢量Fig.1 The position vector and displacement vector of the point on the mid-surface before and after deformation
变形后中面上沿坐标线的切矢量、单位切矢量和弧长微分依次为
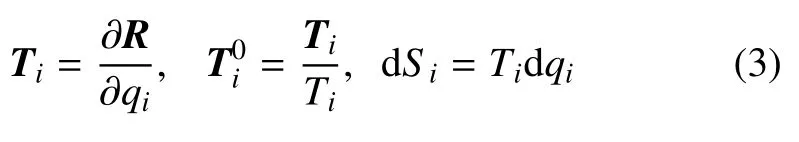
其中Lamé系数Ti=|Ti|.在中面上一点P建立两个轴系其中
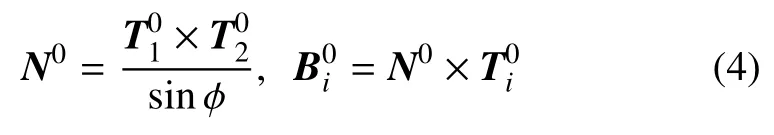
式中,N0为变形后中面的单位法矢量,sin φ=物理上要求如图2 所示.文献上称为点P的轴系,或Cosserat 方向子或活动标架.可以用线性表为
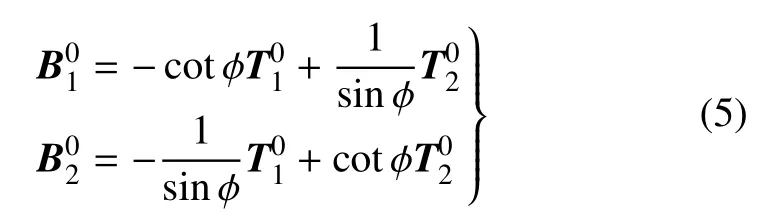

图2 弹性中面上两轴系的相对位置Fig.2 The position relation between two frames on the elastic mid-surface
对中面的任意曲线qi=qi(q)的单位切矢量

和其q坐标线的弧长微分dS,将式(5)第1 式代入式(6),化作
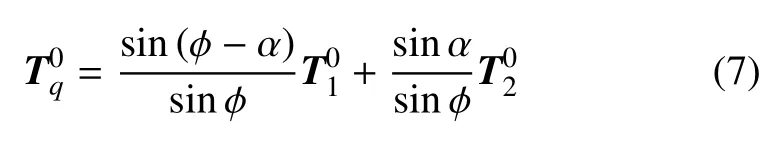
得到其弧长微分关系为
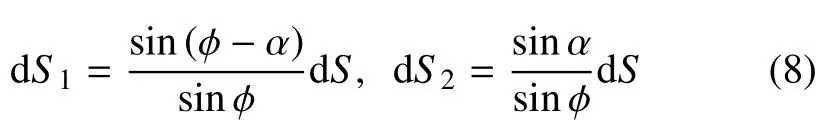

其中dS3是方向的弧长微分.

同理,上述概念可以在变形前的弹性中面上定义,并用下标0 表示

式中dsi为变形前中面坐标线的弧长微分.
2 弹性薄壳的弯扭度及其相容方程
2.1 弯扭度的定义

以变形前或变形后中面坐标线弧长微分为基准,即定义式中偏导分别对变形前和变形后的坐标线弧长进行,弯扭度分别记为三者的关系为

弯扭度的分量形式记为
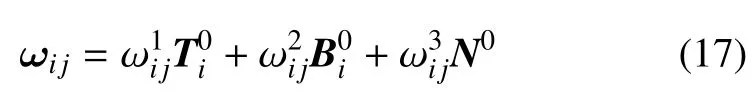
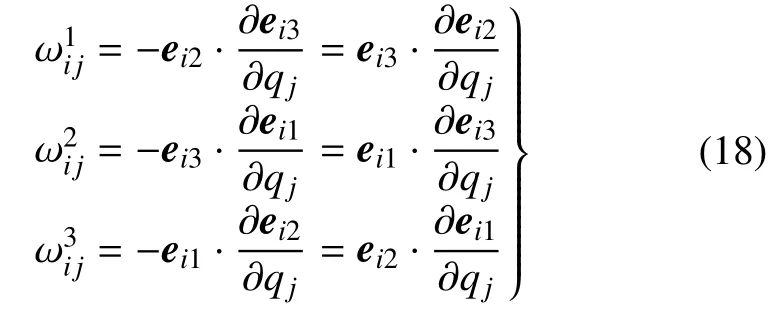
若矢量V写作V=VV0,其中V0为单位矢量.其偏导数用弯扭度表为
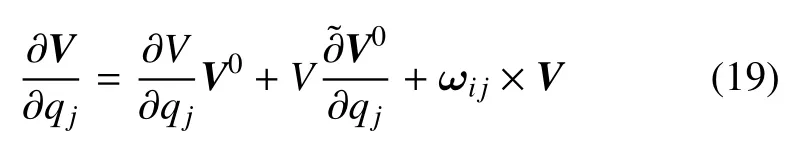
以变形前广义弧坐标微分dq为基准,沿任意方向的弯扭度定义为
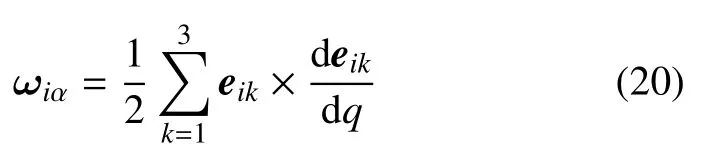
其中沿中面上曲线qi=qi(q)的单位切矢量为用沿坐标线的基于变形后弧长的弯扭度表为
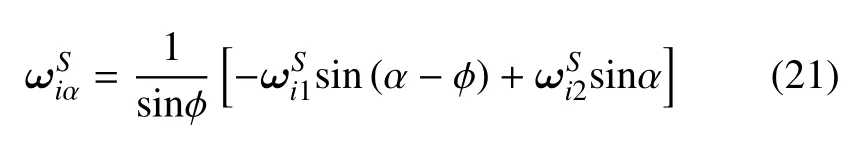
利用弯扭度的定义式(15),平面的弯扭度特征是

在曲面微分几何中,Rodrigues 方程指出了曲面主方向和主曲率的几何特征[28].当曲面的坐标线为曲率线时,有
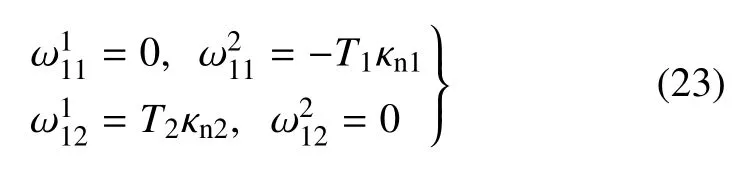
式中κni为两个主曲率.这也是Rodrigues 方程的弯扭度表达.它指出了主方向的弯扭度特征,进一步明确了弯扭度的几何意义.
2.2 等距面上的Lamé系数和坐标线夹角
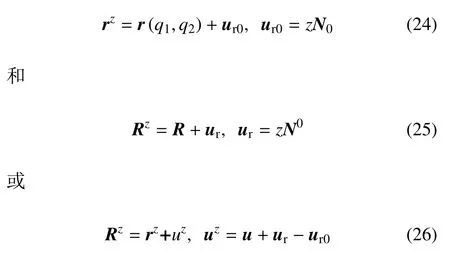
板壳中与中面等距离的面称为等距面.在直法线假设下,变形前和变形后等距面方程分别为其中h为弹性薄壳的厚度,z为厚度坐标(−h/2 ≤z≤h/2),N0为N0的原始值.
计算变形后等距面坐标线的夹角.等距面上沿坐标线的切矢量为
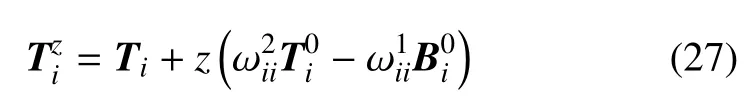
略去高阶微量,Lamé系数和弧长微分为

其中用到了对z的一阶近似.单位切向量为
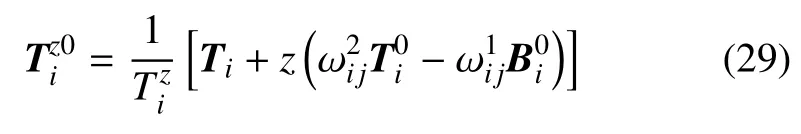
等距面上坐标线夹角φz由下式给出

在略去高阶微量后化作

同理,变形前沿坐标线的切矢量和单位切矢量有类似形式,这里不再赘述.
2.3 弯扭度的相容性
定义的弯扭度ωij不是互相独立的,存在相容协调关系.设弹性中面不可撕裂或折叠,这要求弯扭度是关于广义弧坐标的连续可微函数,并满足相容协调关系.
2.3.1 弯扭度ω1j,ω2j 的相容性
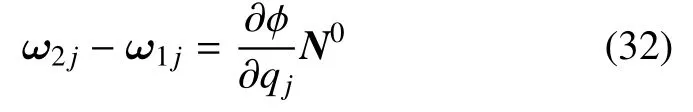
其在轴系(e21,e22,e23)上投影的矩阵式为
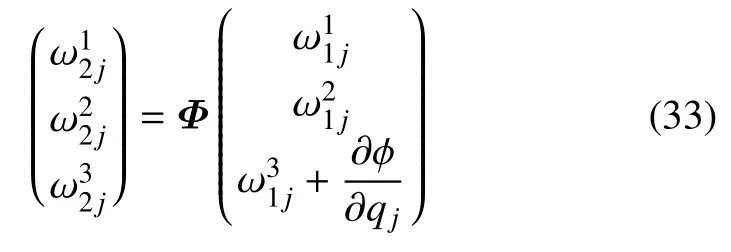
证明:对轴系(e11,e12,e13)和矩阵Φ,容易验证如下关系
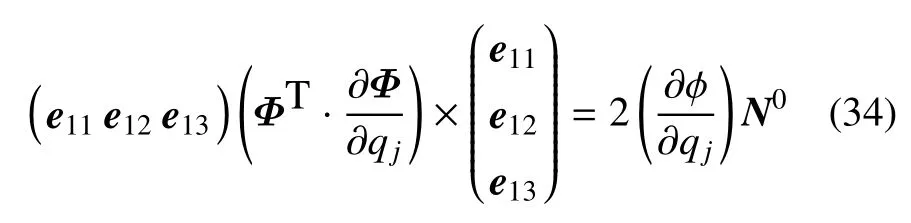
将式(10)代入式(15),即可导出式(32).再将ωij向轴系(ei1,ei2,ei3)投影,并注意到式(10),即得到式(33).
值得说明的是,式(32) 对任意方向的弯扭度也成立,即
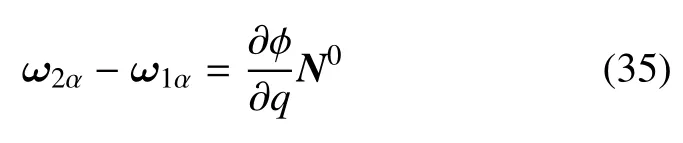
其中ωiα由式(20)定义.
2.3.2 弯扭度ωi1,ωi2 的相容性
弹性中面上同一个轴系沿不同坐标线方向弯扭度ωi1,ωi2的相容协调关系有下面四种等价形式
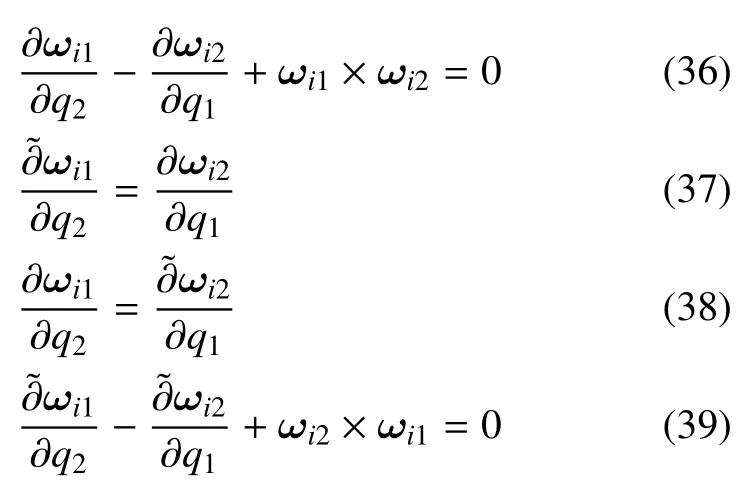
其中波浪号表示相对轴系(ei1,ei2,ei3)的偏导数.
证明:设a为给定轴系(ei1,ei2,ei3)中的固定常矢量,由式(19)依次对q1,q2求混合偏导数.由求偏导次序的可交换性,以及三重矢积恒等式,得到

因a为任意的固定矢量,于是就导出式(36).再由式(19),从式(36)导出式(37).同理可导出式(38)和式(39).
2.3.3 弯扭度相容方程的独立性
可以证明式(36)给出的两个式子可以互相推导,即
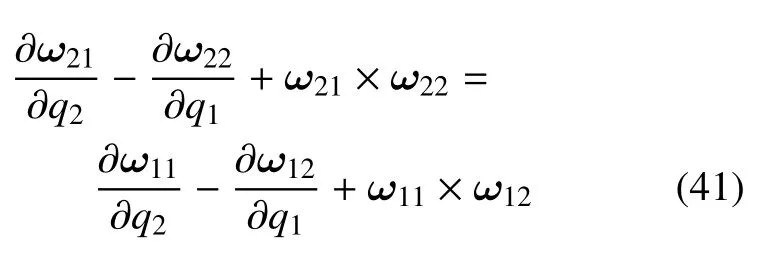
将式(32)代入式(41)等号左边即可推出等号右边.
2.3.4 中面上弯扭度与切矢量的相容性
弹性中面上弯扭度与一点的切矢量也必须是相容的.切矢量满足如下关系

这既是曲线积分

与路径无关的条件,保证变形后的弹性中面无裂缝;也是两沿坐标线切矢量的相容协调关系.
注意到Ti=式(42)写作

其分量形式为

这是关于弯扭度和Lamé系数的约束方程.由式(33),式(45)右端的弯扭度可用ω1i表达,化作
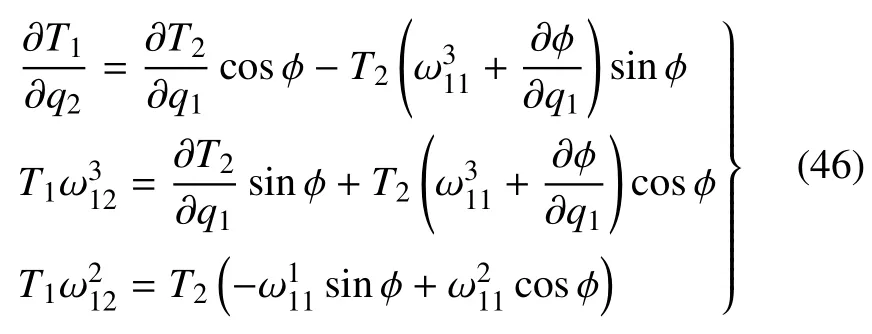
式(32) 和式(36) 及其等阶形式,以及约束方程(46),在弯扭度用Euler 角及其偏导数表示时再作进一步讨论.
3 轴系姿态和弯扭度中面偏微分方程
3.1 轴系姿态的Euler 角
建立惯性参照系O−ξηζ.借助Euler 角将轴系(ei1,ei2,ei3) 用惯性参照系的基矢量(eξ,eη,eζ)表达.为此将O−ξηζ 平移到弹性中面的P点,绕轴的如下三次转动到达轴系(ei1,ei2,ei3)的位置P−xyz,如图3 所示[4,29]


图3 轴系(ei1, ei2, ei3)姿态的Euler 角Fig.3 Euler angles of attitude of the frame(ei1, ei2, ei3)
基的变换关系用矩阵表为

其中Qi为方向余弦矩阵
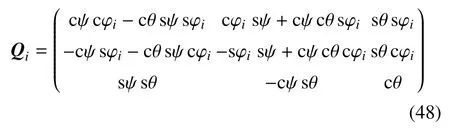
由图2 知,ψ2=ψ1,θ2=θ1,φ2=φ1+φ,可略去ψ,θ 的下标;ψ=ψ(q1,q2),θ=θ(q1,q2),φi=φi(q1,q2)为轴系(ei1,ei2,ei3) 相对于惯性系的Euler 角;字母s,c 分别表示sin,cos.
两方向余弦矩阵Qi之间有如下关系

式中Φ由式(10)定义.
当给定矩阵Qi,可以通过式(48)从对应元素相等解出相应的Euler 角[4,29].表达轴系(ei1,ei2,ei3)在惯性参照系O−ξηζ 中的姿态还可以用Cardano 角或Euler 参数等,这里不再赘述.
3.2 弯扭度的Euler 角表示
由刚体动力学知,用Euler 角表达的弯扭度ωij在基(ei1,ei2,ei3)下的矩阵式为[4,29]

将此弯扭度的Euler 角表达式代入弯扭度的相容方程(32) 和方程(36)~(39),都成为恒等式.表明弯扭度的相容方程对Euler 角不构成约束.弯扭度的Euler 角表达式将使式(45)和式(46)转化为对Euler角和Lamé系数及其偏导数的约束方程.
3.3 中面偏微分方程
在惯性参照系O−ξηζ 中,变形后弹性中面上一点P的直角坐标为
式(3)给出中面的偏微分方程的矢量形式


当已知Euler 角和Lamé系数ψ,θ,φ,φ;T1,T2随广义弧坐标qi的变化规律,且满足约束方程(46),式中弯扭度由式(50)给出,即
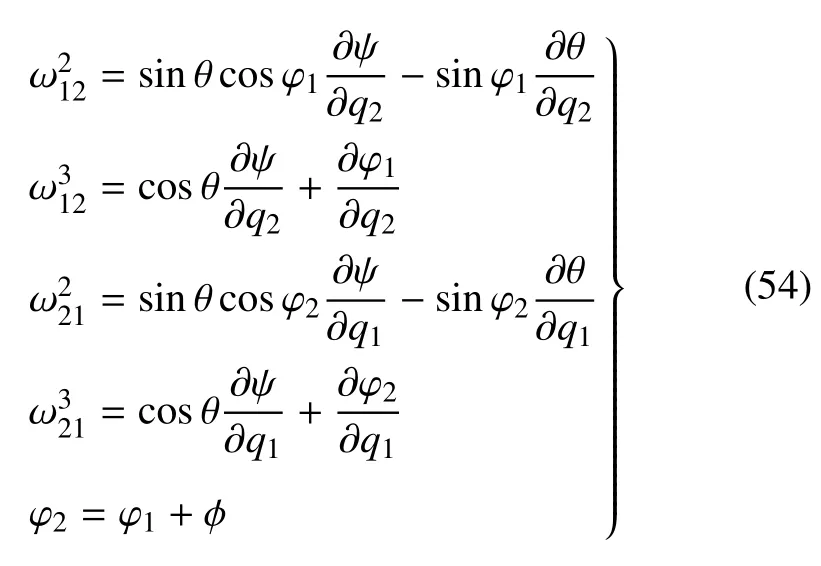
并且已知边界条件,如

就可以求得弹性中面的位形.
特殊地,当仅有i=1 时,式(53)即为弹性细杆的轴线微分方程,此时R为弹性细杆中心线的矢径,为其单位切矢量.可见这是弹性细杆轴线微分方程向弹性薄壳中面的推广.
4 应变和应力及其弯扭度表达
一点沿任意q坐标线方向的线应变定义为[30]

式中dS是微分弧段ds在变形后的长度,T=dS/dq,T0=ds/dq为相应的Lamé系数.可近似表为[30]
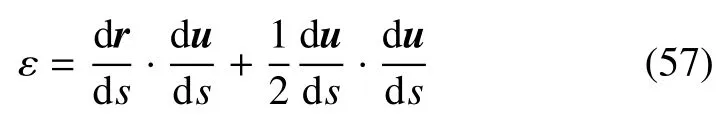
4.1 等距面上一点的线应变合成定理
等距面上一点的线应变合成定理:弹性薄壳变形后等距面上一点Pz沿坐标线qi的线应变等于中面上点P沿该坐标线的线应变εei和点Pz相对于点P的线应变εri,以及原始相对应变负值−εri0的代数和,表示为

其中ur由式(25) 定义,为其原始值由式(24)定义.
若变形前弹性中面为曲面,∂N0/∂qi≠0.将式(24)代入式(57),此时式中ε 为略去二阶以上小量便得到式(58).
下面用弯扭度表达εri,εri0.由式(25),得

代入式(61),取j=i,相对线应变εri用弯扭度表达为

即
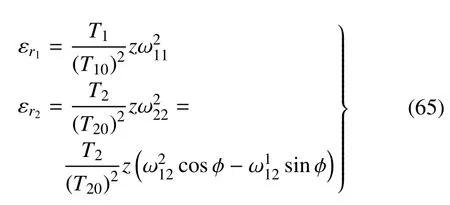
在应变的一次近似下,式中可取cos φ=0,sin φ=1,Ti/Ti0=1,写作

同理,可得

4.2 等距面上一点的剪应变
等距面上一点的剪应变合成定理:变形后弹性等距面上一点Pz的剪应变在一次近似下等于弹性中面上一点P的剪应变γexy和点Pz相对于点P的剪应变γrxy,以及变形前点pz的“剪应变”负值的代数和.表示为

推导如下:变形前弹性薄壳等距面坐标线一般不是正交的.因此,按照剪应变的定义,在小应变下有
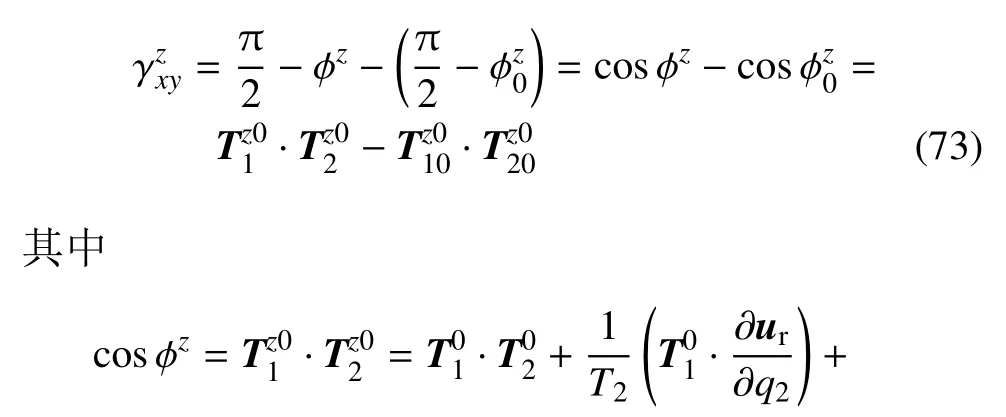

这就得到了式(68).
用弯扭度表达相对剪应变.由式(70)得

在应变的一次近似下,取T20/T2=T10/T1=1,式(77)和式(79)化作
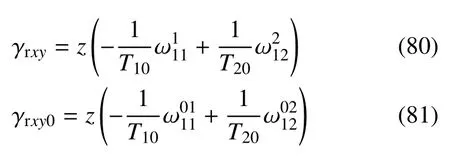
4.3 等距面上一点沿任意方向的线应变


这结果是显然的.
可以验证,薄板的经典大挠度理论是上述结果的特例.
4.4 应力及其弯扭度表达

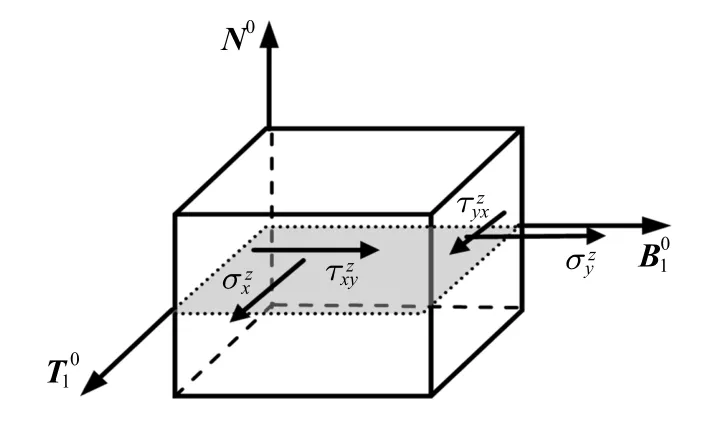
图4 直法线假设下计及的应变所对应的应力Fig.4 The stress corresponding to the strain considered under the straight normal assumption
设材料是线弹性的.由广义Hooke 定律知
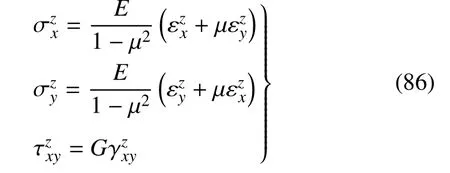
式中,E,G,µ分别为材料的拉压弹性模量、剪切弹性模量和Poisson 比,三者满足关系G=E/2(1+µ).
注意到式(84),将应变式(58) 和式(68) 代入式(86),式中应变分量由弯扭度和Lamé系数表达,得
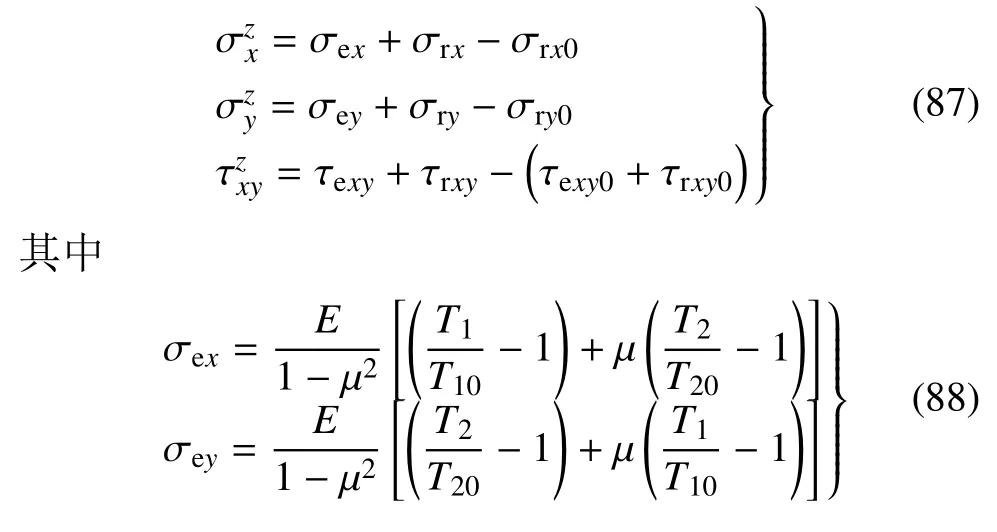

式中,σex,σey,τexy为薄膜应力,σrx,σry为弯曲应力,τrxy为扭转剪应力,而σex0,σey0,σrx0,σry0,τrxy0不具有应力的意义.
5 弹性薄壳截面上的分布内力和本构方程
5.1 弹性薄壳截面上内力的简化

微分单元截面上应力向中线简化的结果为一分布主矩和分布主矢,如图6 所示.
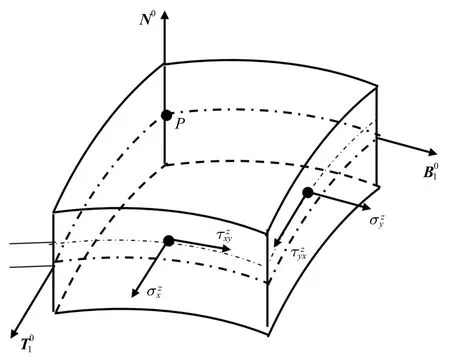
图5 微分单元及其计及应变的应力状态Fig.5 Differential unit and its stress state considering strain

图6 微分单元及其内力:分布主矩和分布主矢Fig.6 Differential unit and its internal force:Distributed principalmoment and distributed principal vector
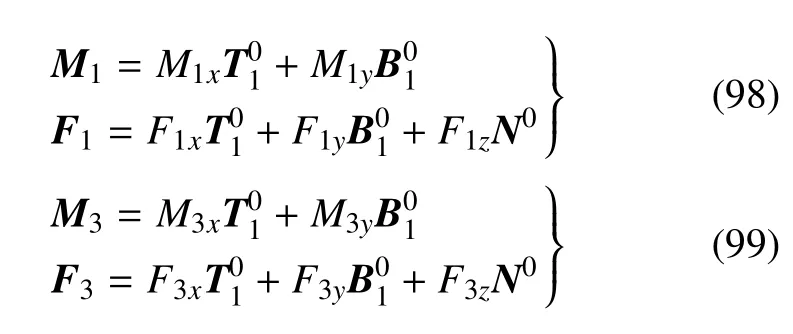
其中,M1x,M3y为分布扭矩,M1y,M3x为分布弯矩,F1x,F3y为法向分布力,F1y,F1z,F3x,F3z为切向分布力.具体表达如下
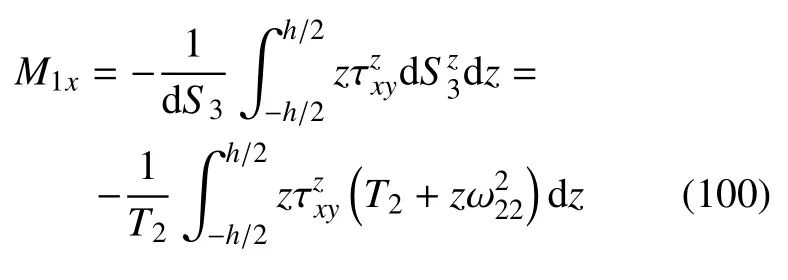
以下直接写为

可以验证,内力主矩和主矢表达式与经典的表达是一致的[24-26].
5.2 本构方程
由式(100)~式(105),得到本构方程
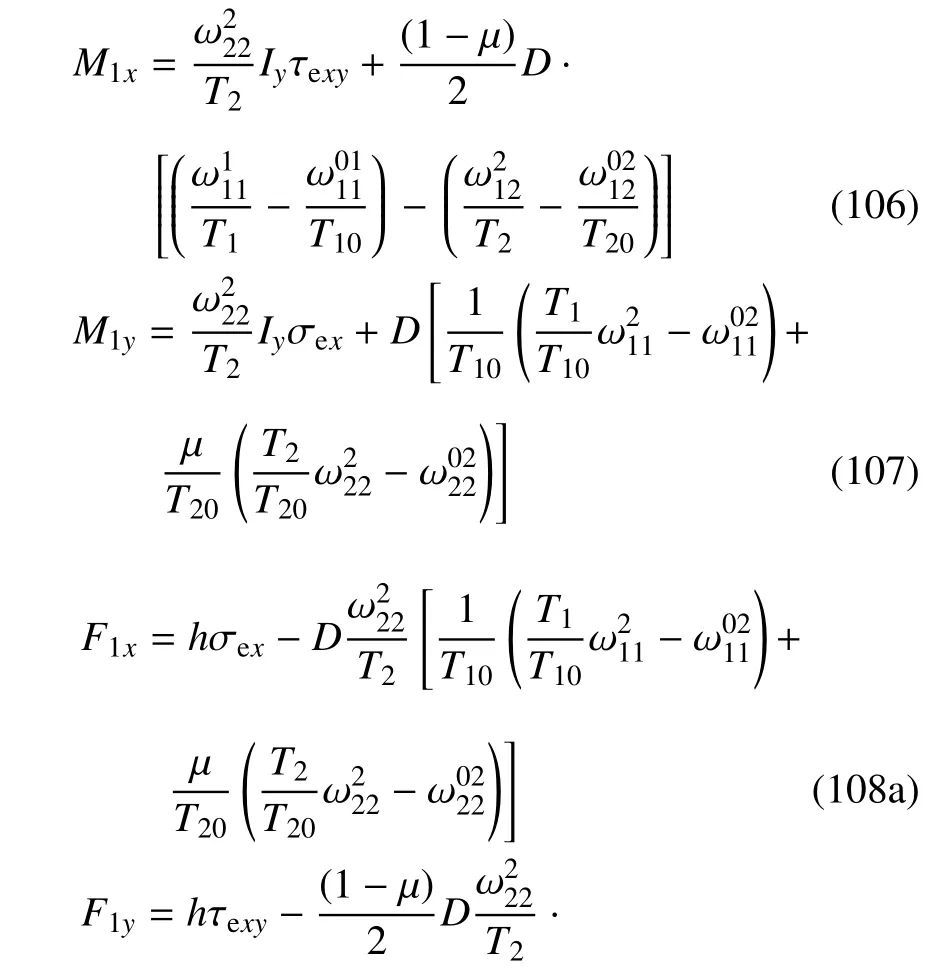
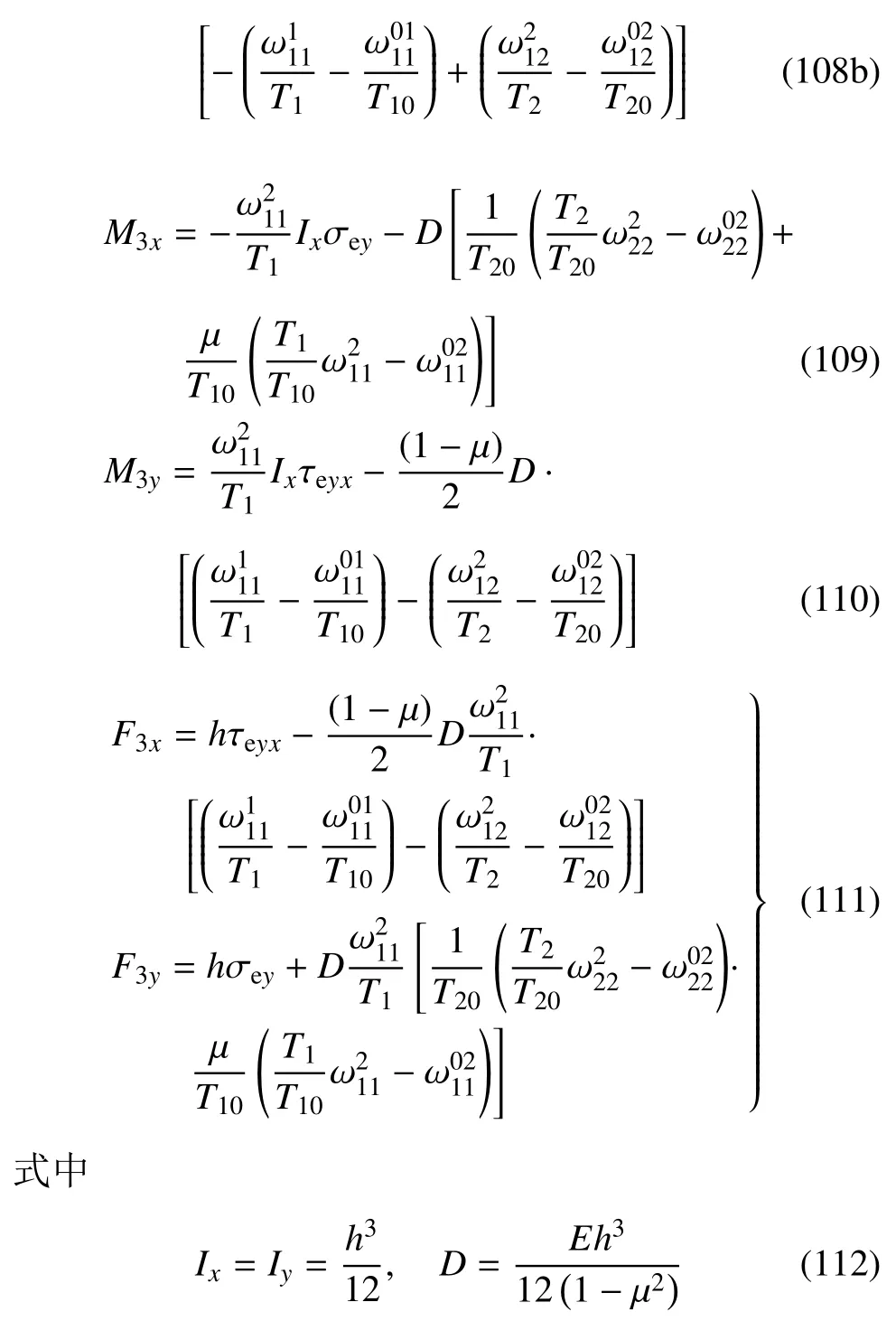
其中D为抗弯刚度.
根据直法线假定,F1z,F3z是独立变量.
本构方程也可以在应变的一次近似下表达,这里从略.
6 平衡方程和动力学比拟
6.1 平衡方程
设沿弹性薄壳中面作用有随体或固定的分布载荷

列出变形后微分单元的平衡方程并整理得

将式(3)、式(9)和式(97)代入,化作

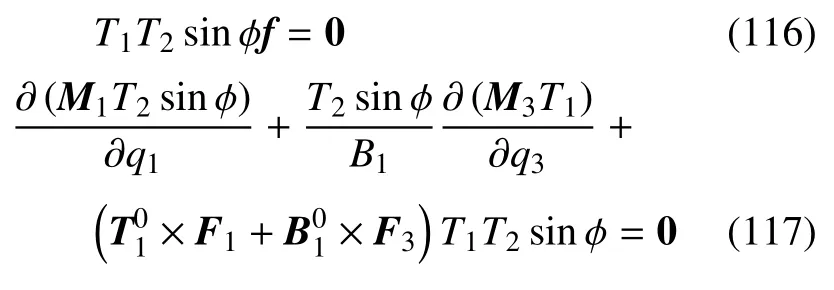
这形式上与Kirchhoff方程和Euler 方程相似,但多了一个自变量.与经典薄壳平衡微分方程也是一致的[24-26].
值得指出式(117) 的N0轴投影式不是独立的.不失一般性,当坐标线qi是曲率线时,φ=π/2,且有式(23)知,=0,可以证明式(117)沿N0的投影式是恒等式.需要注意的是,变形后的中面位形是待求的.
静力方程式(116)和式(117)是2 自变量的偏微分方程组,与约束方程(46) 联立,方程数位8,所含的未知量是ψ,θ,φ1,φ,F1z,F3z,T1,T2,个数相等.因此,方程组封闭.值得一提的是,这里的约束方程是运算和变形规则要求,因而无需对应的约束力,文献上称此类约束为内约束.
由复合函数的求导规则和式(9),有
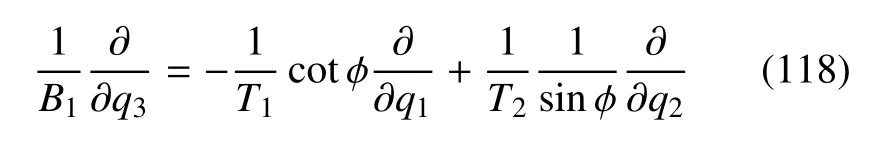
据此,可将对q3的偏导数化作对qi的偏导数.
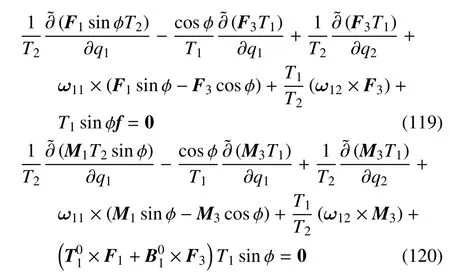
6.2 弹性薄壳的Kirchhoff动力学比拟
式(115)与定点转动刚体的Euler 方程和弹性细杆Kirchhoff方程有一定相似性.按照Kirchhoff动力学比拟,弹性薄壳静力学与刚体动力学有很好的对应关系,主要有:时间坐标t−中面广义弧坐标qi,Euler 角ψ,θ,φ–Euler 角ψ,θ,φi,角速度Ω−弯扭度ωij;刚体的运动过程−弹性薄壳的位形,动量矩−内力主矩等.弹性薄壳可以取刚体的姿态坐标和Lamé系数以及厚度方向的切向分布力为未知函数,按照求解刚体运动的思路求解弹性薄壳的位形.
7 算例
设薄板宽度为b,长度为l,厚度为h,不计自重.在板两端作用分布力偶

如图7 所示.变形前弹性中面的矢径为
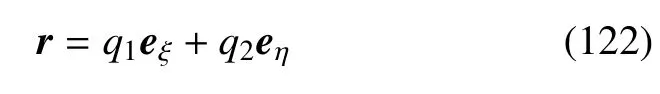
Lamé系数Ti0=1,轴系基矢量为
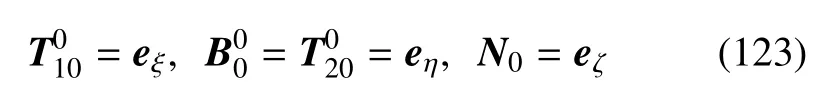

图7 变形前后的弹性薄板Fig.7 Thin elastic plate before and after deformation
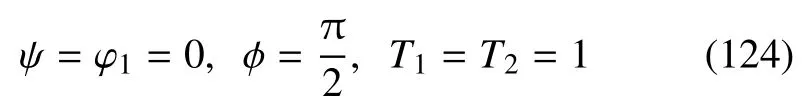

N0方向的投影式为恒等式.再将式(124)和式(125)代入式(119),解得

考虑到约束方程式(46),解为

积分得

此时的弯扭度和中面的应力为

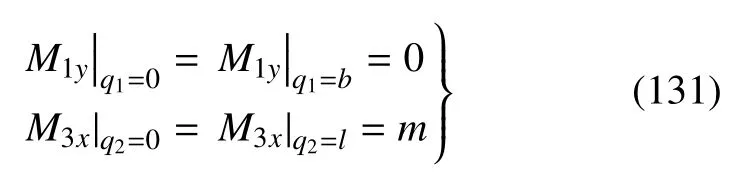
由式(107)得到

注意到φ=π/2 和式(129),式(109)化作

解得
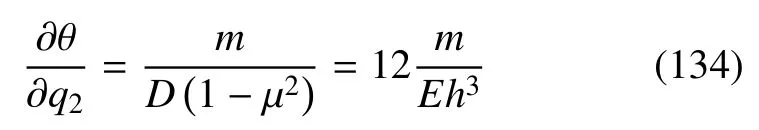
积分得
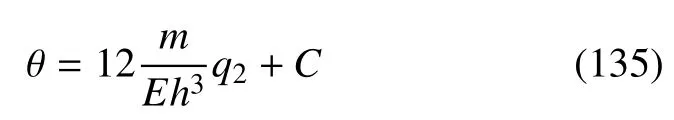
其中C为积分常数.设=0,导出C=−6ml/(Eh3).

由式(53)得到变形后的中面偏微分方程
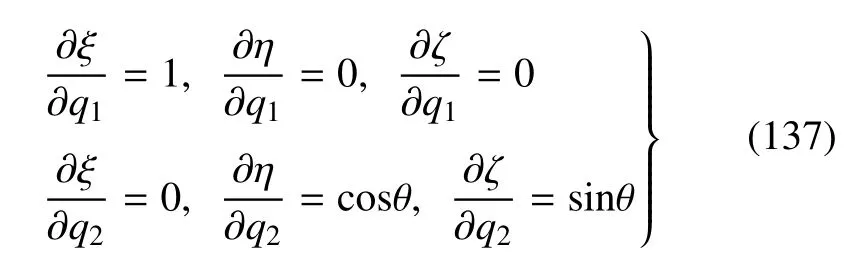

其中,K=12m/(Eh3).这就是薄板在两边分布力偶作用下的中面方程.是一圆弧面,圆心轴为平行于ξ轴的直线段(q1,l/2,1/K),半径为1/K.这结论是熟知的,如图8 所示.

图8 弹性中面的位形Fig.8 Configuration of elastic mid-splane
8 结论
用中面轴系的姿态坐标和弯扭度,以及Lamé系数表达了弹性薄壳中面的位形、一点的应变状态和应力状态、以及截面上的分布主矩和分布主矢,得到的平衡偏微分方程与定点转动刚体的Euler 方程和弹性细杆Kirchhoff方程有一定的相似性.使中面位形成为广义弧坐标历程.将弹性杆的Kirchhoff动力学比拟方法推广到弹性薄壳.
在Kirchhoff动力学比拟下,弹性薄壳的位形空间是是一个6 维空间,因为双自变量,且存在3 个非完整约束,因此自由度为9.可以引入完整和非完整约束的概念,并形成弹性薄壳的分析力学方法.

