高速列车服役模拟建模与计算方法研究1)

张卫华

(西南交通大学牵引动力国家重点实验室,成都 610031)

引言

高速列车的出现,为广大旅客提供了高效、便捷、舒适、高速的交通工具,改变了旅客出行的时空观.从1964 年高速铁路诞生半个多世纪以来,高速列车的安全运行始终是高速列车研究者和运维者最关注的问题.在进行高速列车关于乘坐舒适度与安全性的动力学研究中,如何反映高速列车运行的实际环境,开展更加精确的服役模拟成为研究热点.作者提出高速列车耦合大系统动力学[1-3],就是要以高速列车为核心,考虑线路、气流、弓网、供电等耦合子系统共同作用下的高速列车服役行为与动力学性能,实现高速列车服役状态的精确表征.与此同时,基于列车运行状态的健康管理与状态修,以实现高速列车能力与状态的保持,也是研究的热点.就列车中车辆而言,其服役状态除了受到列车编组及位置、车辆自身状态影响;还受到线路状态,包括线路不平顺、线路刚度等影响;甚至还受到列车的运行状态,如牵引、制动和惰行等运行状态的影响[3-6];最后还将受到运行环境,如风、雨、雪、气温等自然环境影响[7-13];这些影响相对独立,但在联合作用下,车辆的服役状态是综合影响的结果.因此,在进行高速列车(车辆) 健康状态评估的时候,不仅需要考虑车辆自身状态,同时需要考虑线路、运行、环境等其他因素的影响,以实现多维度下的状态评估,如图1 所示;另一方面,在定量确定车辆健康状态的时候,需要知道那些因素在如何影响着车辆的性能,才有可能得到车辆自身的健康状况,实现车辆健康度的评价.当然,在进行车辆状态修的过程中,还需要进一步考虑维修的经济性,实现车辆状态/能力保持与维修经济性的平衡.

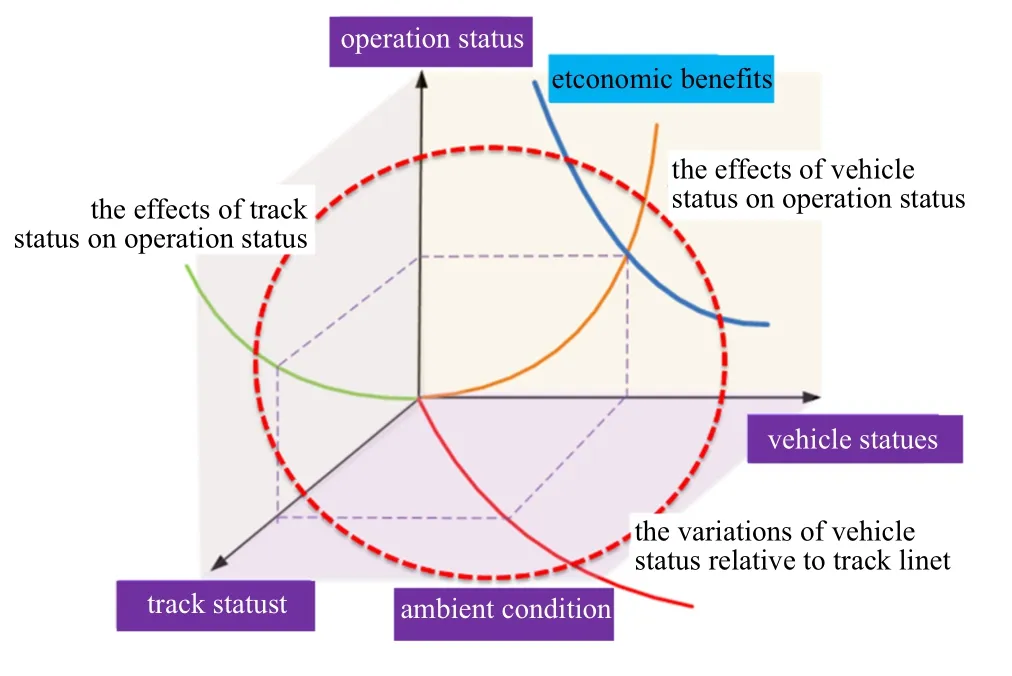
图1 列车运行状态及其影响因素Fig.1 Train operation state and its influencing factors

可以看到,考虑复杂运行环境的高速列车服役模拟成为高速列车运行安全评估和健康管理的重要内容,服役过程的模拟计算是重要手段.服役模拟的特点是真实还原高速列车运行的场景,包括列车编组、线路、环境、服役时间(周期)等因素.本文围绕高速列车的服役模拟,作者试图解开困扰服役模拟计算的几个瓶颈问题.

1 长编组列车建模与服役模拟计算技术

传统的车辆系统动力学,基本上以车辆为研究对象,而且仅仅考虑车辆匀速运动,也就是不考虑车辆的纵向运动(自由度).而实际上,在考虑纵向运动,甚至仅仅考虑列车中前后车辆的相互约束,车辆与列车的动力学响应(临界速度与振动加速度)就会有差别.作者在京津科学研究型试验[14]中就发现,一列8 辆车编组的列车,在运行中不同编组位置车辆的垂向、横向振动均是不一样的,这不仅与车辆位置,如头尾车还是中间位置相关;还与车辆的结构,是动车还是拖车,是否装有受电弓等相关,如图2 所示.因此,进行整列车的服役模拟是必要的.

图2 高速列车各车辆的振动加速度Fig.2 Vibration acceleration of high-speed train vehicles

由于高速列车的标准编组为8 辆,长编组可能达到16 或17 辆.如果要对列车建模,就必须对每节车进行建模,这就必须对每一辆车的每一个自由度都进行位置和运动方程的描述,建模工作繁重.在计算时,同时考虑所有车辆的所有自由度,方程的质量、刚度、阻尼矩阵庞大,造成计算困难.因此,商业车辆动力学计算软件,对计算自由度(也就是车辆数) 有一定限制.为此,需要发展新的列车建模与仿真计算方法,以支撑服役模拟.

列车编组型式基本上有动力分散与动力集中两种模式,如图3 所示.高速列车一般属于动力分散型模式,由若干动车和拖车组成.尽管高速列车中每一节车辆由于结构设计、定员数量和悬挂设备有所不同,导致参数有所差别,而且动车和拖车的转向架的结构上有一定差别,如动车有驱动系统,由此造成基础制动结构也与拖车有异.但在列车系统动力学研究时,往往列车中各车辆的运动自由度考虑成一致,也就是其动力学方程一致,这就给列车动力车建模与运行模拟创新带来机会.

假设列车中车辆模型是一致的,但参数可以不一致,这时车辆单位的模型为

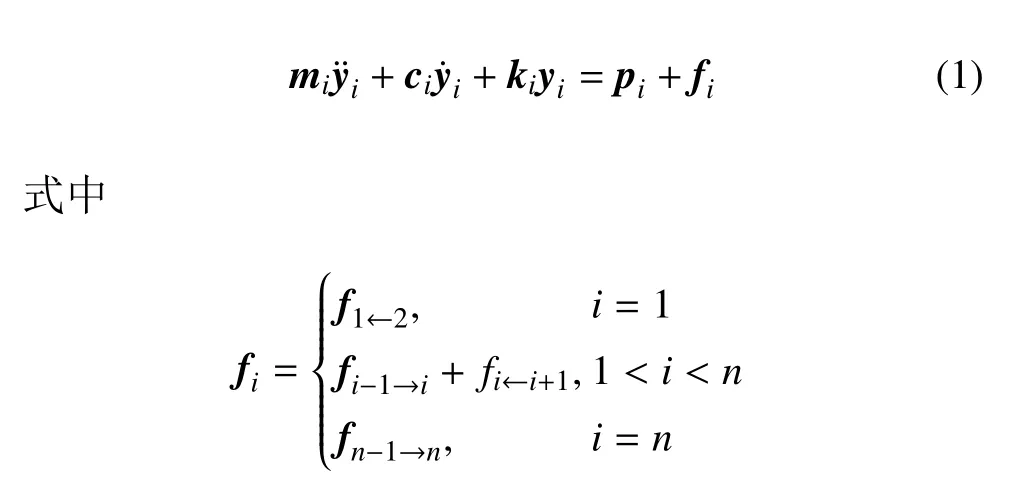
式中mi,ci和ki是第i节车的质量、阻尼和刚度矩阵,pi是作用在第i节车上的外部作用力,fi是车辆之间的相互作用力,其中是i节车前后相邻车之间的相互作用力,当然对于头车和尾车来说,只有一个车间相互作用力.

新方法不像传统的积分方法那样,需要在每一个时间步长一次计算出列车系统中所有变量的运动状态,而是把一节车看成一个基本的积分单元,先计算第一节车,再计算第二节车,这样一节车,一节车逐个进行计算,直到计算出最后一节车辆(尾车) 的运动状态,再进入下个积分步长.这样就把一个大系统的积分计算问题,变成n个小系统的积分计算问题,化繁为简.如列车由m节车辆组成,每节车有n个自由度,则整列车的状态矩阵是一个nm×nm的大矩阵,如果考虑降阶计算,矩阵更大.矩阵计算复杂而且费时,新方法每节车辆仅仅是一个n×n的小矩阵,计算方便快捷,无非是做了m次计算,相对于整列车矩阵中仅仅对对角线上的m个n×n矩阵进行了计算,从而大大节省了矩阵运算时间.在新的积分计算方法中,由于方程(1)和变量被重复使用,因此,新的积分方法可称之为循环变量法;由于在积分中从第一节车开始计算,后面车辆的计算用到前面已算出的新运动状态,达到递推的效果,因此也称递推积分方法[15].

积分计算时,根据车辆位置所对应的车辆模型,调用对应车辆类型的参数矩阵,并从临时矩阵中调用相应的变量状态和受力状态,进行积分.可以看到,采用新循环变量积分方法,不仅有效减少了求解规模,更大的优势是不需要写出所有车辆自由度的方程,而仅仅写出不同类型车辆的动力学模型,再定义列车编组不同类型车辆的编组位置,就完成建模,建模工作量大大减少.特别是,当列车编组发生改变时,也仅仅需要修改编组的定义,而不需要像传统的计算和建模方法那样,要对整个列车重新建模和修改程序,从而提高列车动力学仿真软件的通用性和灵活性.具体流程见文献[1]和文献[15].

2 长大线路建模与服役模拟计算技术

列车运行速度越高,车线耦合越强,考虑车线耦合的必要性就越大.关于车线耦合的研究特别多[16-25],耦合模型最具有代表性的是“翟孙”模型[17].然而,在传统的车线耦合动力学计算方法中,把钢轨简化成简支梁,并通过模态叠加方法,把连续梁变成以振动模态为广义变量的多体系统动力学系统,以实现车线耦合.这一方法的缺点是由于钢轨被简化成简支梁,如果钢轨(简支梁)长度太长,就要影响模态的空间计算精度,如果要反映出枕木(间隔通常为600 mm)间的钢轨振动,就必须考虑更高自振频率的模态,频率越高,计算误差越大.因此,文献[18]给出的方法,一是车辆在钢轨上不沿钢轨方向运动,仅仅是线路不平顺空间谱(条)向后运动来反映线路对车的激扰,但难以反映轨枕等线路结构带来的激扰;二是让车在有限的钢轨长度范围内运行,实现真正的车线耦合计算,模拟车辆前进运动,但线路长度有限,对高速列车而言,几秒钟就运行到头,系统振动难以被有效激发,难以反映真实的车线耦合振动,更无法模拟列车在更加复杂的长线路上运行的情况.

对于高速列车而言,在运行中会通过不同的线路,甚至是不同的交路.由于结构、地质状态、施工质量不一,列车在通过这些线路的响应也会不一样.图4 是实测的某一高速列车在不同线路的轴箱振动情况,显然在北京到杭州区段的振动小,车辆的动力学性能与线路状态强相关,在服役模拟时,首先需要知道不同线路的轨道不平顺谱.

当然,随着运行时间的增加,踏面的磨耗,轮轨关系恶化,轴箱的振动更加恶化,以至于需要车轮镟修来维持车轮状态,保持列车的动力学性能.因此,建立长距离线路的列车运行模拟是必要的,特别是在进行状态预测与评估时,更是要能真实反映其服役状态.

图4 某高速列车在不同线路运行的轴箱振动加速度响应Fig.4 Axle box vibration acceleration response of a high-speed train running on different tracks

2.1 关于滑移窗口

为了实现列车任意长线路的运行模拟,就必须有长大钢轨的建模与计算方法,显然是不应该简单把钢轨长度取长而损失模态空间计算精度,作者为此提出一种新的滑移窗口方法[1-3].滑移窗口模型可充分考虑离散轨下支撑特性和轨道不平顺的影响,尤其是线路沿纵向不均匀变化的支撑特性.此模型更加接近列车在轨枕跨间移动的实际情况.

在滑移窗口模型中,为满足高速铁路枕木、轨道板、和桥梁结构计算窗口的选择,滑移窗口长度lTW的设置是时变的,如图5 所示.滑移窗口设置的基本原则是:(1)针对枕木、轨道板和桥梁设置不同的计算窗口;(2) 窗口选择一是要保证有足够的长度,以保证窗口能反映振动的基本信息;(3)各窗口长度的设置要考虑到边界点,其中枕木(也就是钢轨) 窗口的设置长度一定在枕木上,不能在枕木中间,否则钢轨悬空、无法做计算边界点,轨道板的窗口边界一定在轨道板的边缘,桥梁的窗口也一定在桥梁端部,不能在轨道板和桥梁上面;(4)各窗口之间应该保持协调,也就是,轨道板窗口移动在桥梁窗口范围内,枕木(钢轨) 的窗口在轨道板的窗口内.根据以上滑移窗口设置的基本原则,则可确定不同线路类型对应的滑移窗口的长度.

滑移窗口是随车运行跳跃式移动(因此也可称之为“步进移动窗口”,由于窗口前进过程中,前后窗口大部分是重叠的,不是一个窗口接一个窗口,故作者建议称之为“滑移窗口”).对高铁而言枕木窗口的跳跃距离是枕木间距,一般为0.6 m,轨道板窗口的跳跃距离是轨道板长度,一般为6.5 m,高架桥梁窗口的跳跃距离是桥梁长度,一般为32 m,因此,各窗口移动一直在发生且交替变换,使计算变得十分复杂.为了简化,以桥梁窗口的移动为基础,轨道和枕木(钢轨) 窗口和桥梁窗口随动,但是,由于枕木和轨道板相对每一跨桥梁可能是不一致的,导致3 个窗口之间的相对位置有变换,而且桥梁本身跨距在不同位置也可能发生变化.因此,3 个窗口必须同时存在,按照上述规则进行协调移动.

考虑桥梁、轨道板和枕木及钢轨振动衰减,从而可以忽略所计算窗口外的振动.这时整个列车/线路的滑移窗口长度lTW,其与钢轨移动窗口长度lR,枕木移动窗口长度lS,桥梁移动窗口长度lB之间的关系应满足lR≤lS≤lB≤lTW.如果是路堤段无砟轨道,则没有桥梁窗口lB.

2.2 钢轨的滑移窗口计算方法

采用滑移窗口进行车线耦合计算时,由于枕木、轨道板和轨道桥可以看成离散的对象,因此移入移出计算窗口很好处理.但钢轨是一个连续体,即便是取一段钢轨作为梁单元进行计算,但之前还没有学者来尝试让钢轨通过滑移窗口,不断按照列车位置进行变化,实现任意长钢轨上的列车运行模拟.

假设在t0时刻,钢轨原计算窗口为AB,下一个计算时刻的窗口为A′B′,当然这时的钢轨有振动的位移(变形) 有效区在A′B之间的虚框内,虚框之外的钢轨振动位移可以忽略,如图6 所示.在窗口AB,钢轨假定为简支梁,A点为梁的局部坐标原点,沿轨道前进方向为x轴,这时的窗口AB梁的振动位移zr

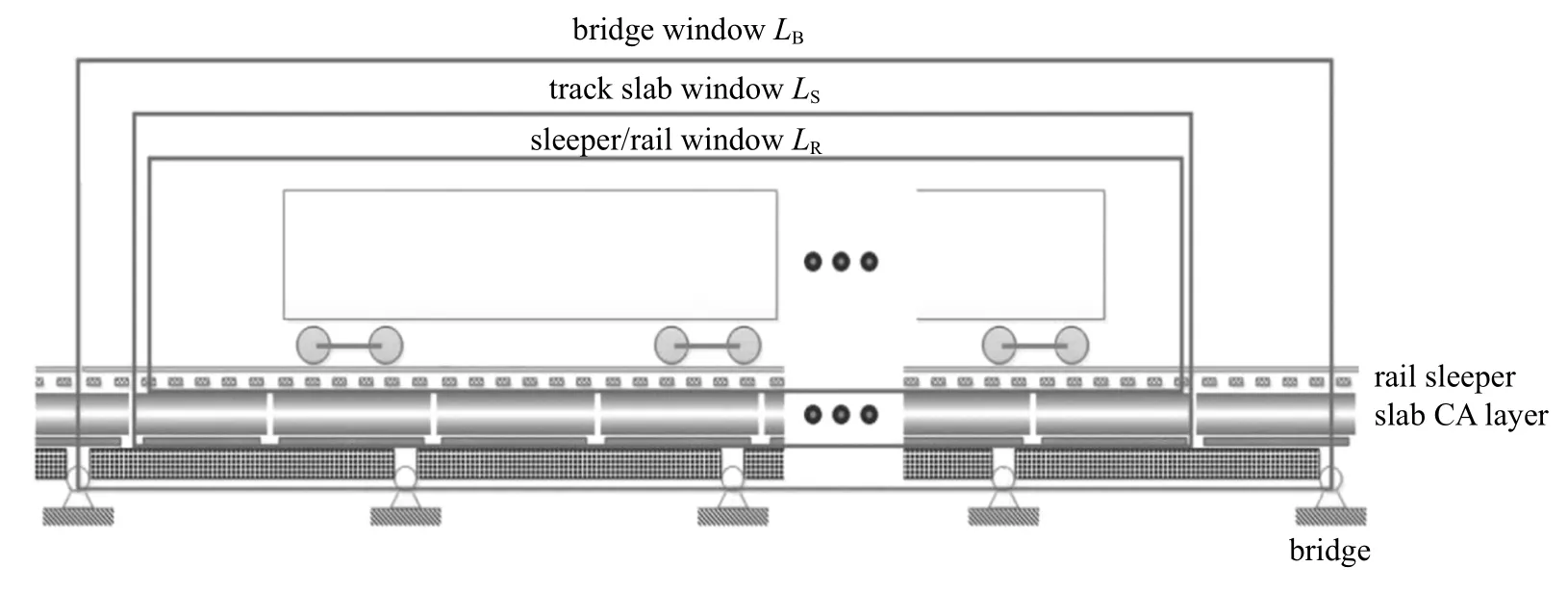
图5 滑移窗口长度计算模型Fig.5 Calculation model of sliding window length LS

图6 滑移窗口Fig.6 Sliding window

可以表述为下式

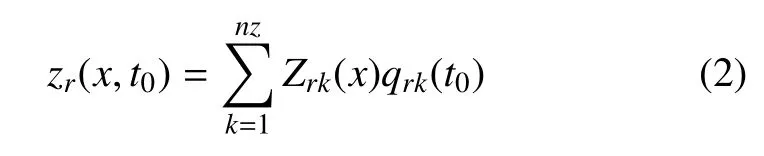
式中Zrk(x) 为窗口区钢轨AB的第k阶模态振型,qrk(t0)是第k阶模态幅值,nz是模态阶数.

在下一个计算时刻的窗口A′B′,钢轨假定为简支梁,A′点为梁的局部坐标原点,沿轨道前进方向为x′轴,这时的窗口A′B′梁的振动位移可以表述为下式

在下一个计算时刻的窗口A′B′,钢轨假定为简支梁,A′点为梁的局部坐标原点,沿轨道前进方向为x′轴,这时的窗口A′B′梁的振动位移可以表述为下式

在图7 中,A′B是前后两个计算时刻滑移窗口AB和A′B′的公共段,包含着钢轨的振动位移有效区.在公共段设置nz个断面,这样对于两个不同时刻窗口,同一个截面p处,钢轨在两个窗口坐标系中的坐标分别是(xp,zp)和由于是同一点,显然

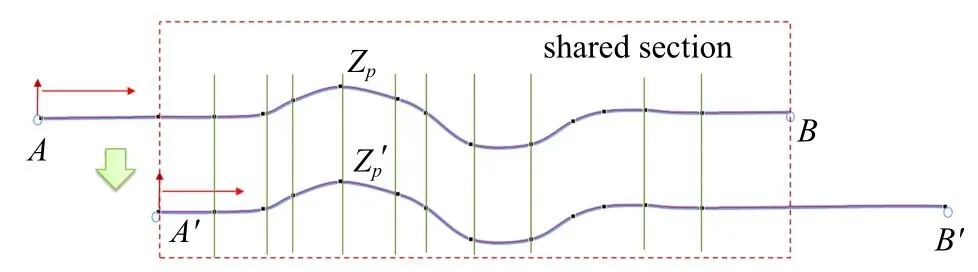
图7 滑移窗口断面设置Fig.7 Configuration of the sliding window section

由于,这时的钢轨振动位移zp和窗口A′B′的钢轨振型为已知量,式(3)就成为一个线性方程组,求解模态幅值当模态幅值求得后,这时的钢轨振动就从原窗口AB到新窗口A′B′,实现了窗口滑移.滑移窗口技术的应用,不仅可以有效降低长大线路仿真时的计算量,而且可以实现列车前进方式的仿真计算,同时可以比较灵活地处理路堤段、过渡段和桥梁段的复合结构线路方式,使得连续长大线路条件的列车运行仿真计算成为可能.这一方法的提出,已经被其他学者应用,认为是一种有效并高效的计算方法[26-28].

3 长期服役模拟

高速列车的设计寿命一般为25～30 年,期间要经过多次各种级别的维修,特别是到了四级修,大部分的零配件需要更换.影响整车动力学性能的悬挂元器件在长期使用中性能会慢慢退化,在三级修时需要检修,四级修时需要定期更换,以保障其动力学性能.

图8 是三级修和四级修对4 个抗蛇行减振器检测的结果,可以看到阻尼性能的退化.与此同时,车轮磨耗在运行过程中始终存在,随着磨耗,等效锥度等将产生变化(如图9 所示).此外,从图4 可以看到,当等效锥度超过0.35,振动明显加剧,最后导致失稳,必须通过车轮踏面镟修来保持踏面状态与轮轨关系.因此,在高速列车服役过程中,一、二系悬挂参数、踏面等效锥度等影响动力学性能的参数在服役过中不断发生变化,成为时变参数(或者是随距离变化参数).

图8 不同运行里程抗蛇行减振器特性Fig.8 Characteristics of yaw damper with different running mileage

图9 不同运行里程轮对等效锥度变化Fig.9 Equivalent conicity of wheelset with different running mileage

文献[29]第一次提出了基于高速列车耦合大系统的服役模拟问题,本文主要讨论高速列车动力学性能的服役模拟问题,给出图10 的服役模拟框图.首先是影响高速列车运行性能的边界和环境条件作为系统输入,包括线路的不平顺(反映出不同交路的线路状态)、环境风及地震波等;系统模型包括列车(车辆)模型与线路模型,车辆模型由质量、刚度与阻尼组成,包括车体、构架、轮对等质量块,一系与二系悬挂参数(刚度与阻尼),以及直接影响到车辆动力学性能的车轮踏面与钢轨廓形.一系与二系悬挂参数(刚度与阻尼),在服役过程中是可能变化的,可以把这些参数作为服役计算的时变参数,同时车轮踏面的磨耗以及钢轨的磨耗形成新轮轨关系,而真正影响车辆动力学性能的是轮轨匹配后的等效锥度状态,这也是目前判断车轮踏面是否需要镟修及钢轨是否需要打磨的依据.线路模型的结构参数(如扣件与钢轨垫板刚度)理论上也会变化的,但相对较慢,而且目前很难得到相关参数变化规律.因此,本文没有把线路结构参数作为时变参数处理,但可以根据列车运行的区段,考虑线路参数的差异性.在服役模拟的仿真计算中只要能考虑时变参数的变化,就可以得到不同服役条件下的列车动力学性能状态,如作者在文献[30-31]中的不同服役时间踏面磨耗状态下的车辆动力学性能预测.由于车轮踏面磨耗,车轮运用到20 万千米,横向平稳性恶化,最大平稳性指标达到3.19.这样预测结果作者在文献[31]图4-62 中得到实车测试验证,说明基于车轮踏面磨耗时变规律的车辆动力学预测的正确性.

事实上,悬挂参数的时变模型与服役的时间及车辆的振动状态密切相关,车轮踏面磨耗更是如此,可以通过长期的运用统计和研究,得到与服役时间及车辆振动状态相关的时变参数模型.在服役模拟时,根据车辆振动状态与服役时间,计算该运行时刻的时变参数值,据此进行新时刻的仿真计算,进而得到新时刻的车辆运动状态,从而实现高速列车长期的服役模拟.服役模拟不仅可以预测高速列车的动力学性能,掌握高速列车动力学性能的服役变化规律还可以为高速列车运行、维修和再设计提供依据.

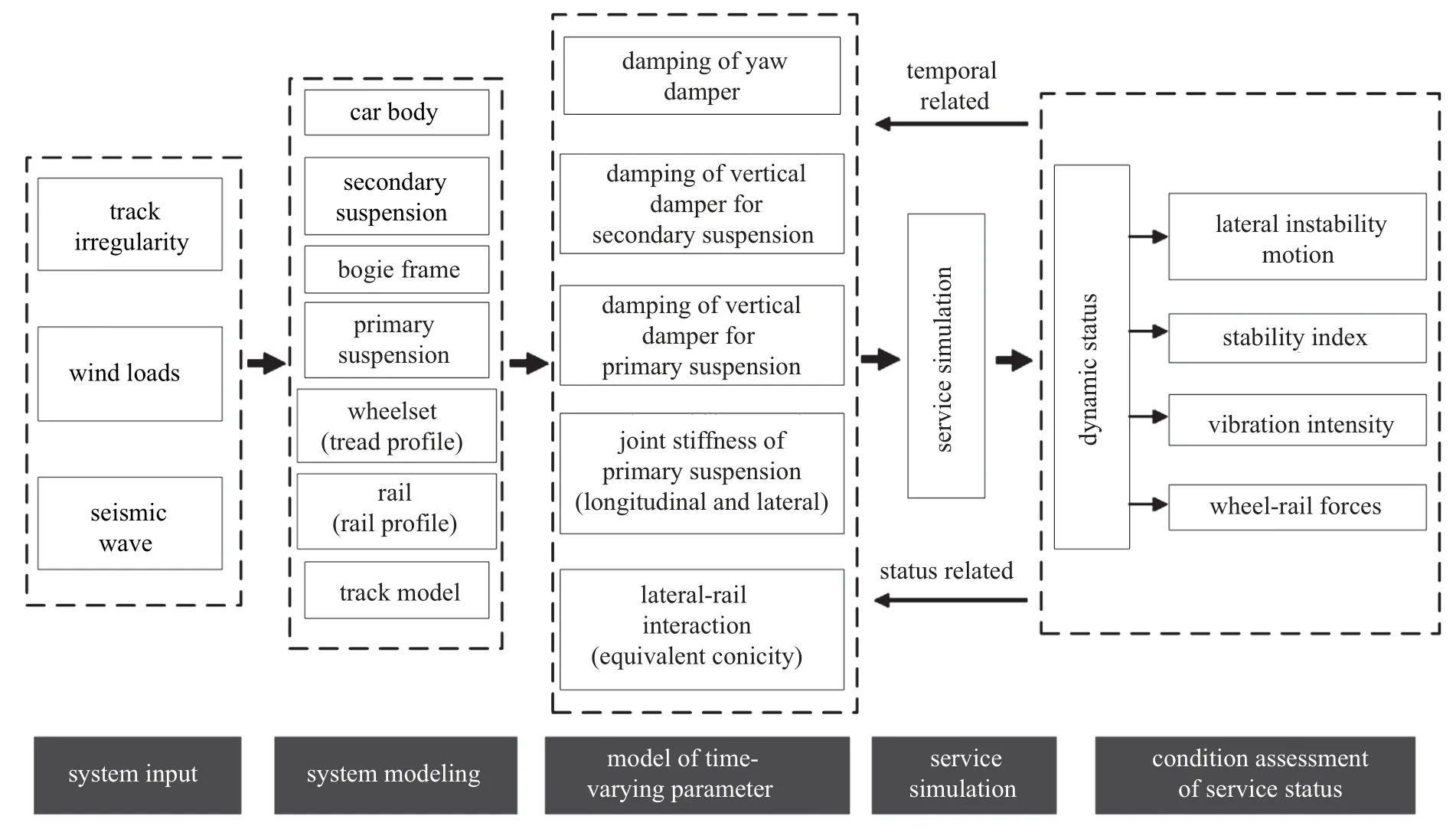
图10 基于动力学性能的服役模拟计算的框图Fig.10 Service simulation frame of high-speed train based on dynamic performance

4 结束语

车辆系统动力学仿真计算随着计算方法与计算手段的发展,越来越成熟.状态评估与状态修技术的发展,对高速列车系统动力学研究提出新的要求.作者针对长大编组、长大线路和长期服役的高速列车动力学问题,提出相应算法,一方面希望能实现任意编组形式列车在任意长线路上长期服役的运行模拟,为高速列车的设计、运行和维修提供研究手段;另一方面,是想推动传统的车辆系统动力学建模与计算方法的发展,完善作者所提出的高速列车耦合大系统动力学理论体系.随着运行速度的提高,系统间耦合加强,服役模拟也会越来越受到重视,包括在高速磁浮列车,甚至未来超高速真空管道磁浮列车中的应用.