如何正确运用χ2检验——χ2分布及相关内容

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在临床资料中，定性资料（特指结果变量及其取值）［1-6］出现的频率高。分析定性资料的统计分析方法主要有“差异性分析（通常适用于原因变量的个数≤2）［1-3］”和“logistic回归分析（通常被用于原因变量的个数＞2）［4-6］”两大类。在前述提及的两类统计分析方法中，“χ2检验”都是不可或缺的。

在经典统计学和贝叶斯统计学中，“概率分布”是统计分析的重要基础［7-11］，若离开了它，假设检验、区间估计、回归分析、判别分析和多元分析几乎无法进行。由数理统计知识可知，一旦掌握了某个随机变量的概率分布，就等于掌握了其变化规律。概率分布的种类很多，通常可以分为两大类，即“离散型随机变量的概率分布”和“连续型随机变量的概率分布”。本文介绍的χ2分布是在统计分析中被广泛使用的一个连续型随机变量的概率分布，它具有两种表现形式，即“χ2分布”和“非中心χ2分布”［10-11］。本文对χ2检验的基础知识，即“χ2分布及相关内容”进行介绍。

1 χ2分布

1.1 χ2分布的历史

χ2分布是从正态分布派生出来的一个连续型概率分布。尽管如此，由于许多分布可以用χ2分布来近似，甚至在多元统计分析中也常用到它，故χ2分布在数理统计中一直占有重要地位［11］。

χ2分布分别由 I.J.Bienayme（1858）、F.R.Helmert（1876）和K.Pearson（1900）发现，开始主要用于列联表资料的“独立性”分析和“评价回归模型对资料拟合效果好坏”的拟合优度检验［12］；在定性资料回归模型的构建过程中，χ2分布常用于筛选自变量［13］；在广义线性回归模型和混合效应回归模型的构建中，χ2分布常用于两个回归模型对同一个资料拟合效果的比较［13］。

1.1.1χ2分布的定义

设随机变量Y1，Y2，…，Yn独立同分布，且Yi～N（0，1），则随机变量的分布称为具有n个自由度的χ2分布，并记为。见式（1）：

1.1.2χ2分布的概率密度函数及其图形

χ2分布概率密度函数的图形见下图：

1.1.3χ2分布的性质

1.1.3.1χ2分布的极限分布为正态分布

由图1可看出如下特点：①自由度n越大，曲线越趋于对称；②当自由度n→∞时，χ2分布趋向于正态分布。

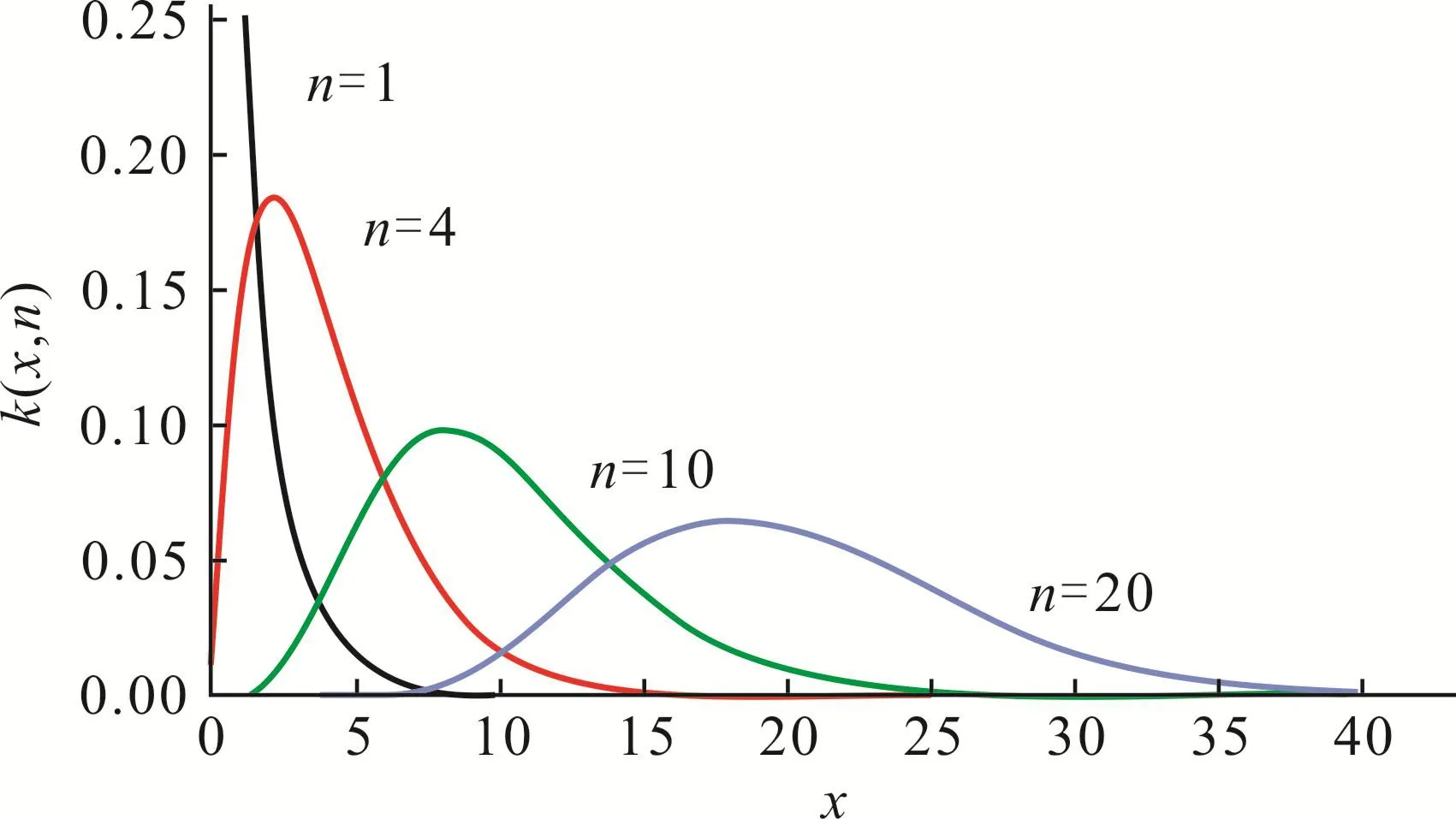
图1 具有几种不同自由度的χ2分布概率密度函数的图形

1.1.3.2χ2分布的期望和方差

式（4）的“E”代表“期望（通俗的表述为‘均值’）”；“Vɑr”代表“方差”。

1.1.3.3χ2分布具有可加性

1.2 非中心χ2分布

1.2.1 非中心χ2分布的定义

设随机变量Y1，Y2，…，Yn相互独立，且Yi～N（μi，1），则随机变量的分布称为具有n个自由度且非中心参数为的χ2分布，并记为见式（6）：

在上式中，当δ=0时，非中心χ2分布就退化成为前面定义的χ2分布χ2n。

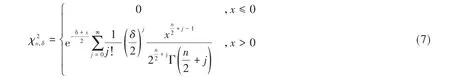
【说明】因篇幅所限，该分布的性质从略。

2 χ2分布与正态分布之间的关系

χ2分布是从正态分布派生出来的一个分布；χ2分布的极限分布为标准正态分布［7，11］。用数学语言表述如下：

若Xn～，n=1，2，…，则当n→∞时，有下面的关系式成立：

另一方面，由来自正态分布的均值与离均差平方和或方差可构造出服从χ2分布的随机变量。事实上，若X1，X2，…，Xn（n≥2）是从总体N(μ，σ2)中抽出的样本，令：

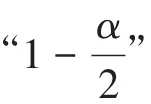
3 χ2检验统计量与Z检验统计量之间的关系

由本文式（1）定义的χ2分布可知，它是由n个互相独立且都服从标准正态分布的随机变量的平方之和构成的，故当其自由度为1时，χ2检验统计量的平方根就是Z检验统计量（说明：在SAS软件和部分统计学教科书中，通常用Z表示服从标准正态分布的随机变量或检验统计量）。

4 χ2分布的计算

4.1 χ2分布曲线下累计概率的计算

在SAS软件中，χ2分布的分布函数为：

probchi（x，df，nc）

该函数计算服从自由度为df，非中心参数为nc的χ2分布的随机变量小于给定x的事件的概率。如果nc没有规定或取为0，那么被计算的就是中心χ2分布曲线下累计概率。

【例1】试计算自由度为5，中心χ2分布曲线下χ2值小于20的概率值。

【分析与解答】所需要的SAS程序如下：

以上结果表明，当χ2=20、自由度df=5、非中心参数nc=0的条件下，χ2分布曲线下且位于横坐标轴上“0～20”区间内的累计概率为0.99875。

4.2 χ2分布曲线下横坐标轴上P分位数的计算

在SAS软件中，χ2分布的分位数函数为：

cinv（P，df，nc）（0≤P≤1，df＞0，nc≥0）

该函数计算自由度为df，非中心参数为nc的χ2分布的P分位数。取nc=0或不规定此项参数时，表明是中心χ2分布。

【例2】试计算自由度为3，非中心参数为4.5的χ2分布的P=0.95的分位数。

【分析与解答】所需要的SAS程序如下：

以上结果表明，当累计概率P=0.95、自由度df=3、非中心参数nc=4.5的条件下，χ2分布曲线下横坐标轴上的分位数x=16.8463（注意：这里的“x”是一个服从自由度df=3、非中心参数nc=4.5的χ2分布的随机变量）。

【例3】试基于SAS函数“cinv（P，df，nc）”产生χ2分布临界值表。

【分析与解答】在很多统计学教科书的附录中，一般都会给出常用统计用表，其中，χ2分布临界值表可以利用SAS函数“cinv（P，df，nc）”且令nc=0计算出来。现给出所需要的SAS程序如下：

【程序说明】“D O d=1 T O 4 0，5 0，6 0，7 0，8 0，9 0，100”语句表明，自由度df的取值为1、2、…、39、40、50、60、70、80、90、100，共46种取值，即产生的χ2分布临界值表有 46 行；“alpha=0.995，0.990，0.975，0.950，0.900，0.750，0.500，0.250，0.100，0.050，0.025，0.010，0.005；p=1-alpha；”两个语句表明，χ2分布曲线下右侧尾端概率分别为0.995、0.990、…、0.005，共13种取值。也就是说，以上SAS程序共计算出46×13=498个χ2分布临界值（本质上就是χ2分布曲线下横坐标上的“分位数”的数值）。

【说明】因输出的数据较多，此处从略。

5 讨论与小结

5.1 讨论

χ2分布是一种连续型随机变量的概率分布，然而，它不同于其他连续型随机变量的概率分布（如“正态分布”等）。因研究者应用统计学的过程中，诸如“正态分布”“t分布”和“F分布”的连续型概率分布常作为“Z检验”“t检验”和“方差分析（或称F检验）”的理论依据，直接应用于定量资料的差异性分析；而χ2分布作为“χ2检验”的理论依据，一般只应用于定性资料的差异性分析（如各种列联表资料的差异性分析）、不同统计模型对同一个统计资料拟合优度的比较等场合。但也有例外，即χ2检验可应用于单因素多水平设计一元定量资料多个方差的齐性检验之中。χ2分布和χ2检验之所以可以应用于前述提及的各种场合，因为在那些场合下所构造出的“检验统计量”服从χ2分布。

5.2 小结

本文针对处理定性资料所需要的χ2检验，介绍了与其有关的理论基础，即χ2分布和非中心χ2分布。重点展示了χ2分布的定义、概率密度函数的图形和主要性质；基于SAS软件中的两个SAS函数呈现了χ2分布的计算方法（包括累计概率的计算和分位数的计算）和结果解释。

科研方法专题策划人——胡良平教授简介

胡良平，男，1955年8月出生，教授，博士生导师，曾任军事医学科学院研究生部医学统计学教研室主任和生物医学统计学咨询中心主任、国际一般系统论研究会中国分会概率统计系统专业理事会常务理事、中国生物医学统计学会副会长、北京大学口腔医学院客座教授和《中华医学杂志》等10余种杂志编委；现任世界中医药学会联合会临床科研统计学专业委员会会长、国家食品药品监督管理局评审专家和3种医学杂志编委；主编统计学专著48部、参编统计学专著10部；发表第一作者和通信作者学术论文300余篇、发表合作论文130余篇；获军队科技成果和省部级科技成果多项；参加并完成三项国家标准的撰写工作、参加三项国家科技重大专项课题研究工作。在从事统计学工作的30年中，为几千名研究生、医学科研人员、临床医生和杂志编辑讲授生物医学统计学，在全国各地作统计学学术报告100余场，举办数十期全国统计学培训班，培养20多名统计学专业硕士和博士研究生。近几年来，参加国家级新药和医疗器械项目评审数十项、参加100多项全军重大重点课题的统计学检查工作。归纳并提炼出有利于透过现象看本质的“八性”和“八思维”的统计学思想，独创了逆向统计学教学法和三型理论。擅长于科研课题的研究设计、复杂科研资料的统计分析和SAS与R软件实现、各种层次的统计学教学培训和咨询工作。