指数分布基于波动率的异常数据检验*
邱小蓝,李云飞
(西华师范大学数学与信息学院,四川 南充637002)
1 引言
如今处于信息社会,在科学技术研究领域中人类面对的问题日益复杂。在这些研究过程中,最重要的问题是如何有效地收集、分析和处理包含大量信息的试验数据。然而,由于种种原因,在实际研究工作中,学者们获得的试验数据中会存在一些异常数据。所谓异常数据,是指一批数据中的个别值,其数值明显偏离它或它们所属的这批数据的其余观测值[1]。异常数据的存在会增大分析结果的误差,使一些经典的统计分析方法变得毫无用处,甚至导致整体决策上的失误,造成无法估计的损失。因此,如何检验这些异常数据是一个重要的现实问题。
许多统计工作者针对不同的分布(正态分布、极值分布、双参数Weibull 分布等)中的异常数据检验问题进行了深入的研究[2-8]。然而,针对可靠性理论中的一种重要分布——指数分布相关的异常数据检验研究不多。指数分布是描述电子系统、产品寿命的模型,它不但在电子元器件,机电产品的偶然失效期内普遍使用,而且在复杂系统和整机方面以及机械技术的可靠性领域也得到广泛应用[9]。因此,指数分布中异常数据的检验问题很重要,具有理论意义和现实价值。
FⅠSHER[10]提出构造统计量分别检验样品极值X(1)、X(n)是否为异常数据。KⅠMBER[11]提出利用同时检验X(1)、X(n)是否为异常数据。在KⅠM B E R 的基础上,唐年胜等[12]提出利用分别检验X(1),…,X(s)和X(n-k+1)是否为异常数据。基于FⅠSHER 的统计量,朱宏[13]提出基于样本中位数构造统计量和分别检验样本极值X(1)、X(n)是否为异常数据。李云飞[14]提出基于样本分位数构造统计量,可以通过分别检验样本极值X(1)、X(n)是否为异常数据。
本文在王蓉华等[15]提出的均值比检验方法的基础上,引入波动率[16]的概念,构造检验统计量,给出一种新的检验方法,用于检验指数分布的异常数据。
2 度量标准
记X1,X2,…,Xn是来自于指数分布总体X的样本,其分布函数为:

假定x1,x2,…,xn是样本X1,X2,…,Xn的观测值,将x1,x2,…,xn按照从小到大的顺序排列,得到x(1)≤x(2)≤…≤x(n),即是样本X1,X2,…,Xn的次序统计量X(1),X(2),…,X(n)的观测值[9],如果样本中存在异常数据,则一定会出现在X(1),X(2),…,X(n)的左侧低端或右侧高端。
设X(1),X(2),…,X(r)(1≤r≤n)是来自指数分布的样本容量为n的前r个次序统计量,平均寿命参数μ=θ,可以得到θ的最小方差无偏估计,即是MLE 为:

定义1[15]:设X(1),X(2),…,X(r)(1≤r≤n)是来自总体分布F(x,θ)的样本容量为n的前r个次序统计量,是仅依赖于X(1),X(2),…,X(k)的均值μ的点估计,称是均值点估计 ˆkμ在点k的跳跃度(简称k点的跳跃度)。
由于点估计的跳跃度可能存在负数值,故在跳跃度的基础上提出波动率的概念,进而由此衡量异常数据对点估计的影响。同样假设X(1),X(2),…,X(r)(1≤r≤n)是来自总体分布F(x,θ)的样本容量为n的前r个次序统计量, ˆkμ是仅依赖于X(1),X(2),…,X(k)的均值μ的点估计,称为X(k)对均值μ的点估计的波动率(简称k点的波动率)[16]。
以下讨论跳跃度的精确分布及其分位数。
引理1[17]:设X1,X2,…,Xn是来自于指数分布的样本容量为n的样本,X(1),X(2),…,X(r)(1≤r≤n)为前r个次序统计量。约定X(0)=0,令Y(1)=nX(1),Y(2)=(n-1)(X(2)-X(1)),…,Y(i)=(n-i+1)(X(i)-X(i-1)),…,Y(r)=(n-r+1)(X(r)-X(r-1)),(2)。则…,r;2°Y(i)相互独立,i=1,…,r。
定理1[15]:设X(1),X(2),…,X(r)(1≤r≤n)是来自指数分布的样本容量为n的前r个次序统计量,则对任意的1≤k<r≤n,有分布的1-α分位数,其中,F1-α(2(r-k),2k)是自由度为2(r-k),2k的F-分布的1-α分位数。
3 异常数据检验步骤
异常数据的检验通常有以下2 种检验方法:①从整体出发,利用检验统计量逐步检验异常数据;②利用某种方法,即根据一定规则先找出可疑的异常数据集合,而后用合适的检验统计量来检测这个集合是否异常[16]。第一种方法由于统计量的选取不当,很容易遭受屏蔽效应或吞噬效应,而不易确定异常数据个数是第二种方法的弊端。本文将采用完全相反的方式,利用王蓉华[15]的均值比方法,首先按照相应的准则找出有序数列的正常数据集,随后从正常数据集出发,每次向左或向右添加一个相邻数据,用合适的检验统计量来检测是否为异常数据,如此下去,直至找到所有的正常数据。以下介绍检验步骤。
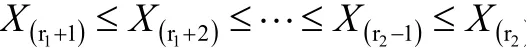

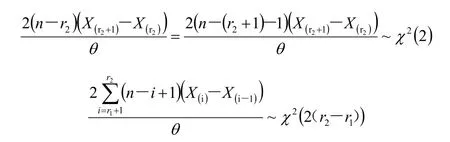
以上两者相互独立,由定理1 可知:

显然,对于给定的显著性水平α(0.10,0.05,0.01),如果,则可以认为是异常大数据。如果,则认为在显著性水平α下,是异常大数据, 也是最小的异常大数据, 从而认为都是异常大数据;否则,则继续添加下一个数据,进行考察:
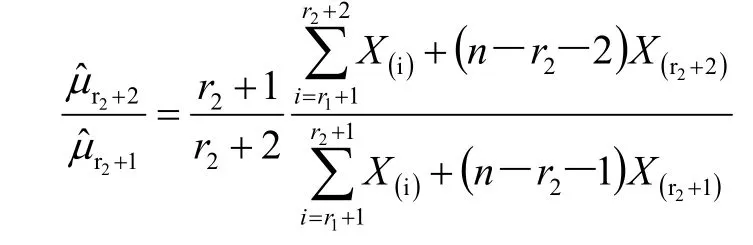
如上述方法步骤重复进行,直至找到最小的异常大数据,那么该数据后面的所有数据都为异常大数据。在剔除所有的异常大数据后,在正常数据的左侧低端依次添加数据来检验是否为异常小数据,显然,后面的检验步骤和检验异常大数据的步骤完全相似。在找到最大的异常小数据后,则该数据以前的所有数据都为异常小数据。在剔除所有的异常小数据后,得到的数据就为来自指数分布的正常样本数据。
4 实例分析
本文仅对只存在异常大数据的样本进行实例分析。案例[15]:对指数分布取n=10、k=6,其中X(1),…,X(6)来自标准指数分布,X(7),…,X(10)来自参数θ=5 的指数分布,用Monte-Carlo 模拟的方法产生这10 个随机数为0.079 9、0.136 3、0.279 3、0.423 1、0.617 9、0.921 2、4.821 6、5.833 6、8.549 4、13.059 9。
首先计算各点的波动率如下(2≤k≤10):0.182 6、0.250 4、0.058 2、0.070 4、0.106 4、2.034 3、0.002 8、0.083 7、0.034 2。
从中可以看出在ξ(7)=2.034 3 点波动率最大,为一极大值点,所以X(7)、X(8)、X(9)、X(10)极其可能是异常大数据,由于,所以,取1-α=0.95,枢轴量的分位数U,由此可确定X(7)为最小的异常大数据,进而确定是异常大数据。
5 总结
异常数据的出现在一定程度上降低了数据的质量,使相应的数据分析结果发生明显变异,最终导致人们对所分析的问题给出不正确的结论,因此,异常数据的检验是统计分析中首要的工作[18]。
本文针对指数分布样本中的异常数据,在跳跃度[15]的基础上,引入波动率的概念,构造检验统计量,并给出相应的精确分布,求出它的分位数,给出了一种新的异常数据检验方法,最后通过实例说明本文所讨论的方法是实际可行的。

