人才集聚、科技创新与经济高质量增长的交互效应——基于省级面板数据VAR模型的实证分析

王黎明，王 宁

(山东理工大学 经济学院，山东 淄博 255012)

一、引 言

人才是经济社会转型和发展中最活跃的智力资源，同时也是衡量区域经济发展和技术创新竞争力的重要指标。科技创新是建设现代化经济体系的战略支撑，科技型人才集聚对经济高质量发展具有一定的推进作用。党的十九大报告进一步明确了创新在引领经济社会发展中的重要地位，作为经济发展的战略支持，人才又是创新的能动力量。因此，如何以人才作为发展引擎，提升区域科技人才的存量和集聚水平，促进经济高质量发展具有重要的研究意义。本文在之前学者的研究基础上，以三者互为因变量，研究彼此之间的影响，选取了中国31个省(直辖市、自治区)的样本数据(考虑数据可得性等问题，暂未包括港澳台地区)，研究人才集聚、科技创新与经济增长三者之间的交互作用及滞后影响，为制定相关政策提供参考。

二、文献回顾

(一)人才集聚与经济增长

早在1960年，舒尔茨就提出资本应该分成物质资本和人力资本，其中人力资本指的是通过对人力的投资而形成的资本，并且认为教育可以增加人力资本(1)西奥多·W.舒尔茨:《论人力资本投资》，吴珠华译，北京经济学院出版社，1990年，第99页。。Danilo Guaitoli研究了物质资本和人力资本以及内生增长之间的关系，该研究显示了人力资本对人均GDP增长率与收入分配不平等的作用机制(2)Danilo Guaitoli,Human Capital Distribution,Growth and Convergence,Research in Economics,2000.。刘瑞翔等选取了全国31个省级行政区五年的相关变量数据，研究表明各省的人口城市化率以及人力资本水平的提高对于该省域的经济增长质量具有明显的促进作用，但是对周边省份具有反作用(3)刘瑞翔,夏琪琪：《城市化、人力资本与经济增长质量：基于省域数据的空间杜宾模型研究》,《经济问题探索》，2018年第11期。。贺勇等也测算过人才集聚对我国区域经济增长的作用，认为人才集聚水平较高的区域，其对经济增长的贡献也较高，但两者之间并不具有严格的正向关系(4)贺勇，廖诺,张紫君：《我国省际人才集聚对经济增长的贡献测算》,《科研管理》，2019年第11期。。

(二)人才集聚与科技创新

修国义提出科技人才集聚规模和均衡度与区域科技创新效率显著正相关，强度与区域科技创新效率显著负相关(5)修国义，韩佳璇，陈晓华：《科技人才集聚对中国区域科技创新效率的影响：基于超越对数随机前沿距离函数模型》,《科技进步与对策》，2017年第19期。。刘晔等采用微观数据，寻找与我国区域创新水平有关的因素，认为仅在创新产出水平高的区域，科研人才知识的吸收能力对于某些创新投入要素起到正向调节作用(6)刘晔等：《科研人才集聚对中国区域创新产出的影响》,《经济地理》，2019年第7期。。赵青霞等通过对科技人才集聚、产业集聚及其交互作用对区域创新能力的影响研究，发现科技人才集聚水平较高的地区，需要结合高密度的产业集聚，可以提升区域创新能力(7)赵青霞，夏传信，施建军：《科技人才集聚、产业集聚和区域创新能力：基于京津冀、长三角、珠三角地区的实证分析》,《科技管理研究》，2019第24期。。葛雅青应用空间分析法，通过对我国30个省份国际人才的研究，得出国际人才数量每增加1%，区域专利数增长0.23%的结论(8)葛雅青:《中国国际人才集聚对区域创新的影响：基于空间视角的分析》,《科技管理研究》，2020第6期。。

(三)科技创新与经济增长

徐佳楠等认为科技金融投入与科技创新的经济增长效应均存在门槛效应，当二者协同发展时，才能更好地发挥对经济增长的促进作用(9)徐家楠,徐旭初:《科技金融投入、科技创新与经济增长》,《南京航空航天大学学报》(社会科学版)，2020年第3期。。辛璐等研究了科技创新对经济增长的滞后效应，研究结果表明，科技创新对经济增长在滞后1～2年具有促进作用(10)辛璐,罗守:《科技创新促进经济增长的滞后效应研究：基于省际面板数据的检验》,《管理现代化》，2020年第3期。。阎东彬通过实证研究，认为京津冀地区的科技创新有助于推动经济增长，但科技创新对经济发展的加速器作用还未充分显现(11)阎东彬:《科技创新与经济增长关系的实证：以京津冀城市群为例》,《统计与决策》，2020年第2期。。刘红等研究了金融创新及技术创新对陕西省经济增长的作用，发现技术创新投入或产出对经济增长具有双向影响(12)刘红,温军,张森:《金融创新、技术创新与经济增长的嵌合驱动：以陕西省为例》,《统计与决策》，2020第2期。。

(四)人才集聚、科技创新、经济增长三者之间关系

徐彬等认为人才集聚、创新驱动对经济发展的影响存在滞后效应，并且认为人才集聚带来的创新效应可能会外溢(13)徐彬,吴茜:《人才集聚、创新驱动与经济增长》,《软科学》，2019年第1期。。葛李情等研究表明，人才集聚与科技创新分别在不同程度上拉动了中国经济增长，经济增长吸引了人才集聚，人才集聚水平促进了科技创新(14)葛李情,胡昊:《人才集聚、科技创新与经济增长》,《福建商学院学报》，2019第5期。。

综上所述，目前我国对人才集聚、科技创新与经济增长的研究大多以单一指标为因变量研究当期影响。很少关注到三者间的交互作用及长期的滞后影响。但实际上，经济增长、人才集聚与科技创新并不只与单一指标有关，也并不只局限于当期影响，为了全方位考察各个指标，本文以三者互为因变量，研究彼此之间的影响，首先应用固定效应模型分析三者间的交互效应，又采用了面板数据VAR(PVAR)模型分析，PVAR模型是向量自回归模型，即用模型中所有当期变量对所有变量的若干滞后变量进行回归分析，关注了人才集聚、科技创新与经济增长之间的滞后效应。

三、变量选取与数据分析

(一)变量选取

为考察人才集聚、科技创新与经济增长之间的关系，本文将经济增长水平、人才集聚水平、科技创新水平作为模型的解释变量，首先对面板数据进行固定效应回归分析，再采用面板数据PVAR模型分析变量之间的因果关系与影响程度以及滞后效应。

(1)经济增长量(EG)。经济增长量采用人均GDP来衡量，为了便于计算，将人均GDP进行对数处理，公式如下：

EG=LN(GDPpc)

(1)

(2)人才集聚水平(TAL)。该指标采用各省就业人员的受教育程度来衡量，由于数据选取1998-2017年的受教育程度，考虑数据可得性，选取其中大专及以上就业人员的构成比例来当作衡量人才集聚水平的指标，用TAL来表示，其中2000年就业人员受教育程度的数据部分缺失，根据线性插值法补全。

(3)科技创新水平(TIL)。在衡量科技创新的指标时，Alfranca等(15)Alfranca O,Huffman W E,Aggregate private R&D Investments in Agriculture:the Role of Incentives,Public Policies,and Institutions.Economic Development and Cultural Change, 2003.、Acemoglu等(16)Acemoglu D,Akcigit U,Intellectual Property Rights Policy,Competition and Innovation.Journal of the European Economic Association,2012.采用研发经费(R&D)作为输入变量，Kim等(17)Kim Y K,Lee K,Park W G,et al,Appropriate Intellectual Property Protection and Economic Growth in Countries at Different Levels of Development.Research Policy, 2012.又把R&D在地区生产总值(GDP)中的占比作为输入变量，Fang等(18)Fang L H,Lerner J,Wu C,Intellectual Property Rights Protection,Ownership,and Innovation:Evidence from China.The Review of Financial Studies, 2017.采用R&D在企业总资产中的占比作为输入变量。在2005年，Hu等(19)Hu M C,Mathews J A. National Innovative Capacity in East Asia.Research Policy, 2005.、Schneider(20)Schneider P H. International Trade,Economic Growth and Intellectual Property Rights:a Panel Data Study of Developed and Developing Countries.Journal of Development Economics,2005.、Chen等(21)Chen Y,Puttitanun T,Intellectual Property Rights and Innovation in Developing Countries.Journal of Development Economics, 2005.将专利申请量看作创新输出变量，有学者将产品销售量、产品质量的提升等作为创新输出变量。基于已有学者的研究成果及考虑到数据的可获得性，本研究选择了全国除港澳台地区之外的专利实际授权数作为衡量科技创新水平的指标，采用专利的实际授权数更能体现一个地区的科技创新水平。为了模型的平稳，这里将科技创新水平用专利授权数量取自然对数来表示。

(二)变量的描述性统计

本研究以中国31个省份(除港澳台地区)的经济增长水平(EG)、人才集聚水平(TAL)、科技创新水平(TIL)为研究对象，选择1998-2017年的数据，建立面板数据模型。其中经济增长水平和科技创新水平数据来源于1999-2018年《中国统计年鉴》。人才集聚水平数据来源于1999-2018年的《中国劳动统计年鉴》，三个变量的描述统计如表1所示。由表1可以看出，全国(除港澳台)经济增长水平(EG)、人才集聚水平(TAL)与科技创新水平(TIL)每类指标的最大值最小值都有很大的差距，也体现了三个变量在全国各省间发展的不均衡，在时间跨度上，从1998年到2017年各变量的水平也发生了很大的改变。

表1 相关变量的统计性描述

四、实证模型及结果分析

(一)面板数据的单位根检验

为了防止检验结果出现伪回归现象，模型的建立首先要求各变量均平稳，所以在对数据进行回归之前，必须对各变量数据的平稳性进行单位根检验，如果变量序列不平稳，则可能使模型的估计结果出现偏差。所以本研究采用了LLC检验法、IPS检验法以及ADF检验法对三个变量分别进行单位根检验，经济增长水平(EG)、人才集聚水平(TAL)、科技创新水平(TIL)的原始序列在个别检验方法下皆为不平稳序列，经过差分后均处于平稳状态，此时可以对数据进行下一步分析检验，单位根检验结果如表2所示。

表2 全国3个指标变量的检验结果

(二)面板数据估计结果

首先确立基本回归方程，根据选取变量确立回归方程如下：

EG=c0+c1TAL+c2TIL

(2)

TAL=c0+c1EG+c2TIL

(3)

TIL=c0+c1EG+c2TAL

(4)

对三个公式分别进行估计，经hauseman检验，以99%以上的概率接受拒绝随机效应的原假设，说明三个模型均采用固定效应模型为最佳选择。所以三个模型均采用固定效应模型进行估计，估计结果如表3所示。

表3 面板数据估计结果

公式(2)的估计模型拟合优度为0.9058，考察人才集聚及科技创新对经济增长的影响，所有变量皆在1%的置信水平下通过了统计检验。从弹性系数来看，科技创新水平(TIL)弹性系数为0.637，高于人才集聚水平(TAL)的弹性系数0.012，说明科技创新水平和人才集聚水平对经济增长的正向作用前者更大，即科技创新水平每增加1%，经济增长0.637%;人才集聚水平每增加1%，经济增长0.012%。相较于科技创新水平，人才集聚对经济增长的推动力有限。

公式(3)的估计模型拟合优度为0.7186，主要用来估计经济增长及科技创新对人才集聚的影响，所有变量皆在1%的置信水平下通过了统计检验。从弹性系数来看，经济增长(EG)弹性系数为2.096，科技创新(TIL)的弹性系数3.187，说明经济增长和科技创新对人才集聚起正向作用，经济增长每增加1%，人才集聚增长2.096%；科技创新每增加1%，人才集聚增长3.187%。

同上，公式(4)的估计模型拟合优度为0.9133，主要用来估计经济增长及人才集聚对科技创新的影响，所有变量皆在1%的置信水平下通过了统计检验。从弹性系数来看，经济增长(EG)弹性系数为1.098，人才集聚(TAL)的弹性系数0.032，说明经济增长和人才集聚对科技创新起正向作用，即经济增长每增加1%，科技创新增长1.098%；人才集聚每增加1%，科技创新增长0.032%。

(三)滞后阶数确定及模型稳定性检验

PVAR模型由Holtz-Eakin 首次提出，这种模型在保留VAR模型优点的前提下，加入了新的内容，也就是既能体现出变量之间的互相冲击，又引入个体效应，表现出每个变量的变动对自身变化的影响，而且在时间序列的基础上加入了面板数据的情况(22)Douglas Holtz-Eakin,Whitney Newey,Harvey Sirosen.Estimating Vector Autoregressions with Panel Data,Econometrica,1988.。在进行脉冲响应及方差分解之前要进行滞后阶数的确定，在滞后阶数选取时，根据 AIC 准则，经过多次尝试后确定最优滞后阶数为3阶，因而三变量的回归方程可表述为:

yit=αi+βt+Ayit-1+βyit-2+Cyit-3+εit,i=1，…，31；t=1,…,20

(5)

式(5)中，yit={EG,TIL,TAL}是一个包含 3 个因变量的向量， A、B、C 均为系数矩阵，也就是本文的待估参数。与 VAR模型相比， PVAR 模型引入了个体效应αi。

在进行PVAR脉冲响应及方差分解之前，应该对模型稳定性进行检验，来判别模型整体的稳定性，模型稳定结果如图1所示，三个变量中，所有特征根皆小于1，位于单位圆内，说明模型是稳定的，此时，可以继续进行脉冲响应及方差分解。

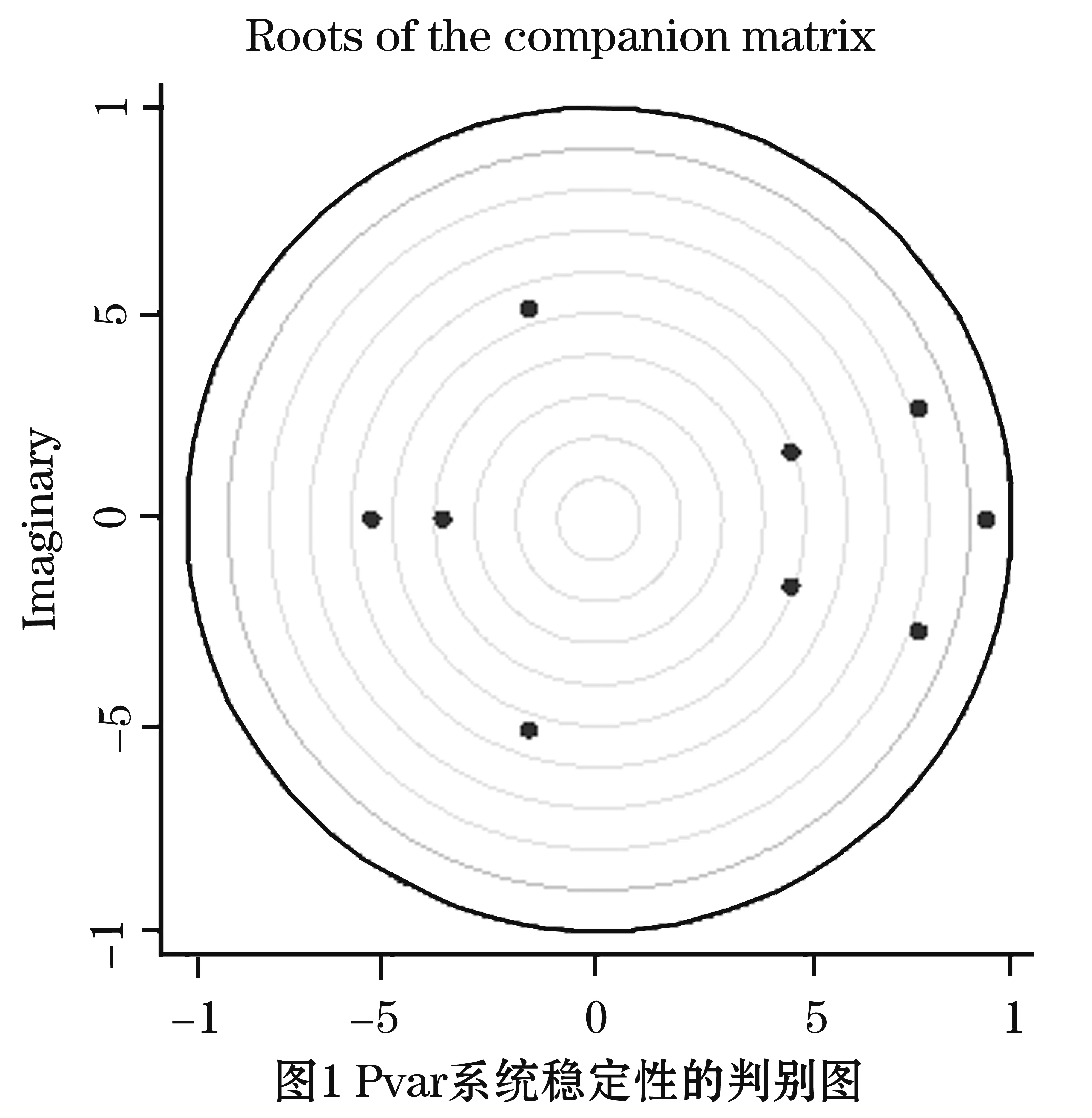
在确定了滞后阶数和模型稳定性判别之后，又对三个变量进行了格兰杰因果检验，格兰杰因果关系检验主要用于分析各变量之间是否存在因果关系，由此来判断接下来的脉冲响应及方差分解是否有意义。若格兰杰检验不通过，则说明三者之间并不存在显著的因果关系，继续进行脉冲响应或方差分解都没有意义。格兰杰检验结果如表4所示，由Prob值可以看出，经济增长(EG)、人才集聚(TAL)以及科技创新水平(TIL)三者之间有着显著的因果关系，可以进行下一步分析。

表4 格兰杰因果检验

(四)脉冲响应及方差分解

对三个变量的固定效应回归分析及一系列检验之后，我们继续对三个变量进行脉冲响应以及方差分解，图2为经济增长水平(EG)、人才集聚水平(TAL)与科技创新水平(TIL)的脉冲响应及方差分析结果，其所示脉冲响应结果表明，人才集聚对自身的驱动效应主要体现在滞后1期，产生了正向效应之后马上恢复了平稳。科技创新水平对人才集聚不仅在当期显示了显著的正效应，在滞后几期依然存在着脉冲响应。经济增长水平对人才集聚水平的冲击却比较复杂，首先在1、2期表现出的是一个负向冲击，这可能是由于经济增长吸引人才集聚导致的集聚水平的分母变大，比值变小，从而导致滞后1、2期产生了负效应，但随后在第3期负效应逐渐减弱，到第4期表现出正向冲击，逐渐回归平稳且效应依然为正。科技创新及经济增长对自身的冲击与人才集聚的自身冲击曲线类似，都是在滞后1期有正向冲击，到2、3期恢复平稳；而经济增长水平对科技创新水平是在第2期产生正向冲击又恢复平稳的。其他变量之间的滞后脉冲响应相对平稳。

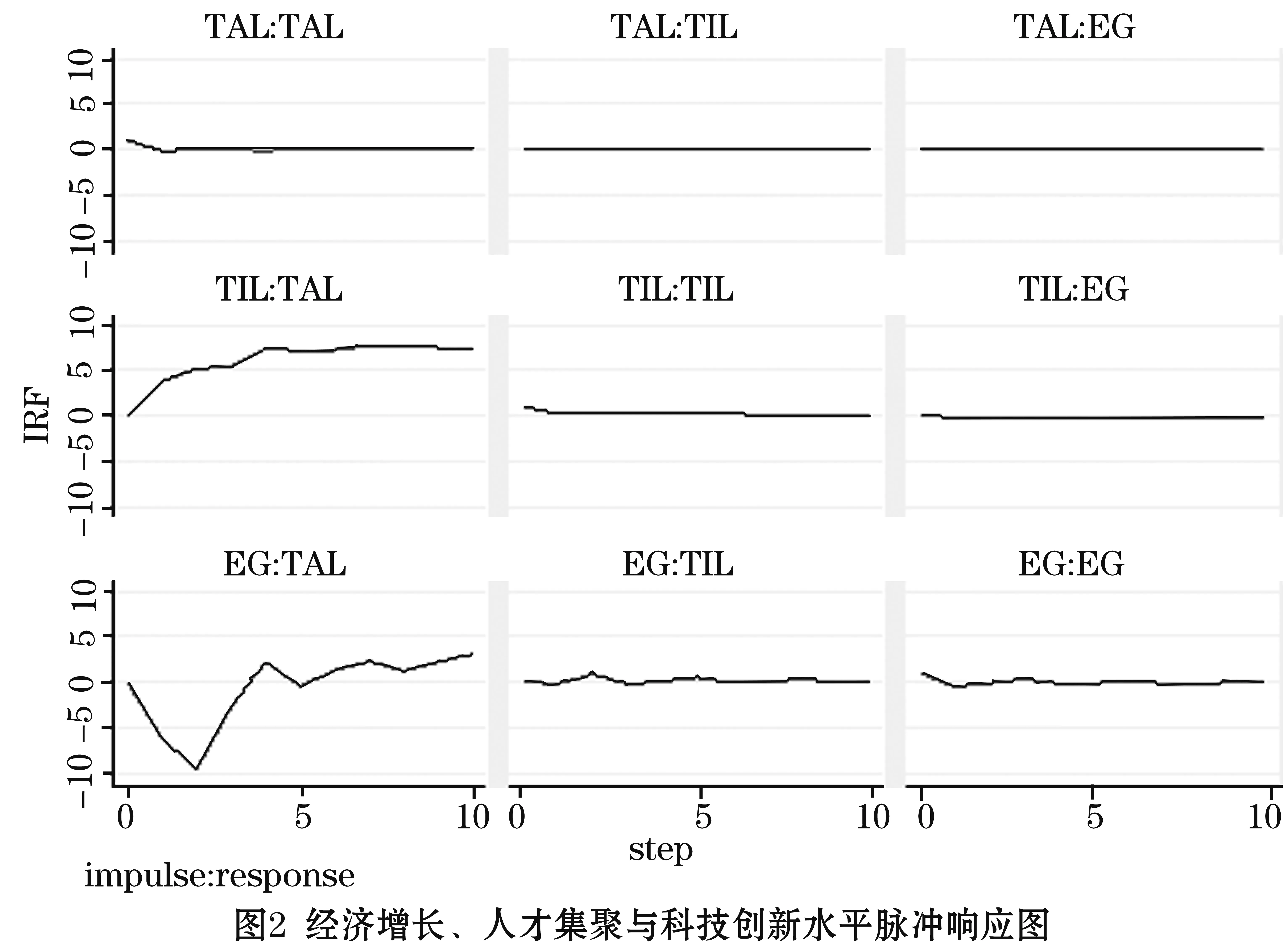
脉冲响应之后，又对三个变量进行方差分解，探究滞后时期各变量所受影响的来源及影响程度，从表5、表6、表7可以看出三个变量的方差分解结果。

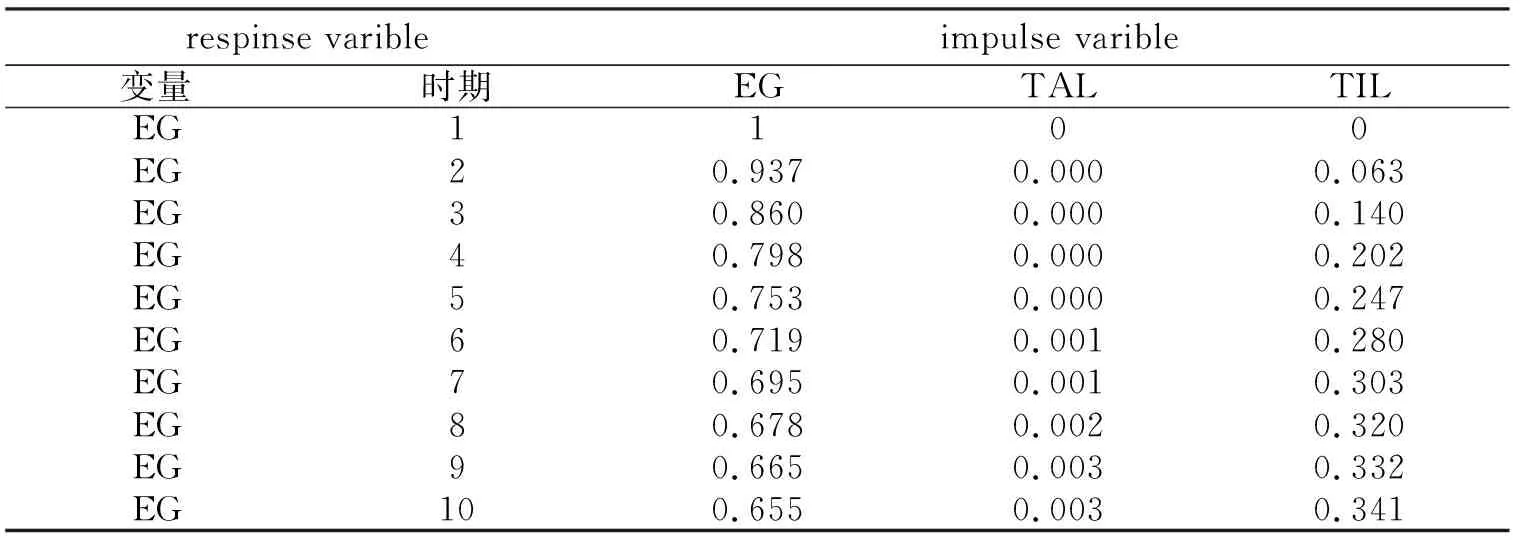
表5 经济增长水平(EG)的方差分解表

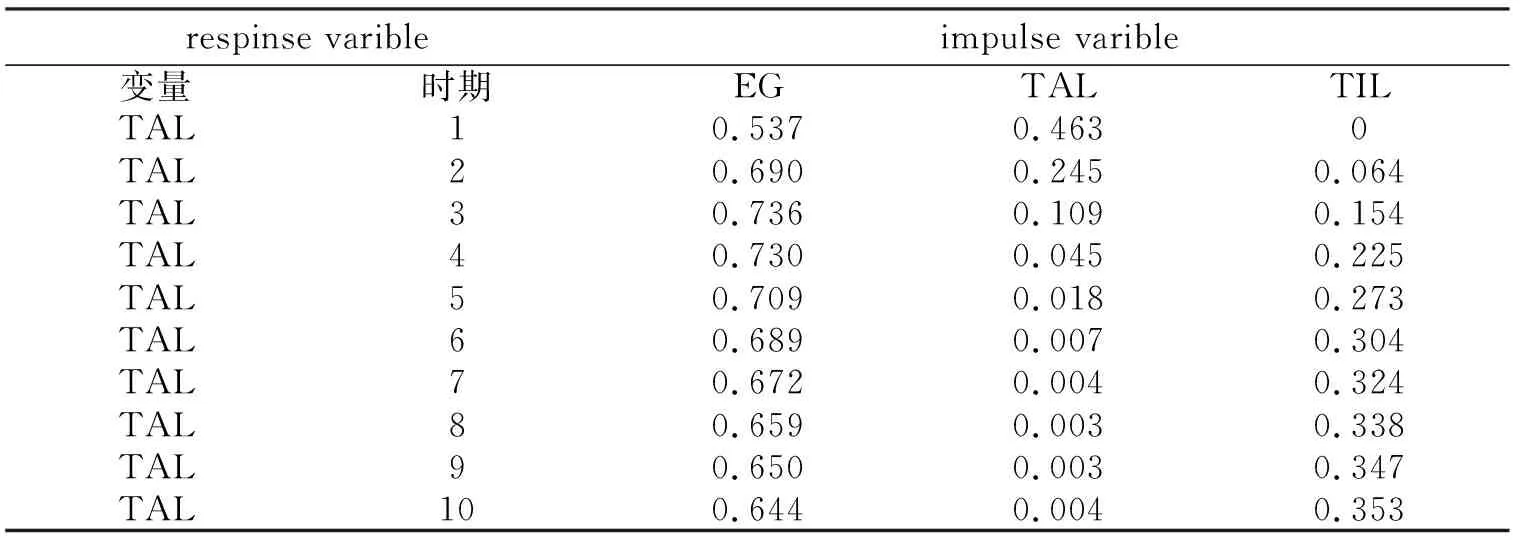
表6 人才集聚水平(TAL)的方差分解表

表7 科技创新水平(TIL)的方差分解表

表5表明，从第1期开始，经济增长水平的变动对自身的变动产生了100%的影响，从第2期开始自身效应占比逐渐减弱。人才集聚的变动对经济增长变动的影响从第1期到第10期是逐渐增长的，第10期的影响达到0.3%。而同期科技创新水平变动对经济增长的影响达到了34.1%，与上文面板数据回归估计结果相同，相比人才集聚，科技创新变动对经济增长变动影响较大。

表6中人才集聚的方差分析结果显示，从第1期开始，影响人才集聚水平变动的因素主要为经济增长及自身变动，相比而言人才集聚对经济增长的变动更为敏感，达到了53.7%，对自身变动影响为46.3%。在接下来的10年，经济增长对人才集聚的影响逐渐增加，到第10年达到了64.4%，科技创新水平的变动对人才集聚水平的变动也产生了越来越大的影响，在第10期达到了35.3%。而人才集聚对自身的影响却逐渐减小，到第10期仅为0.4%。

表7为科技创新的方差分解表，可以看出经济增长及科技创新本身对科技创新的变动影响较大，分别为35%左右和60%左右，并且持续时间较长，10年内也没有显著减小。人才集聚对科技创新的变动虽然相对较弱但也在逐年增强，第10期的影响也达到了4.9%。

五、结论与建议

通过建立PVAR模型，从理论和实证两方面对人才集聚、科技创新以及经济增长之间的交互效应及滞后影响进行了研究。实证研究结果表明，人才集聚及科技创新皆为经济增长的重要动力，人才集聚水平每增加1%，经济增长0.012%；科技创新水平每增加1%，经济增长0.637%。经济增长和科技创新对人才集聚起正向作用，经济增长每增加1%，人才集聚增长2.096%；科技创新每增加1%，人才集聚增长3.187%。经济增长和人才集聚对科技创新起正向作用，经济增长每增加1%，科技创新增长1.098%；人才集聚每增加1%，科技创新增长0.032%。从固定效应模型来看，科技创新对经济增长影响较大，人才集聚对经济增长影响较小，同时经济增长对科技创新的带动作用相对比其对人才集聚的带动作用影响较大。从脉冲响应函数及方差分解结果来看，经济增长及科技创新对人才集聚的正向冲击较为显著，科技创新对经济增长产生的正向冲击大于人才集聚对经济增长产生的正向冲击，且产生的影响持久稳定。因此，政府应加大创新投入，增加科研经费的支出，采取激励手段，提高自主创新能力。在实施人才政策上，要优化人才政策和人才标准，引进高端人才带动优质团队及项目，并提供良好的创业氛围，加大科技创新分配占比，将资源进行合理布局。同时，应加强经济增长(EG)、人才集聚(TAL)及科技创新(TIL)三者之间的良性循环，让三者之间保持相互促进的关系。