差速器轴承摩擦力矩计算模型的构建与验证*
章德平,陈 越,高 勇
(1.武汉轻工大学 机械工程学院,湖北 武汉 430048;2.上汽通用五菱汽车股份有限公司,广西 柳州 545007)
0 引 言
因能源消耗不断增大而导致的全球气候变暖问题,已经引起国际社会的高度关注。为了适应节能减排的国际大环境,汽车行业对汽车产品的燃油经济性提出了越来越高的要求,且相关油耗法规也正在变得越来越严格。对于微型汽车而言,驾驶过程中的燃油消耗主要取决于其自身发动机系统与传动系统的技术状况[1],因此降低工作过程中传动系统的各种功率损耗,提高其传动效率,对于改善微型汽车的燃油经济性具有直接帮助。而轴承作为微型汽车传动系统的关键支承零件,其工作时的摩擦损耗是造成车辆行驶过程中传动系统功率损耗的主要原因,因此其工作性能如何对于微型汽车的燃油经济性具有重要影响[2]。
差速器轴承作为微型汽车驱动桥中的关键零件,主要起着支承用以传递动力的轴和减少动力传递时摩擦损耗的作用。在微型汽车正常行驶时要承受较大冲击,因此需要采取预紧措施。因此,准确预估不同预紧力作用下差速器轴承的摩擦力矩,对于衡量差速器轴承工作时功率损耗具有主要的理论指导意义。
笔者以某型国产微型汽车的差速器轴承为研究对象, 建立了差速器轴承摩擦力矩的数学模型, 并通过实验分别测试了不同预紧状态下的差速器轴承摩擦力矩, 从而验证了该模型的正确性。
1 圆锥滚子轴承摩擦力矩的理论分析
对于一般的圆锥滚子轴承而言,如若处于被施加一定预紧力的状态,其摩擦力矩的产生将主要基于两个方面的原因[3-4]:一是锥形滚动体和轴承内外圈滚道之间因为材料的弹性滞后现象而产生的滚动摩擦,因此所引发的摩擦力矩记为MR;二是锥形滚动体的大端面与轴承内圈挡边之间的滑动摩擦,因此所引发的摩擦力矩记为MS。至于其它原因所造成的滚动轴承摩擦力矩,由于其大小相对于MR和MS而言均较小,因此可以选择忽略不计。
为了使得计算轴承摩擦力矩的过程相对简化,同时考虑到圆锥滚子的锥度较小,因此将圆锥滚子近似简化为圆柱滚子来进行研究,滚动体布置形式保持不变,取简化后滚子轴承的滚道直径为圆锥滚子接触母线中点的轨迹圆直径,而圆柱滚子的直径则取为简化之前的圆锥滚子直径的平均值。对简化滚子轴承某个滚动体开展受力分析,如图1所示,可以得到圆柱滚子关于力与力矩的平衡方程,具体表达式如下:
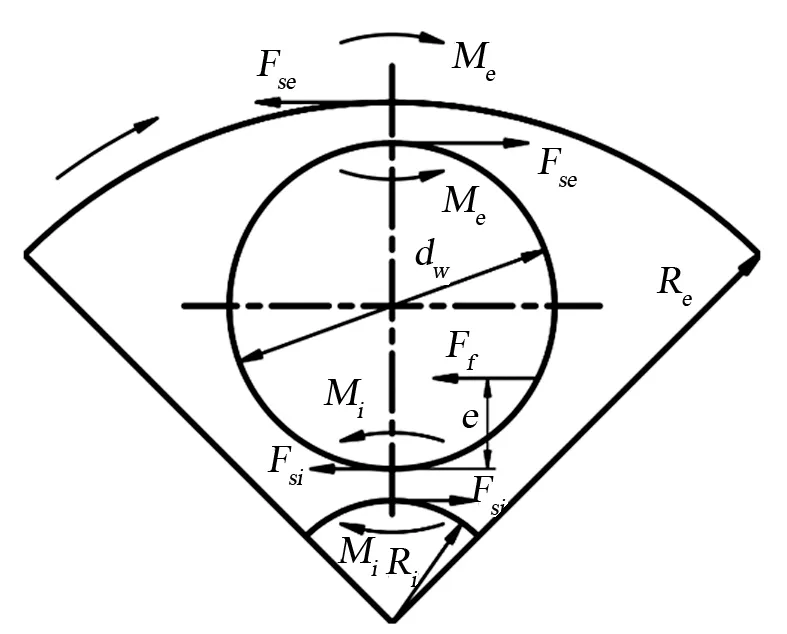
图1 摩擦力矩的产生机理分析
(1)
式中:Fsi为简化的圆柱滚子和内圈沟道之间的滚动摩擦力,N;Fse为简化的圆柱滚子和外圈沟道之间的滚动摩擦力,N;Ff为圆柱滚子端面与内圈挡边之间的摩擦力,N;Mi为简化的圆柱滚子与内圈沟道间的滚动摩擦力矩,N·m;Me为简化滚动体与外圈沟道之间的滚动摩擦力矩,N·m;dw为简化所得圆柱滚子的直径,m;e为内圈挡边和圆柱滚子端面之间的有效接触长度,m。
假定圆柱滚子轴承滚动体的个数为Z,结合滚子轴承摩擦力矩的产生机理,可得以下表达式:
MR+MS=Z(FseRe-Me)
(2)
根据式(1)和(2),可推导得出如下关系式:
(3)
式中:Ri和Re分别为简化后轴承内圈滚道和外圈滚道的半径(单位:m)。
假设圆柱滚子滚动摩擦系数为fk,αe为轴承外圈滚道对滚动体的法向作用力的径向夹角,通过对圆锥滚子轴承单个滚动体进行受力分析,如图2所示,可以发现Fsi、Fse与圆锥滚子轴承所承受的轴向负荷Fa之间具有如下数学关系:
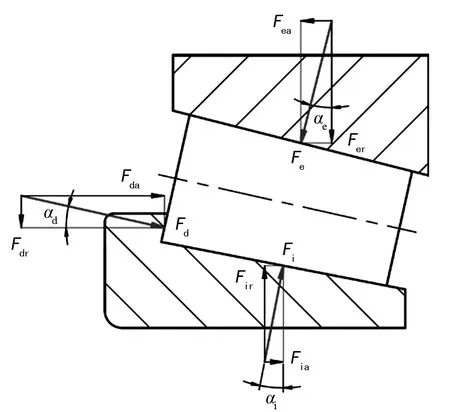
图2 圆锥滚子轴承单个滚动体的受力分析
(4)
假设内圈挡边与滚动体大端面之间的滑动摩擦系数为f,内圈挡边对滚动体大端的法向作用力为Fd,则滑动摩擦力Ff可表示为Ff=fsFd,因此可以得到以下数学表达式:
MR+MS=
(5)
式中:αi和αe分别为内圈滚道、外圈滚道与滚动体之间作用力与轴承径向平面之间的夹角;αd为内圈挡边对滚动体大端的作用力Fd与轴承中心线之间的夹角。
2 微型汽车差速器轴承摩擦力矩的数学模型
就滚动体的结构形式而言,微型汽车差速器轴承与常用圆锥滚子轴承略有不同,主要区别在于微型汽车差速器轴承的滚动体大端面为球形面,而常用圆锥滚子轴承的滚动体端面为平面,滚动体的结构形式如图3所示。就摩擦力矩的组成而言,处于预紧状态下的差速器轴承除了需要考虑滚动体与滚道之间的摩擦以外,还应重点考虑内圈挡边与滚动体大端面之间的摩擦。对微型汽车差速器轴承而言,其滚动体大端面和内圈挡边之间的接触形式为点接触,因此在这里可以考虑使用赫兹理论点接触模型来开展分析。
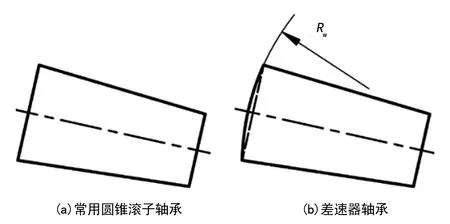
图3 圆锥滚子轴承和差速器轴承滚动体的结构形式
为了研究差速器轴承内圈挡边和滚动体的球基面之间的摩擦机理,文中利用能量理论围绕粘着效应与弹性滞后两个方面进行了深入探讨。
2.1 弹性滞后
弹性滞后产生的主要原因是材料粘弹,这是处于预紧状态的差速器轴承工作时摩擦能量损失的重要原因。如图4所示,在区域D1内任意取一个矩形微元,长度和宽度分别为dx和dy,将坐标系原点取在椭圆接触区域的中心O,假定该微元的坐标为(x,y)。基于赫兹理论的相关结论,点接触的椭圆区域的前半个区域的弹性力相对于区域中心O的矩可描述为:
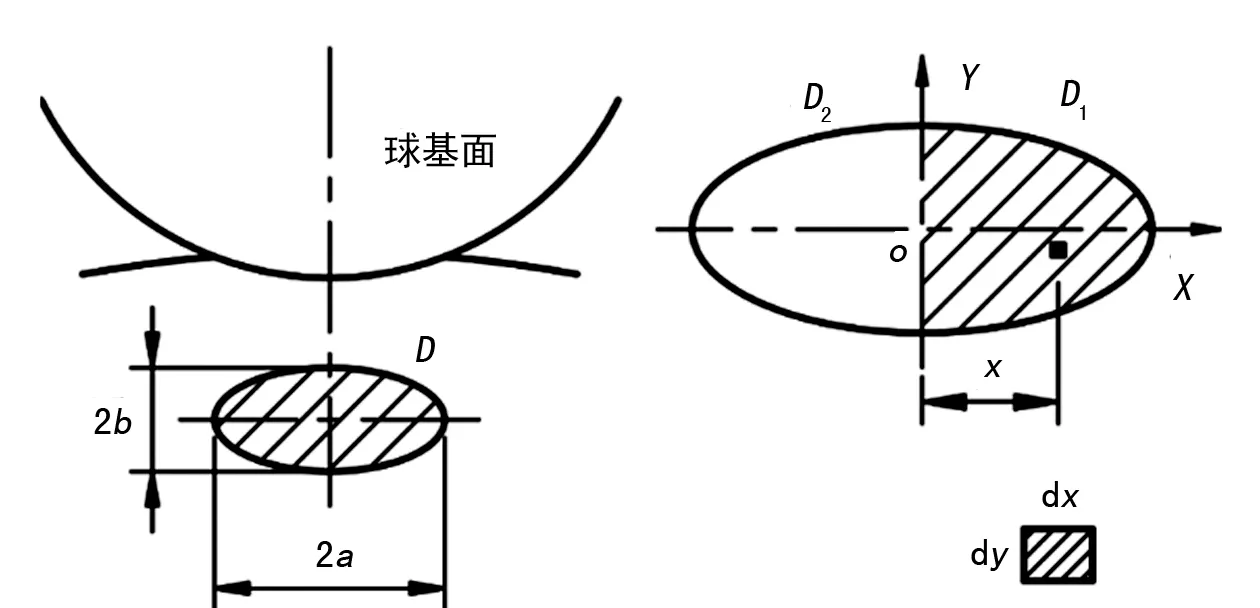
图4 滚子球基面与挡边的接触区域
(6)
式中:a和b分别为椭圆区域的长半轴和短半轴的长度值,mm;p0为接触应力最大值,MPa。
因此,当滚动体运动至与接触区域中心相距为x的位置时,因为弹性滞后而造成的功率损耗为:
(7)
式中:Rw为差速器轴承滚子的球基面半径,mm;ε为滚动体材料与轴承内外圈材料之间的弹性滞后损失系数。
2.2 粘着效应
当承受轴向预紧力的差速器轴承工作时,由于滚动体球基面与内圈挡边接触区域后半部分会因为粘接而受到拉伸作用,从而产生造成能量损失并产生部分滚动阻力。根据文献[6]、[7],应力分布的具体方程式为:
(8)
式中:σs为滚子球基面接触区域中心所对应的最大拉应力,MPa;σb为滚动体与内圈中硬度较低材料的强度极限,MPa。
基于赫兹理论的相关结论,假定实际粘着系数为δT,则点接触的椭圆区域的后半个区域的粘着力相对于区域中心O的矩可描述为:
(9)
当差速器轴承的滚子运动至与接触区域中心相距为x的位置时,因为粘着效应而造成的功率损耗为:
(10)
式中:Q为滚动体和内外圈沟道之间的法向载荷,N;HB为滚动体与内圈中硬度较低材料的接触表面硬度,HB。
因此,根据能量理论可得出滚动摩擦系数f的表达式:
(11)
3 数学模型的仿真分析与实验验证
根据上述已构建的数学模型,利用仿真软件分析差速器轴承的滚子平均直径dw以及滚子数目Z等参数对差速器轴承摩擦力矩的影响规律,仿真结果如图5所示。
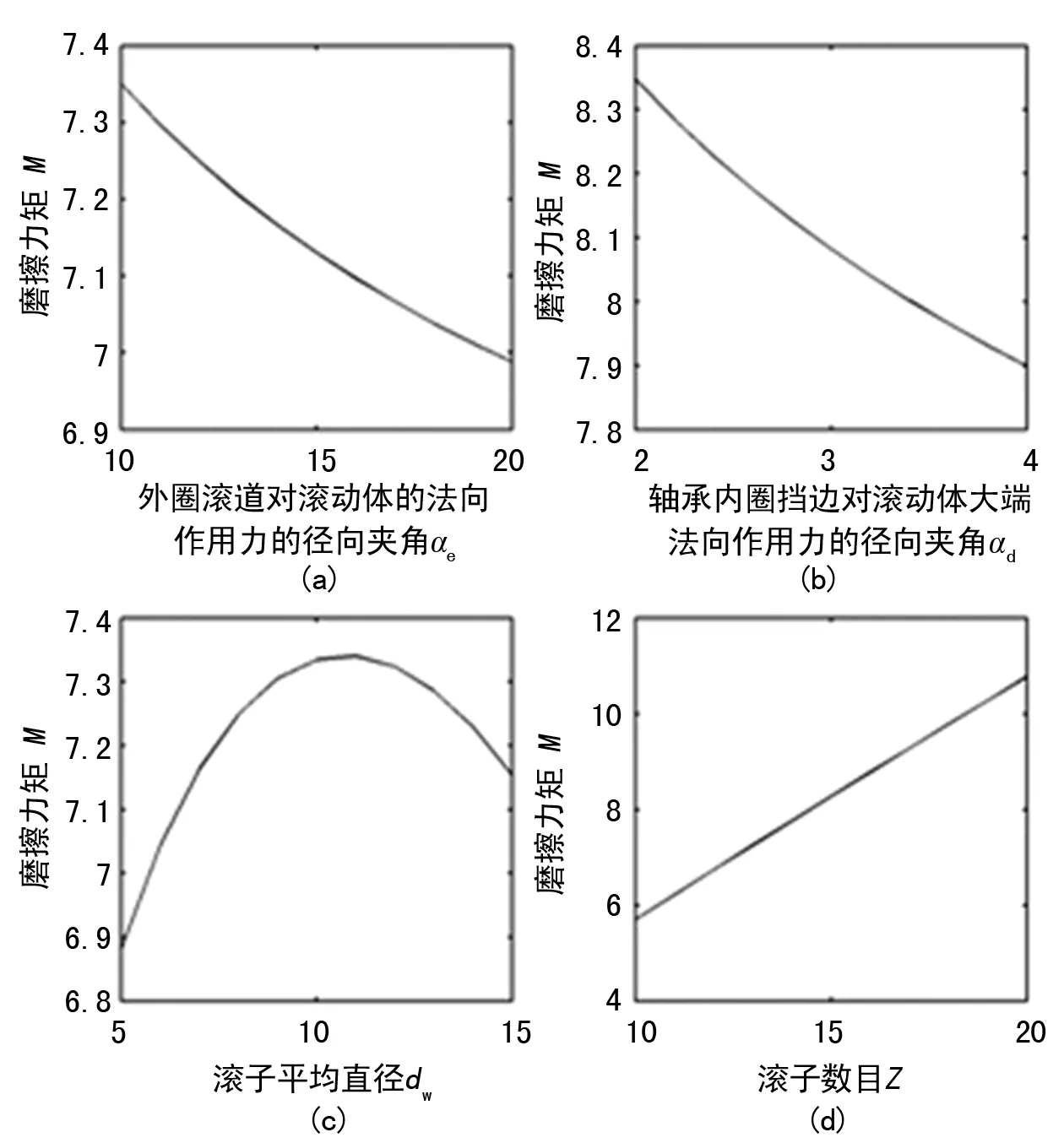
图5 摩擦力矩测试值与理论计算值之间的对比
为了对差速器轴承摩擦力矩数学模型的计算结果进行验证,针对差速器轴承的不同预紧状态,现利用摩擦力矩测量仪对差速器轴承各种状态下的摩擦力矩进行测试。测试时,对差速器轴承沿着轴向施加规定大小的标准力,当差速器轴承平稳低速均匀旋转运动时,可以认为所施加的标准力所产生的标准力矩即为差速器轴承的摩擦力矩[11]。图6为测试原理图。

图6 摩擦力矩测量原理图
使用M9908B摩擦力矩测量仪开展实验测试,并将实验结果与数学模型计算值进行对比,对比结果如图7所示:微型汽车差速器轴承摩擦力矩的测试值与数学模型理论计算值是相当接近的, 大部分误差值均在3% 以下, 而最大误差不超过4.8% , 因此本文中所构建的微型汽车差速器轴承摩擦力矩的数学模型能够较为准确地描述处于预紧状态下的差速器轴承的摩擦力矩。
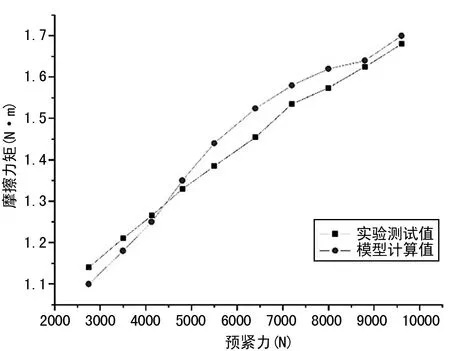
图7 摩擦力矩测试值与理论计算值之间的对比
进一步观察数学模型理论计算值可知, 对于处于预紧状态下的微型汽车差速器轴承而言, 其摩擦力矩的大小与轴承自身所承受的轴向负荷正相关,近似满足直线关系。
4 结 论
通过理论推导,构建了微型汽车差速器轴承摩擦力矩的数学模型,并利用实验测试验证了模型的正确性。主要结论如下:
(1)对于微型汽车差速器轴承而言,由于其滚动体的大端面是球形端面,因此其摩擦力矩的数学计算模型与常用圆锥滚子轴承滚动体相比有所不同,总体偏小。
(2)对于处于预紧状态下的差速器轴承而言,其摩擦力矩的大小与轴承所承受的轴向负荷Fa有直接关系。
(3)通过开展实验测试,将得到的测试结果与所构建的数学模型的理论计算值进行比较,发现两者之间具有较好一致性,最大误差不超过4.8%,从而验证了模型的可靠性。

