一类具有负交叉扩散的SIS 传染病模型的Turing 稳定性

陈清婉，柳文清

（闽南科技学院 通识教育学院，福建 泉州362300）

当前新冠肺炎病毒在全球大面积传播，深入研究传染病的传播机制，具有非常重要的现实意义。许多学者利用动力学原理建立了多种传染病数学模型，并取得了很好的研究成果[1-5]。近来，一类总人口满足Logistic 增长以及受心理作用影响的SIS 传染病模型受到关注[6-9]，文[6]建立了一类SIR 传染病模型如下

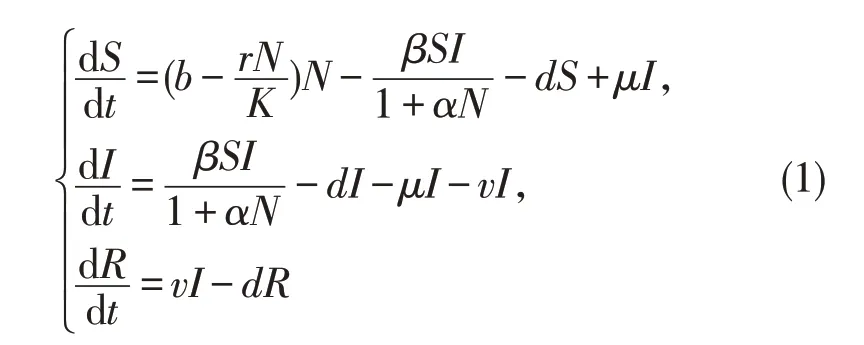
其中：S,I,R 分别是t 时刻易感者，染病者和恢复者的数量，N=S+I+R 为总人口数，b 表示自然增长率，d 表示自然死亡率，r=b-d 为内禀增长率，K 表示环境容纳量；μ 表示恢复率和治愈率的和；v 为获得的终身免疫率；β 表示潜伏者和染病者的有效接触率；参数α(0 ＜α ＜1)表示心理作用系数，即传染病发生时人们采取了相应的预防措施，从而影响疾病的发生。

文[7]则研究了一类SIS 传染病模型

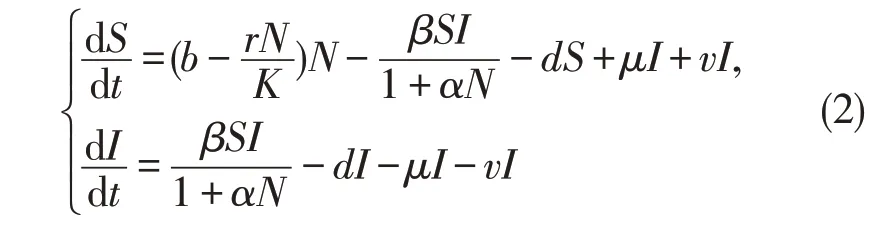
其中：(x,t)∈Ω×(0,T)；d11,d22＞0 表示自扩散系数，它是由空间分布不均匀引起的扩散，d12＞0,d21＞0表示交叉扩散系数。传染病模型带正的交叉扩散系数，表示人群总是从另一人群的高密度区域向低密度区域移动，表现为染病者远离易感者的现象；而传染病模型带负的交叉扩散系数，表示人群从低密度区域向高密度区域移动，表现为染病者向易感者移动的现象。更多的交错扩散模型的研究可参看文献[10-15]。

容易得到，模型(3)与模型(2)有相同的常数平衡点，将模型(2)中的两个方程相加可得

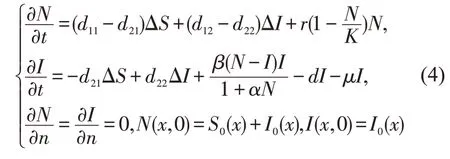
本文将讨论由负交叉扩散系数引起的Turing失稳。在阈值R0≤1 条件下，负交叉扩散系数较小时，无病平衡点局部渐近稳定，负交叉扩散系数较大时，无病平衡点不稳定；阈值R0≥1 条件下，负交叉扩散系数较小时，染病平衡点局部渐近稳定，负交叉扩散系数较大时，染病平衡点不稳定。

1 负交叉扩散引起的Turing 失稳

记Ω 上的算子Δ 在齐次Neuuman 边界条件下的特征值序列为0=μ0≤μ1≤…≤μk≤…，将模型(3)中方程改写为如下形式

此时特征方程有一正特征根，染病平衡点E*=(S*,I*)不稳定。

2 数值模拟

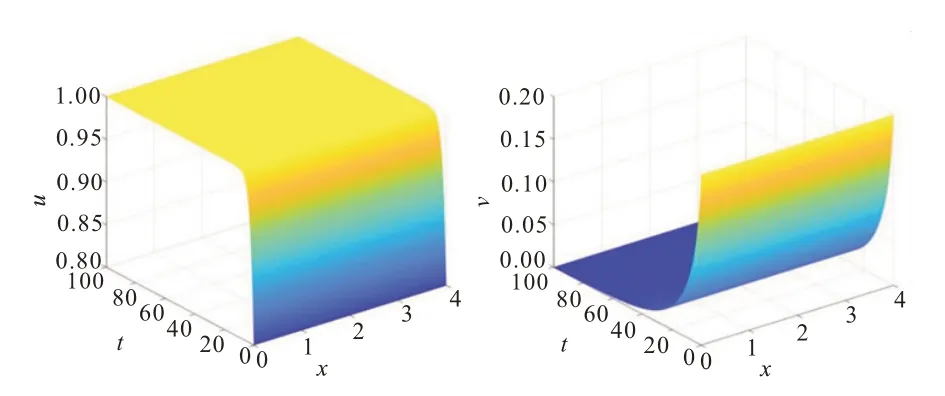
图1 d21=0.1时平衡点E0=(1,0)局部渐近稳定

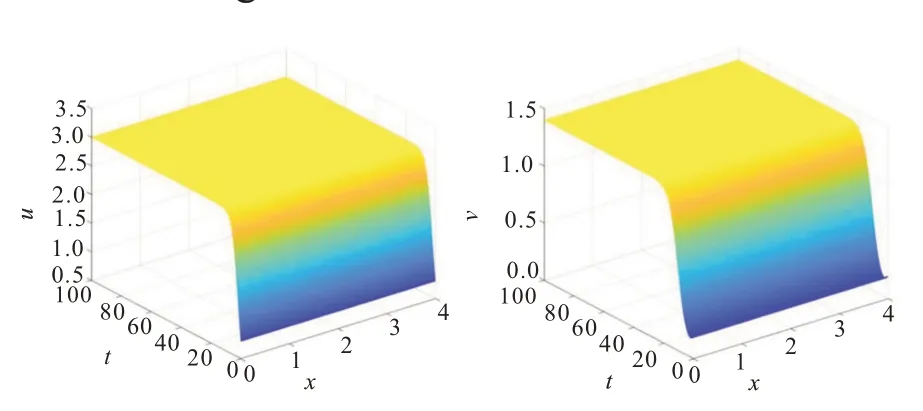
图2 取d21 ≤0.6 时，衡点E*局部渐近稳定

3 小结

由上述定理结论可知，对于交叉扩散传染病模型，阈值不再是疾病流行与否的唯一衡量指标，负交叉扩散的传染病模型,染病者向易感者移动的速度会影响着传染病的传播。当负交叉扩散系数d21较小时，平衡点局部渐近稳定，当负交叉扩散系数d21较大时，平衡点失稳。