准星象函数的若干系数估计

何良苗，王麒翰，龙波涌

（安徽大学 数学科学学院，安徽 合肥230601）

准星象函数有许多有趣的几何性质。当参数α=1 时，准星象函数是将单位圆满射到一个凸域的凸函数。当参数α=1/2 时，准星象函数又是阶为1/2 的星象函数。目前，数学工作者只研究了准星象函数的部分性质。例如，准星象函数的包含关系，广义的准星象函数，以及准星象函数复合一个莫比乌斯变换后仍然是准星象函数等。有关准星象函数的系数估计也备受关注。

1 预备知识

设H(Ω)表示在区域Ω 内的解析函数全体。记H1(Ω)={zf ∶f ∈H0(Ω)} 其 中H0(Ω)={f:f(0)=1,且f ∈H(Ω)}，则H1(Ω)中的函数有表达式

设f ∈H1。 f 为a 阶星象函数与a 阶凸函数当且仅当

其中n,q ∈N。

本文首先建立了关于函数类P 系数的一个最佳估计式。再通过建立起Ra与P 相互之间的系数关系，分别估计了Ra的Hankel 行列式H2(2)和H2(3)的上界，以及Fekete-Szegö 泛函和Zalcman泛函的上界，得到了相应的结果。其中Fekete-Szeg ö泛函上界的估计是最佳。

2 主要结果

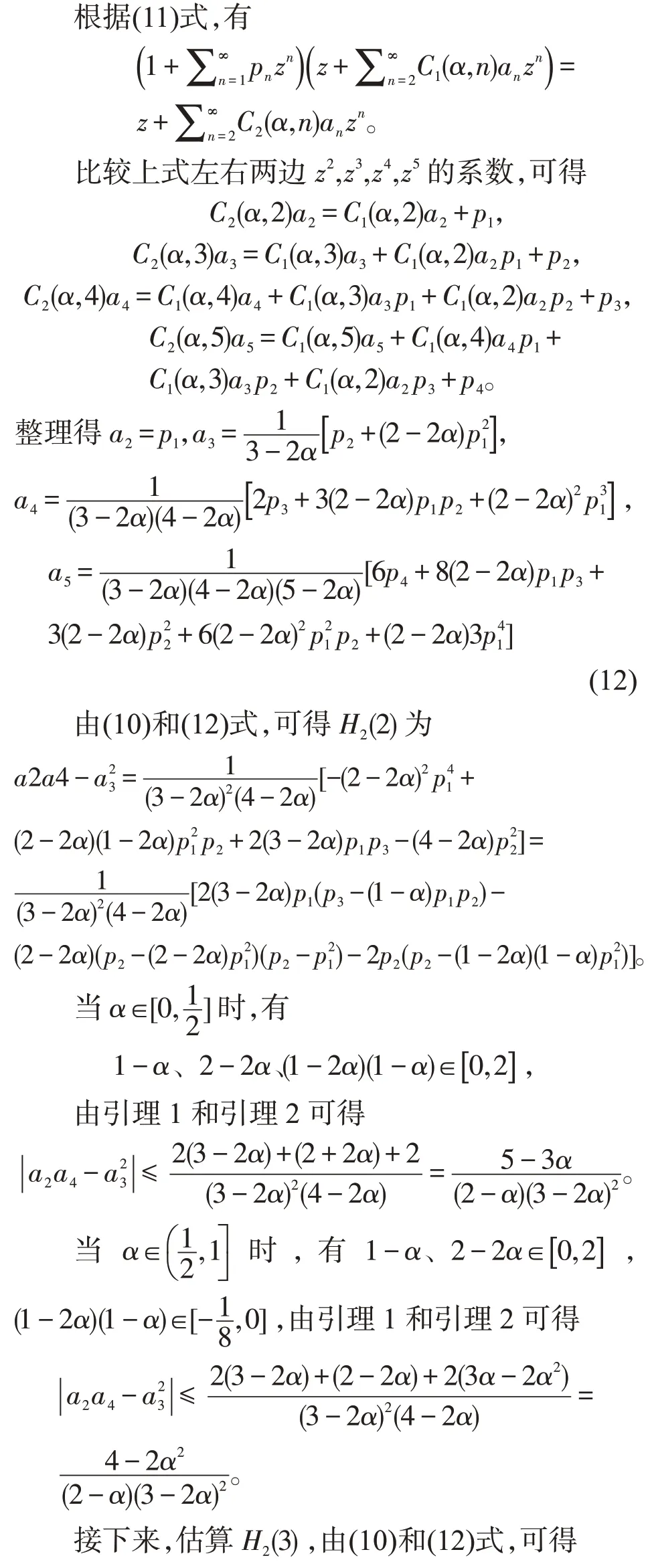
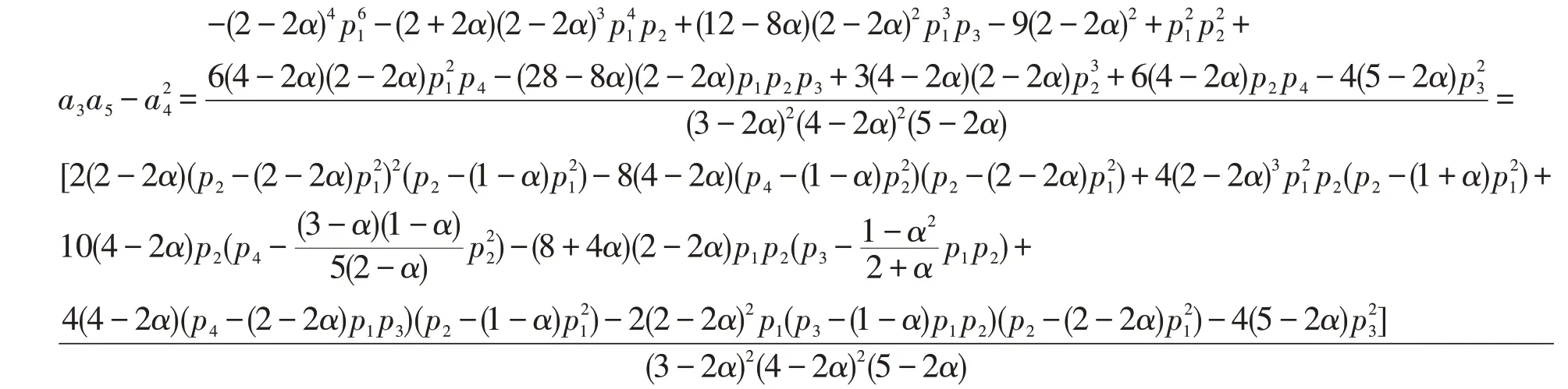
从而定理得证。

根据(3)式，不难发现，当α=1/2 时，R1/2=S1/2；当α=0 时，R0=C0。

3 小结

首先建立了关于函数类P 系数的一个最佳估计式。再建立起Ra与P 相互之间的系数关系，分别估计了Ra的Hankel 行列式H2（2）和H2（3）的上界，以及Fekete-Szegö 泛函和Zalcman 泛函的上界，得到了相应的结果。其中Fekete-Szegö 泛函上界的估计是最佳。