t-blocking集合的一个新上界*
曹金明, 种文文
(湖南大学 数学与计量经济学院,湖南 长沙 410082)
t-blocking集合的一个新上界*
曹金明*, 种文文
(湖南大学 数学与计量经济学院,湖南 长沙 410082)
给出了PG(2,q)上的t-blocking集合的一个一般上界,此上界比以往的上界稍好,同时对知之甚少包含一条线的t-blocking也给出了一个上界.
二维有限射影空间PG(2,q);t-blocking集合;上界



1)k≥(2t+1)(p+1)/2,q=p为素数且p>3,t
2)k≥(t+1)pq=p为素数,且p>3,t≥p/2(见文献[1]);

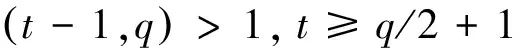
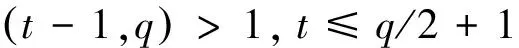

下面,我们将给出t-blocking 集合的一个新上界.
1 关于不包含一条线的t-blocking集合的一个新上界

下面,我们将给出Ball定理的一个初等证明,并对结果进行改进,得到k的一个更大的下界.改进的结果如下:
定理1.2 设K为PG(2,q)中一个有k个元的t-blocking集,若K不包含一条直线,则
当1 下面给出一些符号和一些能够证明其成立的等式的说明. 归纳以上的结论.得到如下等式: (2) 现在证明q>3的情况. 解这个不等式: 定理2.1 设K是PG(2,q)的一个t-blocking 集合,如果K包含一条直线,则 证明 下面我们分两种情况讨论: =(x+mq)(x+mq-1)-(x+m-1)(x+mq)(q+1)+xmq(q-1)≤0. [1] BALL S.Multiple blocking sets and arcs in finite planes[J].J London Math Soc,1996,54:581-593. [2] BLOCKHUIS A.On multiple nuclei and a conjecture of Lunell[J].Soc Ball Bull Belg Math Soc,1994,3:349-353. [3] BRUEN A A.Blocking sets in finite projective planes[J].SIAM J Appl Math,1971,21:380-392. [4] BRUEN A A,THAS J A.Blocking sets[J].Geom Dedicata,1977,6:193-203. [5] BALL S.Multiple blocking sets and arcs[J].Finite Fields Appl,1996,2:125-137. [6] BRUEN A A.Polynomial multiplicities over finite and intersection sets[J].J Combin Theory,1992,60(A):19-33. 责任编辑:龙顺潮 A New Upper Bound oft- Blocking Collection CAOJin-ming*,ZHONGWen-wen (College of Mathematics and Econometrics University, Changsha ,Hunan 410082 China) A general upper bound oft-blocking is given in this paper, and the upper bound is slightly better than the upper bound of the previous,t-blocking while little is known contain a line also gives an upper bound. two-dimensional finite projective space;t-blocking set; upper bound 2015-01-10 国家自然科学基金项目(11271116) 曹金明(1961— ),男,湖南 长沙人.教授.E-mail:1446477152@qq.com O A 1000-5900(2015)01-0001-03








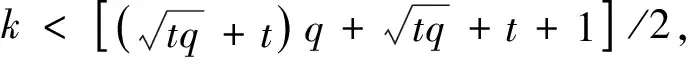


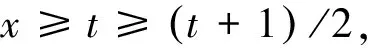
2 关于包含一条线的t-blocking集合的一个上界

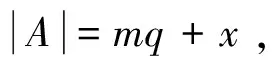
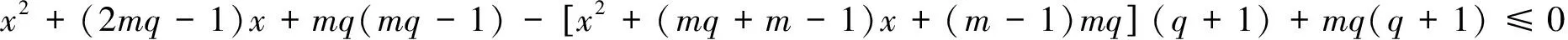
——《计量经济学方法论研究》评介

