正交各向异性功能梯度材料周期裂纹问题研究*

丁生虎, 李 星, 杨 娟,2

(1.宁夏大学 数学计算机学院,宁夏 银川 750021; 2.宁夏大学 民族预科教育学院,宁夏 银川 750002)

正交各向异性功能梯度材料周期裂纹问题研究*

丁生虎1*, 李 星1, 杨 娟1,2

(1.宁夏大学 数学计算机学院,宁夏 银川 750021; 2.宁夏大学 民族预科教育学院,宁夏 银川 750002)

研究了正交各向异性功能梯度材料含平行周期裂纹的平面 I 型和 II 型断裂问题. 考虑正交各向异性的主轴方向分别为平行和垂直于带的边界, 运用 Fourier 变换, 将混合边值问题的求解转化为求解第一类 Cauchy 奇异积分方程, 获得了周期裂纹尖端应力场. 结果显示了非均匀材料参数, 材料力学性质和裂纹间距对应力强度因子的影响，对功能梯度材料的设计及应用有参考价值.

正交各向异性；功能梯度材料；周期裂纹；奇异积分方程

功能梯度材料(FGMs)设计的显著特点是通过调整材料组分的变化规律, 最大限度地降低热/残余应力对其性能的影响[1]. 功能梯度材料断裂力学研究对于功能梯度材料的设计、制造及应用具有十分重要的指导意义. 戴耀等[2]从裂纹尖端渐近场、应力强度因子、 断裂失效准则和动态断裂问题等方面阐述了功能梯度材料弹性断裂分析的研究方法、进展和主要结论. 目前已经有很多学者对功能梯度材料断裂力学进行了研究[3～9]. 由于数学处理上的困难, 目前大多数有关功能梯度材料裂纹问题的理论分析均假设材料为各向同性弹性体, 但实际制备工艺的特点决定了功能梯度材料将很少是各向同性的. 由于问题的复杂性, 研究各向异性功能梯度材料断裂行为的文献不多. Ozturk 和 Erdogan[10]研究了无限大正交各向异性功能梯度材料受静态机械载荷作用下的裂纹方向平行于材料属性梯度方向的 I 型断裂问题. 李春雨等[11]采用积分变换-对偶积分方程方法, 研究了正交各向异性功能梯度材料反平面裂纹问题. 假设裂纹方向和材料的梯度方向平行, Guo 等[12]研究了正交各向异性功能梯度条的内嵌裂纹和边裂纹问题. Chen 等[13]假设材料的物性参数按指数形式变化, 研究了含平行于边界的有限厚度正交各向异性功能梯度板条的稳态温度场问题. Ding 和 Li[14]研究了一正交各向异性功能梯涂层粘结到一均匀基底含共线裂纹的平面 I 型断裂问题.

以上研究的都是单裂纹和共线裂纹, Dag等[15]用解析和数值方法分别研究了非均匀正交各向异性功能梯度材料界面裂纹和周期界面裂纹问题. 本文研究了正交各向异性功能梯度材料的周期裂纹问题, 采用积分变换技术, 所求的问题转化为第一类 Cauchy 奇异积分方程, 获得了周期裂纹尖端应力场. 所获得的结果对工程结构裂纹止裂具有理论意义和实用价值.

1 问题的提法

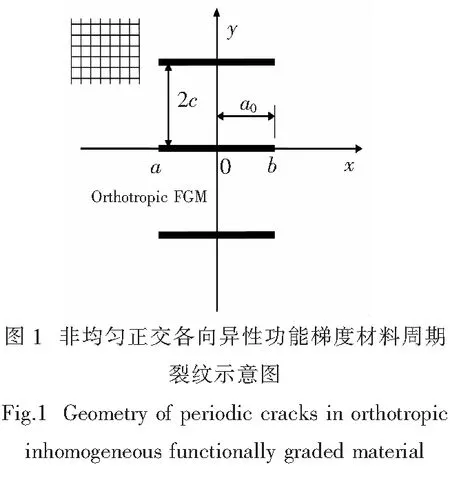
如图 1 所示, 一正交各向异性功能梯度材料里有长度为 2a0的一列平行于x轴的周期裂纹, 周期为 2c,x和y坐标轴为正交主轴. 假设正交各向异性介质的梯度方向沿着x轴变化

(1)

其中β是正或负的非均匀参数.

对图 1 中的混合边值问题, 受I型载荷的边界和连续性条件为

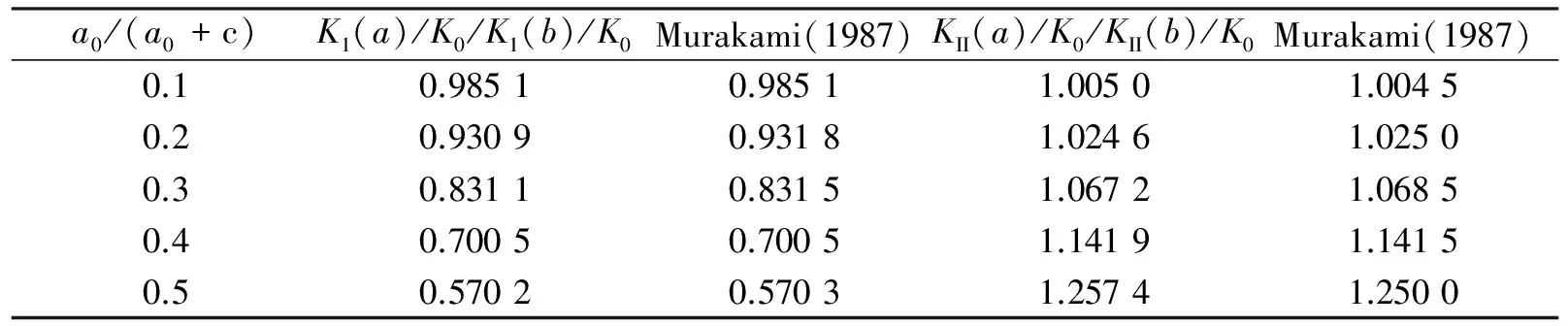
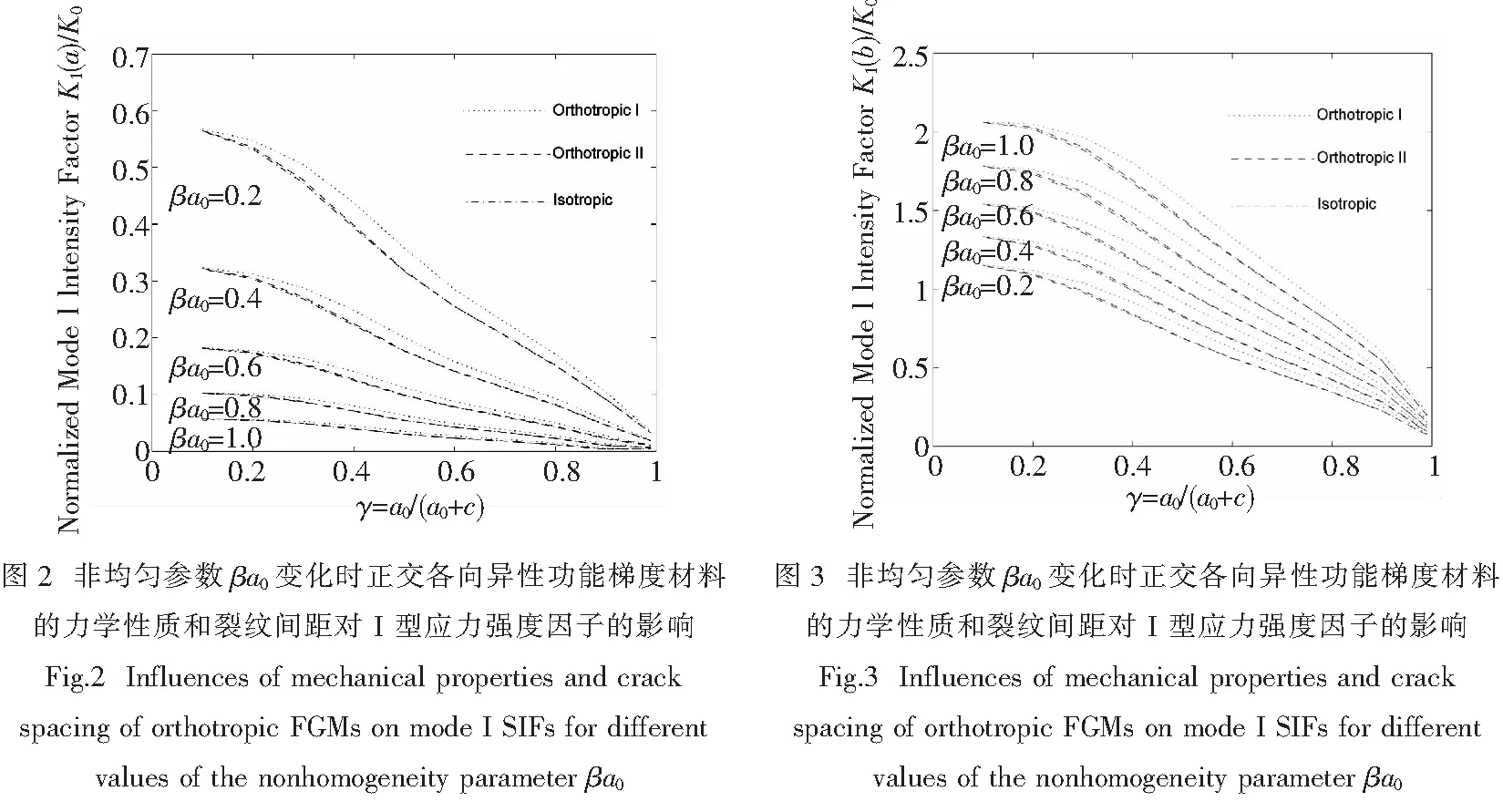
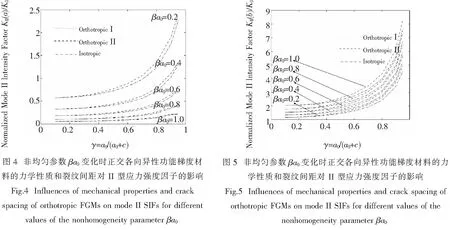
σyy(x,0)=δ(x),a

(2)

v(x,0)=0,xb,

(3)

τxy(x,0)=0,τxy(x,c)=0, -∞

(4)

v(x,c)=0, -∞

(5)

受II型载荷的边界和连续性条件为

τxy(x,0)=τ(x),a

(6)

u(x,0)=0,xb,

(7)

σyy(x,0)=0,σyy(x,c)=0, -∞

(8)

u(x,c)=0, -∞

(9)

2 问题求解

由于结构对称, 我们只考虑上半平面, 运用 Fourier 变换, 位移可以表示为

(10)

这里Aj(s) 是未知函数,mj和Bj(s) 是已知函数.

我们引入两个新的函数

(11)

由边界条件 (2)～(9), 经过推导, 有

(12)

其中

Hj(r,u)=Hj(x,t)(b-a)/2,gj(u)=gj(x),δ(r)=δ(x)e-βx,τ(r)=τ(x)e-βx,

(13)

这里Hj(j=1,2)为已知函数.

方程 (12) 的解可以表示为[16]

(14)

这里G1(u) 和G2(u) 为有界函数,依据Chebyshev正交多项式将它们展开为

(15)

其中Tn是Chebyshev第一类多项式,An,Bn是未知常数.

An和Bn可以通过求解线性方程组得到, 裂纹的应力强度因子 (SIFs) 定义为

(16)

(17)

(18)

(19)

3 数值算例和分析

表1 正交各向异性功能梯度材料的力学性质

表2 均匀材料裂纹间距对正则化 I, II 型应力强度因子的影响

图2和3给出了非均匀参数βa0变化时正交各向异性功能梯度材料的力学性质和裂纹间距对I型应力强度因子的影响. 结果表明三种材料中材料III即各向同性材料给出的应力强度因子最小, 裂纹尖端x=a处应力强度因子随着非均匀参数βa0的增加而减小, 裂纹尖端x=b处应力集中表现得更强烈, 并随着非均匀参数βa0的增加而变大. 随着裂纹间距的变大，非均匀参数βa0对应力强度因子的影响逐渐变得显著；当裂纹间距逐渐变小时，裂纹之间的相互影响导致了应力强度因子的大幅减小，这种趋势在非均匀参数βa0=1.0时最为明显. 在工程中适当控制非均匀参数的变化有利于提高材料的抗断裂能力.

图4和5给出了非均匀参数βa0变化时正交各向异性功能梯度材料的力学性质对II型应力强度因子的影响. 结果表明三种材料中材料III即各向同性材料给出的应力强度因子最小, 裂纹尖端x=a处应力强度因子随着非均匀参数βa0的增加而减小, 裂纹尖端x=b处应力强度因子随着非均匀参数βa0的增加而变大. 非均匀参数βa0对应力强度因子的影响随着裂纹间距的减小而变得逐渐明显，当裂纹间距逐渐变小时，不管非均匀参数βa0如何变化，裂纹之间的相互影响导致了此时应力强度因子的值超过了相同长度单裂纹的应力强度因子的值. 工程中裂纹间距和非均匀参数的变化可降低或增加裂纹尖端应力集中的程度, 可通过参数控制预报因裂纹扩展造成的工件失效问题.

4 结 论

研究了正交各向异性功能梯度材料的周期裂纹问题, 采用积分变换技术, 所求的问题转化为第一类 Cauchy 奇异积分方程, 获得了周期裂纹尖端应力场. 结果表明: 对三种材料而言, 材料 III 即各向同性材料给出的应力强度因子最小. 对于 I 型应力强度因子, 当裂纹间距变大时，非均匀参数βa0对应力强度因子的影响逐渐变得显著.II型应力强度因子有着I型应力强度因子类似的性质, 但是非均匀参数βa0对应力强度因子的影响随着裂纹间距的减小而变得逐渐明显. 从研究结果来看, 在材料较硬侧的裂纹相对比在另一侧更不稳定.

[1] 凌云汉，白新德，李江涛，等. W/Cu 功能梯度材料的热应力优化设计[J].稀有金属材料与工程，2003, 12：976-980.

[2] 戴耀，燕秀发，陈敏文，等. 功能梯度材料的弹性断裂分析[J].稀有金属材料与工程，2005, 8：1 191-1 195.

[3] 黄干云, 汪越胜, 余寿文. 功能梯度材料的平面断裂力学分析[J].力学学报，2005, 37：1-8.

[4] 李永东, 张洪才, 贾斌,等. 功能梯度双材料弱/微间断界面的冲击断裂分析[J].力学学报，2006, 38：559-564.

[5] LU C F, CHEN W Q, ZHONG Z. Two-dimensional thermoelasticity solution for functionally graded thick beams[J].Science in China Series G-Physics, Mechanics & Astronomy，2006, 49：451-460.

[6] 程站起, 仲政. 功能梯度材料涂层平面裂纹分析[J].力学学报,2007, 39：685-691.

[7] LI X F, FAN T Y. Dynamic analysis of a crack in a functionally graded material sandwiched between two elastic layers under anti-plane loading[J].Composite Structures, 2007(2):211-219.

[8] DING S H,LI X. Mode-I crack problem for functionally graded layered structures[J].International Journal of Fracture, 2011, 2:209-226.

[9] 孔艳平, 刘金喜. 功能梯度压电双材料板中厚度-扭曲波的传播[J].工程力学, 2012(7):24-29.

[10] OZTURK M, ERDOGAN F. Mode I crack problem in an inhomogeneous orthotropic medium[J].International Journal of Engineering and Science,1997, 35:869-883.

[11] 李春雨, 邹振祝, 段祝平. 正交各向异性功能梯度材料反平面裂纹尖端应力场[J].固体力学学报,2001(1):81-84.

[12] GUO L C, WU L Z, ZENG T. The dynamic response of an edge crack in a functionally graded orthotropic strip[J].Mechanics Research Communications,2005, 32:385-400.

[13] CHEN J, SOH A K, LIU J X,et al. Thermal fracture analysis of a functionally graded orthotropic strip with a crack[J].International Journal of Mechanics and Materials,2004(1)：131-141.

[14] 丁生虎,李星,黄凌霄,等. 正交各向异性功能梯度涂层-基底结构共线裂纹问题的断裂分析[J].固体力学学报,2011(6):109-113.

[15] DAG S, YILDIRIM B, ERDOGAN F. Interface crack problems in graded orthotropic medium: analytical and computational approaches[J].International Journal of Fracture,2004, 130:471-496.

[16] COOK T S, ERDOGAN F. Stresses in bonded material with a crack perpendicular to the interfaces[J].International Journal of Engineering Science,1972, 10:677-697.

[17] MURAKAMI Y. Stress intensity factors handbook[M].New York:Pergamon Press ,1987.

责任编辑：罗 联

Research of Periodic Cracks Problem for Functionally Graded Orthotropic Material

DINGSheng-hu1*,LIXing1,YANGJuan1，2

(1.School of Mathematics and Computer Science, Ningxia University, Yinchuan 750021;2.Institute of Ethnic Preparatory Education, Ningxia University, Yinchuan 750002 China)

This paper investigates the mode I and mode II crack problem of a periodic array of parallel cracks in a functionally graded orthotropic material. The principal axes of orthotropy are assumed to be parallel and perpendicular to the crack plane. By using Fourier transforms, the mixed boundary value problem was reduced as a system of Cauchy singular integral equations of the first kind. The local stress field around the periodic cracks tip was obtained. The influences of parameters such as nonhomogeneous parameter, the material mechanics properties and crack spacing on the stress intensity factors (SIFs) are studied. The results obtained have the reference value in the design and application of functionally graded materials.

orthotropic；functionally graded materials； periodic cracks； singular integral equations

2014-12-04

国家自然科学基金项目(11362018,11261045,11202112)

丁生虎(1980— ),男，宁夏 同心县人,博士，副教授.E-mail:dshsjtu2009@163.com

O346

A

1000-5900(2015)01-0004-05