暗挖装配式区间管片接缝密封垫老化研究

董林伟，杨志勇，江玉生，王振勇，王号，孙子越，齐明玉

中国矿业大学(北京)力学与建筑工程学院，北京 100083

截至2019年底，我国有40个城市开通了城市轨道交通的运营，运营总里程达6 730 km[1]。随着城市轨道交通向更深发展，隧道工程的渗漏水问题越来越突出，工程技术人员对隧道防水越来越重视。密封垫作为防水材料，1969年首次应用于德国汉堡的易北河水下公路隧道中[2]。隧道的设计使用年限是100年，在设计时不仅要满足短期阻挡外界水压的要求，还要保证其具有一定的耐久性，能够满足隧道长期防水的要求。目前，隧道管片的接缝防水主要依靠密封垫[3-5]，尤其对于地下水位较高的隧道而言，接缝密封垫的设计直接影响着隧道的使用[6-9]。

管片接头采用三元乙丙橡胶密封垫作为接缝防水材料。导致橡胶材料老化的因素主要有温度、气体、化学物质(酸、碱)、生物(微生物、昆虫)等环境因素。橡胶材料在老化过程中性能会逐渐劣化，造成密封垫压力减小、抗渗能力降低，最终导致管片接头部位发生渗漏水[10-12]。针对密封垫的老化，很多学者进行了研究。Tan等[13]对遇水膨胀橡胶和遇水膨胀聚氨酯密封垫的长期遇水膨胀性能进行了研究。伍振志[14]和丁杨等[15]研究了管片密封垫老化对应力松弛的影响。张家奇等[16]对在老化条件下密封垫延伸率和拉伸弹性模量的变化规律进行研究。张子新等[17]进一步考虑了密封垫沟槽对密封垫老化的影响。

在密封垫老化试验中，主要考核拉断伸长率、压缩永久变形量等几个指标。鉴于接缝密封垫在防水条件下处于受压状态，本文采用压缩永久变形量作为衡量其耐久性的指标[18]。基于加速老化试验数据，通过测定密封垫的压缩永久变形量，建立三元乙丙橡胶密封垫的性能变化函数，预测其在正常工作条件下的使用寿命，并通过编制的计算程序，解决了老化试验数据处理中经验常数的试算问题，可有效降低数据处理的难度。此外，为研究老化对密封垫防水性能的影响，开展了针对密封垫接触应力的数值模拟研究。

1 工程背景

本文以北京地铁6号线起点—金安桥暗挖区间管片接缝所用的密封垫作为研究对象。该隧道首次采用了暗挖+装配式二衬的结构形式。装配式二衬借鉴了盾构的装配形式，每环由六种不同形式的管片组成，管片布置如图1所示。该工法与盾构法区别在于：在采用矿山法开挖隧道断面并采取初期支护措施后，依靠特制的拼装机进行管片的拼装。该工法适应性强且自动化程度高，可克服盾构法在一些特殊的复合地层(上软下硬的第四系土层、岩石地层、岩土复合地层以及含有球状风化体的地层)中施工困难的缺点。此外，马蹄形隧道也提高了开挖断面利用率。

图1 管片截面形式

该段区间底板埋深22.22～29.18 m。拟建线路区间地层分别为人工堆积层、新近沉积层和第四纪晚更新世冲洪积层以及三叠系双全组基岩。第四系沉积物以古金沟河故道沉积为主。装配式区间的地质剖面如图2所示。

图2 装配式区间地质剖面

2 橡胶材料老化模型

研究表明，影响橡胶材料老化的最主要因素为温度、氧气、紫外线[19]。管片接缝密封垫应用于地下环境，主要考虑温度和氧气对密封垫老化的作用[20-21]。

根据时温等效原理[22-23]，材料性能与老化时间、老化温度之间存在着特定的关系，利用热空气加速老化的方法对材料进行试验，按照老化经验公式即可计算出常温下的橡胶使用寿命[24]。

老化特性指标y与老化时间t之间存在如下经验公式：

y=Be-Kta

(1)

式中，y为老化特性指标；B为试验常数；K为老化速度常数，d-a；t为老化时间，d；a为经验常数，介于0～1之间。

老化速度常数K与老化温度T的关系可用阿累尼乌斯(S.A.Arrhenius)公式表示为

K=Ae-E/RT

(2)

式中，E为表面活化能， J/mol；R为气体常数，J/(K·mol)；T为老化试验温度，K ；A为频率因子，d-a。

3 管片接缝防水密封垫橡胶材料老化试验

3.1 试验设备及方法

试验主要设备为高温老化箱、压缩夹具。高温老化箱型号为LR300BF，压缩夹具按GB/T 7759.1—2015的要求制作。

测试橡胶密封垫在不同高温下的压缩永久变形量。对应的老化特性指标yc按式(3)计算：

(3)

式中，h0为试样初始高度，mm；h1为试样恢复后的高度，mm。

在标准实验室环境下，将规格尺寸为Φ13 mm×6.3 mm的橡胶试样在5个试验温度(70 ℃、80 ℃、90 ℃、100 ℃、110 ℃)条件下，测定试样高度随时间的变化情况。具体方法如下：

(1) 将橡胶密封垫上好夹具放置24 h；

(2) 卸去夹具并静置24 h后测定密封垫高度，作为试样的初始高度h0；

(3) 将带有夹具的试样放入老化试验箱中，恒温一段时间后取出，卸去夹具后静置24 h，用游标卡尺测量试样高度h1。

3.2 测试结果

三元乙丙橡胶密封垫试样在5个试验温度条件下老化特性指标yc汇总见表1。

表1 不同温度下三元乙丙橡胶密封垫老化特性指标

4 试验结果分析

4.1 分析方法

式(1)、式(2)的回归属于第二类非线性回归问题。对式(1)作变换Y=lny，a=-K，b=lnB，X=tα，得

Y=aX+b

(4)

对式(2)作变换k=lnK，c=-E/R，d=lnA，t=1/T，得

k=ct+d

(5)

变换后可进行一元线性回归，但因含有未知经验常数α，需要采用逐次逼近方法进行求解，计算总残差平方和。

总残差平方和

(6)

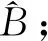
(7)

式中，n为样本总数；r为相关系数。

温度To时老化预测的随机误差δ为

(8)

温度To时老化速度常数K的预测上限为

(9)

综上，可得温度To时密封垫使用寿命的预测值：

(10)

4.2 数据处理编程

对密封垫的使用寿命的预测，需要对两个公式的5个参数进行最小二乘的计算。为使总残差平方和最小，涉及对经验常数α值的反复试算，运算量极大。为此，基于M语言编制了相应的计算程序，用于预测密封垫的使用寿命，程序流程如图3所示。

图3 使用寿命预测程序流程

4.3 老化性能预测

通过程序对试验数据的计算，得到最优解下的经验常数α=0.771，总残差平方和I=0.013 4。各个温度下的速度常数K和经验常数B见表2。

表2 不同温度下的速度常数K和经验常数B

图4 不同温度下密封垫老化特性指标实测数据及拟合曲线

对阿累尼乌斯公式拟合得到单侧显著性水准为0.01时对应的参数计算结果见表3。

表3 各参数计算值

老化速度常数K与老化温度T的实测数据及拟合曲线如图5所示。随着老化温度的增加，密封垫老化速度常数显著增长。

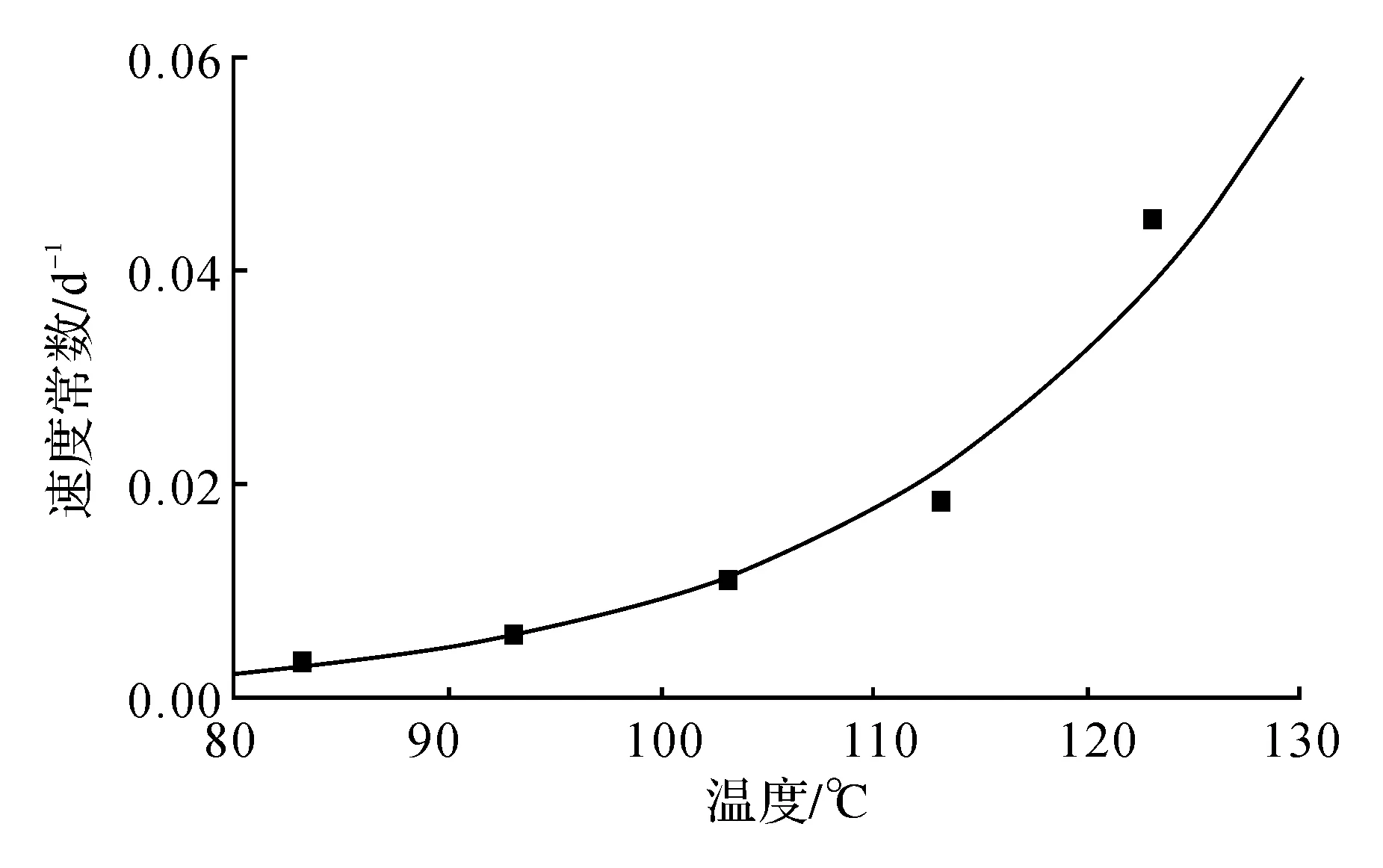
图5 密封垫老化速度常数与老化温度的实测数据及拟合曲线

5 密封垫老化数值模拟

5.1 数值模拟计算模型

管片密封垫槽和三元乙丙橡胶密封垫的相互作用按照平面应变问题考虑，采用ABAQUS建立二维数值计算模型。模型中管片和密封垫均采用实体单元进行模拟，下部管片底部采用固定约束条件、上部管片顶部采用位移约束条件，模拟管片张开量的变化。管片尺寸为300 mm×100 mm，管片及密封垫共划分13 156个单元和 14 114个节点，计算模型如图6所示。

5.2 模型参数选取

管片为C50混凝土，采用弹性模型模拟，弹性模量取34.5 GPa，泊松比取0.2。

密封垫属于橡胶类材料，具有弹性、大应变的特性，在连续介质力学中采用超弹性Mooney-Rivlin模型来表征[25]。该模型的变形能密度函数表达式为[26-27]

W=C10(I1-3)+C01(I2-3)

(11)

式中，I1、I2为变形张量；C10、C01为材料常数。

该模型需要确定C01、C10两个参数。由于橡胶材料具有不可压缩性，泊松比υ按0.5考虑，弹性模量与C01及C10具有如下关系[28]：

(12)

此外，弹性模量和硬度存在如下关系[29]：

(13)

式中，H为邵氏硬度，A。

密封垫老化前的硬度为64，由此可以得到C01=0.142，C10=0.568。密封垫老化后，考虑密封垫的弹性模量变化服从寿命预测函数，可知100年后其等效弹性模量降低为原值的0.57倍，由此可以得到C01=0.082，C10=0.326。

采用TIE约束，模拟密封垫槽与密封垫底边的胶结作用；采用摩擦接触，模拟其余接触面的相互作用。其中，密封垫与管片间的摩擦系数设为0.5，密封垫自身的摩擦系数设为0.3。

5.3 计算结果分析

通过数值计算，在管片接缝张开量为6 mm时，密封垫的应力分布如图7所示。

图7 密封垫的应力分布情况

对密封垫接触面的表面应力数据进行提取，绘制密封垫老化前后的应力曲线，如图8所示。

老化前后的应力曲线表明，当密封垫发生老化后，其表面接触应力明显降低，约为原值的0.57倍。对密封垫防水失效的判定基于密封垫的表面接触应力[30-31]。由此可知，密封垫在老化后，其防水性能下降。因此，在密封垫设计时应考虑老化因素对其防水性能的降低，将密封垫的设计耐水压力至少提高至原设计水压的1.75倍。

图8 老化前后密封垫的表面应力

6 结 论

本文采用时温等效原理对密封垫橡胶材料开展加速老化试验研究，分别测试了5个温度(80 ℃、90 ℃、100 ℃、110 ℃、120 ℃)条件下密封垫的压缩永久变形量，并开展了密封垫老化的相关数值模拟。主要结论如下：

(1) 通过对暗挖装配式管片接缝密封垫的老化性能试验数据的回归分析，得出了密封垫使用寿命为134年的结论。论证了选用的密封垫橡胶，其使用寿命满足隧道设计使用年限100年设计要求。可选用该类三元乙丙橡胶材料作为暗挖装配式隧道管片接缝的密封垫。

(2) 在密封垫橡胶材料数据处理过程中，用M语言编制了相关计算程序，降低了数据处理的难度，提高了分析老化试验数据的效率。

(3) 密封垫与管片间相互作用的数值计算结果表明，在隧道服役100年后，密封垫的表面接触应力降低至原值的0.57倍。因此，在密封垫设计时应考虑老化因素的影响，将密封垫的设计耐水压力至少提高至原设计水压的1.75倍。