采用滑模条件积分的无人驾驶汽车弯道超车路径规划与跟踪控制

张家旭周时莹施正堂赵 健朱 冰

(1.吉林大学汽车仿真与控制国家重点实验室,吉林长春 130022;2.中国第一汽车集团有限公司智能网联研发院,吉林长春 130011;3.浙江亚太机电股份有限公司智能汽车控制系统研究院,浙江杭州 311200)

1 引言

无人驾驶汽车是汽车行业的重大技术创新之一,可以有效缓解交通拥堵压力和大幅降低交通事故率,并且随着汽车智能化的不断升级,无人驾驶汽车必将会产生更大的社会效益.由于无人驾驶汽车利用感知系统获取周围环境信息,自动规划路径并控制汽车实现无人驾驶的目的[1],因此,路径规划与跟踪控制是无人驾驶汽车的重要组成部分,已成为汽车行业研究的热点问题之一.

在无人驾驶汽车路径规划研究领域中,已有的研究成果大致可划分为基于约束优化的路径规划算法[2–3]、基于几何曲线的路径规划算法[4–5]和基于搜索的路径规划算法[6].文献[2]将无人驾驶汽车避让静止障碍物路径规划问题转化为贝塞尔曲线参数的约束优化问题,并采用具有全局搜索能力的遗传算法对其进行求解,得到满足避让约束条件的可行路径.文献[4]采用Sigmoid函数规划无人驾驶汽车避让静止障碍物路径,并建立Sigmoid函数参数与汽车侧向加速度、汽车侧向加速度变化率和避障距离约束条件的映射关系,使规划的避让路径满足汽车安全性和舒适性需求.文献[5]采用斜坡函数和正弦函数相叠加的方式设计无人驾驶汽车高速换道避让路径,虽然算法具有较好的实时性,但未考虑汽车侧向加速度的影响.上述研究成果均是针对静止障碍物规划无人驾驶汽车的避让路径,适用场景具有较大的局限性.为此,文献[3]采用六次多项式曲线将无人驾驶汽车避让动态障碍物路径规划问题描述成六次多项式曲线参数的约束优化问题,通过在每一个采样时刻在线求解该约束优化问题得到避让动态障碍物的可行平滑路径.文献[6]在Frenet坐标系下基于五次多项式曲线建立一系列轨迹作为无人驾驶汽车路径规划算法的搜索空间,并从安全性、舒适性和可行性角度建立每条轨迹的惩罚函数,将遍历搜索算法得到的惩罚函数最小的轨迹作为目标轨迹.基于约束优化的路径规划算法和基于搜索的路径规划算法虽然可以针对动态障碍物规划避让路径,但算法通常较复杂,在计算过程中需要较多的硬件资源.

由于无人驾驶汽车是一个高度非线性的复杂系统,在无人驾驶汽车路径跟踪控制研究领域,国内外学者主要采用对外界干扰和模型不确定性具有强鲁棒性的控制方法设计路径跟踪控制策略.文献[7–8]采用线性二自由度汽车动力学模型和汽车运动学模型相结合的方式构建预测模型,并采用模型预测控制方法设计无人驾驶汽车路径跟踪控制策略.模型预测方法虽然对外界干扰和模型不确定性具有较强的鲁棒性,但基于模型预测方法设计的无人驾驶汽车路径跟踪控制策略需要在每一个采样时刻在线求解一个有限时域开环优化问题,极大的增加了无人驾驶汽车路径跟踪控制策略的计算量.为此,文献[9]采用µ综合方法设计无人驾驶汽车路径跟踪控制策略.虽然基于µ综合方法设计的无人驾驶汽车路径跟踪控制策略可以保证闭环系统在最坏情况下稳定运行,但在控制性能方面存在较大的保守性.为了提高无人驾驶汽车路径跟踪控制性能,文献[10–11]采用滑模控制方法设计无人驾驶汽车路径跟踪控制策略,但滑模控制方法固有的抖振问题降低了无人驾驶汽车路径跟踪的平顺性.

鉴于此,本文针对无人驾驶汽车弯道超车场景,基于五次多项式曲线提出一种路径规划算法,以及基于滑模条件积分控制方法提出一种路径跟踪控制策略.首先,将无人驾驶汽车弯道超车路径分解成驶入超车道路径、保持超车道内行驶路径和驶回原车道路径3部分,并基于五次多项式曲线分别规划出满足汽车侧向加速度约束和动态障碍物避障约束的驶入超车道路径和驶回原车道路径,3 部分路径平滑连接构成无人驾驶汽车弯道超车路径.随后,利用滑模条件积分控制方法设计无人驾驶汽车路径跟踪控制策略,使闭环系统不但可以保留传统滑模控制方法对外界干扰和模型不确定性具有强鲁棒性的优点,而且可以有效避免传统滑模控制方法固有的抖振问题,进而提升闭环系统的响应特性.最后,仿真验证所提出的无人驾驶汽车路径规划算法和路径跟踪控制策略的可行性和有效性.

2 路径规划

无人驾驶汽车弯道超车路径通常由驶入超车道路径、保持超车道内行驶路径和驶回原车道路径3部分组成[12],如图1所示.

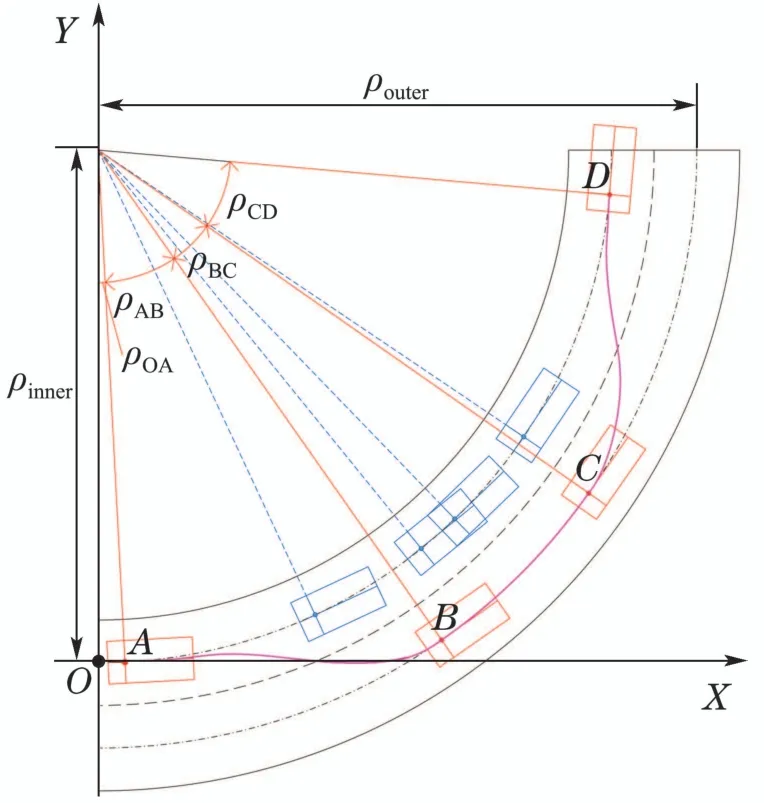
图1 汽车弯道超车路径Fig.1 Path planning for corner overtaking of a car

建立固定坐标系XOY,已知原车道和超车道的曲率分别为ρinner和ρouter,假设初始时刻本车和前方低速行驶汽车均在原车道匀速行驶,二者的速度分别为vH和vG,并且本车在与前方低速行驶汽车相距为SAB的点A处开始沿着基于五次多项式曲线规划的驶入超车道路径安全、平稳的行驶到点B.为了避免本车在驶入超车道过程中与前方低速行驶汽车发生碰撞,驶入超车道路径AB经历的最大时间为

由式(1)可知:点B的选取原则是保证本车驶入超车道后依然位于前方低速行驶汽车的后方,采用相对保守策略获得本车驶入超车道过程的绝对安全性.同时,基于式(1)描述的驶入超车道路径AB经历的最大时间,可得驶入超车道路径AB对应的最大圆弧角度为

假设本车在点A处的方位角为θOA,则点A和点B的坐标可分别表示为

采用五次多项式曲线将驶入超车道路径AB表示为

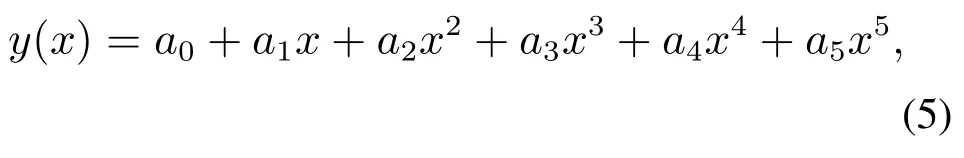
式中a0,a1,……,a5为驶入超车道路径AB的待定系数.

为了简化驶入超车道路径AB待定系数的计算过程,以及避免计算过程产生奇异问题,将驶入超车道路径AB沿向量平移长度和顺时针旋转θOA角度,得到与驶入超车道路径AB几何形状相同的曲线段其端点坐标分别为

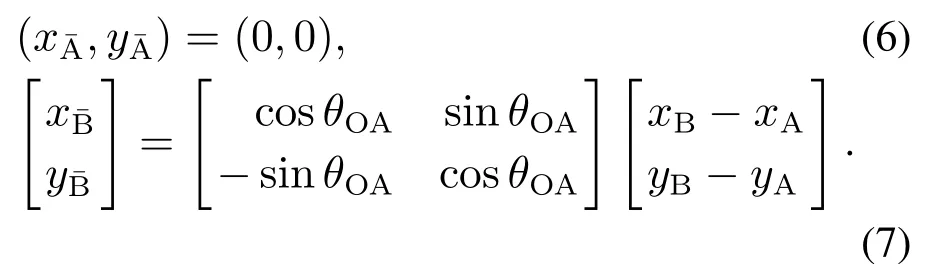
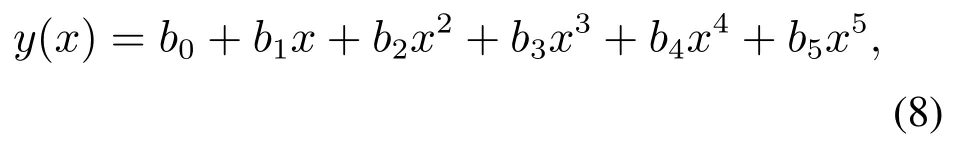
式中b0,b1,……,b5为曲线段的待定系数.

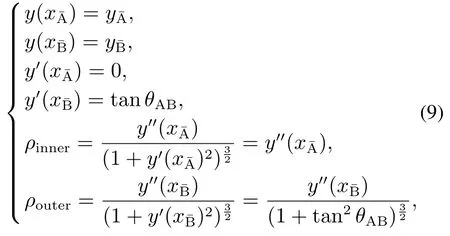
离散采样基于五次多项式曲线规划的驶入超车道路径AB,并利用式(10)检测驶入超车道路径AB的每一个离散采样点是否满足汽车侧向加速度约束.

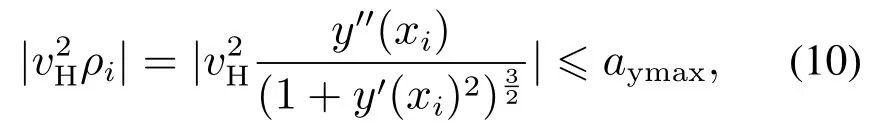
式中:aymax为驶入超车道路径AB允许的最大汽车侧向加速度;xi为驶入超车道路径AB上离散采样点.

若规划的驶入超车道路径AB不满足汽车侧向加速度约束,则增加本车与前方低速行驶汽车之间的距离SAB,采用式(1)–(9)重新规划驶入超车道路径AB,直到规划的驶入超车道路径AB满足式(10)描述的汽车侧向加速度约束为止.

为了避免本车在驶回原车道过程中与前方低速行驶汽车发生碰撞,本车驶入超车道并在超车道内行驶一段时间后再执行驶回原车道操作.假设本车在超车道内行驶的时间为

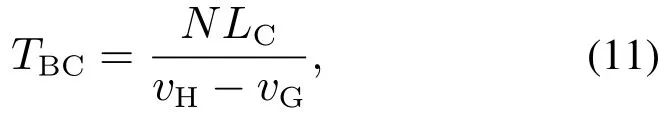
式中:N为正整数;LC为前方低速行驶汽车的车长.

由式(11)可知:点C的选取原则是保证本车超越前方低速行驶汽车NLC长度后再执行驶回原车道操作,采用相对保守策略获得本车驶回原车道过程的绝对安全性.同时,基于式(11)描述的本车在超车道内行驶的时间,可得保持超车道内行驶路径BC对应的圆弧角度以及驶回原车道路径起始点C的坐标为

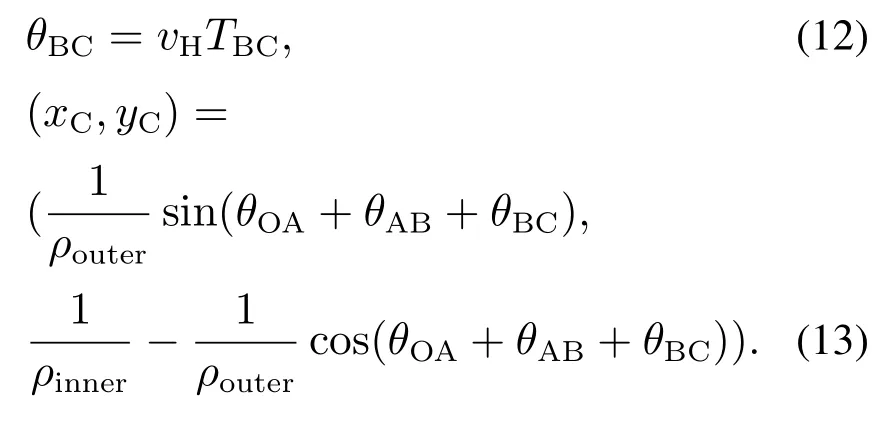
假设本车沿着基于五次多项式曲线规划的驶回原道路径从点C到点D的行驶距离为SCD,则利用式(1)–(10)描述的计算步骤即可规划出满足汽车侧向加速度约束的驶回原道路径CD,故不再赘述.

3 路径跟踪控制

在无人驾驶汽车弯道超车路径规划过程中,通过汽车侧向加速度约束将汽车的操纵特性限制在线性工作区域,使得无人驾驶汽车在弯道超车过程中产生的质心侧偏角较小.因此,为了使设计的路径跟踪控制策略简洁高效,本节以如图2所示的汽车运动学模型为基础,建立包含系统加性不确定性的汽车弯道超车路径跟踪控制模型[13].

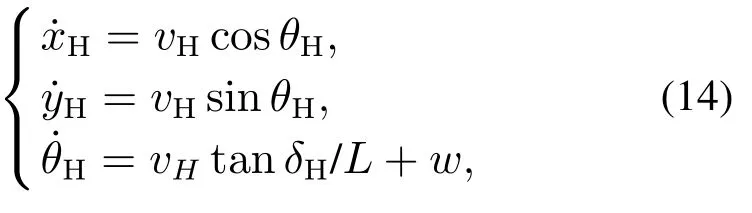
式中:xH,yH和θH分别为汽车后轴中点横向坐标、纵向坐标和汽车方位角;δH和L分别为汽车前轮转向角和轴距;w为系统的加性不确定性,包括:轮胎侧偏特性未建模动态、转向未建模动态和悬架未建模动态等.

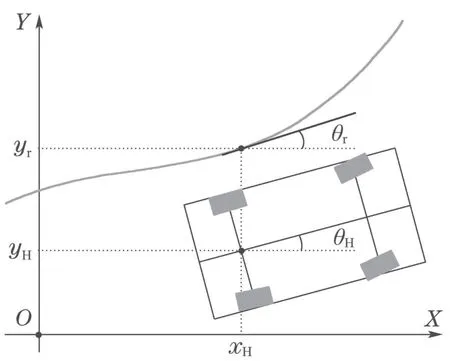
图2 汽车运动学模型Fig.2 Vehicle kinematics model

如图2所示,考虑汽车后轴中点横向坐标的变化率始终为正,将xH作为非时间参考量,则式(14)描述的三维路径跟踪控制模型可简化为以yH与其目标值yr的偏差和θH与其目标值θr的偏差作为状态量的二维路径跟踪控制模型.

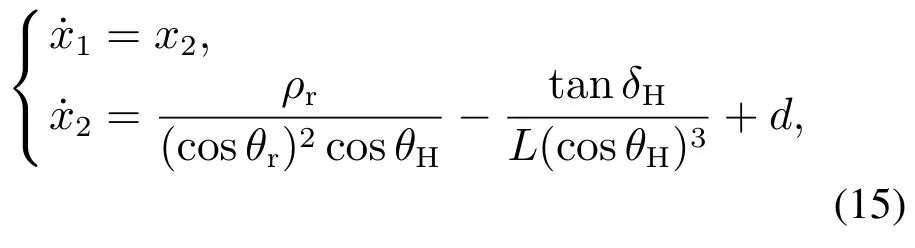
式中:x[x1x2]T[yr−yHtanθr−tanθH]T;d−w/(vH(cosθH)3)为系统的复合干扰.假设系统复合干扰幅值有界,则有

鉴于系统复合干扰是产生路径跟踪误差的主要原因,可假设系统复合干扰的变化率满足如下约束:

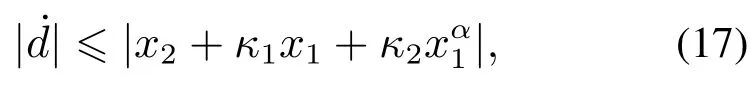
式中κ0>0,κ1>0,κ2>0和α>1为设计参数.

针对汽车弯道超车路径跟踪控制律的目标,定义汽车弯道超车路径跟踪误差为

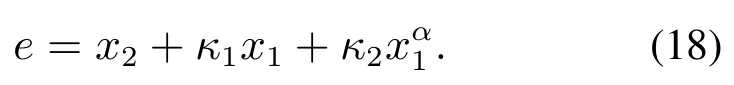
由汽车弯道超车路径跟踪误差定义如下包含条件积分项的滑模面

式中:κ3>0为设计参数;σ为条件积分项,并且满足

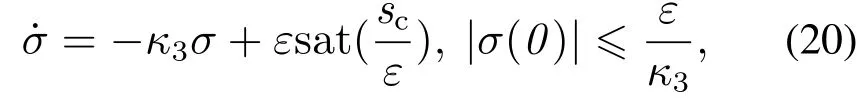
式中:ε>0为设计参数;sat(·)为饱和函数.

由文献[14]可知:式(20)描述的条件积分项包含于不变集Dσ{|σ|≤ε/κ3},并且式(20)中的饱和函数满足

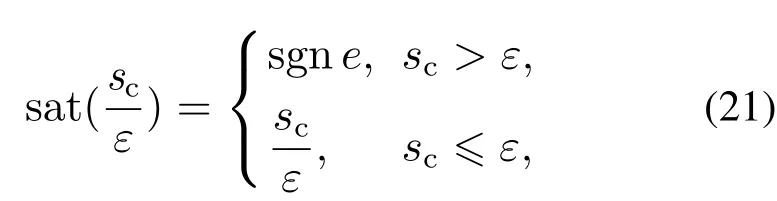
式中sgn为符号函数.

下面基于式(19)描述的包含条件积分项的滑模面设计汽车弯道超车路径跟踪控制律,并得到定理1.

定理1考虑式(15)描述的系统,设计如下汽车弯道超车路径跟踪控制律:

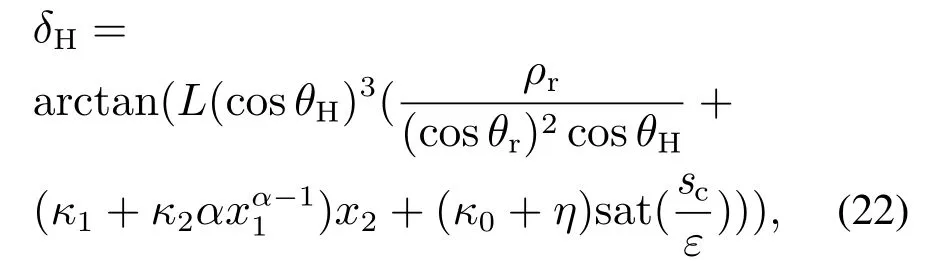
式中η >0为设计参数.给定参数κ4>0,若设计参数κ0>0,κ3>0,ε>0和η >0满足

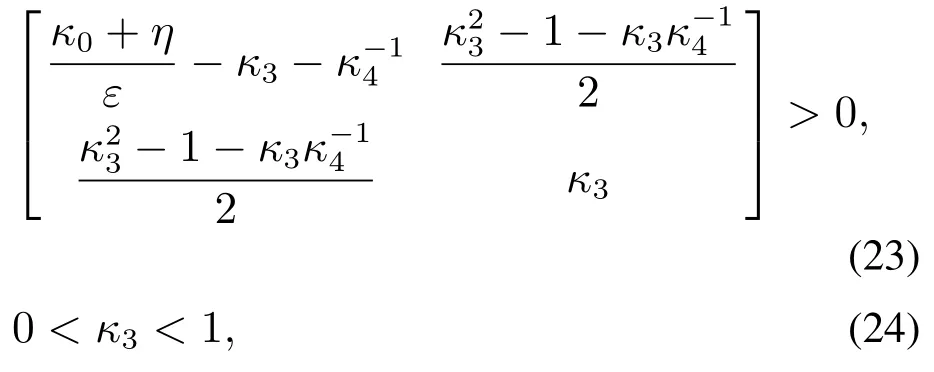
则汽车弯道超车路径跟踪控制闭环系统的状态轨迹渐近收敛到平衡原点x0.

证由于式(22)包含的饱和函数为分段连续函数,故分两步证明汽车弯道超车路径跟踪控制闭环系统的状态轨迹渐近收敛到平衡原点.当sc>ε时,证明汽车弯道超车路径跟踪控制闭环系统的状态轨迹在有限时间内收敛到区域Dε{(e,σ):|sc|≤ε}.由于式(20)描述的条件积分项包含于不变集Dσ{|σ|≤ε/κ3},故仅需证明汽车弯道超车路径跟踪误差在有限时间内收敛到区域Dε{(e,σ):|sc|≤ε}即可.为此,定义李雅普诺夫候选函数为

对式(25)求导,可得

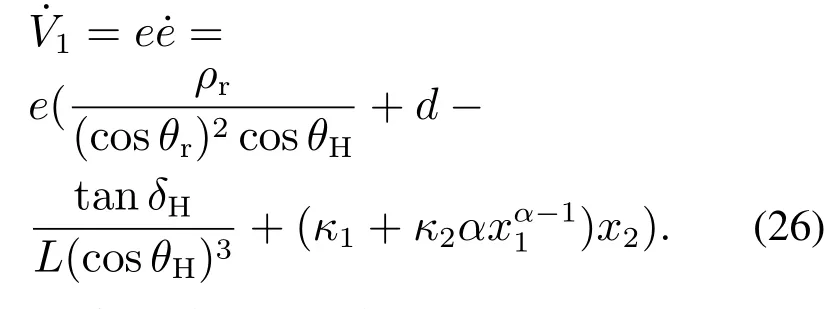
将式(22)代入式(26),可得

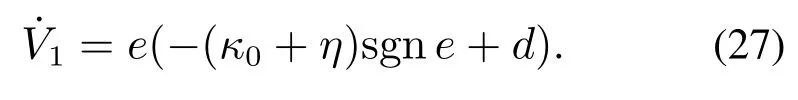
由约束条件式(16),可知

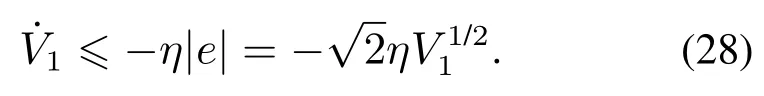
因此,当sc>ε时,汽车弯道超车路径跟踪控制闭环系统的状态轨迹在有限时间内收敛到区域Dε{(e,σ):|sc|≤ε},并且停息时间满足T(e0)≤

当sc≤ε时,证明汽车弯道超车路径跟踪控制闭环系统的状态轨迹渐近收敛到平衡原点.首先,利用式(19)描述的包含条件积分项的滑模面将汽车弯道超车路径跟踪控制闭环系统转化为

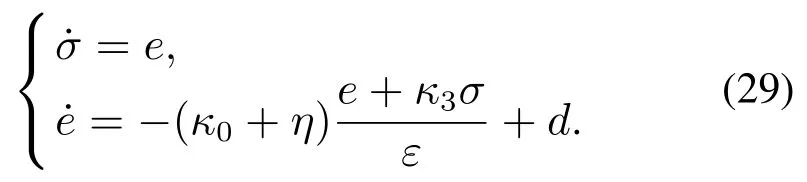
为了量化式(29)描述的闭环系统状态轨迹的平衡点,设计如下非线性干扰观测器:

式中:z1为非线性干扰观测器的内部状态量;为系统复合干扰d的估计.

为了证明非线性干扰观测器估计误差是一致最终有界的,定义如下李雅普诺夫候选函数:

式中edd −为非线性干扰观测器估计误差.

对式(31)求导,可得

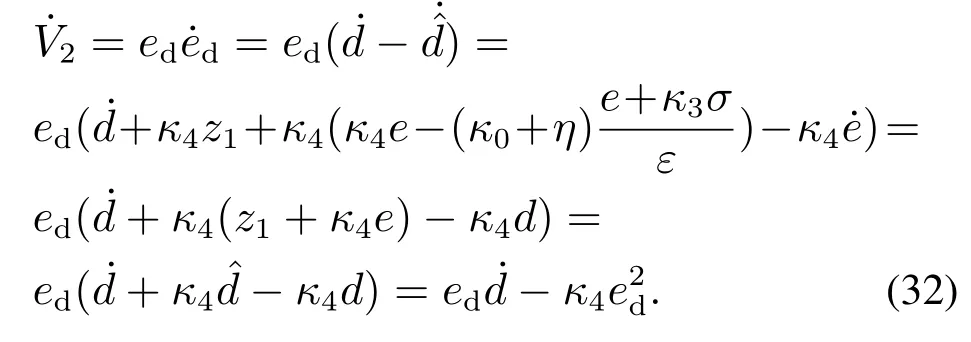
由约束条件式(17),可知

将不等式(33)代入式(32),可得

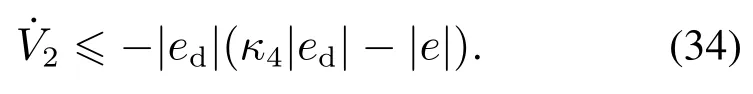
因此,非线性干扰观测器的估计误差是一致最终有界的,并且满足

下面以非线性干扰观测器的估计输出为基础,证明式(29)描述的闭环系统状态轨迹渐近收敛到

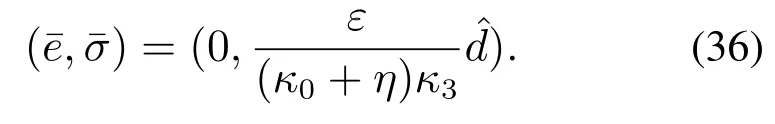
为此,定义李雅普诺夫候选函数为

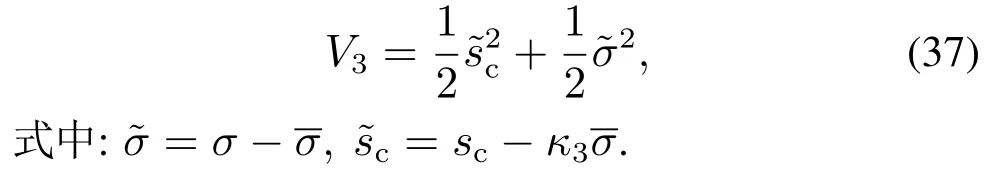
对式(37)求导,可得

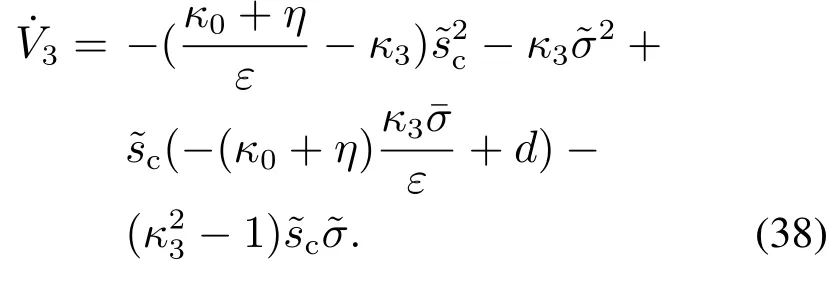
将式(36)代入式(38),可得

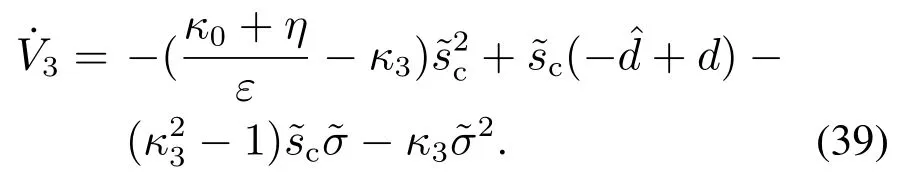
将不等式(35)代入式(39),以及由约束条件式(24),可得

由约束条件式(23),可知:式(29)描述的闭环系统状态轨迹渐近收敛到同时,由汽车弯道超车路径跟踪误差定义式(18),可知

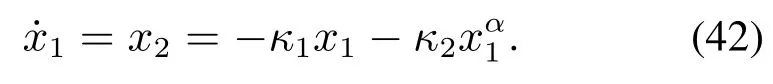
由式(42)可知,当sc≤ε时,汽车弯道超车路径跟踪控制闭环系统的状态轨迹渐近收敛到平衡原点x0.同时,当x1远离平衡原点时,式(42)右端的幂函数项远大于线性函数项,因此,幂函数项主要用来驱动汽车弯道超车路径跟踪控制闭环系统的状态轨迹加速收敛到平衡原点邻域内;当x1在平衡原点邻域内时,式(42)右端的线性函数项远大于幂函数项,因此,线性函数项主要用来避免汽车弯道超车路径跟踪控制闭环系统的状态轨迹在平衡原点邻域内产生颤振现象.

从定理1的证明过程可知,当sc>ε时,所设计的汽车弯道超车路径跟踪控制律为传统滑模控制律,对系统的复合干扰具有较好的鲁棒性;当sc≤ε时,所设计的汽车弯道超车路径跟踪控制律类似于PI控制律,对系统的复合干扰依然具有较好的鲁棒性,并且避免了传统函数控制方法采用饱和函数消除抖振现象而导致的控制品质降低问题.因此,定理1描述的汽车弯道超车路径跟踪控制律可以使汽车后轴中点纵向坐标和汽车方位角快速收敛到其目标值.

4 仿真结果及分析

本节首先采用m语言编程实现基于五次多项式曲线设计的汽车弯道超车路径规划算法,并将该算法中的原车道和超车道半径分别设置为500 m和503.75 m,驶入超车道路径允许的最大汽车侧向加速度和驶回原车道路径允许的最大汽车侧向加速度分别设置为4 m/s2和3 m/s2,保证汽车在弯道超车过程中的操纵特性始终位于线性工作区域.随后,在MATLAB/Simulink环境下导入汽车弯道超车路径规划算法的输出结果,并利用MATLAB/Simulink的模块库编程实现汽车弯道超车路径跟踪控制策略,将其与车辆动力学软件CarSim无缝连接构成模型在环仿真系统来验证所提出的汽车弯道超车路径规划算法与跟踪控制策略的有效性.在仿真验证过程中,汽车弯道超车路径跟踪控制策略的参数分别设置为κ06,κ12,κ25,κ30.35,κ417,α3,η1和ε0.01,与斯坦福大学提出的斯坦利方法[15]的仿真对比结果如图3–5所示.

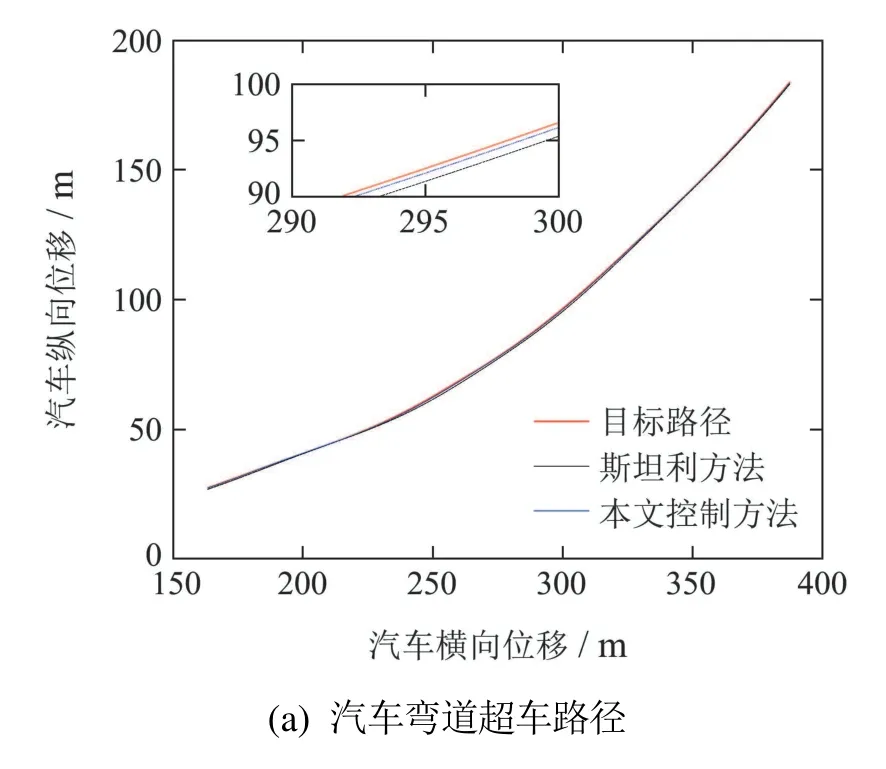
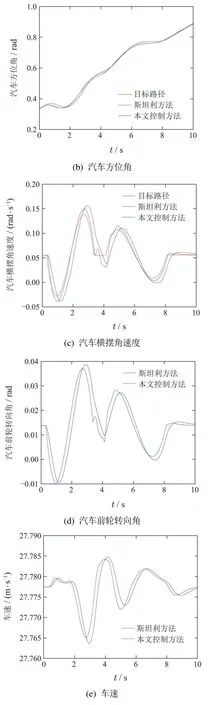
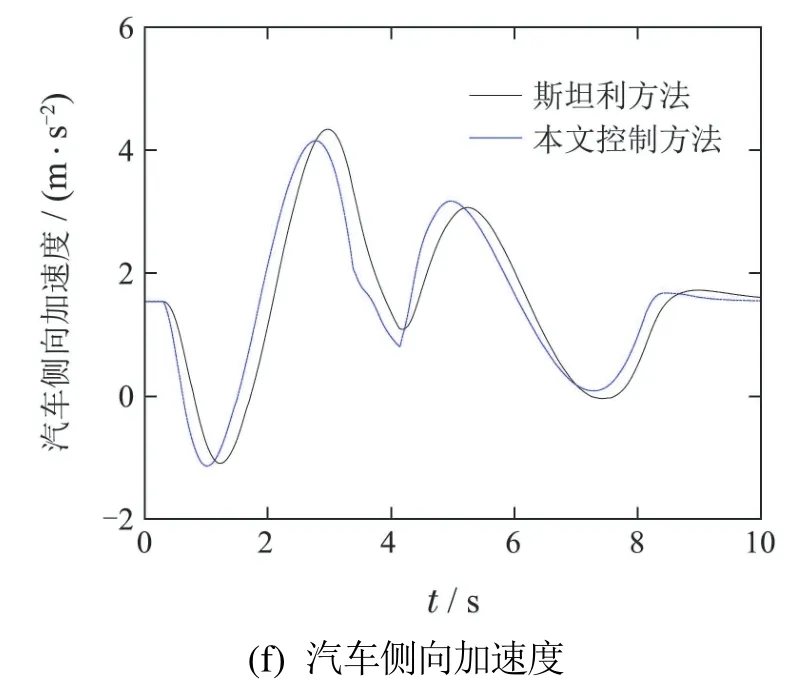
图3 汽车弯道超车行驶状态信息Fig.3 Vehicle driving status on corner overtaking

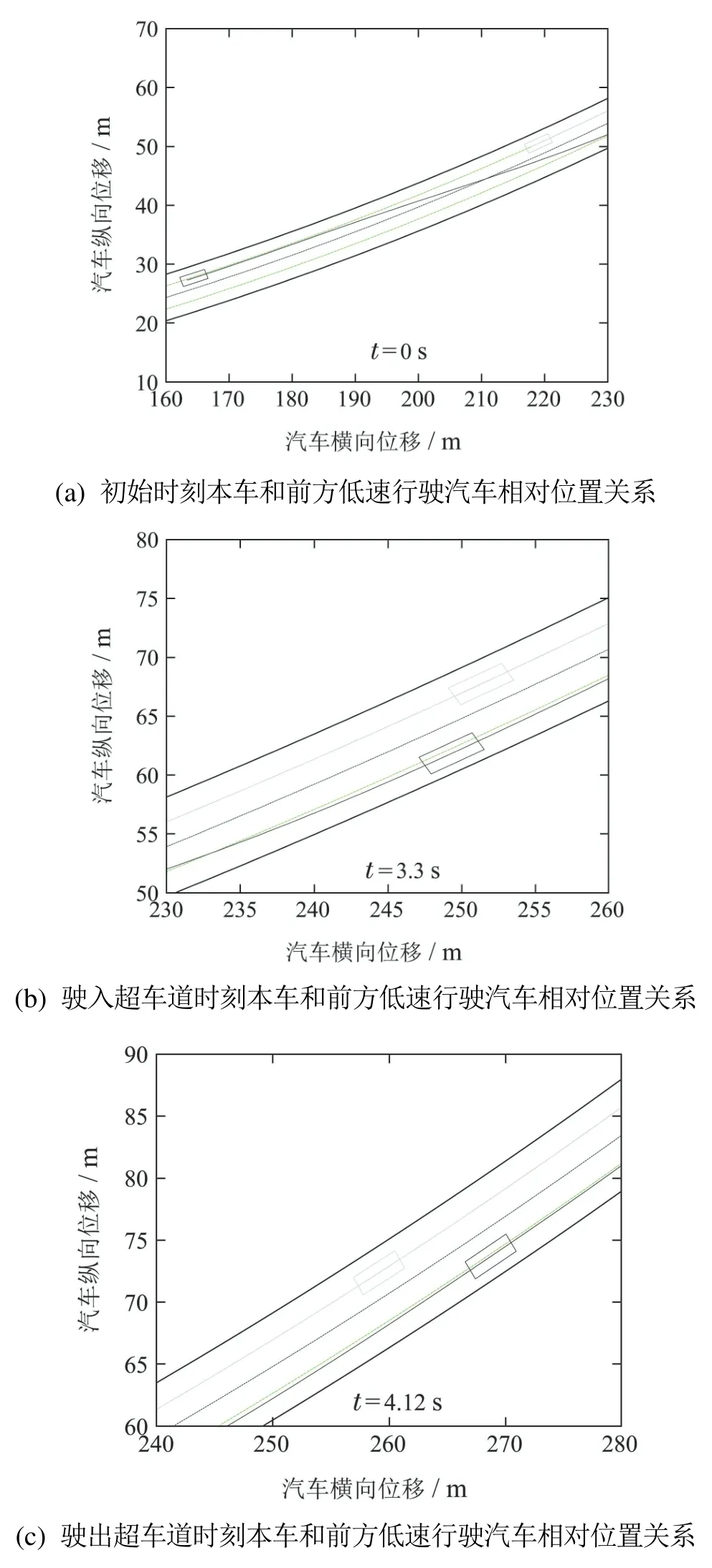
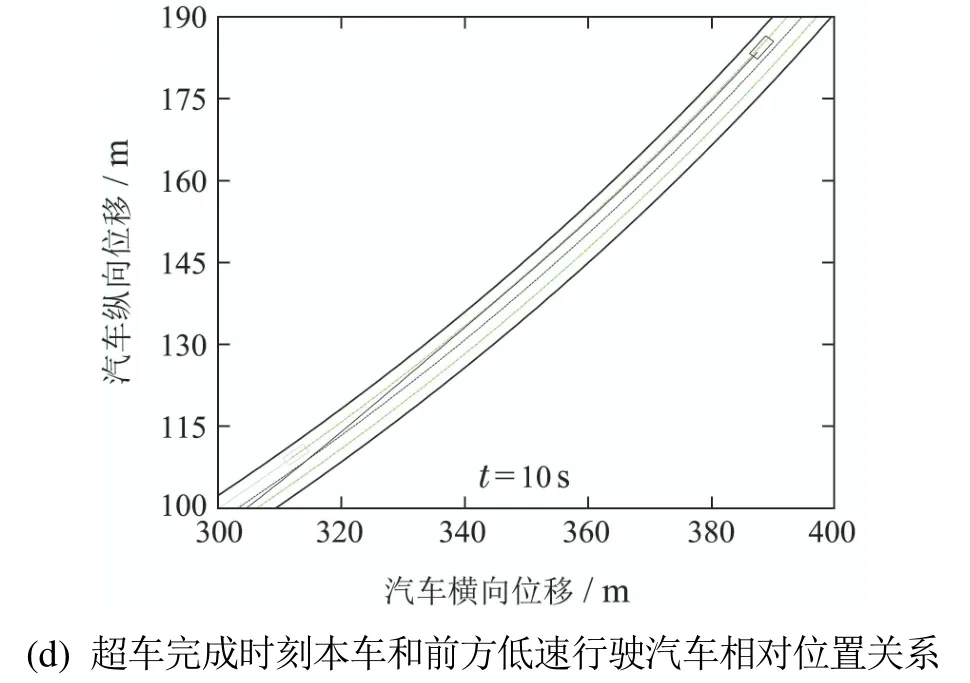
图4 本文控制方法的路径跟踪控制仿真结果Fig.4 Simulation results of proposed path tracking method

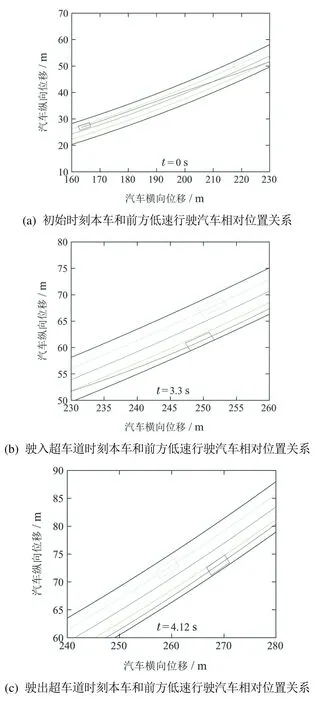
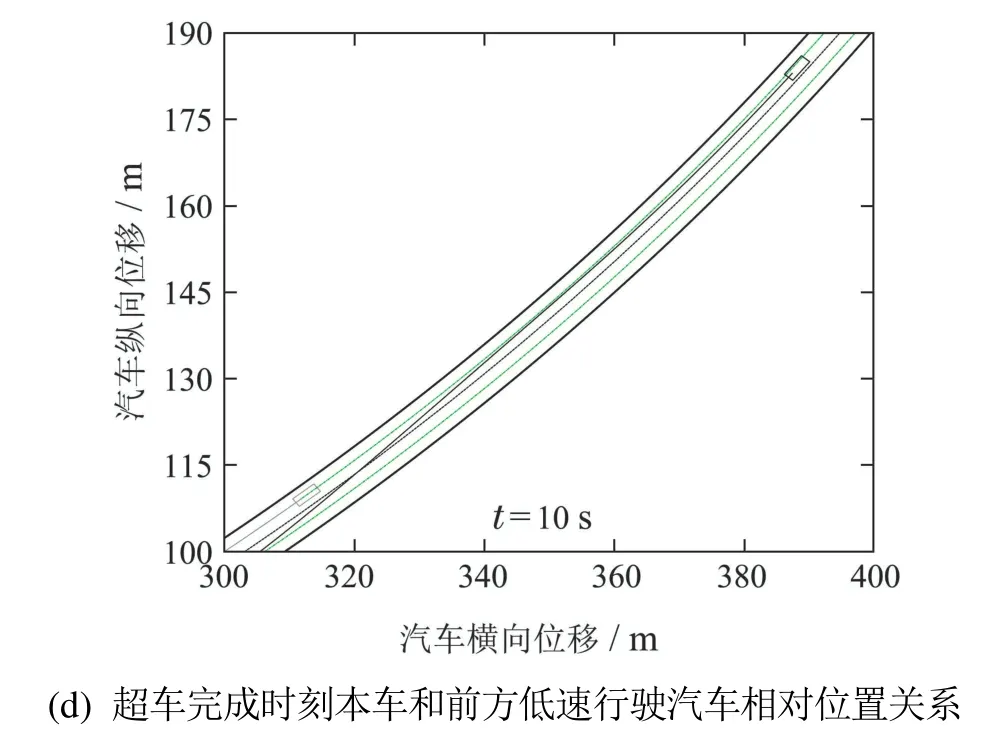
图5 斯坦利方法的路径跟踪控制仿真结果Fig.5 Simulation results of Stanley path tracking method

如图3(a)–(d)、图4和图5所示,本文控制方法和斯坦利方法均可以使汽车无碰撞的、稳定无抖振的跟踪汽车弯道超车目标路径和目标方位角,实现汽车弯道超车工况,但本文控制方法的跟踪精度更高,尤其从汽车驶入超车道和驶回超车道时的本车和前方低速行驶汽车相对位置关系可以更直观的看出,采用本文控制方法的汽车和采用斯坦利方法的汽车均位于超车道内,并且与前方低速行驶汽车保持一定的安全距离,但是采用本文控制方法的汽车与超车道中心线的距离更小,进一步说明本文控制方法的跟踪精度更高.如图3(c)–(f)、图4和图5所示,相对于斯坦利方法,本文控制方法具有更快速的动态响应特性,从而使汽车在8 s之后可以更快速、更稳定的驶回原车道.采用文献[16]的残差计算方法量化分析得到,本文控制方法对应的汽车后轴中点纵坐标和方位角跟踪残差分别为0.27%和0.79%,而斯坦利方法对应的汽车后轴中点纵坐标和方位角跟踪残差分别为0.75%和1.69%,这表明本文控制方法具有更高的跟踪精度.

5 结论

1) 基于五次多项式曲线设计无人驾驶汽车弯道超车路径规划算法.首先,将无人驾驶汽车弯道超车路径分解成驶入超车道路径、保持超车道内行驶路径和驶回原车道路径3部分,简化无人驾驶汽车弯道超车路径规划过程.随后,基于五次多项式曲线分别规划出满足汽车侧向加速度约束和动态障碍物避障约束的驶入超车道路径和驶回原车道路径,将3部分路径平滑连接构成无人驾驶汽车弯道超车路径.

2) 基于滑模条件积分控制方法设计无人驾驶汽车路径跟踪控制策略.首先,构建包含系统加性不确定性的汽车运动学模型,并以汽车后轴中点横向坐标为非时间参考量,将其转化为包含系统复合干扰的非时间参考名义模型.以此为基础,利用滑模条件积分控制方法设计具有强鲁棒性优点且无抖振的无人驾驶汽车路径跟踪控制策略,并采用李雅普诺夫稳定性理论证明其收敛性.

3) 仿真验证所提出的无人驾驶汽车路径规划算法和路径跟踪控制策略的可行性和有效性,结果表明:所提出无人驾驶汽车路径规划算法和路径跟踪控制策略可以引导无人驾驶汽车安全、舒适的完成弯道超车操作,并且相对于斯坦利方法,具有更快的响应速度和更高的跟踪精度.