车辆路径问题的轻鲁棒优化模型与算法

孙 亮潘全科邹温强王亚敏

(1.上海大学机电工程与自动化学院,上海 200072;2.山东理工大学交通与车辆工程学院,山东淄博 255049;3.南京审计大学信息工程学院,江苏南京 211815)

1 引言

车辆路径问题(vehicle routing problem,VRP)是指在满足一定的约束条件(如需求量、车辆容量等)下,配送中心构造有限条车辆运行路径为客户提供配送服务,最终实现客户服务水平和运输成本等决策目标的最优化.配送完成时间是衡量客户服务水平的一个重要因素.但配送完成时间受交通拥堵等多种因素的影响,很难通过精确的概率分布进行描述,使得随机规划方法[1]处理不确定旅行时间条件下的车辆路径问题(vehicle routing problem with uncertain travel times,VRP–UT)的效果不够理想.与随机规划方法不同,鲁棒优化方法[2]利用不确定数据集的边界关系,可以将不确定的优化模型转化为确定的优化模型进行求解.目前常用的最坏场景鲁棒优化方法[3],要求所有车辆均需要在客户指定的时间内将货物送达客户,但从实际营运角度看,稍微偏离客户允许时间范围的配送服务并不对服务水平构成影响.轻鲁棒优化方法[4–7]通过对鲁棒优化模型中的某些约束进行松弛,以约束违背最小化为优化目标,从而改善最坏实现下目标函数值与预期值之间的偏差.所以采用轻鲁棒优化方法研究VRP–UT,更具有理论意义和实际价值.

从求解算法看,求解此类问题的算法主要有邻域搜索算法[8–10]、分支定界算法[11–13]和超启发式算法[14]等.现有算法主要关注总变动成本的降低,但对如何在总变动成本降低的同时,使尽可能多的客户在其允许的时间范围完成配送服务关注较少.基于上述分析,建立了一种描述VRP–UT特征的轻鲁棒优化模型(light-robust-optimization model,LRO),提出了一种超启发式粒子群算法(hyper particle swarm optimization,HPSO).大量的仿真实验表明了所提模型和算法的有效性.

2 问题描述

VRP–UT描述如下:给定完全赋权图G(V,E)表示配送中心与客户点之间的相对位置关系,其中V{0,1,2,……,n}表示点集,

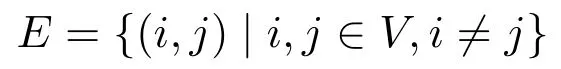
表示边集,0 表示配送中心;CV{0}表示顾客集.配送中心拥有相同容量的m辆车,每辆车的最大负载均为Q,车辆集合用K{1,2,……,m}表示.配送车辆的单位惩罚成本ω1和单位等待成本ω2,第i个顾客的需求量di,客户允许的服务时间窗(客户时间窗)[ETi,LTi].关于旅行时间的不确定数据集UT定义如下:

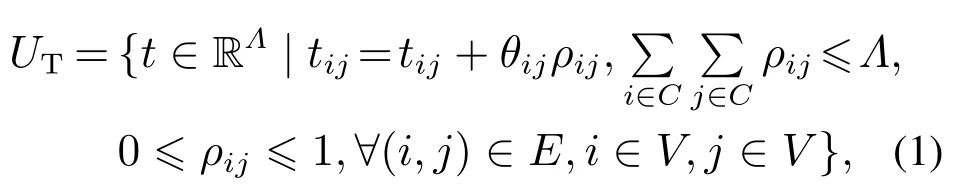
车辆从客户i到客户j的旅行时间在之间任意取值.

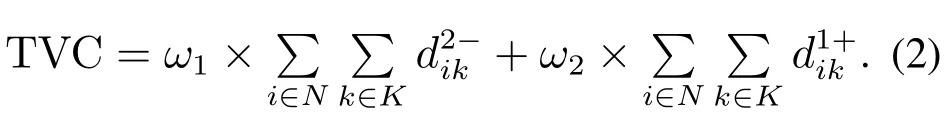
根据已知决策信息,获取一个调度方案,该调度方案具有两个特征:①对UT内的任意实现均保持可行;②该调度方案对应的TVC最小.

条件假设如下:车辆从配送中心出发,服务完最后一个客户后,必须回到配送中心;车辆进入某个客户点,也必须从该点离开;一辆车可以为多个客户服务,但一个客户只能被一辆车服务;车辆的实际负载不得超过Q.

3 VRP–UT轻鲁棒优化模型

在文献[15]给出的鲁棒优化模型的基础上,利用新增加的松弛变量表示变动成本,构建描述该问题特征的轻鲁棒优化模型.模型中M表示一个充分大的正数.LRO模型如下:

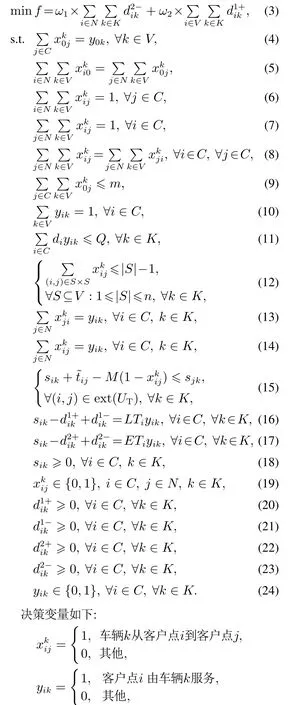
目标函数(3)表示TVC;约束(4)–(5)表示每辆车必须从配送中心出发,服务完最后一个客户后,回到配送中心;约束(6)–(8)表示车辆服务完某个客户后,必须从该客户离开;约束(9)表示配送中心允许使用的最大车辆数限制;约束(10)表示每个客户只能由一辆车进行服务;约束(11)表示每一辆车的实际负载不能超过Q;约束(12)为避免出现子循环(客户点之间形成的环路)约束;约束(13)–(14)表示决策变量之间的关系;约束(15)表示可行解对于UT的任意实现均保持可行;约束(16)–(17)表示车辆到达客户的时间几乎处处在[ETi,LTi]内;约束(18)–(24)表示决策变量的取值范围.

4 LRO的求解方法

从LRO可行解满足的条件可以看出,LRO可行解的每一个子回路都是一个环,而深度优先搜索(depth first search,DFS)[16]是搜索图中是否存在回路的有效的遍历方式.因此,以是否存在零环(可行解中某条子回路的TVC为零,则称该子回路为零环)为搜索目的的DFS可以发现零环.与此同时,使用DFS生成零环时,当遍历到某个结点的前驱结点为已经访问过的结点时,将不再访问这个结点,因此可以完全避免子循环的产生.

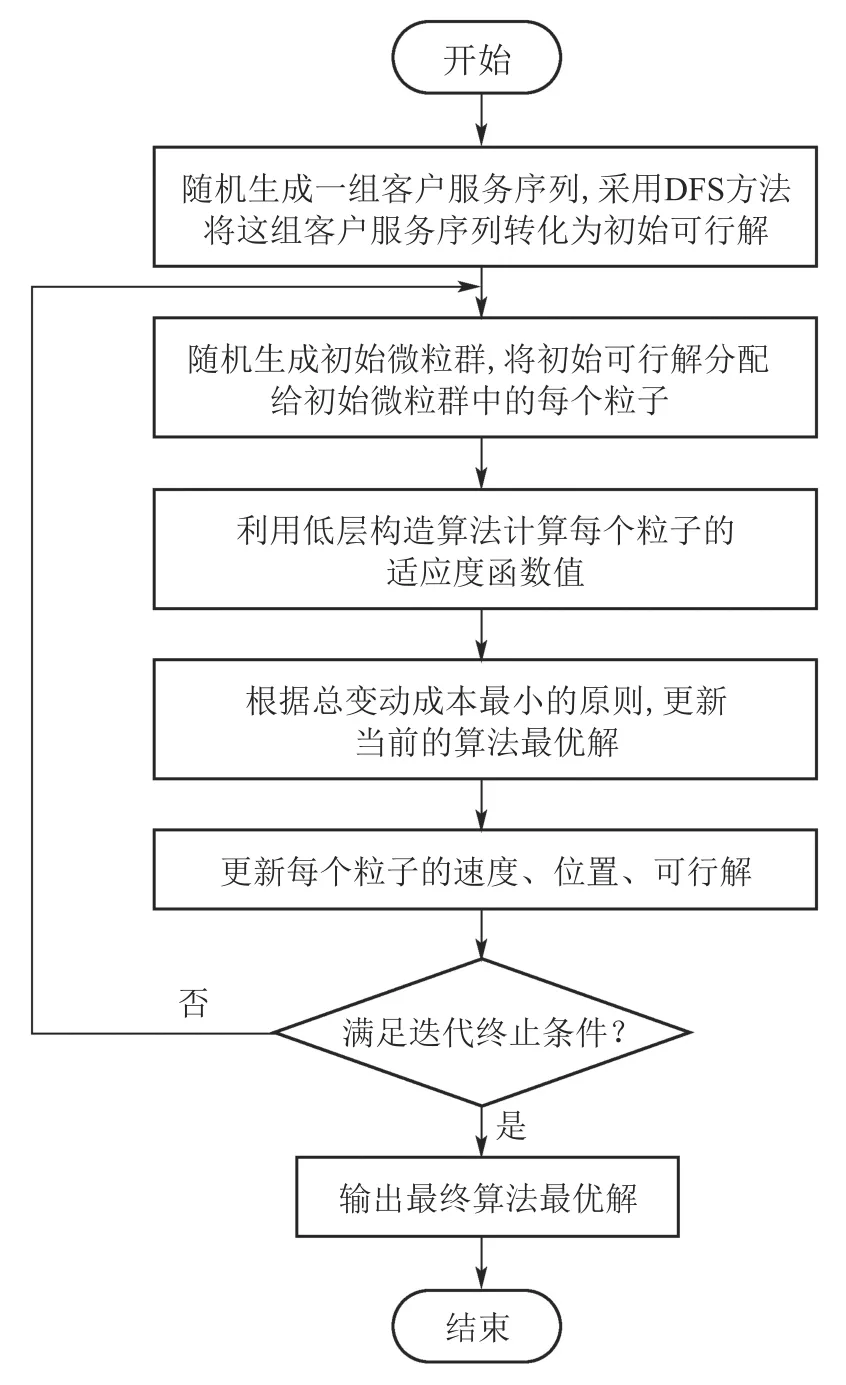
图1 HPSO算法流程图Fig.1 Flow chart of HPSO

因为PSO可以兼顾寻优过程的全局探测和局部开采能力并且没有许多的参数调节,所以采用PSO作为外层搜索算法.HPSO的算法流程如图1所示.

4.1 DFS的实现方法

1) 可行解的编码方式(encoding of feasible solutions).

可行解采用基于客户顺序的编码方法,如图2所示.0表示配送中心.其他数字表示客户点.例如,路径(0 2 6 7 9 4 0)表示车辆服务客户的顺序是0→2→6→7→9→4→0.

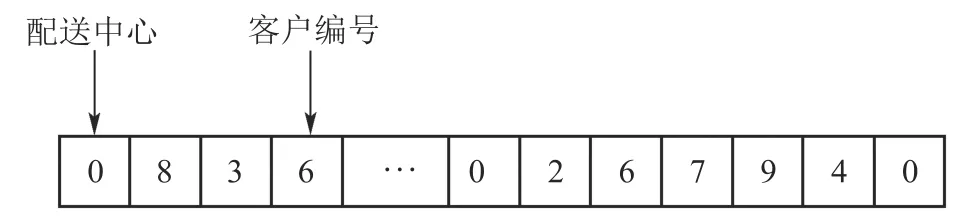
图2 可行解编码结构示意图Fig.2 Feasible solution representation

2) DFS的算法步骤(pseudo-code of DFS).

DFS由两层循环构成.内层循环利用DFS,产生一个零环.在内层循环中,从0点开始,如果发现一个未访问的及时点,该点不是0点并且该点不违背约束(9),该点加入第k辆车对应的服务序列中,并从该点继续搜索,直到形成第k个零环zk.将发现的及时点从客户服务序列MSi1,……,ik,……,in中移除.在外层循环中,将zk加入所有子回路的集合R中.重复此过程,直到无法在MS 中发现及时点.剩余的点根据约束式(11)插入到R中.sumdemand(zk)表示zk的总需求.Γ(·)表示某个点的邻接点.DFS(MS)算法的伪代码如下:

4.2 低层启发式规则变换方式设计

根据几何不等式,如果每条子路径上的TVC尽可能相同,那么TVC将得到进一步改善.从这个角度出发,对文献[14]中提出的启发式规则变换方式进行重新设计.新的启发式规则变换方式的具体实施步骤如下:

2) LRO–insert.分别从TVC 最大和最小的两个环中随机选择位置qm和qh,将客户服务序列中对应的元素从总变动成本最大的路径中移除,然后将该位置的元素插入到客户服务序列中qm对应的元素前面;

3) LRO–inverse.首先,随机选择一个环.其次,从该环中随机选择两个位置kr和kq,将该序列中kr和kq之间的所有位置对应的元素kr,kr+1,……,kq−1,kq变换为kq,kq−1,……,kr+1,kr.

4.3 粒子的编码与解码

4.3.1 粒子的编码与解码

粒子是一个1×3q维向量.采用1,2,3分别表示LRO–swap,LRO–inverse,LRO–insert这3种变换方式.第1,4,……,3q −2维表示变换方式,其他维度表示变换位置.q表示启发式规则的数量.例如,(1,2,8)表示将初始可行解对应的客户服务序列中的第2位和第8位采用LRO–swap的方式进行交换.

4.3.2 粒子的解码方法

记P(r1,……,rq)表示位置向量.依次将启发式规则ri作用于该粒子对应的可行解,得到最终的客户服务序列后,再使用DFS将该序列转化为一个可行解计算的TVC.

4.4 更新规则

因为位置向量表示的低层构造算法是根据给定的启发式规则的变换方式生成,而不是对给定启发式规则的进行对换,所以现有用于VRP求解的粒子群优化算法(particle swarm optimization,PSO)的更新规则不能直接应用于LRO的求解.因此需要对更新公式进行重新设计.重新设计的更新式如下:

从结构变动度来看，至2016年，真正体现医务人员服务价值的费用项目，如手术费、护理费，这两项明细费用项目的构成比较往年有所增加并达到五年来的最高值，反映了该院在提升医者服务价值、提高医务人员积极性方面已有一定进步；但灰色关联数据显示，手术费及护理费两项指标的关联系数逐年下降，这说明二者与住院次均费用之间关系的紧密程度有所减弱。建议卫生管理者在制定完善医疗服务价格调整政策时，参考国内相关的标化价值方法学体系[11]，明确技术劳务、物资耗材等项目的价值构成，逐步理顺医疗服务价格，充分调动医务人员工作积极性；而医疗机构应继续提高医生业务收入中技术劳务性收入比重，进一步优化费用结构。

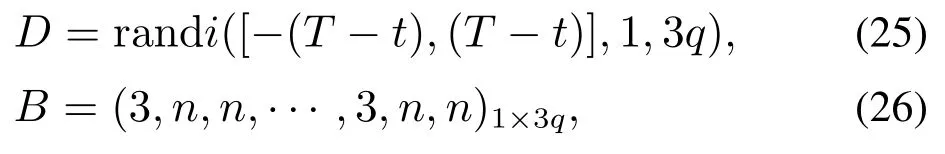
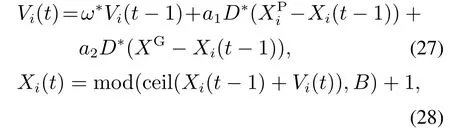
其中:t表示当前迭代次数;ceil(·)表示向上取整函数;mod(·)为取余函数;Xi(t){xi1(t),……,xi3m(t)}为粒子i在第t代的位置向量;

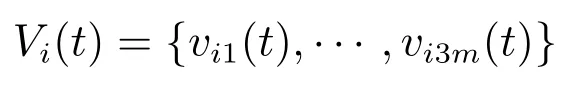
为粒子i在第t代的速度向量;为当前迭代次数下,种群中适应度函数值中最好的个体位置向量;XG为截至到当前迭代次数,种群中所有中最好的个体位置向量;ω为惯性权重;T为迭代的最大次数;M为种群规模;a1,a2为加速因子;D为随机生成[−(T −t),(T −t)]之间的3m个正整数.

4.5 HPSO的算法步骤

首先,使用DFS方法生成一组初始可行解.其次,随机生成初始粒子群.将可行解分配到每一个粒子中.然后,进入迭代阶段,在该阶段,利用重新设计的更新公式,进行迭代,根据TVC最小的原则,更新当前最优解.当满足迭代终止条件时,输出最终的最优解.HPSO(LRO)算法的伪代码如下所示:

利用DFS方法得到一组初始可行解

5 仿真分析

5.1 算例选取与参数设置

从文献[16]中选取若干标准算例,引入UT的参数信息,构造新算例用于分析LRO和HPSO的相关性能.算例的基本信息详见表1.

表1 标准算例的基本信息Table 1 Configure information of benchmarks

tij表示标准算例中到的旅行时间.令ω1,a11,a21,M30,T30,q10,ω11,ω21,Vmin−30,Vmax30,ρij1.参数取上述值的原因是便于观察合理的计算时间内算法优化解的相关性能.为了避免正态分布和方差齐性假设对分析结果的影响,本文选择Kruskal-Wallis ANOVA检验和趋势卡方检验对算法优化解的相关性能进行分析.

5.2 仿真环境

采用MATLAB R2016a(64bit)实现了求解LRO 的HPSO及其他对比算法,在Intel(R)Core(TM)i5–6200U CPU@2.3 GHz,8 GB内存的计算机上进行了仿真实验.相关统计学检验使用SPSS(version 26)实现(SPSS的全称为statistical product and service solutions,即:统计产品与服务解决方案).

5.3 LRO与RO比较分析

文献[15]给出的鲁棒优化模型(robust optimization model),记为RO.两者在模型特征上的差异,可能造成两者最优解(TVC为0的解)对UT参数的灵敏度不同.由于LRO与RO的目标函数不同,对于RO,只利用其约束条件发现最优解,对两者的最优解进行灵敏度分析.

从文献[16]中选取35个标准算例进行最优解的灵敏度分析.选取算例及其特征如表2所示.参数信息如表3所示.采用HPSO对表2中的每个算例运算30次,记录各自的TVC.表2中加粗部分表示该算例两种鲁棒优化方法均发现理想最优解.分别将LRO和RO获得的最优解代入不同的Λ和θij,观察其TVC的变化.Λ从0.25n增加到n,增加幅度为0.125n.ρij1,maxt表示算例中tij的最大值.θij从maxt增加到4 maxt,增加幅度为0.5 maxt.

表3–4说明,当Λ和θij发生变化时,RO在最坏实现下的最优解,其TVC随着Λ和θij的增加而改变,并且这种改变具有统计学意义(P <0.05).LRO在最坏情况下的最优解,虽然也发生一定改变,但这种改变并没有统计学意义(P >0.05).与RO不同,LRO是通过不断调整偏差值产生的最优解,这可能是LRO对参数变化不敏感的一个重要原因.

表2 算例类型及其算例对应表Table 2 Feature of benchmark

表3 Λ的变化对TVC的影响(θijρij 1.5 max t,M30,T 30)Table 3 Λ impact on TVC (θijρij 1.5 max t,M 30,T 30)

表3 Λ的变化对TVC的影响(θijρij 1.5 max t,M30,T 30)Table 3 Λ impact on TVC (θijρij 1.5 max t,M 30,T 30)

表4 θij的变化对TVC的影响(Λ0.75∗n,M30,T 30)Table 4 θij impact on TVC(Λ0.75∗n,M30,T30)

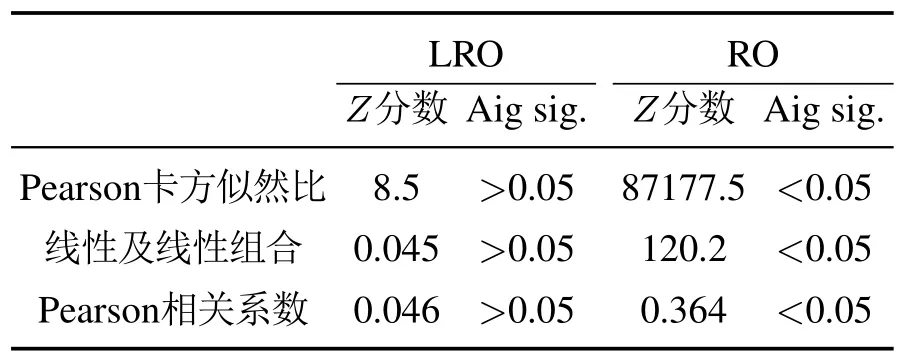
表4 θij的变化对TVC的影响(Λ0.75∗n,M30,T 30)Table 4 θij impact on TVC(Λ0.75∗n,M30,T30)

5.4 HPSO的求解性能分析

因为文献[9]中的求解算法(简记为AMP)是目前普遍认为求解此类鲁棒优化模型性能非常理想的启发式算法,所以本文采用AMP与HPSO进行对比试验.为了避免初始解生成策略对分析结果的影响,两者均采用DFS方法生成初始解.两个算法遍历的可行解总数相同.HPSO的参数设置详见第4.1节.针对表5中的测试数据,使用HPSO和AMP分别独立求解30次LRO.将30次运算结果的运行时间(t),TVC的95%置信区间记录于表5中.针对表5中描述的数据进行Kruskal-Wallis ANOVA检验,相关结论见表6.

表6中关于两种算法的TVC的平均秩次说明,HPSO获取的TVC显著小于AMP获取的TVC(p<0.05).HPSO获取的TVC能够显著改善的原因是:AMP根据给定的启发式规则产生可行解;HPSO在搜索过程中不断生成新规则产生可行解.因此,HPSO搜索范围更加广泛,从而提升了算法优化解的性能.

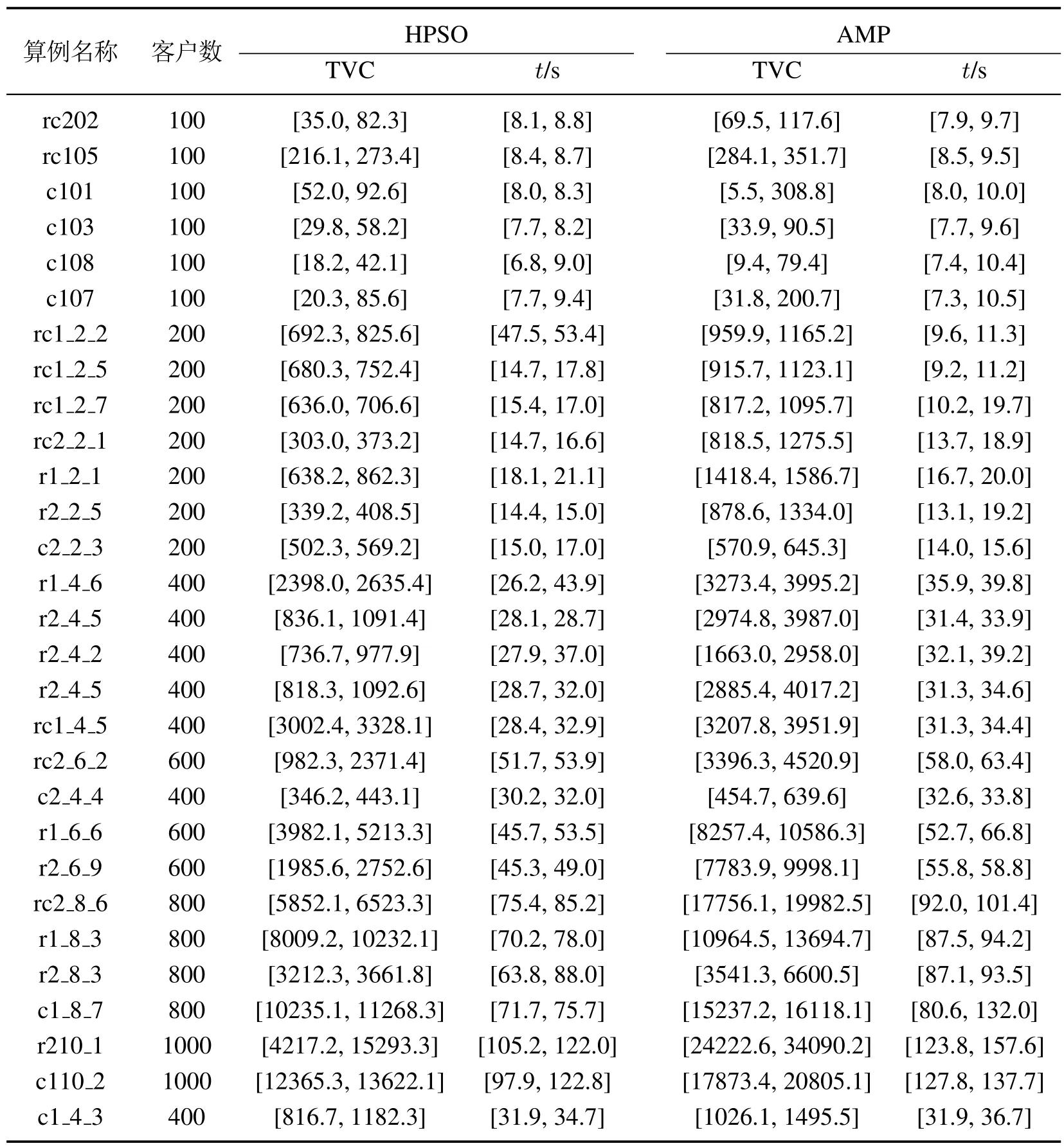
表5 TVC与运算时间分析Table 5 Detailed results of TVC and Time

表6中关于两种算法运行时间的平均秩次说明,两种算法在求解LRO时运行时间不存在统计学差异(p>0.05),造成这种现象的原因是两者的算子本质上都属于对换,在时间复杂度上是相同的.

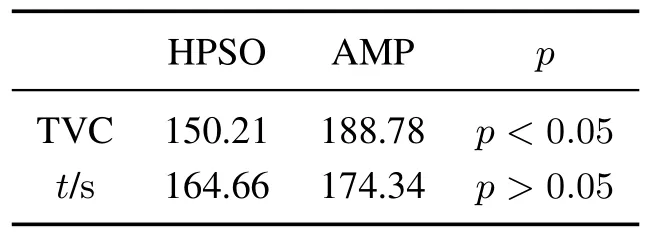
表6 针对TVC和时间的平均秩次比较分析Table 6 Results of mean ranks with regard to TVC and time

6 结论

本文的核心内容如下:①模型方面,以TVC最小为优化目标,构建描述该问题特征的LRO;②算法方面,设计HPSO求解LRO,该算法利用DFS策略生成初始解,然后再利用重新设计的更新公式,生成构造算法,进一步降低算法优化解对应的TVC;③仿真实验表明,HPSO是一种求解LRO的有效算法.