球头弹体侵彻舰船板架加强筋时的攻角变化简化理论模型*

姚熊亮，王 治，叶墡君，吴子奇，王志凯

（1.哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨150001；2.中国兵器工业集团航空弹药研究院有限公司，黑龙江 哈尔滨150001）

反舰导弹是目前对于舰船打击的有力武器。半穿甲战斗部反舰导弹通过战斗部侵彻多层甲板或舱壁，然后在舰船内部爆炸，对舰船造成结构或功能毁伤，其侵彻能力是影响战斗部性能的重要因素。舰船结构的特点在于其由板架结构组合而成，板架结构由薄板和纵横交错的加强筋构成。目前，对弹体侵彻薄板问题已有大量理论和实验研究，形成了较为成熟的理论体系[1-2]。然而，由于舰船板架结构的特殊性，均质薄板侵彻力学模型不能直接应用于弹体侵彻板架结构加强筋问题。板架结构加强筋的腹板高度甚至可达到几十厘米，加强筋对于弹体侵彻、特别是弹体攻角变化具有较大影响，而攻角过大往往是弹体侵彻失败的重要因素。因此，对于加强筋对弹体侵彻能力影响的研究具有重要意义。

目前对于舰船板架结构侵彻问题的研究较少。在实验方面，张中国等[3]针对单层和多层带加强筋的结构靶进行了弹体侵彻实验，建立了弹体侵彻结构靶板的剩余速度公式，发现加强筋对靶板吸收能量、变形和破坏形式有很大影响。段卓平等[4-5]对单层带加强筋的结构靶进行了正侵彻和斜侵彻实验，在弹丸侵彻均质靶板理论基础上，给出了弹丸对加筋结构靶侵彻的终点弹道理论计算模型。姚熊亮等[6]报道了实尺度舰船多层板架结构侵彻实验，并提出了板架结构剩余速度一种改进的理论公式，并与实验结果进行了验证。

对于板架结构侵彻的力学模型方面，宋卫东等[7]将半穿甲战斗部侵彻加筋靶板的过程分为冲塞过程和花瓣型扩孔过程2个主要阶段，在此基础上提出了侵彻力学模型。宋卫东等[7-8]采用动量守恒定理研究了截卵型刚性弹体对加筋靶板的侵彻贯穿问题，提出了力学模型并预测了剩余速度。展婷变等[9]采用动量守恒定理，分析了截卵型弹体正侵彻加强筋结构靶的过程，得出了弹体剩余速度与位移、侵彻位置等物理量的关系。巨圆圆等[10]利用能量守恒原理给出了尖卵形弹丸侵彻十字形加筋靶板的花瓣型破坏模式下剩余速度计算公式。徐双喜等[11]针对截锥形弹正侵彻加筋靶板问题，计及了面板花瓣形破坏、腹板塑性变形、翼板翻转变形等能量，根据能量守恒原理推导了弹体的剩余速度和弹道极限速度。

然而，目前板架结构侵彻理论模型主要针对剩余速度，且多以均质薄板侵彻模型通过等效处理而建立，无法预报弹体攻角变化。考虑到加强筋对弹体攻角影响较大，本文中将加强筋简化为刚塑性梁模型，建立弹体运动与梁运动耦合控制方程，进而给出弹体攻角变化理论求解公式。

1 理论模型

定义战斗部着角β 为弹体质心运动方向与目标板架结构法线的夹角，攻角φ为弹体轴线与质心运动方向的夹角，如图1所示。

弹体质心初速度为v0，侵彻后的质心剩余速度为vr，战斗部侵彻过程中时间为t。

本文主要研究对象为超音速反舰导弹侵彻舰船板架结构的相关问题，具体来讲，反舰导弹弹体质量大（与子弹和破片相比），速度为高速侵彻（Ma≈2），板架结构为舰船板架（薄板加筋结构）。针对此问题作出如下假设：

（1）弹体的弹着点为加强筋中点，以便考察加强筋对弹体姿态角的改变作用。

（2）弹头形状为半球形，弹体为刚体。

（3）由于加强筋处以加筋为主要承力结构，忽略平板的作用，将加强筋视为刚塑性梁模型。

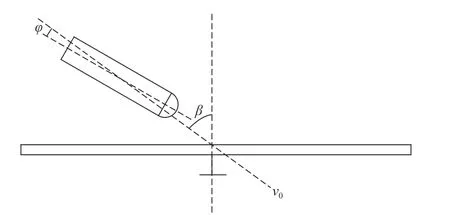
图1 着角与攻角示意图Fig.1 Schematic diagram of impact angle and attack angle

（4）加强筋与弹道面垂直，即运动为二维的。

（5）加强筋实际边界条件介于固支与简支之间，加强筋长度较长，弹体侵彻时间短，侵彻过程中弯曲应力波未传至边界，加强筋可视为无限长梁，而塑性铰在侵彻过程中沿着梁移动。

（6）加强筋发生拉伸破坏，这种假设对于尖头弹或球头弹造成的花瓣破坏是合理的，对于平头弹造成的剪切破坏是不适用的。

通过以上假设将弹体侵彻加筋板问题转化为弹体侵彻刚塑性梁问题，简化后的模型如图2所示。由于对称性，弹体在x-y 平面作二维平面运动。其中水平方向x 为弹体速度方向，靶面法线与水平方向夹角为初始着角β0。弹体的质心为C，其头部距质心的距离为Lc。为了建立理论模型方便，定义弹体转角α 为弹体轴线与水平方向的夹角。弹体接触靶板之前，其速度方向就是水平方向，因此初始转角α0等于弹体初始攻角φ0。

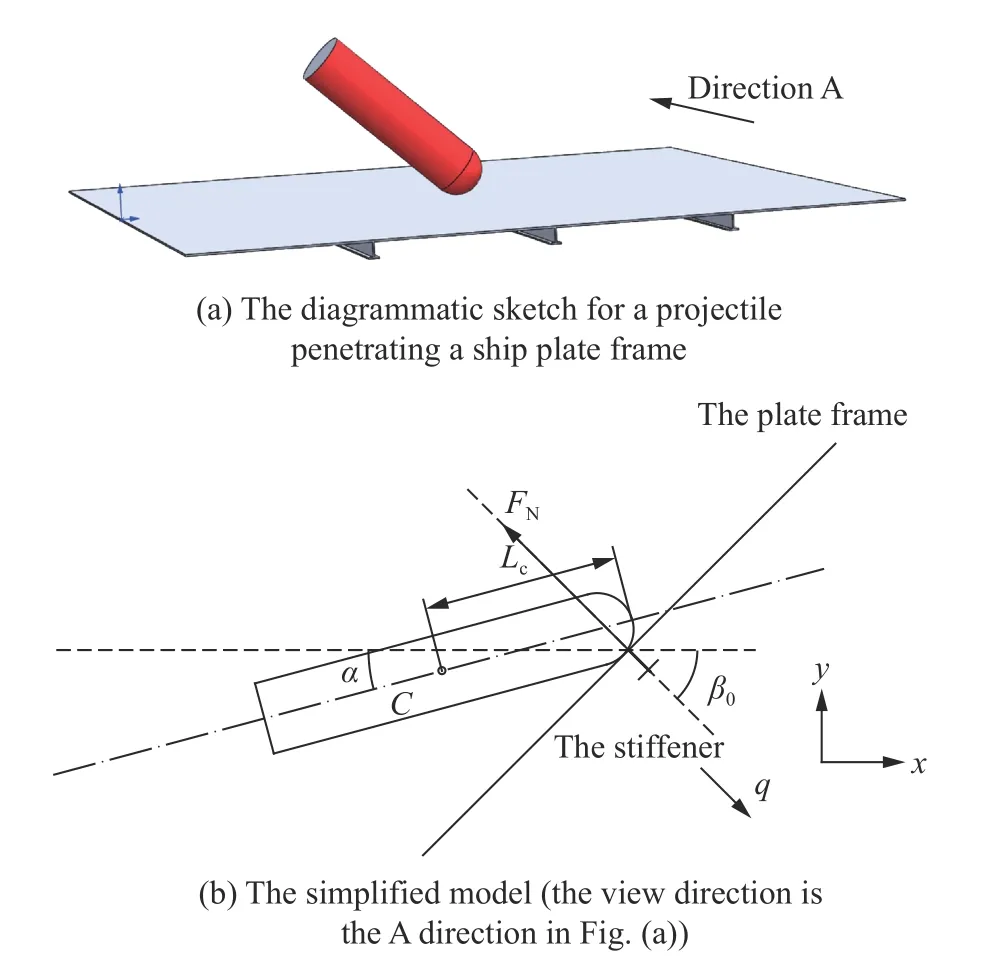
图2 弹体侵彻板架结构示意图与简化模型Fig.2 The diagrammatic sketch and simplified model for a projectile penetrating a ship plate frame

1.1 弹体运动方程

在侵彻过程中，由于加强筋的位移相比靶面尺寸是微小的，因此假设侵彻过程中靶面角度不变，而弹头受力FN沿靶面法线方向。加强筋受力大小为FN，方向与弹体受力反向。定义靶面法线方向为q方向，如图2所示，加强筋中点沿q方向位移为w。加强筋运动局部坐标系如图3所示。在弹体作用下，加强筋塑性铰不断向边界移动，塑性铰坐标为ξ。假设加强筋速度场为线性分布，如图3所示，沿全梁分布的速度场可表达为：

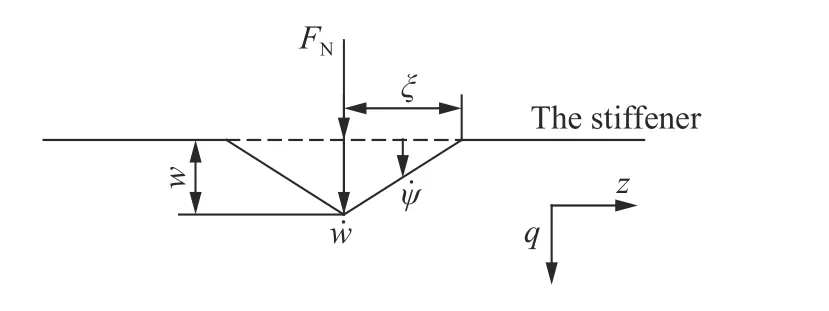
图3 加强筋运动速度场Fig.3 Velocity field of the stiffener

式中：Jc为弹体转动惯量。实际问题中，转角α 随时间而改变，即：

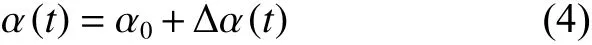
式中：Δα（t）为转角随时间变化量。由于侵彻时间较短，Δα（t）相比于β0+α0很小，因此式（4）简化为：

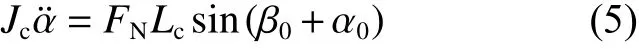
弹体质心C 垂直于靶面位移为Wc，平行于靶面位移为Uc，如图4所示。弹体沿q 方向运动方程为：

式中：m0为弹体质量。

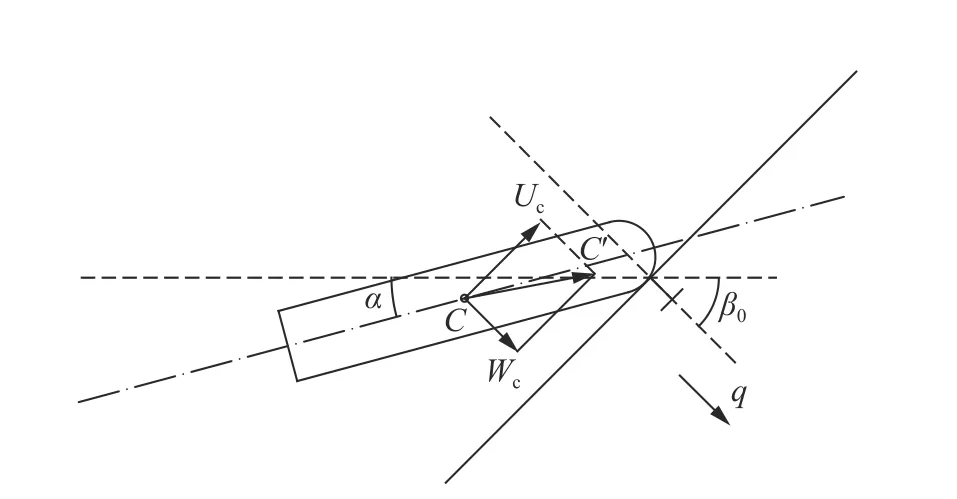
图4 弹体质心位移Fig.4 Displacement of the mass center of the projectile

1.2 加强筋运动方程与塑性铰移动

由刚体运动可知，弹体质心位移Wc与梁中点挠度w 的关系为：

由式（6）和（7）可得：

进一步将式（8）代入式（3），可得：

式中：m 为等效质量。m的表的式为：

假设侵彻过程中，弹体在平行于靶板方向不受力，因此平行于靶板的速度分量U˙c保持不变：

由梁的受力平衡方程可得：

式中：m为梁的单位长度质量。代入式（9）可得：

在塑性铰处，仅有梁的极限弯矩M0作用，而没有剪力，因此由弯矩平衡方程可得：

对式（13）～（14）进行求解，可得梁挠度公式。文献[12]中对求解过程有详细论述，本文不做赘述，仅引用其结论。梁变形区域挠度公式为：

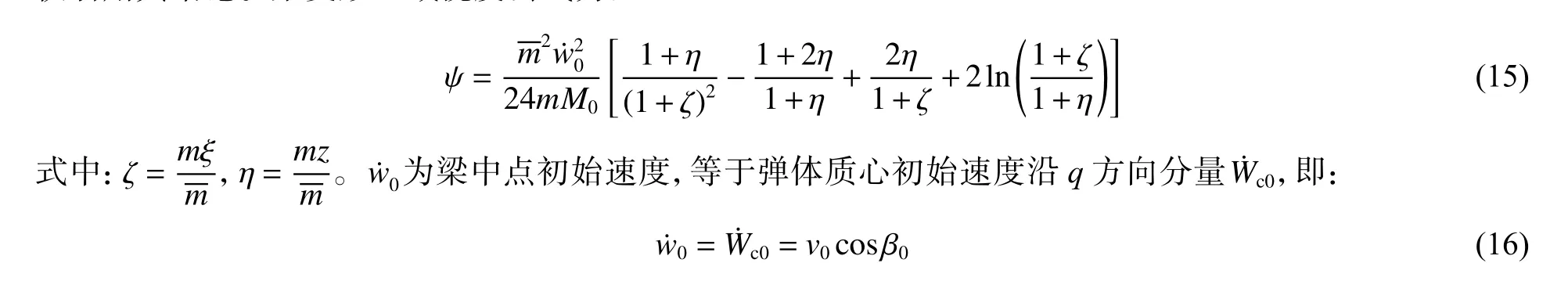
对于图3所示梁的运动，梁的塑性应变可表示为：

随着中点位移增大，塑性应变增加，直到塑性应变达到断裂应变εm，梁破坏，侵彻过程结束。利用式（17）可得梁破坏的条件为：

利用式（15）、（18），可得到梁破坏时的塑性铰坐标ξm满足的方程：

1.3 侵彻结束后弹体剩余速度与姿态角求解

w˙ 与ξ 之间存在关系式：

利用式（20），在得到ξm后，即可求出梁破坏时的中点速度w˙m。

由文献[12]，侵彻过程中时间与塑性铰位置关系为：

利用式（21）即可得到梁发生破坏的时间tm。由于梁发生破坏之后，其对于弹体作用力会明显降低，因此本文认为梁出现破坏的时间tm即为侵彻受力结束时间。在tm时刻之后，弹体作自由运动。

下面求解tm时刻前的弹体运动。利用式（5）和（9），得到弹体转角α 的方程为：

对式（22）进行积分，并利用梁中点挠度和弹体转角初始条件：

可得弹体转角的解为：

式中：

侵彻结束时弹体转角αm为：

式中：wm为梁破坏时中点位移。

可见，弹体攻角和着角的变化与弹体初始速度、初始着角、初始攻角以及加筋板结构形式相关。

如图4所示，弹体初始质心为C 点，侵彻结束后质心为C′点，弹体质心在q-z 坐标系下的位移为：

式中：Wcm和Ucm分别为弹体质心沿q 和z 方向位移，∆ αm为侵彻结束时转角改变量。

弹体的剩余速度为：

式中：W˙cm为侵彻结束时弹体质心沿q方向速度。

弹体质心C 水平与垂直方向位移分别为：

式中，Ucx和 Ucy分别为弹体质心水平和垂直方向位移。

下面求解弹体着角改变量。图5为侵彻结束后弹体质心速度，其垂直靶面速度为W˙cm，平行靶面速度为U˙c不变，侵彻结束后，合速度方向会产生Δβm的改变，Δβm即弹体着角改变量，其计算公式为：

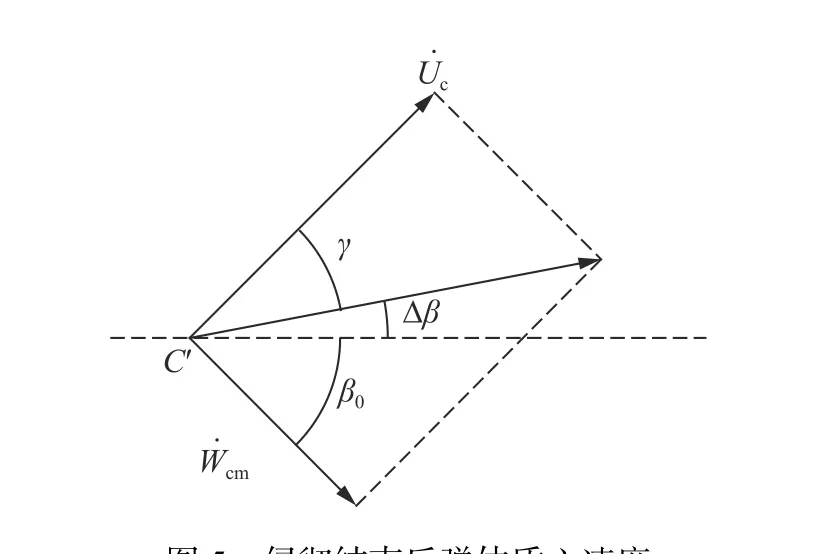
图5 侵彻结束后弹体质心速度Fig.5 Centroid velocity of the projectile after penetration

此时求解出的Δβm和Δφ为侵彻结束时的着角与攻角改变量。

弹体出靶到飞行至下一层甲板过程中，其运动为自由刚体运动。由于弹体不再受力，因此着角不变，飞行至下一甲板时，着角为：

而弹体在飞行过程中，会以α˙m的角速度旋转，因此抵达下一层靶板时，攻角为：

式中：H 为甲板间距。

根据以上公式，可以求解弹体侵彻板架结构攻角和着角的变化量。

2 理论公式的数值验证

本节通过数值方法，对弹体侵彻舰船加筋板结构转角变化理论公式进行数值验证。

2.1 典型计算模型的选取

以某7 000吨级目标舰船的船舯区域第1层甲板作为板架结构数值模型，板架结构尺寸为20 m×15 m，板架结构材料为921A 钢，材料模型采用Cowper-Symonds模型，材料参数见表1，板架结构具体结构参数如表2所示。弹体质量为300 kg，长度为1 200 mm，头部到弹体质心的距离为600 mm，转动惯量为34.77 kg·m2，弹体材料为30CrMnSiNi2A，材料参数见表1。根据以上参数在ANSYS有限元建模软件中对弹体和靶板进行建模并网格划分，为了提高计算效率，对于甲板板架模型的网格局部进行网格细化，弹着点附近网格大小取为0.02 m，网格沿着弹着点向周边扩散，在边界处网格大小为0.1 m。通过Hypermesh 网格处理软件调整弹体着角和攻角的大小以及调整弹体和靶板的位置，使弹着点位置为板架结构横梁处。采用LS-DYNA 有限元软件的Lagrange算法进行数值计算，拉格朗日坐标下使用的网格离散算法，能够直观地提高物体变形的折弯模式，适用于大变形和大转动的情况。

表1 板架结构与弹体材料参数Table 1 Material parametersof the plateframe and the projectile

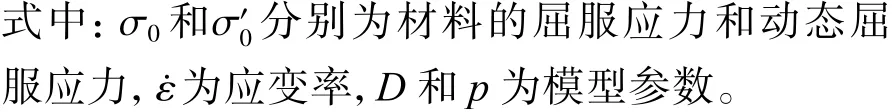
2.2 弹体剩余速度理论与数值结果的比对

基于上节推导的理论公式，通过Matlab编写程序代入板架结构和弹体参数计算。求解出不同输入条件下弹体侵彻结束后的剩余速度，并与LS-DYNA 有限元软件数值求解的结果进行比对，计算结果如表3所示。

通过比较分析，对于弹体在高速侵彻板架的过程中，本文推导得出的弹体剩余速度预测公式与数值计算结果较为接近，两者速度降误差在20%以内。

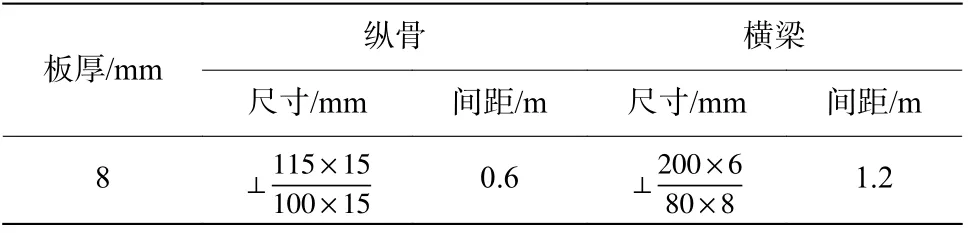
表2 板架结构参数表Table2 Structural parametersof the plate frame

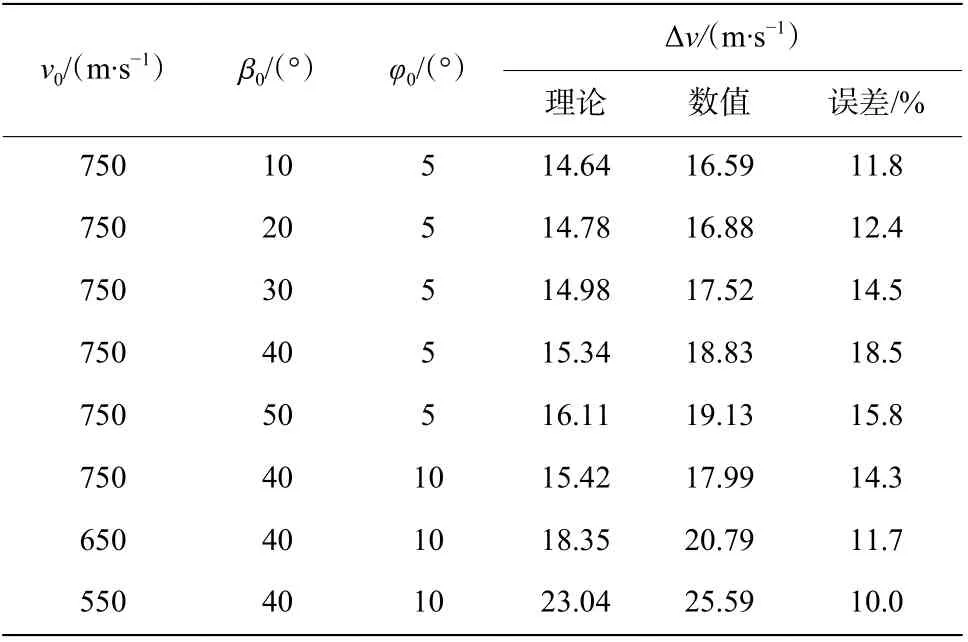
表3 数值与理论剩余速度结果比对Table3 Comparison of the numerical and theoretical results of theresidual velocity

2.3 弹体转角变化理论与数值结果的比对

本节针对弹体侵彻过程中的转角计算公式的可行性进行数值验证。本文中选取弹体的着角为10°～50°，选取弹体的攻角为5°～10°，弹体初始速度为450～750 m/s。在LS-DYNA进行侵彻计算时，对于着角的计算，本文中通过提取质心在x、y、z 这3个方向上的速度，通过反三角函数变换进行求解；对于攻角的计算，在本文中通过在软件中提取弹体轴线首尾两端端点坐标，通过反三角函数变化可解出弹体在侵彻过程中转角的大小，通过转角减去弹体的着角则可得到当前时间弹体的攻角大小。具体理论公式求解结果与数值计算结果如表4～5所示。

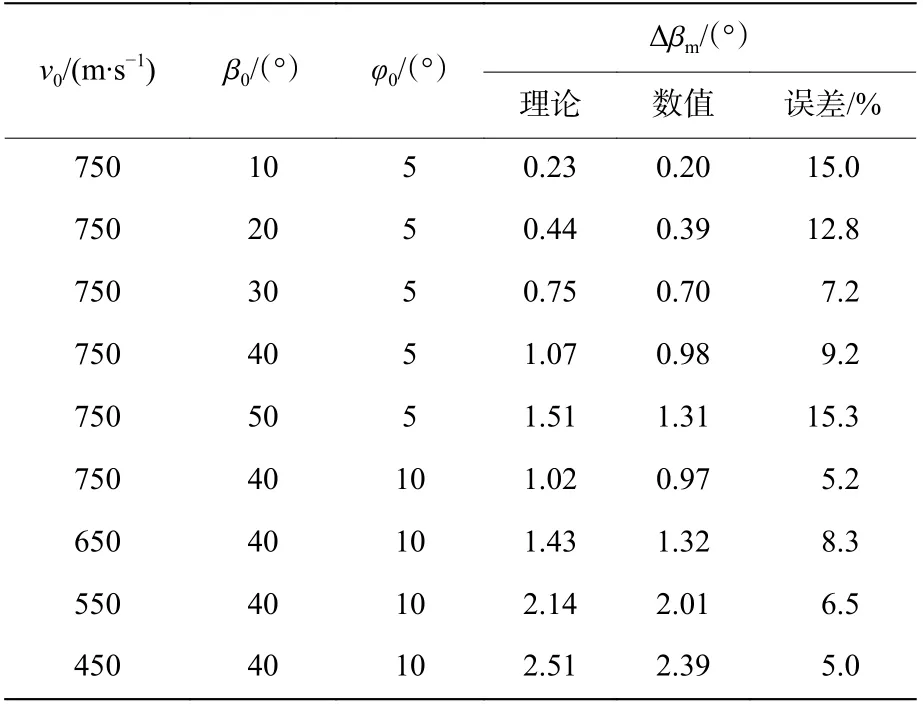
表4 数值与理论着角结果比对Table 4 Comparison of the numerical and theoretical results of the impact angle

表5 数值与理论攻角结果比对Table 5 Comparison of the numerical and theoretical results of the attack angle

可以看出，在弹体高速侵彻下，着角与攻角预测公式理论结果与数值结果的误差较小，弹体出靶时刻的着角和攻角误差均在15%以内。

3 实 验

本文中理论模型是针对反舰导弹侵彻舰船板架结构提出的，假设弹体质量大、速度高，且板架结构为舰船板架。对于此类实验报道较少，而有关弹体转角变化的文献则更为稀少。文献[13]报道了类似实验，且测量了弹体转角变化，因此，针对文献[13]中的实验工况对理论和实验结果加以对比。

该实验中弹体长度为1 200 mm，直径为250 mm，弹体设计着靶速度为750 m/s，初始着角为40°，初始攻角为2.8°。靶标为4层，如图6所示，其中第1、3、4层为船用907A 钢，第2层为船用921A 钢。各层靶板参数如表6所示。文献[13]对目标舰船靶标火箭橇实验进行了分析，给出了弹体剩余速度、姿态角等测量值。该实验通过高速摄像系统对弹体和靶标系统进行动态捕捉，将捕捉的图像结果进行数据测量得到弹体与靶标系统的相关实验数据。

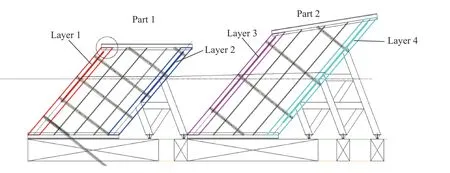
图6 实验靶标示意图[13]Fig.6 Schematic diagram of the experimental target[13]

实验中每层靶板出靶剩余速度和弹体着靶姿态角结果如表7所示，本文中理论计算的相应数据也见表7。此处姿态角为攻角与着角之和，因为实验通过高速摄像分析弹体姿态，无法区分攻角和着角分别为多少度，因此只给出了姿态角数值。由于实验过程中产生大量的火光，导致弹体穿透第1层靶板至第2层靶板间无法清晰观测，因此表7中第1层出靶剩余速度和第1层着靶姿态角数据缺失。

从表7中可以看出，随着侵彻层数的增加，姿态角理论预测结果与实验结果的误差越来越大，这是由于每层预报误差累积的结果。对于实验4层靶标，姿态角预报最大误差在15%以内。剩余速度理论预测结果与实验结果差别较小，误差在3%以内。虽然实验弹头形状不是球头弹，而是卵型弹，但姿态角最大误差在15%以内，由此可见本文中的理论方法具有一定工程预测价值。

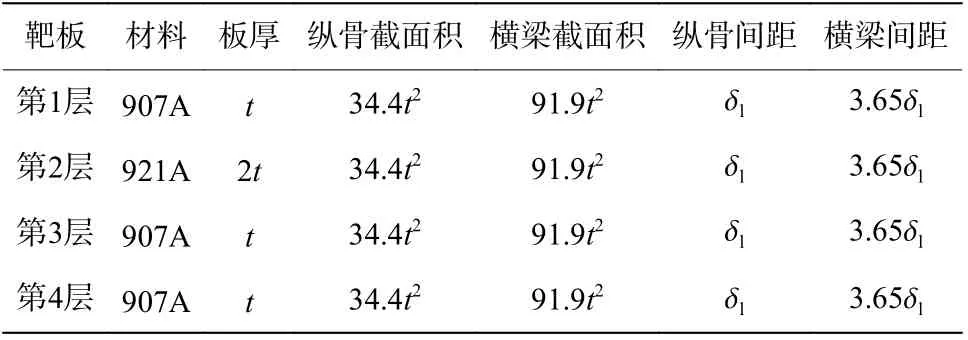
表6 靶标板架结构参数[13]Table 6 Structural parameters of the target frame[13]

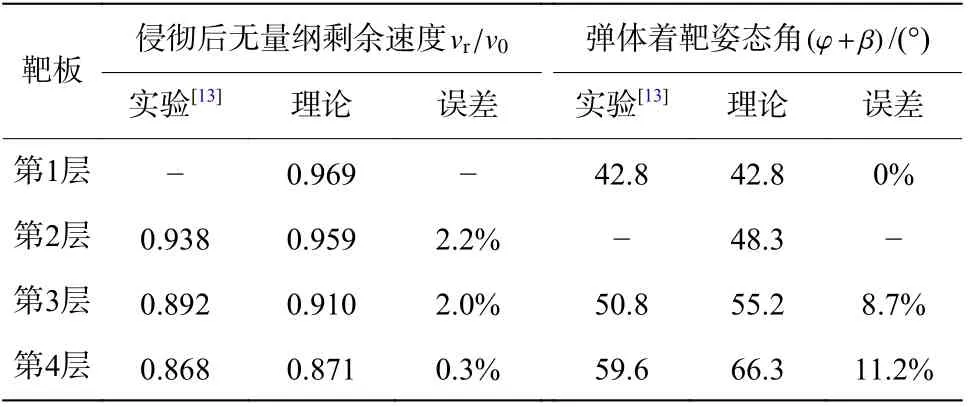
表7 试验与理论结果比对Table 7 Comparison of experimental and theoretical results

4 弹体姿态角变化影响参数分析

本节基于前文推导的弹体侵彻姿态角理论计算方法，分析不同参数对姿态角变化的影响。

4.1 侵彻过程中转角变化规律

首先分析侵彻过程中转角变化Δα。对于β0=40°，v0=750 m/s，α0分别为−10°、0°、10°和20°的情况，图7是计算得到的侵彻过程中Δα 曲线。弹体姿态角增加量Δα 随时间的增加不是线性的，而是随着时间的推移，增加速率会变大。这通过式（25）可以看出，Δα 随时间的变化由斜率为Av0cosβ0的线性项和−AΔw 组成，侵彻开始时，梁中点挠度w 变化速率较快，随着时间的推移，w 变化速率下降，因此Δα 变化速率增加，且Δα 曲线斜率趋向于Av0cosβ0。初始攻角α0越大，则Δα 增加越快。图中曲线在约0.24 ms 时截断，这时梁已经破坏，按本文假设，侵彻结束。

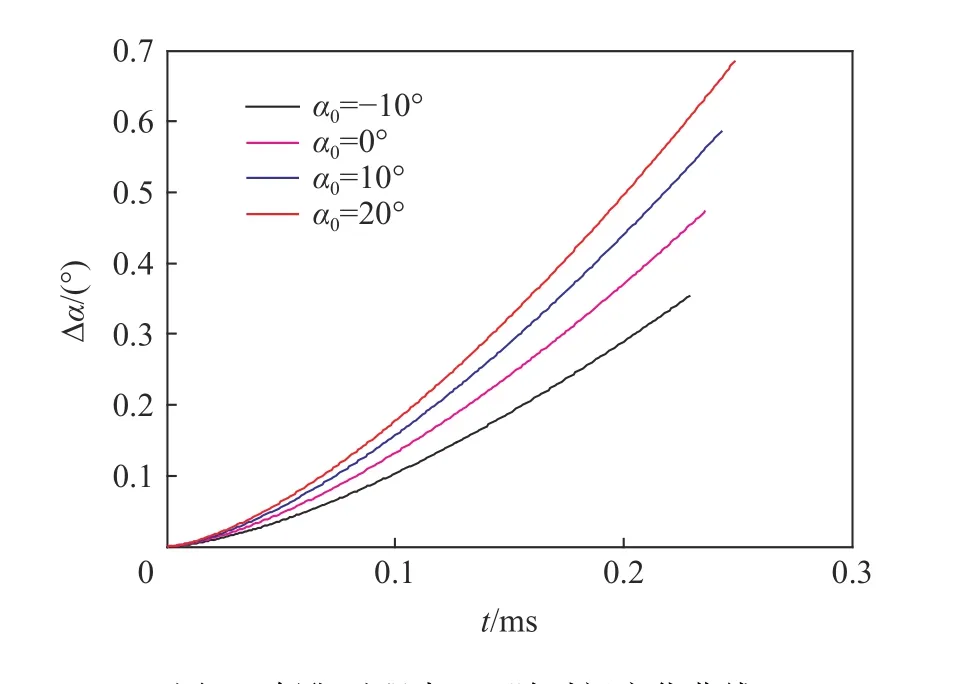
图7 侵彻过程中Δα 随时间变化曲线Fig.7 Timevarying curves of Δα in the penetration process

4.2 初始攻角对转角变化的影响

下面分析侵彻结束后转角改变量Δαm与初始攻角的关系，针对着角分别为10°、20°、30°和40°情况，计算值见图8。Δαm随着初始攻角和着角的增加而增加，而着角对于Δαm的影响大于初始攻角。以40°着角侵彻为例，初始攻角每增大1°，Δαm增大约0.01°，而着角增大1°，Δαm增大约0.04°。对于图9中的着角变化，则着角改变Δβm随初始攻角变化十分不明显，只与初始着角相关较大。

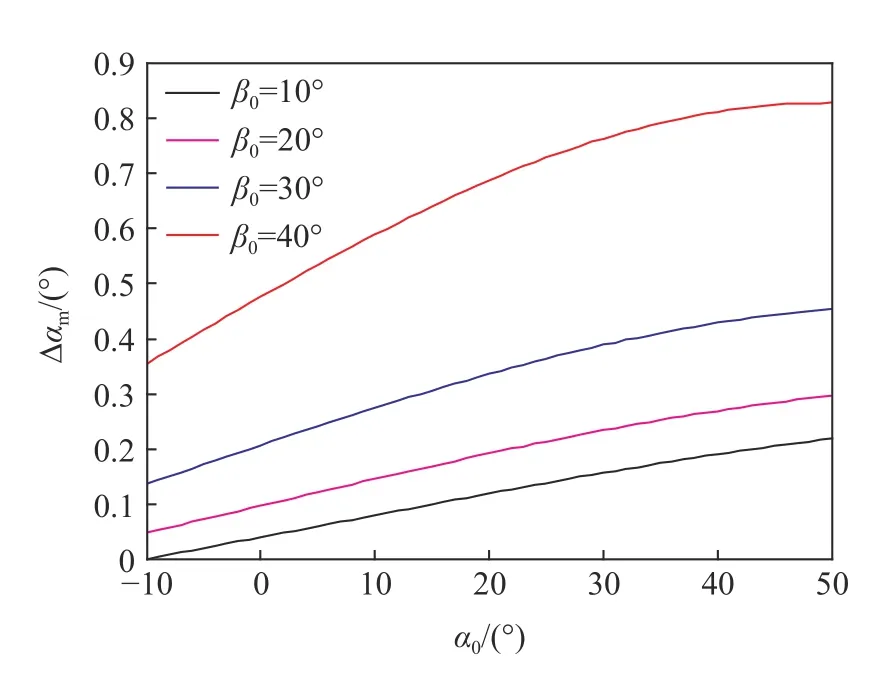
图8 侵彻结束时转角改变Δαm 与初始攻角的关系Fig.8 Relationship between the change of rotation angle and the initial attack angle

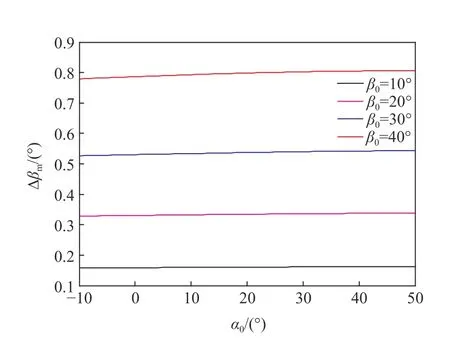
图9 侵彻结束时着角改变Δβm 与初始攻角的关系Fig.9 Relationship between the change of impact angle and the initial attack angle

飞行至下一层甲板时的攻角变化Δφ见图10，可见，攻角和着角对于Δφ影响都较大，而着角的影响大于初始攻角。在小着角、小攻角入射情况下，Δφ值可能较小，即飞行至下层甲板时攻角变化小。但在大攻角、大着角情况下，Δφ 值可能很大。以40°着角为例，即使0°攻角入射，飞行至下层甲板时攻角改变也达到约10°。这说明加强筋对于弹体攻角会有较大改变作用。

剩余速度随攻角变化见图11。由图11可见，初始攻角和着角对于剩余速度的影响极小，图中变化不足1 m/s。

4.3 初始着角对转角变化的影响

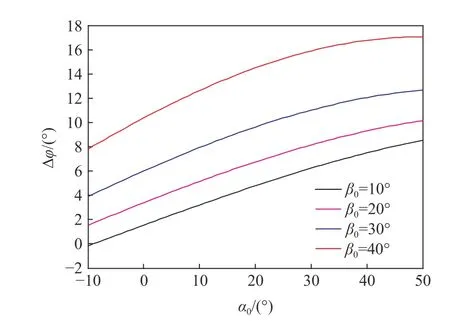
图10 飞行至下层甲板时攻角变化Δφ与初始攻角的关系Fig.10 Relationship between the change of attack angle Δφ at the next deck and the initial attack angle

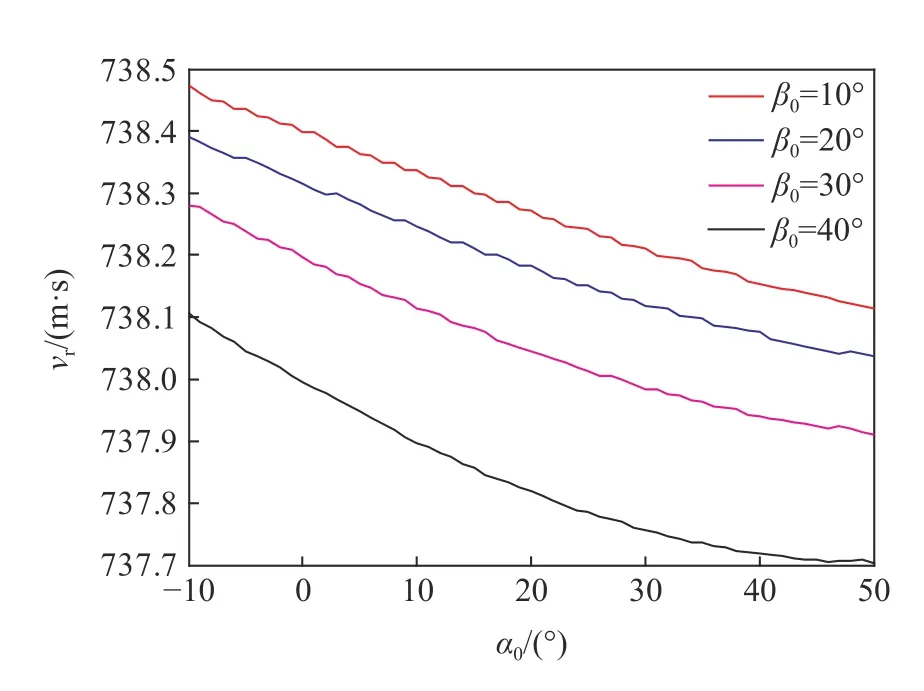
图11 剩余速度随初始攻角变化图Fig.11 Residual velocity versus initial attack angle

进一步分析初始着角的影响。由图12、13可见，攻角随着初始着角的增加而增加。由各个初始攻角的曲线十分接近，进一步看出，对于攻角变化而言，初始攻角的影响小于初始着角的影响。初始着角在40°之前，其对攻角变化影响较小，而在40°之后，攻角改变迅速增加，并在某个着角处曲线截断。曲线截断的原因是弹体不能穿透梁，即产生跳飞，而图中曲线截断的着角即本文中理论模型预测的跳飞着角，在约65°。在大于40°的着角情况下，弹体侵彻后偏转都会达到5°～25°，飞行至下层甲板时攻角达到30°以上，这对于弹体侵彻是十分不利的。因此，实战中要避免着角过大。

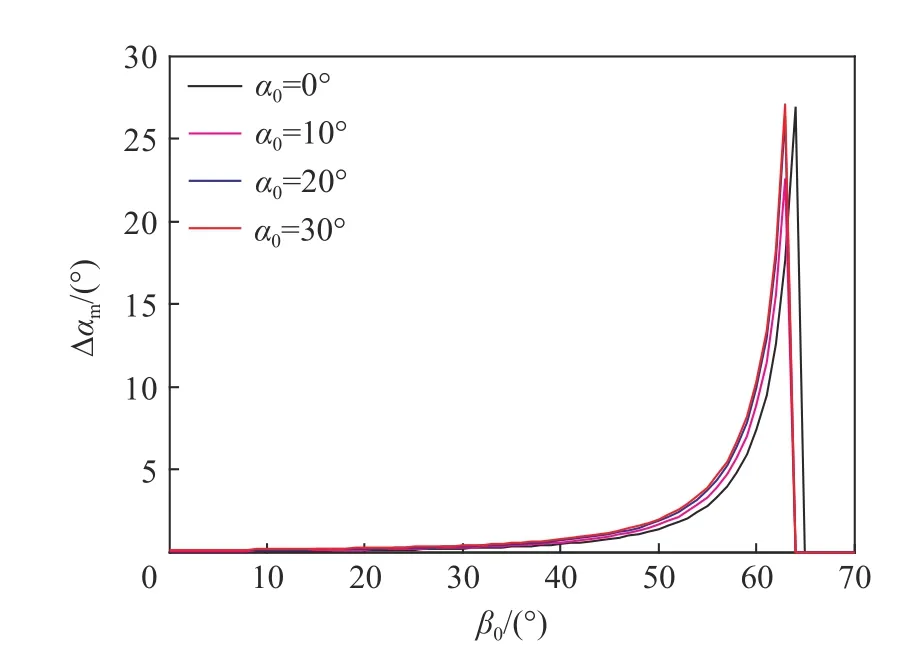
图12 侵彻结束时转角改变Δαm 与初始着角的关系Fig.12 Relationship between thechange of rotation angleand theinitial impact angle

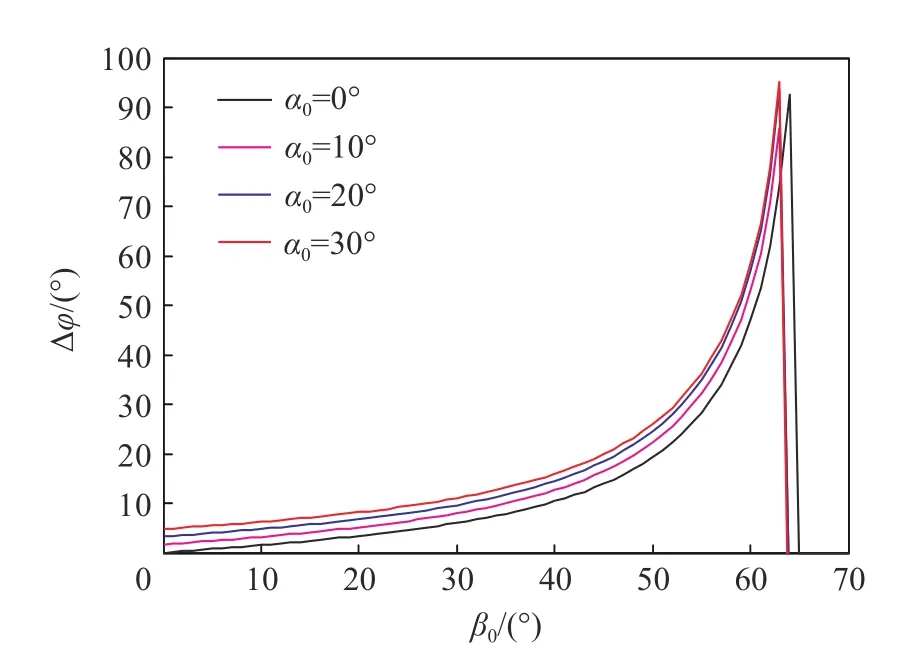
图13 飞行至下层甲板时攻角变化Δφ与初始着角的关系Fig.13 Relationship between thechangeof attack angleΔφ at the next deck and the initial impact angle

4.4 初始速度对转角变化的影响

下面考察初始速度的影响，假设初始攻角为2°，初始着角分别为10°、20°、30°和40°。结果如图14～15所示，可以看出初始速度低于某一值时，曲线截断，这个值是本文理论模型预测的极限速度。在超过极限速度情况下，速度越低，则弹体偏转约严重，着角改变也越大，因此高速侵彻可以降低着角和攻角的改变。

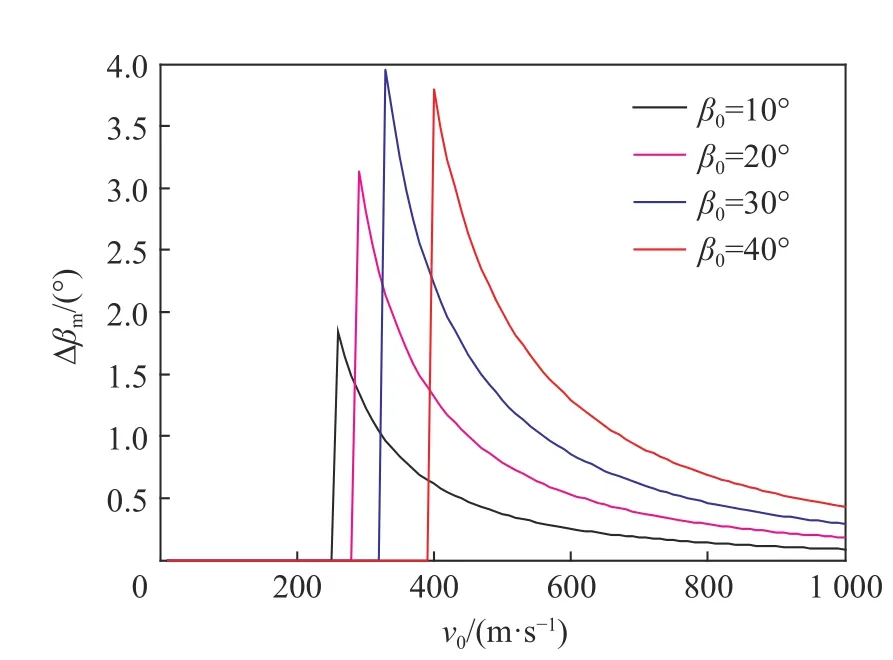
图14 初始速度对着角改变的影响Fig.14 The influence of initial velocity on the change of impact angle

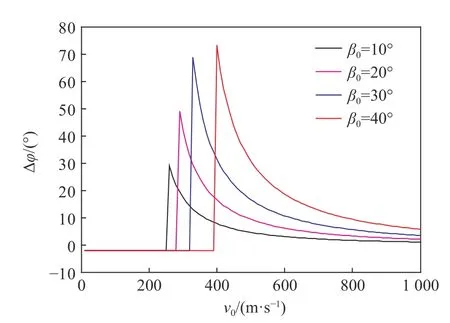
图15 初始速度对飞行至下层甲板时攻角变化Δφ的影响Fig.15 Theinfluence of initial velocity on the change of attack angle Δφat the next deck

4.5 板架结构形式对转角变化的影响

下面对结构进行考察，假设初始攻角为2°，初始着角分别为10°、20°、30°和40°。结果如图16所示，可以看出随着极限弯矩M0的增大，弹体偏转越发严重，这是直观的现象。且攻角改变量Δφ随着M0的增大近似线性增大，由图中数值可知，M0增大一倍，Δφ增大也近一倍。

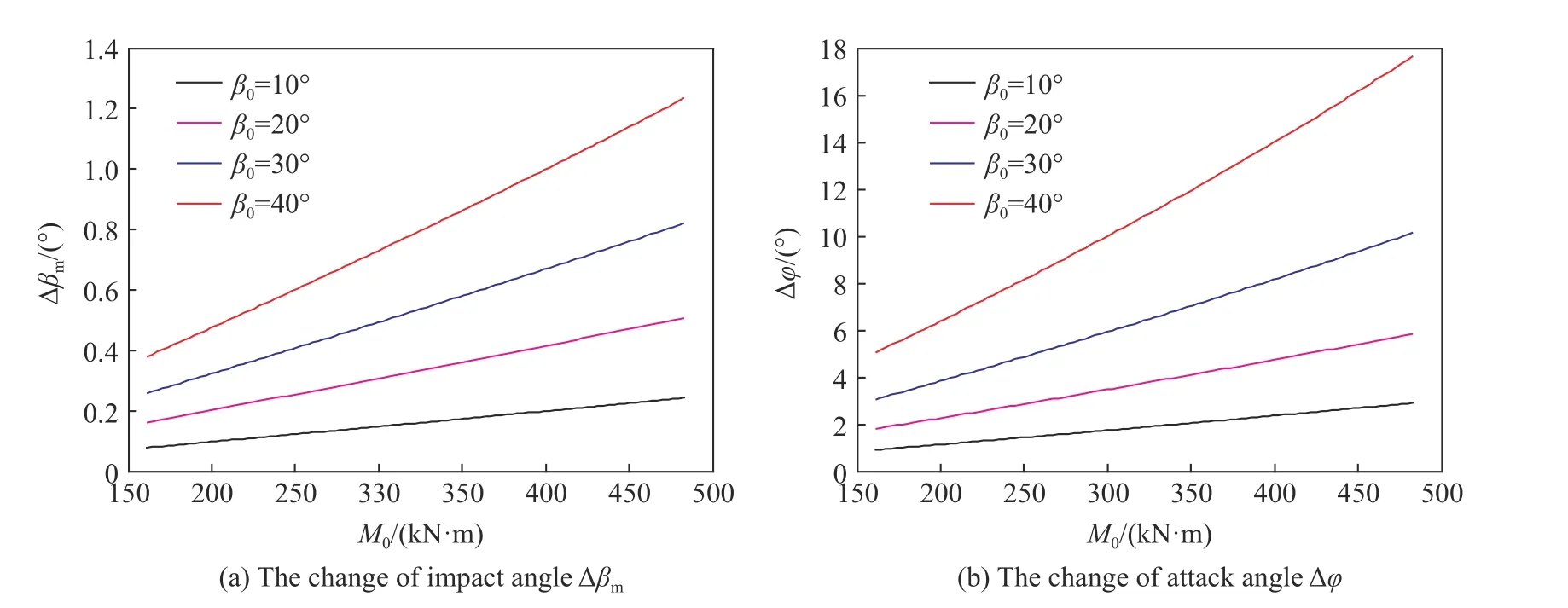
图16 梁的极限弯矩M0对着角和攻角改变的影响Fig.16 The influence of the ultimate moment of the beam on the changes of impact angle and attack angle

5 结 论

针对刚性球头弹体侵彻舰船板架结构加强筋问题开展理论研究，主要结论如下：

（1）将加强筋简化为刚塑性梁模型，建立了侵彻过程力学模型，给出了弹体剩余速度、着角和攻角变化的求解公式，发现弹体攻角和着角的变化与弹体初始速度、初始着角、初始攻角以及加强筋极限弯矩有关。通过实船板架结构侵彻数值计算佐证了理论模型的有效性。

（2）通过理论公式计算并分析了各种侵彻参数对于侵彻剩余速度、着角和攻角变化的影响，发现理论公式可以给出极限速度、跳弹参数的预报。

（3）弹体侵彻结束后攻角的变化量与初始攻角和着角有关，其中初始着角影响较大；着角的变化量受初始攻角影响极小。侵彻初始速度越高，则弹体侵彻结束着角和攻角变化越小。弹体侵彻剩余速度受初始攻角和着角的影响很小。

（4）初始着角对于侵彻攻角变化的影响存在两个典型拐点，着角超过第1个着角拐点（本文算例对应的着角为40°），则攻角改变会急剧增大；着角超过第2个拐点（本文算例约65°），弹体发生跳飞。

（5）加强筋的极限弯矩对弹体攻角改变有较大影响，极限弯矩增大一倍，攻角变化量也增大近一倍。