基于迂回相位和几何相位复合的散射调控超表面

张忠涛， 王甲富， 翟伊鹏， 楚遵天， 贾宇翔， 朱瑞超

(空军工程大学基础部，西安，710051)

超材料是一种由亚波长单元组成的人工周期结构[1-4]。超表面则是超材料的二维形式，可以减小超材料的体积，便于器件的微型化设计。超表面在电磁散射调控方面具有很好的灵活性，如极化转换、涡旋波束生成、电磁波束偏转和分裂等[5-10]。目前，许多成功的散射调控超表面被提出[11-16]。文献[17]给出了一个相位调制超表面，通过引入传输相位作为附加自由度，使同极化和交叉极化散射波具备不同的功能。文献[18]提出了一种利用传输相位来实现可编程全息的编码超表面。文献[19]提出了一种全空间多功能超表面，其几何相位设计使得散射波束发生偏转，传输相位设计使电磁波透射并产生涡旋波。上述研究成果大多是基于传输相位和几何相位，且仅针对电磁波垂直入射的情况。一般来说，当入射电磁波斜入射时，特别是大角度入射时，由于阻抗失配，超表面对电磁波的调控性能会变差。因此，人们迫切地需要一种能够有效控制斜入射电磁波的方法。

近年来，许多基于异常光学衍射(extraordinary optical diffraction, EOD)的超表面被提出[20-22]。如文献[23]将频率无关的几何相位和迂回相位无缝结合设计了一种EOD多自由度超表面，实现了可见光下的彩色全息图。研究表明，迂回相位本质上独立于入射角和波长，它为调控斜入射电磁波提供了一个很好的方法。迂回相位无需改变结构参数或改变结构单元的空间取向，仅通过超表面结构单元在晶格内的位错即可引入。但是，迂回相位作用于衍射波束，需要先根据EOD理论将入射电磁波高效地引入至衍射通道，然后通过移动结构单元引入迂回相位，进而实现对斜入射电磁波的有效调控。

本文提出了一种基于迂回相位和几何相位复合的电磁散射调控超表面设计方法，以实现不同入射角下对电磁波的独立调控。作为设计实例，采用能够实现宽带极化转换的开口谐振环(split ring resonator, SRR)作为超表面结构单元，通过移动和旋转SRR同时引入迂回相位和几何相位。当电磁波垂直入射到超表面时，几何相位设计使得散射波分裂为两束；斜入射时，大部分散射波被引导至-1阶衍射通道，通过迂回相位设计实现了波束偏折功能。仿真和测试结果均验证了其良好的散射波束调控性能。该设计方法丰富了超表面操纵电磁波的自由度，并可进一步与传输相位、共振相位等复合推广到全空间散射波束调控超表面设计。

图1 利用迂回相位和几何相位的超表面示意图

1 理论与设计

图2为迂回相位示意图。以-1衍射级为例阐述迂回相位的产生原理。根据EOD理论，理想情况下，入射电磁波可以衍射到-1衍射级。如图2(a)所示，在移动结构单元之前，相邻的结构单元在衍射方向上具有相同的相位差。也就是说，对于均匀的周期分布排列，相邻结构单元之间的相位差始终为零。但是，如图2(b)所示，将一个结构单元从原始的周期晶格中移动出来后，相邻结构单元之间的相位差将产生差异，这种差异就是迂回相位。

(a)位移之前的光路

1.1 迂回相位的理论分析

由于迂回相位存在于衍射波束中，如果衍射波束幅值很小，则很难观测到迂回相位。所以，我们需要将入射电磁波尽可能地引入至某一个衍射通道。各衍射级的生成条件如图3所示，该衍射级图由许多Wood’s Anomaly (WA)线组成。

图3 k-空间衍射阶图

WA线由式(1)表示[24-25]:

(1)

式中：kx为平行波矢；k0为整体波矢；p0为超表面的周期；m为衍射级数。平行波矢kx=k0sinθ0，整体波矢k0=2π/λ，其中θ0为入射角，λ为波长。可以发现，k0总是在第0级WA线以上，所以第0衍射级总是存在；而当k0超过-1阶WA线时，-1衍射级就开始出现。其他衍射阶的产生同理可得。

为了将入射电磁波转移至可控的衍射阶，我们选择将kx和k0放在图3的绿色区域。这意味着只有第0阶和-1阶衍射可以存在。换句话说，kx和k0应该被第0、第1、第-1和第-2 WA线包围。根据衍射级图，应满足以下条件:

(2)

此外，对于具有周期性p0的超表面，绿色区域的-1阶衍射方程为:

(3)

式中：θ-1为第-1阶衍射角。因此，当入射电磁波满足上述方程(2)和(3)时，-1衍射阶的幅值会增大。

接下来我们进一步分析迂回相位产生的原因。图2(a)是均匀的周期分布排列。当电磁波入射到相邻2个单元时，反射波将提供一个与电磁波传播路径相关的相位[26]:

Δφ=k0(dm-d0)

(4)

这里，选择-1衍射阶(m=-1)。同时，入射波矢和衍射波矢的平行分量为：

k0x=k0sinθ0,k-1x=k0sin(-θ-1)

(5)

它们有相反的符号。因此，方程式(4)改写成：

Δφ=k0(d-1+d0)=k0p0(sinθ-1+sinθ0)

(6)

式中：d0和d-1表示入射和衍射方向上对应的光程差。将式(3)代入式(6)可得：

Δφ=k0p0(sinθ-1+sinθ0)=2π

(7)

这说明对于均匀周期分布的排列，相邻结构单元之间的相位差是相同的。

但是，如图2(b)所示，将一个结构单元从原来的周期晶格中移动出来后，电磁波的传播路径会发生改变，相邻结构单元之间的相位也会不同，相位差为:

Δφ′=k0(d-1′+d0′)=k0px(sinθ-1+sinθ0)

(8)

式中：px表示移动后的晶格距离。将式(3)代入式(8)，可以得到:

(9)

式(9)就是通过移动结构单元引入的迂回相位。由公式可以看出，迂回相位只与结构单元的相对位置有关，而与频率、极化和入射角无关。只需连续改变结构单元的位移，就可以连续地将迂回相位从0调整到2π。

1.2 结构单元设计

为了更好地表现迂回相位对波束调控的效果，选择了一个特例来直观地显示电磁波进入-1衍射阶的效率。当入射角与衍射角一致时，入射电磁波会被逆反射回来。也就是说，电磁波进入-1衍射阶通道的效率可以直接通过逆反射的大小来表示。将θ-1=θ0代入式(3)，得到逆反射条件如下：

(10)

该式表明频率和逆反射角是相关的，两者都可由超表面的周期调控。作为一个设计实例，我们选择了频率为20.0 GHz、逆反射角为48.6°的情况。根据式(10)可以算出p0等于10 mm。

本文采用一个可以实现宽带极化转换的SRR作为结构单元。值得一提的是，尽管当电磁波的条件满足式(2)和式(3)时，仍会有部分电磁波进入0阶衍射通道。因此，为了提高-1阶衍射效率，可以通过改变结构参数来抑制0阶衍射。

最终的结构单元如图4(a)所示。顶部SRR和金属背板的厚度均为0.018 mm，电导率为5.8×107S/m。它们之间有一层3 mm厚的F4B介质层(介电常数2.65，损耗角正切0.001)。其他参数分别为p=10 mm,l=6 mm,w=0.3 mm,g=0.42 mm,a=4.44 mm。利用CST Microwave Studio的频域求解器对其进行数值仿真。仿真过程中，将结构单元的x、y方向设置为周期边界条件，z方向设置为开放边界条件。极化转换的性质通过反射系数来研究。rxx(ryy)为x(y)极化电磁波下的同极化反射率，ryx(rxy)为x(y)极化电磁波下的交叉极化反射率。从图4(b)可以看出，在9.70～16.25 GHz内的x极化波和y极化波可以实现高效的交叉极化转换。我们将该结构单元命名为SRR0，并将旋转90°的相同结构单元命名为SRR1。对应的幅值和相位仿真如图4(c)所示。可以发现，它们的反射振幅rxy几乎不变，Δφ在宽带内约为180°。因此，可以通过旋转SRR来建立一个1-bit的反射单元。

(a)结构单元示意图

2 超表面仿真结果

接下来，将36×30个上述结构单元按照图5(a)排列。为了验证逆反射的效果，利用CST Microwave Studio中的时域求解器对其进行了数值仿真。数值仿真的示意图如图5(b)所示。在仿真过程中，将超表面倾斜θ°，从而使沿z轴的电磁波能够以θ°入射到超表面。仿真过程中，超表面的x、y、z方向均设置为开放边界条件。由于超表面的旋转对称性，只给出了20.0 GHz时θ=48.6°下的三维散射图。图5(c)和图5(d)表明TE电磁波和TM电磁波都可以实现逆反射，也就是说电磁波成功地进入了-1阶衍射通道。同时，为了便于观察逆反射效果，在相同的仿真条件下，采用相同尺寸的金属板作为对比。图5(e)和图5(f)为沿着xoz面的RCS，其中红线表示金属板，蓝线表示超表面。当电磁波以θ=0°入射至金属板时，反射波将在θ=97.2°处反射。当电磁波以θ=0°入射至超表面时，大部分反射波将在θ=0°处被反射回来。与金属平板相比，超表面在θ=0°处的反射率提高了约30 dBm2。因此，超表面取得了很好的逆反射效果。除此之外，本文还给出了TE电磁波和TM电磁波作用下的沿着yoz面的RCS。如图5(g)和图5(h)所示，可以看出在引入迂回相位之前，逆反射波束在y方向没有发生偏转。

图5 位移之前的超表面仿真结果

接下来，根据式(9)，移动结构单元可以引入迂回相位。作为一个功能性验证，利用迂回相位来实现-1阶衍射波束的y方向偏折。将在y方向排列的10个结构单元排成一组，然后依次向右移动1 mm以获得360°的相位覆盖。由于SRR发生了错位，所以错位后的超表面最终尺寸为370 mm×300 mm，略大于上述逆反射超表面。在y方向上的偏转角θry可以用下面的广义Snell定律来预测:

(11)

式中：L为总长度，L=100 mm。在20.0 GHz时，计算出θry为8.63°。图6为超表面在不同电磁波条件下的仿真结果。图6(a)和图6(b)为TE和TM电磁波以48.6°入射的仿真结果，可以看出反射后的衍射波束向+y方向发生偏折。图6(c)和图6(d)为TE和TM电磁波以-48.6°入射的仿真结果，可以看出反射后的衍射波束向-y方向发生偏转。此外，为了验证在y方向上的偏转角，给出了其在yoz平面上的RCS。在20.0 GHz时，图6(e)～(f)和图5(g)～(h)的偏转角度分别为8.6°和-8.6°，与理论计算结果一致。

图6 位移之后的超表面仿真结果

另一方面，由于几何相位设计，在极化转换带宽内正入射的电磁波将沿xoz面分裂为2束对称波束。根据式(11)可计算出，当频率为10.4 GHz时，θrx为46.1°；当频率为14.0 GHz时，θrx为32.4°。接下来，对x和y极化波作用下沿xoz面的RCS进行仿真，结果如图7(a)～(d)所示。可以发现，在10.4 GHz时分裂角度约为46.0°，在14.0 GHz时分裂角度约为32.0°，与理论预测基本一致。此外，为了评估波束分裂的带宽，图7(e)～(f)为9.0～17.0 GHz沿着xoz面的归一化散射密度图，黑色的虚线表示理论的分裂角度。从图7(e)～(f)可以看出，在9.7～15.7 GHz内，x极化和y极化波均可以实现良好的分束效果。

图7 位移之后的超表面垂直入射仿真结果

3 实验验证

为了验证上述仿真结果，使用印刷电路板(PCB)技术制备了一个如图8(a)所示的370 mm× 300 mm样品，图中的插图为结构单元的放大视图。实验装置如图8(b)所示。整个测试系统是在微波暗室中进行的，墙面上贴有吸波材料，以避免来自环境的不必要反射。在实验过程中，使用2个喇叭天线和一个安捷伦E8363B网络分析仪对样品进行测试。

首先对迂回相位的仿真结果进行实验验证。测试过程中，样品倾斜48.6°放置，测试平面为yoz平面。图8(c)和图8(d)分别为20.0 GHz、TE波和TM波作用下的远场反射率图。图8(c)表明主波束在yoz平面内偏折约-7.5°，图8(d)表明主波束在yoz平面内偏折约-8.0°。2种极化的测量结果均与仿真结果相近，表明迂回相位能有效地控制斜入射电磁波。

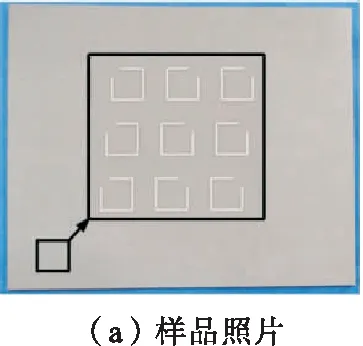
图8 实验装置及斜入射下的测试远场辐射图

其次对几何相位的仿真结果进行实验验证。图9为电磁波正入射时沿xoz面的测试结果。图8(a)和图8(b)给出了10.4 GHz时x和y极化波垂直入射的反射率图。两测试图表明电磁波在xoz面上被分裂到±47.0°和±45.0°的方向，这与图7(a)和图7(b)大致相同。同样，图9(c)和图9(d)给出了14.0 GHz时x和y极化波的反射率图，可以看出电磁波被分裂到±32.2°和±31.7°，与图7(c)和图7(d)基本一致。图7(e)～(f)为仿真和实测的归一化散射密度图，其中白色星号代表实测的最大散射角度。可以发现实测的数值与理论值有一些轻微的偏差。角度的微小偏差是由于试验环境的干扰和实验中样品放置的差异造成的。在误差允许的范围内，测量结果与仿真结果基本一致。总而言之，我们提出的基于迂回相位和几何相位复合的电磁散射调控超表面设计方法，能够实现不同入射角下对电磁波的独立调控。

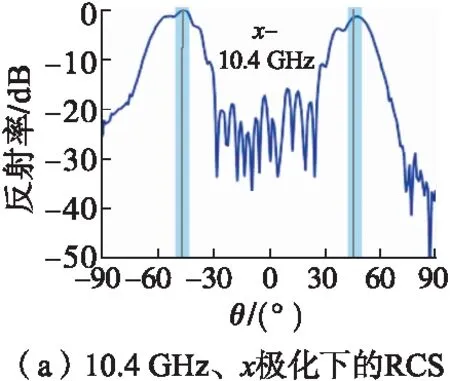
图9 位移之后的超表面垂直入射测试结果

4 结语

综上所述，我们提出一种利用迂回相位和几何相位来操纵不同斜入射电磁波的设计策略。通过旋转和移动结构单元分别引入迂回相位和几何相位。电磁波垂直入射至超表面时，散射波因几何相位设计而分裂。斜入射时，大部分散射波被引导至-1阶衍射通道，通过迂回相位设计实现了波束偏折。该设计方法丰富了超表面操纵电磁波的自由度，并可进一步与传输相位、共振相位等复合推广到全空间散射波束调控超表面设计。