基于TR技术的sin-FDA-MIMO距离角度联合估计

丁梓航， 谢军伟， 齐 铖

(空军工程大学防空反导学院， 西安， 710051)

自频控阵(frequency diverse array, FDA)这一概念被ANTONIK.P等人[1]于2006年提出，近年来许多学者对FDA雷达进行了系统的综述并提出了其发展方向[2-4]。与相控阵不同的是，FDA雷达在每个阵元处引入一个微小的频偏，使得其波束方向图具有角度-距离二维相关性，但其方向图存在角度和距离耦合。文献[5]提出了一种采用非均匀频偏的解耦方法，文献[6]提出了一种采用对数频偏的解耦方法，文献[7]提出了一种基于子阵阵列的解耦方法，文献[8]提出了基于遗传算法的解耦方法。

多输入多输出(multiple-input multiple-output, MIMO)雷达是一种新体制雷达，文献[9]将FDA引入MIMO雷达中，产生了FDA-MIMO雷达信号发射和接收模型；文献[10]在FDA-MIMO中引入了一种对数的非线性频偏，文献[11]引入了一种正弦频偏，两种方法都解决了距离的周期性问题；文献[12]提出了FDA-MIMO的波束形成算法。相比于MIMO雷达只能对角度进行估计，FDA-MIMO雷达能够对空间中目标的角度和距离进行二维估计。如何提高FDA-MIMO雷达对目标角度和距离的估计精度也成为了研究的重点。目前大多数研究中都建立在直达波模型上的波达方向(direction of arrival，DOA)估计算法，估计的精度受信噪比影响较大。

时间反转(time reversal, TR)技术来自于对光学相位共轭法的研究[13]。近年来很多研究人员将TR技术与雷达技术相结合[14-15]，文献[16]中提出将TR技术引入了MIMO雷达，建立了TR-MIMO模型。文献[17-18]将该技术运用于MIMO雷达目标估计领域，提高了目标估计精度。文献[19]将TR技术引入到FDA-MIMO中，但普通FDA-MIMO存在距离的模糊性，在对目标距离估计时易造成距离的多值性。图1是普通FDA的波束方向图，可以观察到其在距离上呈现周期性，造成距离模糊。图2是sin-FDA的波束方向图，引入sin函数的非线性频偏，消除了波束图在距离上的模糊，实现了距离的单值性。

图1 普通FDA波束图

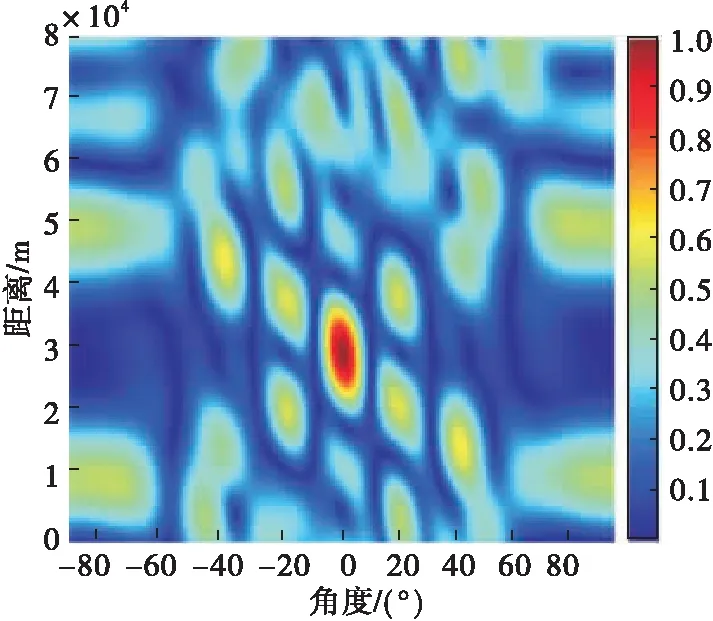
图2 sin-FDA波束图

本文主要研究TR技术对sin-FDA-MIMO的DOA估计精度的影响。

1 sin-FDA-MIMO雷达接收信号模型

为不失一般性，假设sin-FDA-MIMO雷达发射部分与接收部分位于同一位置且都为均匀线性阵列。sin-FDA-MIMO雷达发射阵元个数为M，接收阵元个数为N，阵元间距均为d，阵元间的频率增量为Δf。sin-FDA-MIMO雷达发射接收模型结构如图3所示。

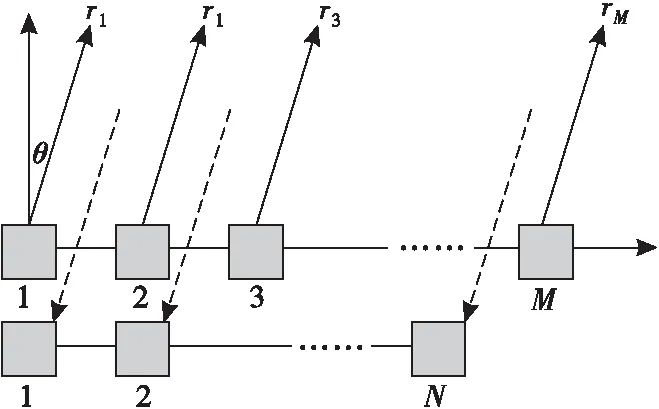
图3 sin-FDA-MIMO模型

发射阵列上第i个阵元发射的信号为:

fi(t)=si(t)ej2π[f0+sin (i-1)Δf]t

(1)

式中：si(t)为第i个发射阵元的发射波形。

假设目标符合远场条件，且有K个远场目标，则sin-FDA-MIMO第j个接收阵元接收到的信号为：

(2)

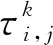
(3)

式中：Rk为第k个远场目标与阵列的距离；θk为第k个远场目标与阵列的夹角；c为光速。假设阵元的发射信号为窄带信号，则有：

(4)

假设各阵元发射信号的波形相互正交，满足：

(5)

式中：τ表示在脉冲持续时间内的时移。经过接收机内部的匹配滤波处理，可以得到接收信号导向矢量信息。对应的接收导向矢量和发射导向矢量的表达式分别为：

(6)

(7)

(8)

a(θk,rk)=ar(rk)⊙aθ(θk)

(9)

式中：⊙表示Hardamard积。对应目标信号矢量表达式如下：

(10)

式中：⊗表示Kronecker积；N∈CMN×1，是信号的噪声空间；b(θk)∈CN×1是信号接收矢量；a(θk,rk)∈CM×1为发射矢量。

由此，式(2)可以重新写为:

(11)

式中：接收信号矩阵表达式为r(t)=[r1(t),r2(t),…,rN(t)]T；发射信号向量表达式为f(t)=[f1(t),f2(t),…,fM(t)]T。

2 基于TR的接收信号模型

在sin-FDA-MIMO中，将接收矩阵r(t)经过共轭，时间反转后再次发射，则再次发射的探测信号可以表示为:

(12)

sin-FDA-MIMO再次接收到的信号为:

aH(θk,rk)f*(-t)+v(t)

(13)

式中：w(t)是TR探测时的噪声；v(t)是探测信号中的噪声n(t)与w(t)的复合噪声。将rr(t)经过匹配滤波处理后的目标信号矢量为:

(14)

3 基于TR的距离角度联合估计

3.1 Capon算法

Capon算法原理是在维持期望目标空间位置信号功率不变的基础上，使得噪声及期望目标空间位置以外的干扰信号功率最小。Capon算法的空间谱可写为：

(15)

通过式(14)对功率谱谱峰进行搜索可得对应的角度和距离。

对于sin-FDA-MIMO普通接收信号模型，式(14)中的ax=b(θk)⊗a(θk,rk)。

R=E[yHy]

(16)

对于TR的sin-FDA-MIMO接收信号模型，式(15)中的ax=a*(θk,rk)⊗a(θk,rk)。

R=E[yrHyr]

(17)

sin-FDA-MIMO雷达的DOA估计实现了目标角度和距离的二维估计，使得对目标在空间中定位变为可能。

TR-Capon算法较常规Capon算法，显著提高了目标参数估计的精度。同时，该算法利用回波信号，使其在目标处具有聚焦特性。这些表明基于TR的DOA估计算法具有良好的效果。

3.2 MUSIC算法

阵列协方差矩阵R经过特征值分解可化为信号空间和噪声空间两部分。

(18)

由噪声特征矢量与和信号特征矢量正交关系，得到空间谱表达式:

(19)

对于sin-FDA-MIMO接收信号模型，式(19)中的ax=b(θk)⊗a(θk,rk)，阵列协方差矩阵形如式(15)所示。

对于TR sin-FDA-MIMO接收信号模型，式(19)中的ax=a*(θk,rk)⊗a(θk,rk)，阵列协方差矩阵形式如(17)所示。

4 仿真试验

为了对比sin-FDA-MIMO与基于TR技术的sin-FDA-MIMO雷达距离角度估计特性，分别针对单目标和双目标进行仿真实验。设发射阵列阵元数为10，接收阵列阵元数为10。阵列阵元间距d=λ/2，载频f0=9 GHz，频率增量Δf=10 kHz，信噪比为0 dB，快拍数L=200。

4.1 单目标

假设目标位置位于(30°,50 km)，图4为sin-FDA-MIMO的Capon谱MUSIC谱、TR-Capon谱和TR-MUSIC谱。图5为4种距离角度估计算法的均方根误差(RMSE)比较。设置300次蒙特卡洛试验，信噪比间隔设置为2 dB。

图4 单目标距离角度估计

图5 均方根误差变化情况

计算角度RMSE公式如下：

(20)

计算距离RMSE公式如下：

(21)

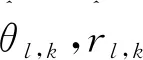
从图4可以看出4种DOA估计方法得到的不同样式的空间谱，TR-Capon和TR-MUSIC得到的空间谱与常规接收信号模型下的Capon和MUSIC算法相比，具有更高的空间估计聚集性和更低的旁瓣分布。

图5实验结果显示TR-Capon和TR-MUSIC在角度和距离估计的RMSE都较Capon和MUSIC算法有明显的下降，验证了TR技术对提高DOA估计的有效性。

4.2 空间位置接近的双目标

假设目标位置位于(20°,28 km)和(23°,30 km)，图6为处于相近空间位置的两个目标的空间谱估计。可以看出普通Capon和MUSIC的空间谱分辨不出空间中的两个目标，而基于TR技术的Capon和MUSIC的空间谱则能够明显区分。

图6 双目标距离角度估计

图7为4种参数估计算法在不同信噪比条件下的均方根误差(RMSE)比较。设置300次蒙特卡洛试验,信噪比间隔设置为2 dB。图7定量地说明了TR技术对相近空间位置的两个目标的空间估计能力有显著提高。

图7 均方根误差变化情况

5 结语

TR技术对于sin-FDA-MIMO的距离角度联合估计精度有较显著的提高，且对于空间位置相近的目标有较强的分辨能力。

本文建立了sin-FDA-MIMO模型，该模型可以实现在距离和角度上进行二维估计。在传统Capon和MUSIC算法的基础上，将TR技术分别融入这2种算法，并对这4种算法进行了距离角度估计精度的比较，通过计算不同信噪比下各算法的RMSE，验证了TR技术对提高二维估计精度的有效性，为提高sin-FDA-MIMO雷达在距离和角度估计精度提供了一定的参考。