等离子体流动控制的前掠翼静气弹发散主动抑制

张钧奕， 苏新兵， 赵希玮， 王 振

(空军工程大学航空工程学院， 西安， 710038)

前掠翼具有高升阻比、失速迎角大等优势，但前掠翼的静气弹发散问题一直制约着其发展和应用[1-3]。国内外学者针对前掠翼气动弹性现象与抑制静气弹发散进行了许多研究[4-5]，主要手段有气动弹性剪裁[6]、操纵面偏转[7]与应用复合材料[8]。近年来，流动控制技术发展迅速，给前掠翼静气弹抑制提供了新的思路。流动控制主要包括主动流动控制与被动流动控制，主动流动控制的优点在于可以根据不同的飞行条件与流动特点进行相应的改变以适应不同工作环境。

等离子体流动控制是基于“等离子体气动激励”的新概念主动流动控制技术[9-10]，它的优点是无需运动部件，对于机翼流场主动控制具有重要意义。国内外学者针对等离子体流动控制技术进行了大量的试验和仿真研究，其作用原理是通过设置于物体表面的电极将附近的空气电离，产生“离子层”，并使等离子体在电场力作用下运动，通过带电粒子与中性气体分子的碰撞，诱导物体表面空气定向流动，产生射流[11-12]。目前一种重要手段是通过表面介质阻挡放电[13](DBD)使等离子体激励器产生定向射流，主要有两大作用：一是增大附面层的流动速度；二是向附面层注入能量，提高低能流和高能流的掺混，增强其抵抗逆压梯度的能力[14]。Shyy Wei等提出了对介质阻挡放电进行简化的唯象学模型[15-16]，为等离子体流动控制数值仿真提供了新的思路。

随着计算机性能的提高，流固耦合(CFD/CSD耦合)技术成为研究气动弹性问题的一种重要数值仿真方法[17]，刘万钢等对自由飞行状态下的细长弹箭进行了静气弹计算[18]，雷帅等基于AnsysWorkbench对HIRENASD机翼静气弹特性进行了仿真研究[19]。本文借鉴上述研究思路与方法，将等离子体流动控制技术与流固静力耦合技术相结合，通过数值模拟，初步验证了在前掠翼表面布置等离子体激励器进行流动控制以抑制静气弹变形的可行性，其中等离子体流动控制的仿真计算采用唯象学模型，流固静力耦合采用Fluent与Mechanical进行联合仿真，唯象学模型通过UDF在动量方程中添加体积力源项实现。

1 计算方法与模型

1.1 流场求解技术

采用基于有限体积法的Fluent模块求解三维定常Navier-Stokes方程，在笛卡尔坐标系(x1,x2,x3)中，定义速度分量为(u1,u2,u3)，根据Einstein求和约定，无热源三维Navier-Stokes方程的守恒形式为：

(1)

式中：φ为状态矢量；Fi为对流通量矢量；Fvi为黏性通量矢量，S为源项矢量，用列向量形式表示如下：

式中：ρ、p、f、E、H、T分别表示密度、压力、体积力、总能量、总焓和温度；黏性应力张量为：

(2)

式中：k、μ、λ分别表示流体热传导系数、分子黏性系数和第二黏性系数；δij为克罗尼柯尔符号，当i=j时τij为正应力，i≠j时τij为切应力。

1.2 结构求解技术

采用基于有限元法的Static Structural模块求解结构静力平衡方程：

(3)

式中：δ(t)为节点位移分量矩阵；R(t)为节点载荷矩阵；M、C、K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵。

Kδ(t)=R(t)

(4)

采用基于Newton-Raphson方法[20]的迭代求解进行结构计算，逐步增加特定载荷求解结果，考虑结构的几何非线性，在每一次迭代时根据结构新的几何位置坐标形成新的刚度矩阵。

1.3 前掠翼模型

本文采用的前掠翼数值计算模型如图1所示，选用NACA0015翼型，翼型后缘为半径0.003 m的圆弧(此模型也被用作进行基于Coanda效应对钝后缘机翼流动控制的相关研究)；机翼前、后缘掠角分别为41.19°和54.07°；机翼半展长为0.4 m；平均空气动力弦为0.204 m；展弦比为4.3；根梢比为3.4。

图1 前掠翼模型尺寸

1.4 等离子体唯象学模型

介质阻挡放电等离子体激励器的仿真模拟有多种方法，唯象学模型是对复杂的等离子体激励流动的一种简化，以对流体施加一定的电场力作为等离子体激励形式，通过在动量方程中添加体积力源项实现功能，有利于嵌入流体仿真软件进行计算。本文采用的等离子体唯象学模型的平面图如图2所示。

图2 等离子体唯象学模型

在△OAB区域内电场力沿线段AB呈线性分布，方向为由A指向B，其具体分布为：

E(x,y)=E0-k1x-k2y

(5)

Ftave=ϑαρcecΔtE(x,y)δ

(6)

式中：ϑ为电源电压频率；α为电荷碰撞效率因子；ρc为电荷数密度；ec为元电荷电量常数；Δt为一个周期内的放电时间；δ为狄拉克函数，在基于有限体积法的N-S方程求解中，狄拉克函数在定义域内的积分值为1。

等离子体激励区域如图3所示，等离子体激励器布置在机翼前缘外侧上表面处，激励区域呈三棱柱形，其在翼型平面内的投影均为图2所示的三角形激励区域。由于布置在机翼表面，等离子体激励区域与机翼表面的重合面并非严格意义上的平面，但由于其弯度较小，在计算时可以看作平面处理。本文所用的流固耦合方法与等离子体唯象学模型在文献[13]、[19]中已有验证，可以保证仿真计算的正确性和可信度。

图3 等离子体激励区域

1.5 网格划分

采用结构网格分别对流体域与固体域进行网格划分，计算采用半模，远场尺度约为20倍机翼弦长，无量纲化壁面距离y+≈1，流体与固体网格数量分别为2 815 826与116 812，等离子体激励流体域网格数为31 407，流场网格如图4所示。

图4 流场网格

较高的网格质量是流固耦合仿真运算的关键，关系网格运动是否合理和耦合运算的成败，由于等离子体激励区域呈三棱柱形状，所以在划分网格时采用Y形网格进行处理，保证了即使在尖角处网格纵横比仍大于0.8。

流体域面网格与结构域面网格采用节点一致化方案，优点是可以消除因界面网格交错产生的插值运算误差，提高计算速度和精度。

等离子体唯象学模型通过在Fluent中加载UDF的形式在动量方程中添加体积力源项实现，传统的UDF以网格坐标的不等式来限定等离子体激励区域，这种方法多用于网格数量较小时的流动计算，如对平板流动进行激励。但对于网格数量较大的机翼流固耦合仿真运算，本身运算量很大，以不等式形式在外流场通过遍历网格坐标来定位激励区域将耗费大量的时间，因此采用划分多流体域的形式将等离子体激励区域的流体独立划分，划分时可采用自顶向下与自底向上相结合的方法与布尔运算分割流体域。等离子体激励流体域与外流体域的交界面类型为interior，优点是减小插值运算误差，提高计算精度。

2 计算结果与分析

流体计算采用压力远场边界，其中p=1.01×105Pa，T=288.15 K，Ma=0.4，α=3°，湍流模型选择k-ωSST模型，黏度采用Sutherland动力学黏度关联式进行计算，动态网格采用平滑、分层方法，收敛残差为10-4，采用二阶迎风格式，压力速度耦合方式采用Coupled算法，机翼表面为无滑移壁面。

在唯象模型中，a=5.773 mm、b=10 mm、d=0.83 mm、ϑ=3 kHz、ρc=1×1017m-3、ec=1.602×10-19、U0=20 kV、Eb=3×103kV/m、t=67 μs，由此可以得到E0=24 MV/m、k1=21 MV/m、k2=36.4 MV/m，代入式(6)中即可求得等离子体激励区域内各点的体积力。以上面给定参数为基础，通过调节式(6)中的变量，可以实现不同倍数的激励强度。

将机翼简化为具有各向同性材料的固体，激活大变形选项，在翼根施加固定约束，材料密度ρ=10.2 t/m3，杨氏弹性模量为E=200 MPa，泊松比为0.394，剪切模量为G=318.9 MPa。根据力与位移的L2范数小于缺省的收敛准则作为收敛标准。在流固耦合面进行力与位移的数据传递，耦合面变量收敛残差为10-2。当耦合迭代20次时，流场求解器与结构求解器分别收敛且耦合面残差收敛，可以认为耦合计算收敛。

在上述条件下，分别对不施加激励与施加不同强度激励下的机翼外流场进行计算。图5给出了施加激励前后机翼上表面流场的流线图。

从图5可以看出，未施加激励时前掠翼分离区主要位于翼根后部；施加激励后，加速的部分流体与未受加速的流体之间产生黏性剪切力，在激励区域的两侧，受到剪切力作用的流体发生变形并诱导出具有一定强度的旋涡，由于上翼面流体具有沿展向的分速度，所以旋涡向翼根方向偏转。

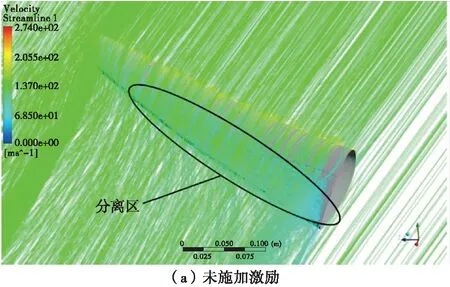
图5 外流场流线图

图6给出了施加等离子体激励前后机翼75%展向位置的压力云图。

图6 y/b=75%位置压力云图

从图6可以看出，未施加激励时，机翼展向75%位置处下表面前缘对来流起阻碍作用导致压力较大，上表面前缘由于流体的Coanda效应导致压力较小。施加激励后，由于电场力做功对流体注入能量使总能量增大，压力势能和动能均增大，上表面处于激励位置的流体压力增大，而下表面无明显变化。

图7给出了50%、75%、97.5%展向位置的速度云图。

图7 机翼外侧速度云图

从图7可以看出，受激励流体的动能增加表现在受激励位置的速度有不同程度的增大，其中在激励位置内侧边缘速度最大，这是由于此处流体受到电场力、压差力和诱导的旋涡加速等多重作用。

图8给出了施加激励前后分别在2.5%、25%、50%、75%、97.5%展向位置的压力系数变化情况，其中实线表示未进行激励，虚线表示进行激励，横坐标为空间绝对坐标，由于机翼前掠，坐标值从小到大分别表示翼尖到翼根、前缘到后缘的不同位置。

从图8可以看出，与未施加激励相比，施加激励后流体受到电场力做功，能量增加，压力增大，沿展向外侧前缘吸力面的压力系数绝对值先减小后增大，外侧前缘上下表面压差逐渐减小，且这种减小的程度随激励强度的增大而增大。激励后机翼上表面外侧前缘压力增大，下表面压力无明显变化，由于压差作用将产生低头力矩，使翼尖的弹性变形减弱。从图8中还可以看出，随着激励强度的增大，内侧上表面压力系数的绝对值有一定程度的减小，而下表面变化不明显，导致翼根的升力也有一定的减小。

图8 压力系数变化

图9给出了不同激励强度下机翼弹轴挠度的变化情况。

图9 弹轴挠度

从图9可以看出，在不施加激励时，前掠翼由于气动弹性效应使弹轴在翼尖处具有较大的挠度，进行等离子体流动控制后整个弹轴的挠度都有所降低，其中翼尖的挠度变化最为明显，挠度降低了8.5%～23.7%，说明在进行流动控制后机翼受到的弯矩减小。

图10给出了翼尖扭转角与机翼结构变形最大应力随激励强度的变化情况。

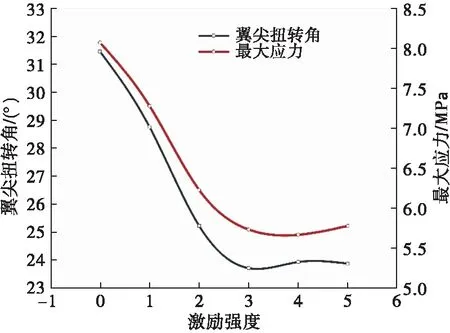
图10 翼尖扭转角与最大应力变化

从图10可以看出，翼尖的扭转角随激励强度的增加降低了8.6%～24.7%，最大应力降低了9.8%～29.8%，说明在进行流动控制后机翼受到的扭矩减小。

由此可见，在前掠翼前缘外侧上表面处布置等离子体激励器后进行流动控制时，机翼弹轴的弯曲变形和翼尖的扭转变形都得到了不同程度的抑制，说明机翼的受弯扭程度降低，抵抗静气弹发散的能力增强。

图11给出了在进行流动控制过程中，升力系数、阻力系数、弯矩系数和扭矩系数随激励强度增加的变化情况。

图11 气动特性参数变化

从图11可以看出，随着激励强度增强，升力系数、弯矩、扭矩系数有不同程度的降低，阻力系数变化相对较小。说明将等离子体激励器布置在机翼前缘外侧上表面处，在一定程度上提升机翼抵抗弯扭变形的能力，对其静气弹发散问题能起到较好的抑制作用，但同时以牺牲部分升力等气动特性为代价，需要进一步采取措施进行气动补偿。

3 结论

本文针对前掠翼静气弹发散的主动抑制问题开展研究，基于等离子体流动控制与流固双向静力耦合技术，通过仿真计算，得出如下结论：

1)利用等离子体流动控制技术可以改变弹性前掠翼表面的气动力分布，通过等离子体的激励作用，受激励的流体从电场中吸收能量，压力增大，流速加快。

2)在弹性前掠翼前缘外侧上表面布置激励器进行等离子体流动控制可以在一定程度上降低机翼弹轴的挠度，减小翼尖扭转角，达到较好抑制静气弹发散的目的，且随着激励强度的增大，抑制效果逐渐增强。

3)将等离子体激励器布置在机翼前缘外侧上表面处，进行等离子体流动控制对前掠机翼弹性变形进行抑制的过程中，机翼受弯曲和扭转的强度减弱，阻力没有明显变化，但升力等气动特性有一定程度的损失，且随着激励强度的增大，升力损失逐渐增大，需要进一步采取措施进行气动补偿。