新型双旋流燃烧室热声振荡的实验研究
何祖强, 王 平, Meenatchidevi Murugesan, Antonio Ferrante,3, 李伟超, 姜霖松
1. 江苏大学 能源与动力工程学院, 江苏 镇江 212013; 2. 江苏大学 能源研究院, 江苏 镇江 212013;3. Centro Combustione Ambiente Spa, vicinale Milano km1. 600, 70023 Gioia del Colle (Ba) Italy
0 引 言
在现代燃气轮机的相关研究中,常采用贫燃预混燃烧技术(LP)实现污染物控制和燃烧效率之间的平衡。通过结合变几何、分级燃烧等措施,降低火焰温度,减少NOx排放。由于热声耦合效应,这些技术也带来了贫燃预混燃烧中最具挑战性的问题之一——燃烧振荡问题。燃烧振荡会产生高强度噪声,损坏燃烧室,还会造成熄火和回火现象,危害燃气轮机正常工作。在燃烧过程中存在当量比波动,加之流场自身的不稳定性(如涡脱落等[1]相干流结构),往往导致热释放率也产生波动,在热释放率波动与压力波动相互耦合的过程中,当声场获得能量大于耗散能量时,将形成一个正反馈回路,产生共振现象。
在贫燃预混燃烧中常常采用旋流结构来稳定火焰,而旋流稳定的火焰中通常还伴有各种微结构的火焰。不同的火焰形态反映了燃烧室内不同的声波动,这些形态一般被概括为紧凑型火焰、M型火焰和V型火焰[2-3]。火焰形态往往与燃料组成、当量比、雷诺数、来流速度、旋流数、燃烧室开放程度以及中心钝体结构有关,这些参数的改变也会引起燃烧过程模态的转变。
大量研究表明,热声振荡是多种物理现象相互耦合的复杂过程,涉及到声学、流体力学、传热学、燃烧学等多个学科。实验研究是掌握热声振荡特性的重要手段。国内研究者通过设计不同的燃烧试验台或对某一经典燃烧室模型开展不同燃烧方式下的热声振荡研究,掌握了相关燃烧室热声耦合现象的发生过程及机理。房爱兵等[4]以含氢合成气为燃料,在全尺寸中压试验台上测量了预混火焰和扩散火焰的燃烧振荡过程,揭示了氢含量对火焰形态和燃烧不稳定性的影响。在以单旋流燃烧器为核心的常压预混燃烧试验台上,张昊等[5-6]对天然气预混燃烧过程中的热声耦合振荡现象进行了研究。结果表明:振荡频率随当量比的减小有所增大,但未发生模态变化;在常压条件、接近贫燃熄火极限时,热声耦合振荡现象消失,压力脉动频率跃升至500或 1000 Hz附近的高频。杨甫江等[7]利用贫燃预混单旋流燃烧试验台研究了常温常压下当量比对燃烧不稳定性非线性发展的演化过程,在线性火焰模型的基础上增加饱和因子构建热声网格模型,并以此预测热声振荡的极限环幅值。结果表明:随着当量比提高,燃烧经历了稳定-不稳定-极限环的变化过程,振荡频率变化不大,而脉动压力幅值显著增大,并最终达到极限环状态。林枫等[8]在低压模化燃烧实验台上完成了某型燃气轮机全尺寸振荡燃烧特性实验研究,总结了燃料量、当量比对50 Hz上下的主频振荡的影响及其变化规律。
燃料与空气预混后,经旋流结构进入燃烧室,产生中心回流区稳定火焰,促进燃料和空气充分混合,从而达到提高燃料利用率、减少污染物排放的目的。但燃烧时的热声振荡不可避免,且会因燃料种类、入流参数、旋流器及燃烧室结构的不同而呈现出不同的振荡规律。针对不同的影响参数,国外研究者采用可视化测量手段开展了相关实验研究。通过改变燃烧室下游的长度,Taamallah等[9]研究了火焰的形态转变及不稳定性,在长、短两个燃烧室中观察到相同的火焰宏观结构;与短燃烧室相比,长燃烧室外部再循环区(ORZ)火焰的出现与热声振荡同时发生;但在近似的当量比处,短燃烧室中并未发生热声振荡现象。Fritsche等[10]研究了不同入口温度和当量比下的稳定和不稳定的旋流火焰,时间平均的平面激光诱导荧光(OH-PLIF)图像表明,贫燃旋流火焰不稳定性过渡的特征是火焰位置和结构的突变,表明不同的火焰稳定机制因火焰温度的不同而存在。Durox等[11]通过改变叶片角度研究了2种类型(一种引起低频振动,一种对应于较高的频率模态)的不稳定性。结果表明,适当调节旋流数(通过改变叶片角度),可以避免不稳定区域的出现,从而避免热声振荡的发生。Kim等[12-13]研究了旋流燃烧中掺氢火焰的传播速度及含氢量对火焰结构转变及热声振荡的影响。结果表明,随着预混火焰传播速度增大,火焰从V型转变为M型。与V型火焰相比,M型火焰能够抑制流动的扰动。掺混高摩尔分数H2的天然气火焰在燃烧动力学上更稳定,但却会与系统的高频热声本征模态耦合。
以往开展热声耦合振荡研究,多以射流、黎开管、单旋流为研究对象;而双旋流作为一种先进的稳定火焰结构,针对其开展的热声耦合振荡研究还比较少。本文基于自主设计的振荡燃烧可视化试验台及核心部件双旋流燃烧器,利用压力传感器、LabVIEW动态测量系统和高速相机,在不同工况下测量双旋流燃烧室内的压力脉动变化,通过后处理得到燃烧过程中的非线性时间序列,具象化分析功率谱及极限环,并以高速相机记录的火焰结构研究双旋流火焰结构转变和双旋流燃烧室的热声振荡特征。
1 实验装置及测量工具
实验采用自主设计的基于双级同心轴向旋流器的燃烧装置(如图1所示),主要由同心双管道、双级旋流器和方形燃烧室组成。预混气体(甲烷与空气)从同心双管道(预混段)通入,经双级旋流器进入燃烧室内点火燃烧。同心双管道内管长1100 mm,外管长960 mm(经前期计算分析,管长可以保证气体在出口处达到完全预混效果);内管内直径D1=11 mm,壁厚1 mm,外管内直径D2=21 mm。出口采用收缩管结构(收缩比为0.5),可以使流动加速,产生很强的出口涡旋,有效消除上游旋流引起的逆压梯度[14]。燃烧室侧壁为耐高温的石英玻璃,便于使用光学仪器进行测量。

图1 双旋流燃烧器结构简图Fig.1 Geometric sketch of dual-swirl burner
新型双旋流器安装于同心双管道与燃烧室之间(如图1所示)。该旋流器为同向旋流器(几何结构如图2所示),内旋与外旋旋向相同(旋流角度为120°)。采用共轴同向的固定导叶,共8个旋流叶片(厚度0.6 mm),沿中心钝体(直径2 mm)周向布置。经计算,旋流数为0.53。
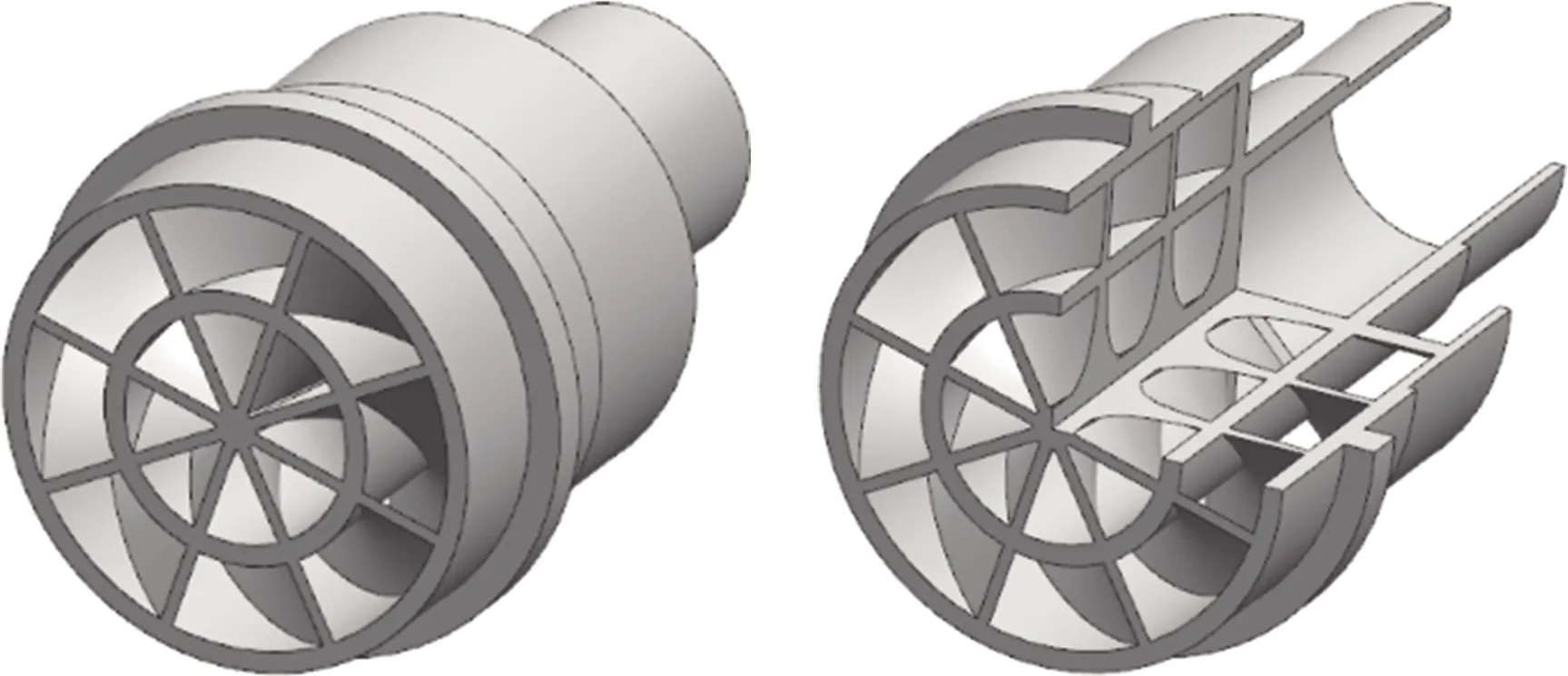
图2 双级旋流器几何结构图Fig.2 Geometry structure of dual swirler
采用美国PCB公司103B02动态压力测量传感器(6551)测量声压。该传感器的线性度为0.5% FS,误差范围为1%,灵敏度为225.4 mV/kPa。以NI公司的CompactDAQ控制器连接传感器与PC端。使用LabVIEW实时检测和采集流场压力信号,采样频率8192 Hz,总采样数49 152。通过HORIBA公司的数字式质量流量控制器(MFC)S600快速精确地控制内外管空气和甲烷,控制空气和甲烷流量的质量流量计的最大量程分别为250和30 L/min,误差控制在1%以内,则当量比的相对最大误差为1.4%。通过化学图像发光并同步使用高速相机(Photron FASTCAM SA-Z)以2000 Hz的采样率(在发生热声不稳定时为5000 Hz)拍摄火焰图像。
2 实验结果与分析
本文从非线性动力学角度研究燃烧的不稳定现象。首先基于高速相机图片和基本的功率谱密度图分析了不同过程下的振荡特征,然后开发了先进的非线性极限环分析技术,使用一种新型数字信号处理方法重构相空间,对所获压力实验数据进行表征,详细分析双旋流燃烧室内的热声振荡现象。
根据状态参数改变策略的不同,本文选定了2种实验过程(“过程1”研究当量比的影响:保持甲烷体积流量不变,先逐步减小、再逐步增大当量比;“过程2”研究体积流量的影响:保持当量比不变,逐步增大预混气体积流量)。在2种过程中,均进行多次测量进行对比,实验结果在室内常温常压下具有可重复性。
2.1 过程1:研究当量比的影响
由扰动引起的化学当量比变化,是燃烧不稳定和自激振荡的重要诱因。本节开展“过程1”实验研究:以质量流量控制器(MFC)控制内外管甲烷流量均保持为3.5 L/min,通过调节空气流量,逐步改变当量比;在当量比φ=1.000条件下点燃预混气,待其稳定燃烧后,逐步将预混气当量比从0.900减小至0.725,而后再从0.725逐步增大至0.925。表1列出了“过程1”实验中的8个工况(Case A~H)及对应的当量比。

表1 Case A~H对应的当量比Table 1 Equivalent ratio corresponding to Case A~H
实验过程中,采用LabVIEW软件同时进行高速相机拍照和压力数据采集(图3为通过高速相机得到的2种火焰结构照片)。对压力数据进行处理,将不同当量比下的压力脉动幅值和火焰结构变化情况汇总于图4。图中,I和II分别表示当量比减小和增大方向;V和M表示火焰的2种结构;A~H表示工况Case A~H。
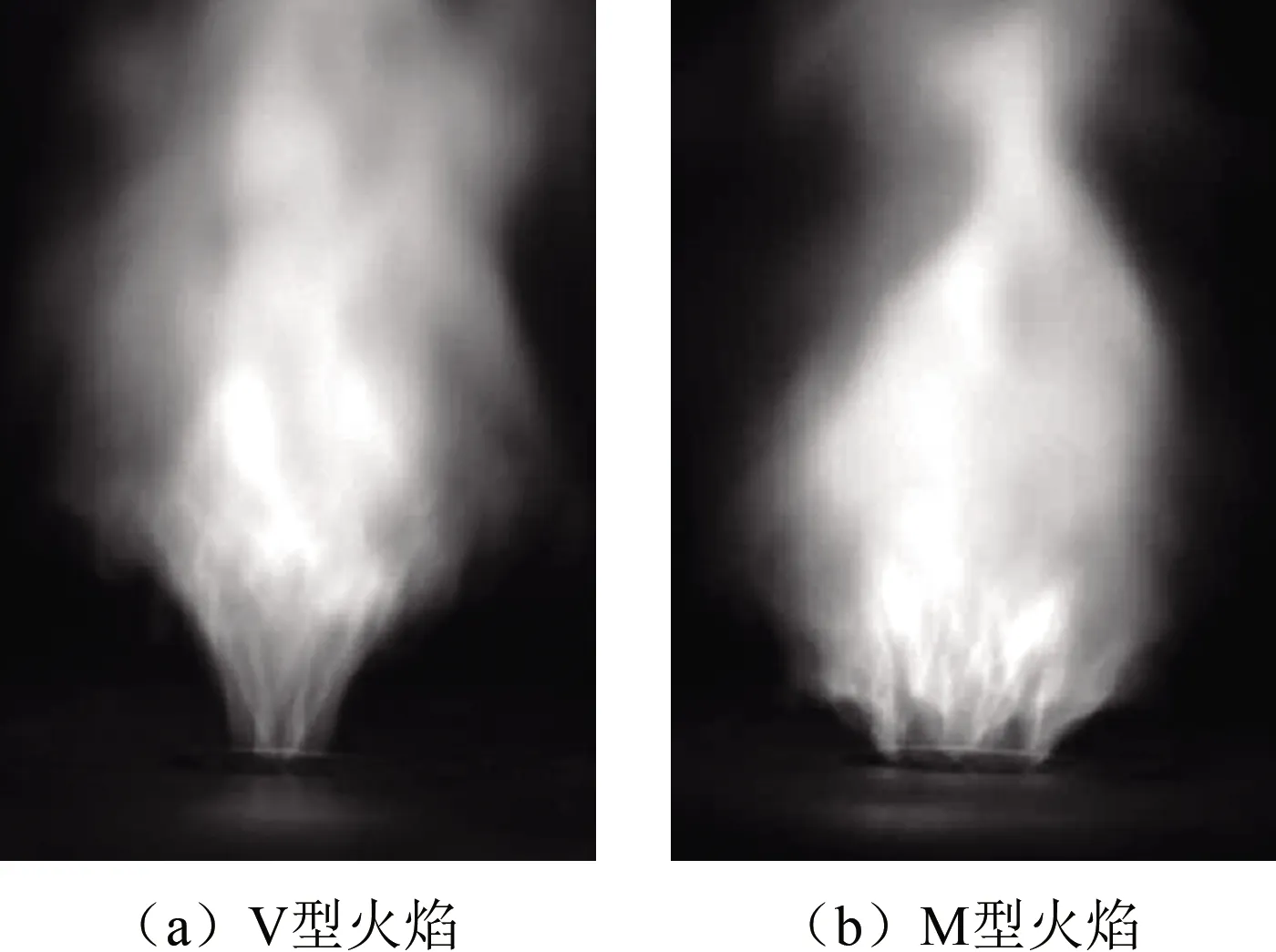
图3 不同火焰结构Fig.3 Different flame structures
从图4中可以看到,当量比为0.900时,压力脉动振幅高达525 Pa,火焰为M型。逐步减小当量比至0.800,观察到火焰由M型向V型转变,此时的压力脉动振幅也减小至150 Pa左右。在当量比降至0.725并保持一段时间后,逐步将当量比增大至0.800,此时火焰并未从V型向M型转变,压力脉动振幅也未达到之前的150 Pa左右。直到当量比增大至0.925时,M型火焰才再次出现,呈现不稳定燃烧状态。

图4 不同当量比下火焰结构变化及压力脉动幅值Fig.4 Structural change of flame and pressure pulsation amplitude at different equivalence ratios
以pwelch方法(Welch平均功率图法)对所采集的时序信号进行分析,得到当量比变化过程中的功率谱密度图(PSD),如图5和6所示。结合图4和5可以发现,在当量比从0.900减小至0.800的过程中,出现M型火焰,双旋流燃烧室内出现持续的不稳定现象,激发了最大振幅模态的二阶谐波,此过程中的主频率均介于该频率下一阶波激起的二阶谐波和燃烧室内1/4波(预混段、燃烧室组成的“壁面”以及旋流器相互耦合形成的声学振荡频率)之间。随着当量比减小,不稳定现象逐渐减弱,在功率谱上反映为声压级从53.94 dB减小至40.62 dB,如图5(a)~(c)所示。在转变为V型火焰后,压力脉动振幅突然减小,但在图5(d)中并未发现不稳定的主频率,此时处于稳定燃烧状态。
而后,在逐步增大当量比的过程中(当量比由0.725增大至0.900),燃烧室处于稳定燃烧状态,如图6(a)~(c)所示。当量比增大至0.925时,不稳定现象再次出现(主频率为396.5 Hz),火焰从V型转变为M型。在M型与V型火焰的功率谱图中,除窄带高频脉动外,都存在一个频率为50.0 Hz的低频振荡。通过分析可知,这是由双旋流产生的回流区内的燃烧不稳定所导致的[15]。
在图4的当量比变化的子过程I和II中,M型和V型火焰的临界转变点差别很大。结合图5和6的功率谱图分析,燃烧稳定和不稳定状态的转变可能存在一定的时间记忆效应,后期燃烧状态受前期燃烧状态影响,即存在“滞环现象”。一般而言,滞环现象的出现和系统非线性过程相关,在当量比减小的子过程I中,可能存在不稳定正反馈过程。当子过程I发生不稳定现象时,双旋流形成的复杂流场(如回流区、剪切层)以及进动涡核(PVC)与燃烧室的声模态相互耦合,在短时间内形成正反馈循环,从而使火焰在当量比减小至0.800之前继续保持M型;当量比减小至0.800时,M型向V型火焰转变,此时正反馈循环已被破坏。当持续至子过程II、当量比增大至0.900时,火焰已经维持了一段时间的稳定(在双旋流流场内外剪切层的基础上维持V型火焰不变)。因此,在研究双旋流热声振荡问题时,需重点关注其复杂的流场结构。



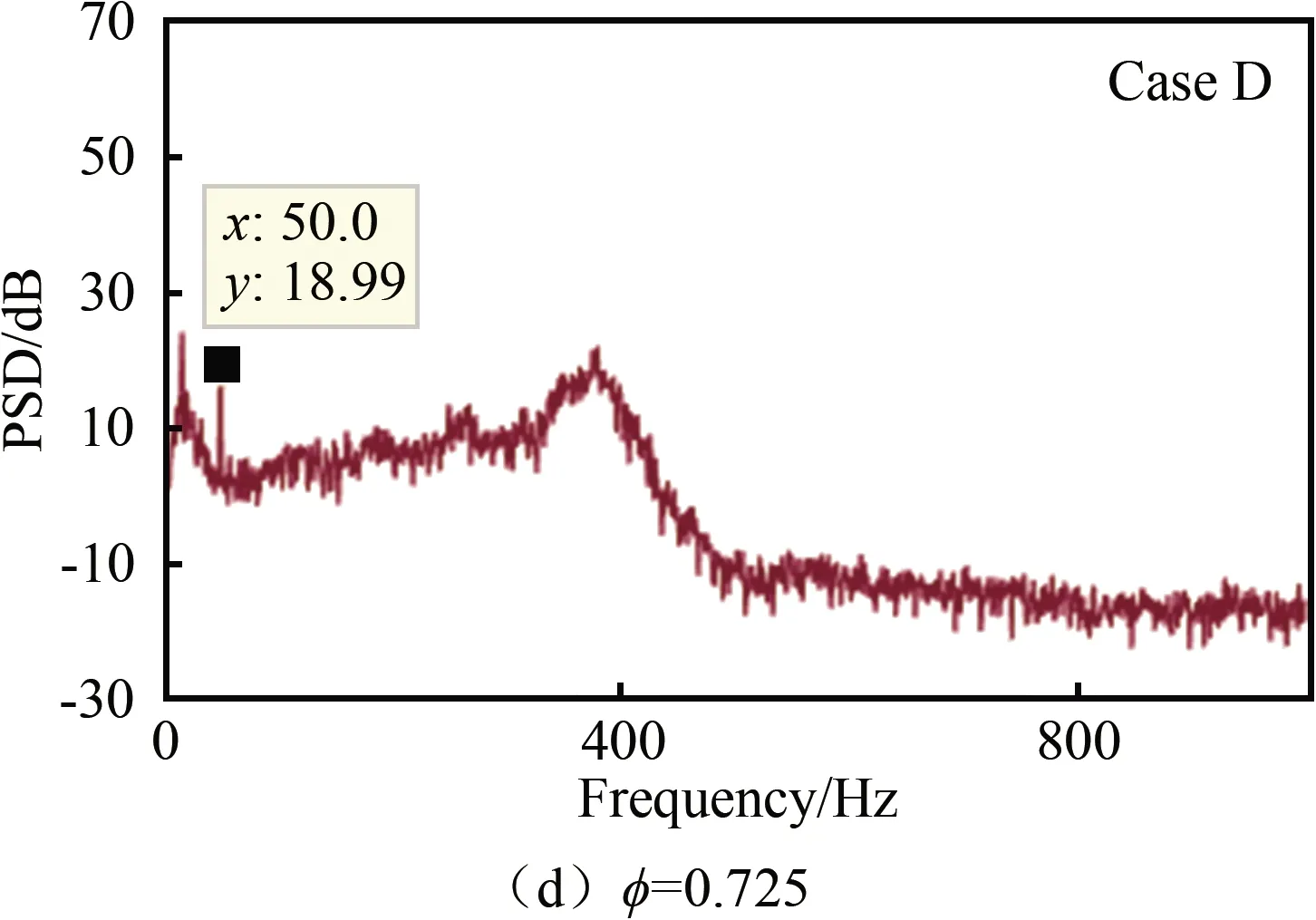
图5 当量比减小时的功率谱图Fig.5 Power spectrum when the equivalence ratio decreases

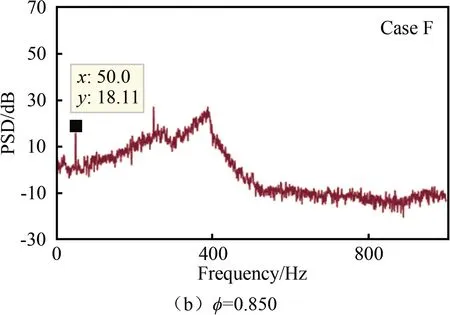
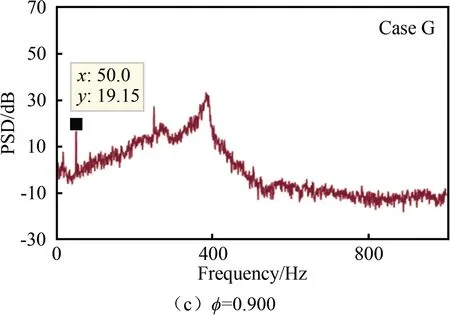

图6 当量比增大时的功率谱图Fig.6 Power spectrum when the equivalence ratio increases
2.2 过程2:研究体积流量的影响
通过控制新型双旋流燃烧室内、外管的预混气流量,可以研究其对燃烧室的振荡频率和声压级的影响。在“过程2”实验中,保持内、外管为相同的当量比φ=0.850;外管保持甲烷流量Vf1=4.0 L/min、空气流量Va1=45.0 L/min不变;通过MFC调节内管甲烷流量Vf2和空气流量Va2,使其从最初的0.8和9.0 L/min持续增大至5.5和62.0 L/min。表2列出了“过程2”实验中的Case I~L等4个工况。
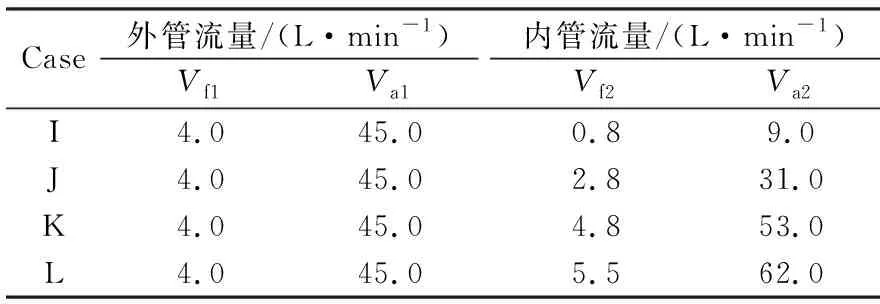
表2 Case I-L对应的内外管体积流量Table 2 The Volume flow rate of inner and outer pipes corresponding to Case I-L
图7为表2各工况下的功率谱图。如图7(a)所示,当内管中体积流量最小时,发生了热声振荡,其主频率为256.0 Hz,该频率下一阶波仍然激起了其最大振幅模态的二阶谐波,介于其激起的二次谐波和燃烧室内1/4波之间。从图7(b)可以发现,此时主频率为260.0 Hz,基本无变化,但振荡明显减弱,声压级由最初的54.50 dB降为30.02 dB。从内管甲烷、空气流量为2.8和31.0 L/min时(出现417.5 Hz),直至最后增大为5.5和62.0 L/min时(411.0 Hz为主频率),火焰一直保持为V型。在Case L工况下,主频率为411.0 Hz,声压级仅增加至38.02 dB,尚未达到Case I的水平。各工况下的热声振荡特性及火焰结构如表3所示。通过本实验发现:在不改变当量比的情况下,可以通过改变体积流量来改变燃烧的稳定状态。

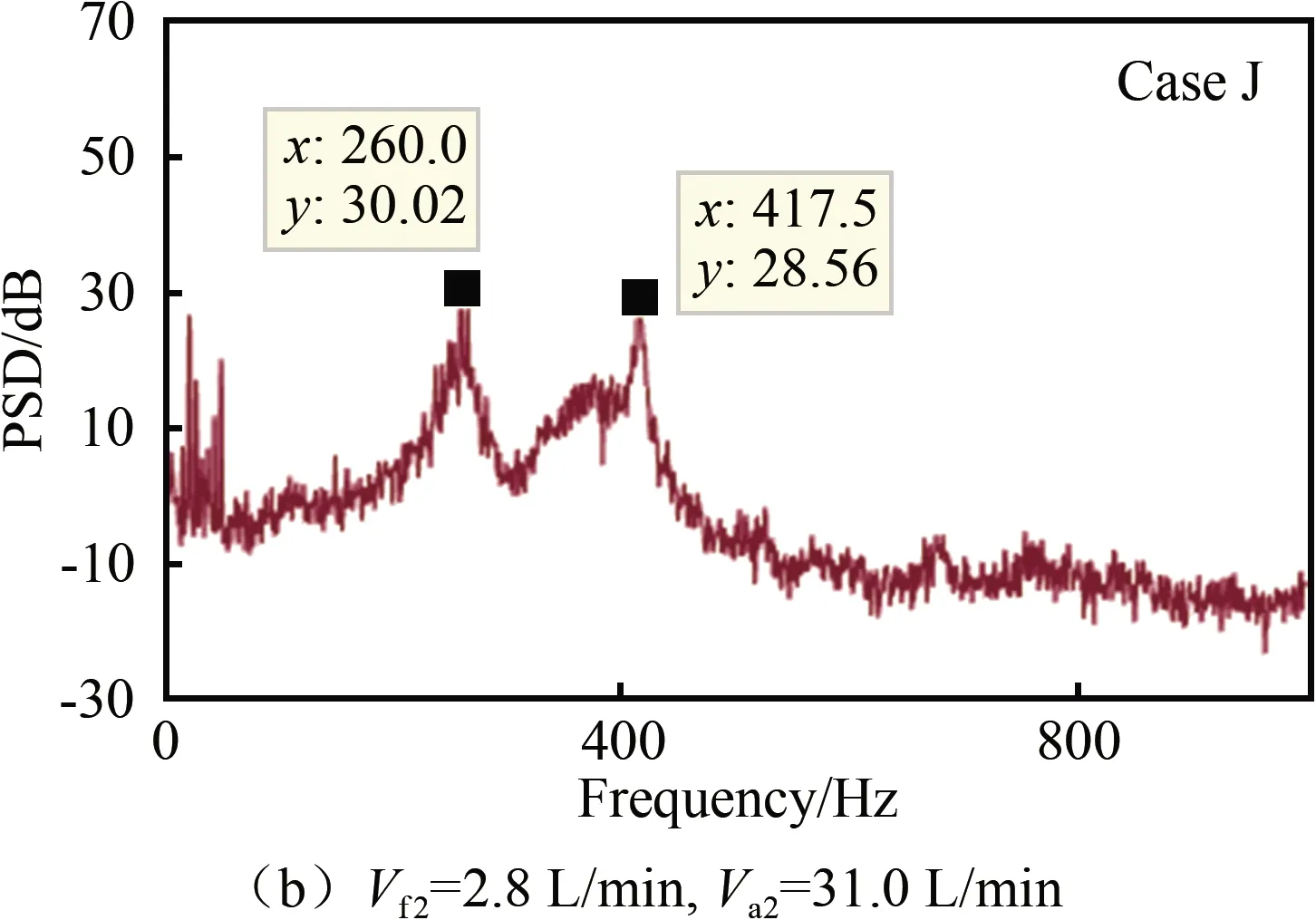


图7 φ=0.850时内管体积流量变化下的功率谱图

表3 各工况下的热声振荡特性及火焰结构Table 3 Thermoacoustic oscillation characteristics and flame structure under corresponding working conditions
在改变体积流量的“过程2”实验中,内外管中皆为甲烷和空气的预混气,因此不需考虑燃料介质性质的差异。外管甲烷、空气流量分别维持4.0和45.0 L/min不变,而内管的甲烷、空气流量从最初的0.8和9.0 L/min增大至5.5和62.0 L/min。结合表3及图7、8可知,内外管预混气总流量越大,燃烧室的总功率越大,发生燃烧振荡时在功率谱图上的主频率越高(由最初的256.0 Hz升至最后的411.0 Hz)。内管预混气的体积流量最初远小于外管,之后则大于外管,流量相对大小的变化导致火焰传播相对速度发生变化,火焰结构的内部剪切层也发生相应变化,在高速相机中呈现为不同扩张角度的V型火焰(如图8所示),表明前后两者内部中心回流区的大小和长度存在区别,导致了燃烧稳定性的改变。在后续实验中,可以通过测量放热率作进一步分析。
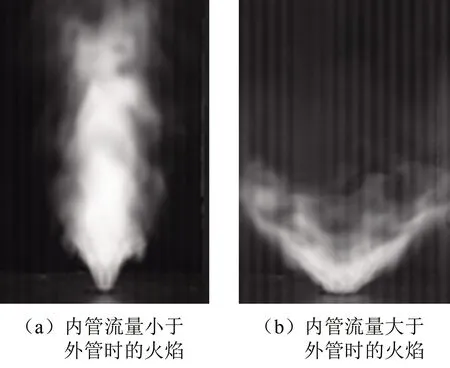
图8 不同角度的V型火焰Fig.8 V-shaped flames with different angles
3 相空间重构分析
为深入分析新型燃烧器的热声振荡特性,需进一步提取复杂非线性过程的详细信息。基于相空间的非线性时间序列分析方法是系统分析和识别由非线性过程产生的时间序列数据特征和结构的重要工具。
相空间重构方法,是利用实验得到的时间序列数据建立一个多维空间来重构动力系统的时间演化过程。若系统得到的所有状态变量(包括所需导数)在任何时候都是已知的,则可确定一个动态系统。通常,系统各状态通过其导数相互关联,可以用一个被测系统单个状态的长度空间进行表述。
Takenshas[16]证明了从测量得到的时间序列中提取延时坐标点构建多元相空间的方法,该方法可以用于进行有效的非线性系统特性分析。在得到的坐标系中,重构的相空间矢量点表现出与原动力系统相同的特性:
y(m)=[s(m),s(m+τ),s(m+2τ),s(m+3τ),…]
(1)
式中,y(m)为重构后的相空间矢量,s(m)为对应维数的矢量,τ为延迟时间,m为已知变量(在本文中为系统状态参数p)。
延迟时间构成了相空间的采样间隔,是相空间重建的重要参数。选择的延迟时间若过大,会导致时间序列中任意2个相邻的延时坐标点失去相关性,不能反映重构动力系统的特性;选择的延迟时间若过小,则会导致相邻延时坐标点过于接近而无法相互独立,产生数据冗余。
为保持相空间重建过程中各个分量相对独立,可以采用自相关函数来确定理想的延迟时间。自相关函数能够保证信号本身与其延时坐标点之间的度量处于冗余与不相关之间。自相关函数C初次出现零点时的值就是需要达到的正确的延迟时间[17]:
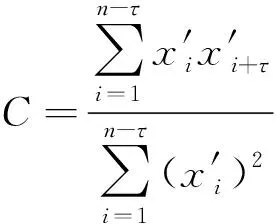
(2)
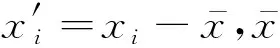
极限环来自于控制理论中非线性系统的概念。在非线性系统中,将系统状态中的参数坐标点与该参数的时间导数坐标点构成的坐标平面称为“相平面”;在二维相平面上,该系统状态中的参数随着时间变化,形成一条曲线,称为“相轨迹”。在三维相空间中,任一极限环表现为一条孤立封闭的相轨迹;当时间趋于无穷,若附近所有相轨迹都趋于同一极限环,则该极限环为稳定极限环。在热声耦合振荡系统中,稳定极限环表现为周期固定、等幅度的自激振荡,任何微扰动都会使系统回到极限环中。图9~11为采集的系统状态参数p与其时间导数所构成的三维相空间,以红色线条表示相轨迹。
稳定极限环表明热声耦合振荡系统为周期固定、等幅度的自激振荡;但实验过程中存在噪声影响,在图9(a)~(c)和图10(d)中,极限环为封闭圆环,其代表着400.0 Hz左右的振荡主频率以及实验过程中其他噪声的影响,表现为夹杂着噪声的周期性热声振荡。这也说明功率谱图中除主频率及其激起的二次谐波、回流区内低频振荡之外还存在其他噪声信号。

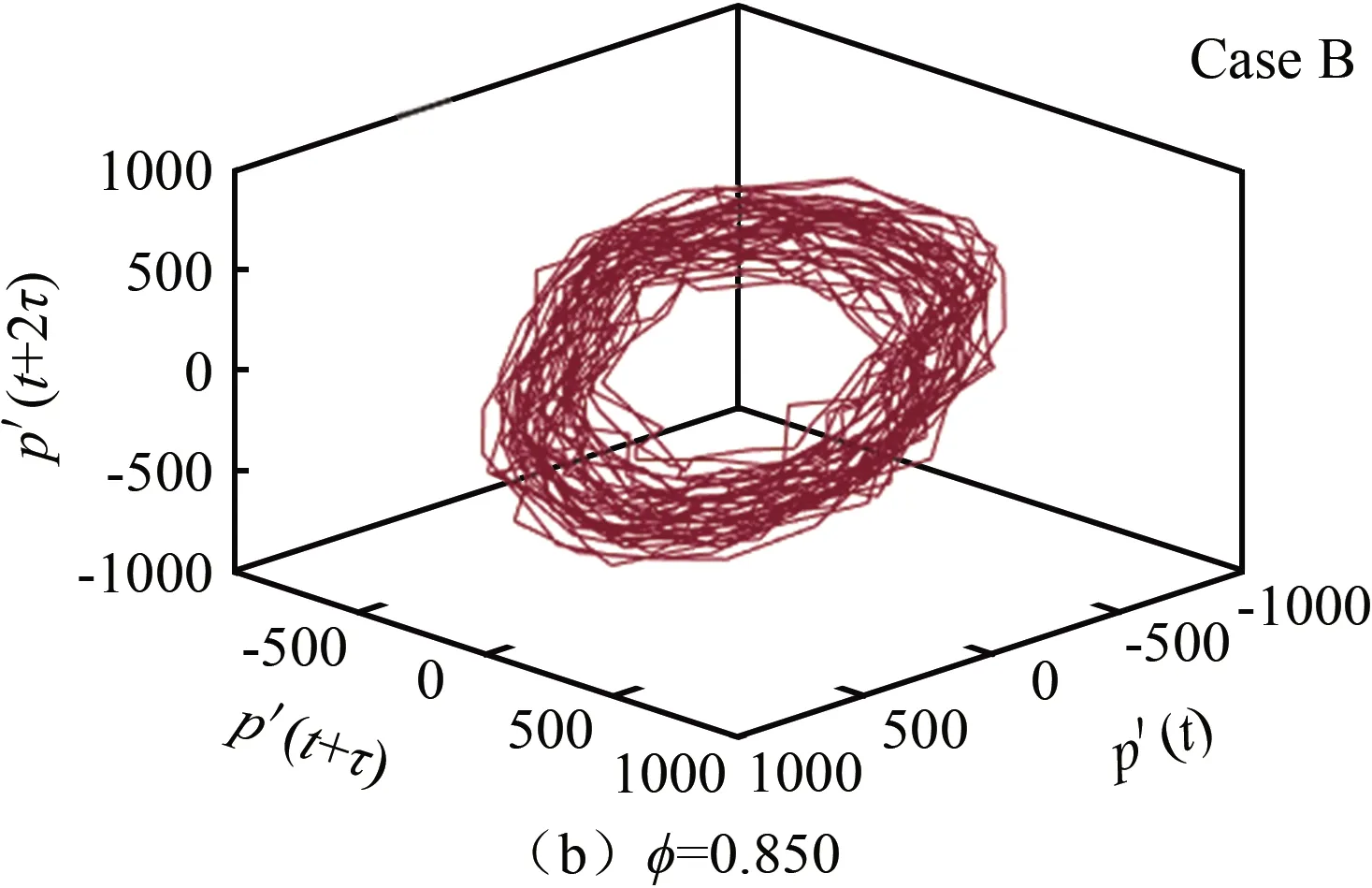

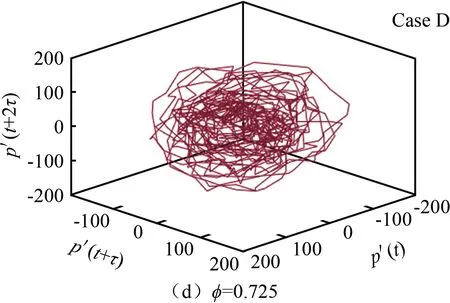
图9 当量比减小过程的相空间重构图Fig.9 Phase space reconstruction graph with equivalent ratio decreases
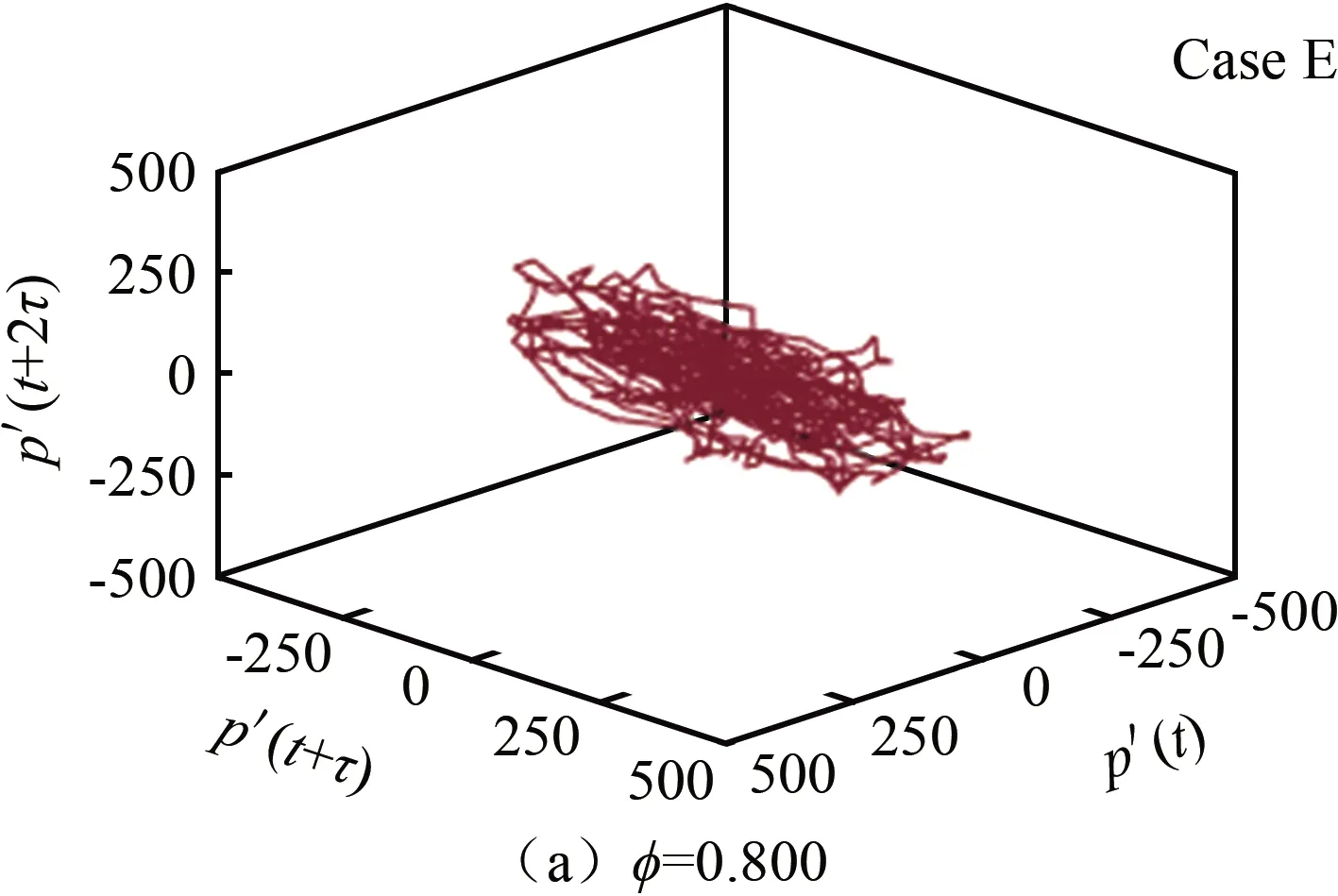
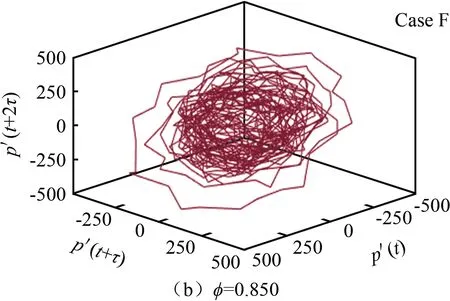


图10 当量比增大过程的相空间重构图Fig.10 Phase space reconstruction graph with equivalent ratio increases



图11 φ=0.850时内管体积流量变化下的相空间重构图Fig.11 Phase space reconstruction of inner pipe with volume flow rate change at φ=0.850
随着当量比减小,振荡减弱,振幅减小,圆环形逐渐向内聚集,空间坐标值也由1000变为500。越聚集,对应的状态越稳定;当V型火焰稳定燃烧时,相空间上的极限环已完全聚集为一团。当量比增大至φ=0.925时(如图10(d)所示),极限环又恢复为M型火焰对应的形态。
在“过程2”实验中,当量比固定为0.850,V型火焰持续至最终。图11(a)所示的极限环振荡表明,在最初的256.0 Hz主频振荡情况下,除其激起的二次谐波和回流区内频率外,还存在其他噪声信号。当内管的体积流量增大至2.8和31.0 L/min以及4.8和53 L/min时,燃烧振荡现象减弱很多,振幅减小,极限环向内聚集为一团杂乱的分布,燃烧趋于稳定。继续增大流量至5.5和62.0 L/min,出现了比稳定燃烧时面积更大的聚集区域(主频率为411.0 Hz),但尚未出现热声振荡特征,没有清晰的环形分布,如图11(d)所示。
国内的热声振荡研究涉及极限环振荡较少,且往往仅以文字说明,同时结合相关模型推理成因。本文采用先进的测量方法,依据Takenshas证明的构建多元相空间分析方法,引入自相关函数,将极限环振荡具象化,以图形结合热声振荡的模态转变进行分析对比。在热声耦合振荡系统中,稳定极限环表现为周期固定、等幅度的自激振荡,即使实验中存在噪声影响,也可以在图9(a)~(c)、图10(d)和图11(a)中呈现出封闭的圆环形状。而在稳定燃烧时,极限环在相空间内表现为混乱聚集的状态(相空间坐标平面的值代表振幅大小,可以表明振荡的剧烈程度)。图11(d)显示,相空间形态出现了比稳定燃烧时面积更大的极限环聚集区。
此外,本文研究所观察到的热声振荡现象与燃烧不稳定性中固有的非线性过程有关,因此,在实际系统中也可能存在混沌运动现象,可以采用极限环具象化方法结合混沌运动中的奇异吸引子理论来探究混沌系统中存在的形态规律问题。
4 结 论
为研究当量比、体积流量变化对自激非线性热声振荡和湍流火焰结构的影响,对一新型双旋流燃烧室开展了实验研究,得到如下结论:
1) 保持内外管甲烷流量不变,调整内外管空气流量:将当量比从0.900逐渐减小,燃烧由不稳定状态的M型火焰转变为稳定状态的V型火焰;随后再增大当量比至0.925,火焰又由V型转变为M型。但当量比两个变化方向的火焰转变临界点差别很大,呈现出非线性系统中特有的滞环现象,可能存在不稳定正反馈过程。
2) 保持内外管的当量比为0.850不变,调整内管的体积流量:在小流量时存在较强的热声振荡,增大流量后热声振荡现象明显减弱,燃烧变得稳定,火焰一直维持为V型火焰。
3) 通过对压力脉动信号的相空间重构分析,发现当振荡水平较高时,相空间重构图中呈现出明显的圆环形,与功率谱特性分析结果存在较明显关联。
4) 本文研究的双旋流燃烧室内热声振荡主频率分布于400.0和256.0 Hz左右。

