润湿异性表面液滴定向运动研究进展
曹 刚, 黄苏和, 李明升, 胡海豹,*
1. 西北工业大学 航海学院, 西安 710072; 2. 中国船舶工业系统工程研究院, 北京 100094
0 引 言
1805年,Young[1]首次提出了液滴在光滑固体表面的润湿理论,其后,Wenzel[2]、Cassie和Baxter[3]相继对该理论进行了完善,Furmidge[4]提出了倾斜固体表面液滴运动的临界角度方程,这些理论为固体表面的液滴定向运动研究奠定了坚实基础。目前,已有大量学者利用各种梯度表面驱动液滴运动,如表面张力梯度[5-6]、电荷密度梯度[7]、表面能梯度[8-9]等。此外,利用重力[10-11]、磁场[12-13]、光[14-15]等也可实现液滴在固体表面的运动。
润湿异性表面是一种典型的固体表面模型,其表面的液滴定向运动具有重要科研价值,在工业和日常生活中也发挥了重要作用(如水收集[16-18]、油水分离[19-21]、液滴调控[22-24]、质子交换膜燃料电池的自排水[25-26]等),已成为表界面领域的研究热点。Ju等[9]发现仙人掌表面具有定向水收集能力后,提出了可用于干旱地区植物供水的仿仙人掌表面模型,如图1(a)所示。Bai等[27]制备了15 min内收集1.3 mL水的仿仙人掌表面模型,其中单个仙人掌刺的水收集速率达0.3 μL/min;Tian等[28]受蜘蛛丝模型启发,制备了77 cm长的仿生空腔蜘蛛丝状微纤维网,在0.408 mL/min雾流时,可在2 min内收集0.36 mL水,如图1(b)所示;Li等[29]发现制备的仿生瓶子草表面沟槽结构具有更高的水收集效率。也有学者[17, 30-31]利用润湿异性的楔形表面进行水收集仿真与实验研究。此外,Li等[20]利用仿仙人掌刺锥形阵列表面实现了高达(98.9±0.4)%的油水分离效率,如图1(c)所示。Wang等[19]受蝴蝶翅膀表面启发制备的超疏水性铜网膜,可至少进行8次油水分离;受猪笼草启发,Li等[21]设计了可高效分离油水混合物的装置。另外,利用润湿异性表面的液滴运动可实现液滴的融合。Chen等[11]实现了超疏水表面Y形亲水条带上的液滴融合,如图1(d)所示;You等[32]开展了进一步研究,通过在超疏水表面Y形亲水条带交叉处制备亲水性方形区域(如图1(e)所示),可以捕获第一滴液滴,当第二滴液滴到达时可实现100%的混合效率,如图1(f)所示。






图1 润湿异性表面液滴定向运动的潜在应用Fig. 1 Potential application of directional movement of droplets on wetting heterogeneous surface
本文从楔形表面、沟槽阵列表面、亲水-疏水表面、非对称形貌表面和生物表面等角度,系统介绍润湿异性表面液滴定向运动的最新研究进展,展示国内外典型研究案例,并对未来研究工作的重点进行展望。
1 楔形表面的液滴定向运动
1.1 不同润湿异性楔形表面的液滴定向运动
2007年,Zhang等[33]在疏水表面制备了不同形状(梯形、矩形、三角形、新月形)的超亲水区域,实现了液滴在无外力条件下的水平运动或克服重力向上运动。此后,多位研究者[17, 34-38]也采用不同方式制备了不同润湿异性的楔形润湿梯度表面,如Deng等[37]在石墨板上制备了具有润湿梯度的楔形图案,并在高黏附表面实现了液滴的定向运动及融合(石墨板即使倒转放置也可实现),如图2(a)所示;Zheng等[38]通过在楔形疏水氧化铜表面涂覆PDMS(聚二甲基硅氧烷)油层,消除了液滴接触线钉扎,可实现液滴自驱动,如图2(b)所示(图中αw表示楔角);Luo等[31]制备了光滑液体注入的多孔楔形表面,对于不同PH值的液滴均可实现定向运动,如图2(c)所示。此外,还有学者[39-43]开展了相关仿真研究。



图2 不同形式的楔形表面液滴定向运动Fig. 2 Directional movement of droplets on wedge-shaped surface of different forms
尽管研究者已经实现了楔形表面的液滴定向运动,但液滴定向运动的位移、速度等更值得关注。Song等[34]发现,在超疏水-亲水楔形表面(即为超疏水包围的亲水楔形表面,在本节中此类概念类似),液滴的自运动比在超疏水-疏水和疏水-超亲水楔形表面更为有效;Wang等[43]发现楔形表面较大的润湿性差异有利于液滴运动;Luo等[31]利用液滴合并与追逐过程将其表面能转变为动能,实现了疏水楔形表面液滴长距离运动。
Deng等[37]发现,液滴在楔形表面的运动距离可通过楔角及液滴体积进行调节,但未给出定量分析。基于此,Liu等[44]发现,疏水-亲水楔形表面亲水区域的楔角越大,液滴定向运动位移越小;其瞬时运动速度随时间先增大后减小,与文献[40]结果一致。与Liu等[44]不同的是,Zhang等[33]发现,疏水-超亲水楔形表面液滴的平均速度随楔角的增大而增大,随液滴体积的增大而减小。
1.2 楔形表面液滴运动模型及相关研究
Sen等[45]在制备的超疏水-超亲水楔形表面发现不同黏度和表面张力的液滴运动具有3种不同的时间状态:(1)Washburn类型的缓慢扩展(X~T1/2,其中,X为无量纲前端液滴位置,T为无量纲时间);(2)快速的Laplace压力驱动扩展(X~T);(3)缓慢的、密度增加的Tanner型薄膜扩展(X~Ψ3/10T1/10,其中Ψ为密度比),如图3(a)所示。此后,Xu等[46]利用三维格子Boltzmann模型证实了Sen等的理论,如图3(b)所示。


图3 楔形表面液滴定向运动及其3种不同时间状态的实验与仿真Fig. 3 Experiment and Simulation of the directional movement of the droplet on the wedge-shaped surface and its three different time states
受空气环境中楔形表面液滴定向运动启发,Liu等[47]在铝板上制备的超亲水-超疏水楔形表面实现了液体环境中气泡在楔形超疏水表面的定向运动,即使将试件表面倾斜,气泡也可沿试件表面定向运动。Song等[48]将该结构进一步改造为连续的超亲水-超疏水楔形结构,实现了液体环境中气泡约80 mm的长距离运动。Xu等[42]利用分子动力学研究了不同楔角和润湿梯度的楔形表面液滴冷凝的最佳条件,发现楔角14°且疏水-亲水楔形表面液滴冷凝速率更高、排水能力更好。
2 沟槽阵列表面的液滴定向运动
在2010年之前,就有大量学者[49-52]开展了矩形沟槽阵列表面液滴运动研究。当液滴静置于沟槽阵列表面时,其沿垂直和平行于沟槽方向的接触角表现出明显的润湿异性。研究表明,液滴沿垂直于沟槽方向的接触角(记为CA⊥)比沿平行于沟槽方向的接触角(记为CA‖)更大[49, 53-61],如图4所示。有研究者[53, 55, 62-63]认为这是由于三相接触线的钉扎效应导致液滴沿垂直方向比沿平行方向有更大的能量障碍;而Wang等[54]认为这仅仅是由于液滴沿垂直和平行方向的能量障碍不同。对此,乔小溪等[64]认为:液滴沿平行于沟槽方向具有较小的运动阻力、易铺展,因此接触角较小;而在垂直于沟槽的方向上,由于沟槽的阻隔作用,接触角较大。

图4 各向异性润湿的定向测量原理图[59]Fig.4 Schematic of the directional measurement of anisotropic wetting [59]
除研究液滴在沟槽阵列表面的接触角外,研究者对液滴在沟槽阵列表面运动的滑动角也较为关注。研究发现:液滴沿垂直于沟槽方向的滑动角(记为SA⊥)大于平行于沟槽方向的滑动角(记为SA‖)[55-56, 60],如图4所示;当液滴体积逐渐增大时,其沿垂直和平行于沟槽方向的滑动角均逐渐减小,如图5(a)和(b)所示,这是由于随着液滴体积的增大,其重力在斜面上的分力逐渐增大,导致滑动角减小[55-56, 60-61]。

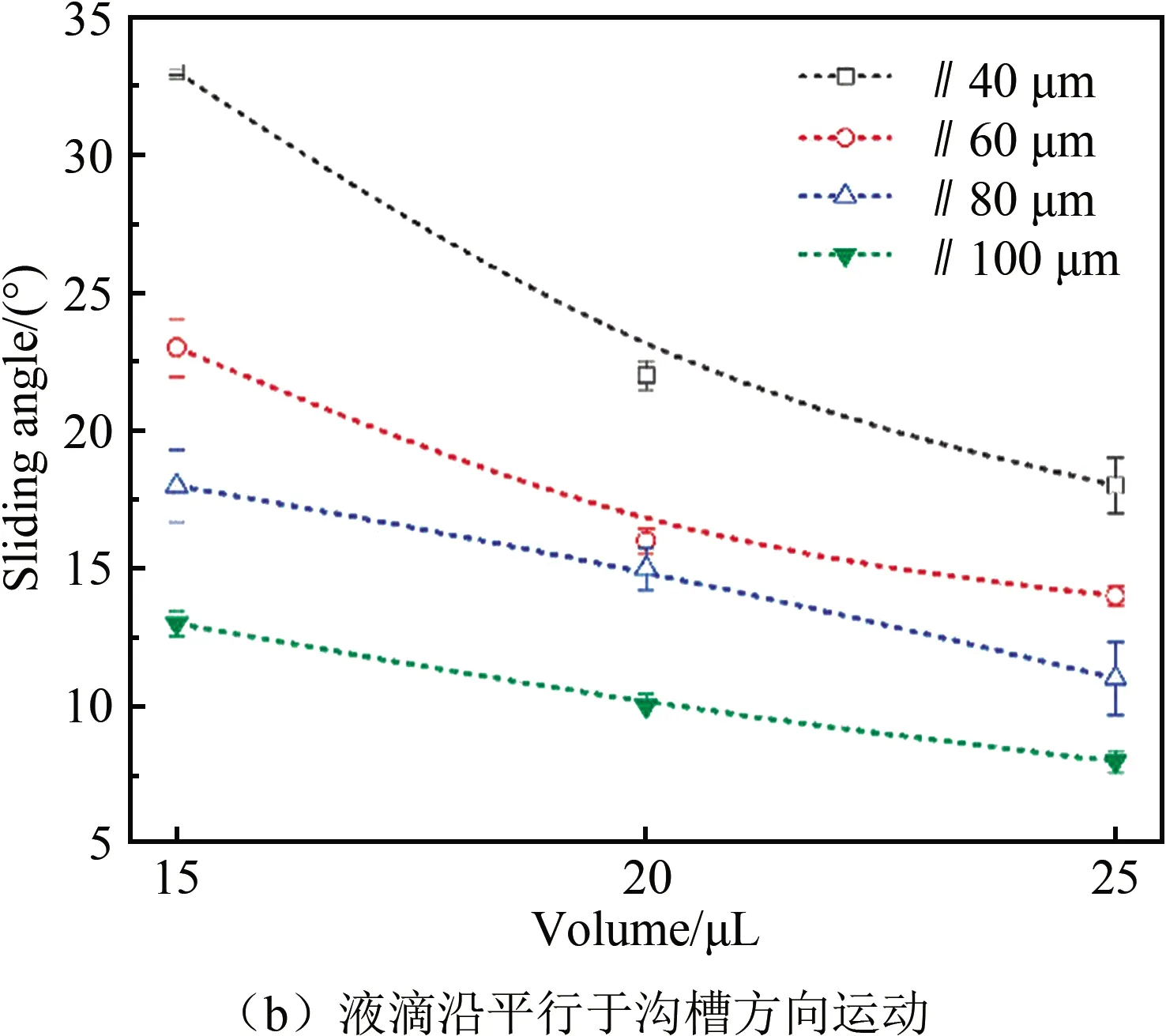
图5 液滴沿沟槽阵列(微柱宽度80 μm)表面运动的滑动角与液滴体积的关系[53]Fig. 5 Relationships between the sliding angle of a droplet moving along the surface of the groove(micropillar width 80 μm) and the droplet volume [53]
此外,部分学者[55, 59-61, 65]开展了两相邻沟槽间距对液滴滑动角的影响研究。Ding等[61]发现,沟槽阵列表面液滴运动的阻力主要由垂直于运动方向三相接触线的长度分量与表面张力的乘积决定,且三相接触线有效长度增加会阻碍液滴运动。Zhang等[60]发现,随沟槽宽度增大,液滴沿垂直和平行于沟槽方向的滑动角均逐渐减小,但垂直于沟槽方向的滑动角仍较大,如图6和7所示。而Lian等[59]发现,随两相邻沟槽之间微柱宽度增大,液滴沿2个方向的滑动角均逐渐增大,且当微柱宽度达到300 μm时,液滴黏附于试件表面不运动,而此时接触角呈明显的下降趋势,如图8所示。此外,部分学者[53, 55, 64, 66-67]还研究了沟槽宽度对液滴接触角的影响。

图6 液滴运动示意图(沟槽阵列表面倾斜10°)[60]Fig. 6 Schematic diagram of droplet movement(the surface of the groove array is inclined 10°) [60]

图7 液滴滑动角随沟槽宽度的变化[60]Fig.7 Change of droplet sliding angle with groove width[60]

图8 接触角与滑动角随两相邻沟槽之间微柱宽度的变化[59]Fig.8 Change of contact angles and sliding angles with the width of micropillars between two adjacent grooves[59]
对于液滴在沟槽阵列表面的运动机制,He等[53]发现液滴沿垂直于沟槽方向运动时,液滴的后退接触线在前进接触线开始运动后才运动,认为这可能是由于液滴处于亚稳态而引起的。Kumar等[55]的进一步研究表明,液滴沿平行于沟槽方向运动时,其前进接触线和后退接触线类似于在光滑表面运动,如图9(a)所示;而当液滴沿垂直于沟槽方向运动时,接触线呈“黏滑”运动状态,即液滴前进接触线在后退接触线脱离表面后开始运动,如图9(b)所示,或后退接触线在前进接触线脱离表面后开始运动,如图9(c)所示。而在上述研究工作之前,Lv等[68]仅发现当液滴在倾斜疏水方柱表面运动时,后退接触线先脱离方柱表面接触到下一个方柱(其间前进接触线保持不动),而后前进接触线才开始运动,如此往复。

图9 微沟槽阵列表面液滴运动示意图[55]Fig. 9 Schematic diagram of droplet movement on the surface of microgrooves [55]
以上关于沟槽阵列表面液滴前进接触线和后退接触线运动状态的研究,推进了液滴运动模型的建立。当液滴在倾斜固体表面运动时,Furmidge[4]提出了如下力平衡方程:
ρgVsinα=γLV(cosθr-cosθa)w
(1)
式中,ρ和V分别为液滴密度和体积;g为重力加速度;α为滑动角;γLV为气-液界面表面张力;θr和θa分别为液滴后退接触角和前进接触角;w为沿滑动方向的液滴宽度,可理解为液滴与固体表面接触的长度。如图9(d)所示,当液滴在沟槽阵列表面运动时,a为微柱宽度,P为1个沟槽加1个微柱的宽度,r1和r2分别为液滴在沟槽阵列表面的长轴半径和短轴半径。经适当简化,可得到液滴沿平行于沟槽方向运动的滑动角为[55]:

(2)
当液滴沿垂直于沟槽方向运动时,基于液滴与固体表面自由能变化模型,可得到其滑动角为[55]:

(3)
式中,θs为液滴在光滑表面的接触角。
He等[53]从液滴属性、重力等角度提出了液滴沿平行和垂直于沟槽方向的滑动角模型,其表达式为:

(4)
式中,Eadhesion为液滴与固体表面接触的单位面积黏附能,Scontact为液滴与固体表面的接触面积,G为液滴重力,COM为液滴质量中心。由于液滴沿垂直和平行于沟槽方向的黏附能不等,不同方向滑动角的差异主要是由液滴和固体表面单位接触面积的黏附能不同而引起。
3 亲水-疏水表面的液滴定向运动
3.1 润湿异性条带对液滴运动的影响
最早在2005年,Morita等[69]采用真空紫外光刻方式制备了亲水-疏水条带相间表面,发现液滴沿垂直于条带方向的静态和动态接触角均比沿平行于条带方向更大,这与Drelich等[70]的研究结果一致;但是,液滴沿平行于条带方向的滑动角比垂直于条带方向更小,其原因可能是液滴沿2个方向的能量障碍不同。2008年,Suzuki等[71]发现,对于水平倾斜角35°、侧向倾斜角13°的疏水-疏水条带(500 μm - 500 μm)相间表面(如图10(a)所示。图中,α、φ、β分别表示水平倾斜角、侧向倾斜角、液滴运动方向与重力在试件表面的投影方向所形成的偏角),液滴质量越小,其运动方向与重力在试件表面的投影方向所形成的偏角越大,而这种运动行为依赖于液滴尺寸和侧向倾斜角。与Suzuki等[71]的研究类似,Nakajima等[72]在疏水表面制备了不同大小的规则三角形亲水条带表面(如图10(b)所示),发现在水平倾斜角35°斜面上,当水滴从三角形顶点向底边运动时,其运动方向会向重力在斜面的投影方向右侧偏移(如图10(c)左图的左半部分所示),而当水滴从三角形底边向顶点运动时,偏移方向相反(如图10(c)左图的右半部分所示);当水滴被替换为乙烷液滴时,未观察到此现象(如图10(c)右图所示)。此外,部分学者[73-74]还对润湿异性条带相间表面的液滴运动进行了仿真研究。
在上述研究工作中,液滴都是利用外部力场运动。Bliznyuk等[6]采用光刻方式制备了亲水-疏水条带相间表面,通过不断增加亲水区域面积分数,产生足以驱动一定体积液滴运动的表面张力梯度,如图10(d)和(e)所示,图中wp-s表示全氟十二烷基三氯硅烷(PFDTS)构筑的蓝色疏水条带宽度与二氧化硅(SiO2)构筑的白色亲水条带宽度之比。这种润湿异性表面的有利之处在于:液滴更倾向于沿平行条带的方向运动,而垂直方向的运动则受到限制。之后,Wu等[5]设计了类似的超疏水-超亲水条带相间表面,液滴最大运动距离约7.32 mm,如图10(f)所示(图中,Δ表示自定义的润湿梯度,其值为橙色表示的超亲水条带面积增量与蓝色表示的超疏水条带面积之比)。
对于超疏水表面的单条超亲水条带,Chen等[11]的研究表明超亲水条带宽度对液滴润湿性有重要影响:随亲水条带宽度逐渐增大,液滴沿平行和垂直于条带方向的接触角均减小;液滴沿平行于条带方向的滑动角逐渐减小,而沿垂直于条带方向的滑动角逐渐增大。Zheng等[75]也进行了与Chen等[11]类似的实验,发现随超疏水表面单条疏水条带宽度增大,液滴沿平行于条带方向的接触角逐渐减小,而沿垂直于条带的接触角略有波动,如图11(a)所示。但是,随液滴体积增大,液滴沿2个方向的滑动角均减小;在相同的液滴体积下,沿平行或垂直于条带方向,疏水条带宽度越小,其对应的滑动角越小,如图11(b)所示。对此,Chen等[11]认为这种润湿异性源于液滴沿垂直和平行于条带方向不同的能量障碍,而Zheng等[75]则认为这是由亲水-疏水边界处的润湿性差异引起的。






图10 亲水-疏水条带相间表面液滴运动Fig. 10 Movement of droplets on the surface of hydrophilic-hydrophobic strips
此外,Xu等[10]也制备了与Zheng等[75]相似的润湿异性表面,发现在水平、侧向倾斜角皆为15°的超疏水表面上,疏水条带宽度越大,液滴运动的临界体积越大。这可能是由于条带越宽,液滴黏附力越大,而液滴体积增加产生的驱动力可以抵消黏附力[76]。Seo等[77]在超疏水表面的亲水条带上也发现了类似规律,这或许是由于亲水条带上的毛细力随条带宽度增大而线性增大[78]。
除上述研究工作外,Xu等[79]在超疏水表面制备了宽约200 μm的S形曲线条带,可通过调节试件表面倾斜角度和液滴尺寸,实现液滴沿超疏水表面的S形曲线条带运动,如图11(c)所示。然而,若液滴体积大于20 mL或试件水平倾斜角大于45°,液滴运动方向就不能被S形曲线条带所控制。Seo等[77]在超疏水表面制备了亲水条带,发现当液滴体积大于临界液滴体积时,液滴在亲水条带上能够呈球形作定向运动。Zhang等[80]在超疏水表面制备了多条亲水直线或曲线条带,发现当试件表面水平倾斜角10°时可实现液滴运动,甚至可实现水流运动,如图11(d)所示。You等[32]实现了液滴在超疏水表面亲水条带上的运动与融合。Yang等[81]发现,在超疏水表面的2条非平行亲水条带上,液滴更倾向于向条带变窄的方向(图11(e)和(f)中的A方向)运动。此外,Zhu等[82]利用超亲水表面2条非平行超疏水条带实现了液体环境中气泡的单向定向运动。






图11 超疏水表面润湿异性条带对液滴运动的影响Fig. 11 The effect of superhydrophobic surface wetting heterogeneous strip on droplet movement
3.2 液滴在超疏水表面的疏水条带上无质量损失运动
众所周知,液滴在亲水条带表面运动会有一定的质量损失;而在超疏水表面形成的疏水条带上,Hu等[83]发现了液滴的无质量损失定向运动,如图12(a3)所示。实验结果表明,液滴临界风速与条带宽度、沿条带方向液滴接触长度及表面润湿性等有关。之后,Xu等[10]利用超疏水表面的疏水条带实现了液流的连续定向运动而无质量损失,如图12(b)所示。此外,Huang等[84]采用由超疏水小孔和压力产生装置组成的移液管,实现了液滴无质量损失捕获、移动和释放。



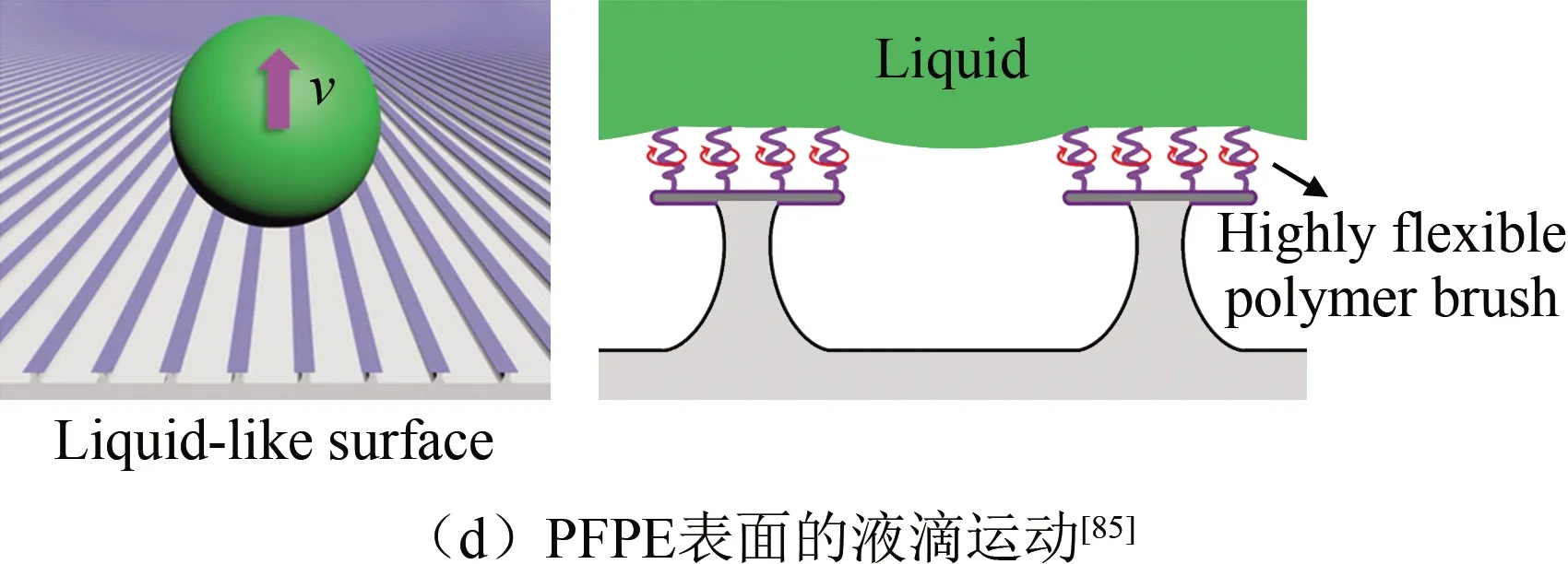
图12 液滴在超疏水表面的亲水或疏水条带上运动Fig. 12 The droplet moves along on a hydrophilic or hydrophobic track on a superhydrophobic surface
尽管研究者[10, 83-84]已经实现了宏观尺度的液滴无质量损失运动,但Huang等[85]发现微米尺度的液滴仍然会滞留在含氟聚合物的疏水条带上。他们认为传统的、低分子柔性的1H, 1H, 2H, 2H-全氟辛基三氯硅烷(PFOS)涂层表面无可移动的官能团,因此液滴在较小的临界运动速度下就会产生质量损失,如图12(c)所示;而具有高度柔性分子链的类液体全氟聚醚(PFPE)涂层表面具有较高流动性(由于非接枝到固体表面的PFPE链剩余部分可自由旋转或弯曲),有利于消除液滴运动过程中的质量损失。当液滴运动速度达到某临界速度(小于PFOS表面的临界速度)时,疏水表面的微观液滴无质量损失运动就会发生,如图12(d)所示。
4 非对称形貌表面的液滴定向运动
1999年,Sandre等[86]在石蜡表面制备了锯齿状非对称形貌的疏水表面微结构,并采用电润湿改变液滴接触角的方法,实现了液滴在非对称锯齿状表面的连续单向运动。此后,研究者对非对称表面的液滴操控开展了大量研究[87-99]。Buguin等[87]通过精密机加工、PDMS翻模制备的锯齿状非对称微结构,实现了电润湿状态下的液滴定向运动,如图13(a)所示;只振动时,液滴定向运动速度可达1 mm/s,如图13(b)所示。Shastry等[91]制备了一种新型微米立柱弧形图案(ARC)微通道结构(如图13(c)所示),当外加振动输入时,液滴沿轨道向弧形半径外侧方向运动(如图13(d)所示),最大速度为12.5 mm/s。Yeh等[99]制备了一种新型肩章状非对称微结构,可实现速度达23 mm/s的液滴单向运动,如图13(e)所示。Sun等[97]通过电润湿对弧形棘轮和肩章状非对称微结构(如图13(f)所示)实现了液滴定向运动及融合,如图13(g)所示。







图13 不同非对称微结构表面的液滴运动Fig.13 Transport of droplets on different asymmetric microstructures
此外,也有研究者开展了润湿梯度表面振动时的液滴运动[93, 95-96, 98, 100-102]及仿真研究[89, 103]。Feng等[93]在制备的梯度非对称润湿表面(如图14(a)所示)实现了振动时的液滴定向运动,如图14(b)所示。Geng等[89]采用分子动力学研究了振动作用下液滴在非对称疏水表面的定向运动,实现了2个液滴的融合,如图14(c)所示。



图14 振动表面液滴运动Fig. 14 Droplet movement on the vibrating surface
利用振动条件实现液滴在固体表面非对称基底上的定向运动具有很大的工程应用价值(如微流控芯片、生物实验和集水等[86-87, 89, 91-92, 102, 104-105]),吸引了大量研究者对非对称基底上的液滴操纵进行研究[88, 92, 104, 106-108]。Holmes[107]等研究了ARC基底设计对液滴运动速度的影响,并对运动速度进行了表征。研究发现振幅对运动速度有很大影响,且在一定范围内液滴运动速度随振幅的增大而增大,这与Duncombe等[109]的结论相同。Sun等[92]采用改进的电极布置方法,在非对称基底表面实现了仅用2条平行电极电润湿就使液滴产生定向运动,且15 μL的液滴运动速度可达13 mm/s。
在振动控制方面,Duncombe等[88]通过在疏水基底表面构造亲水弧形非对称结构,实现了以31 μm振幅驱动10 μL液滴作定向运动,降低了液滴运动所需的输入振幅。在液滴运动控制方面,Holmes等[108]通过改变轨道微结构的密度等参数,实现了液滴跨越轨道的选择性运动、融合和定时运动;Qi等[102]通过构造具有连续周期性化学梯度的表面,实现了水平振动作用下的液滴追赶与融合控制等。
许多学者对非对称基底上液滴定向运动的原理进行了研究[91, 98, 100-101, 109-114]。Duncombe等[109]发现润湿的非对称性主要体现在去润湿过程中前进接触线和后退接触线钉扎力的差异。在润湿过程中,液滴前缘的前进接触角小于后缘的前进接触角,而前缘的后退接触角小于后缘的后退接触角,且后退接触角的变化幅值比前进接触角的变化幅值更大,这与Shastry等[96]的结论相同。
Chamakos等[103]利用仿真对非对称界面运动液滴的机理进行了研究。液滴在非对称基底上的定向运动,主要是由于液滴三相接触线在非对称基底两侧受到的毛细力不同,且振动过程中液滴形态发生周期性变化,三相接触线在一定程度上随液滴形态的变化而移动(在作用力较弱一侧后移,在作用力较强一侧前移),最终实现液滴的定向运动,如图15(a)和(b)所示。




图15 不同条件下的液滴运动Fig. 15 Droplet movement under different conditions
Dong等[104]提出以紧凑模型描述液滴在弧形非对称基底上振动时的运动机理,认为非对称钉扎力是液滴运动的主要驱动力,同时还分析了液滴前进接触线和后退接触线在振动过程中的运动机理,认为外加振动使液滴在润湿与去润湿状态之间振荡(如图15(c)所示),弧形基底的作用使液滴前缘和后缘产生钉扎力差,在每个振动周期内,力的不平衡引起液滴定向运动,如图15(d)所示。
此外,针对亲水-疏水相间非对称弧形基底,Doucombe等[88]定义三相接触线前进和后退时钉扎力的差为滞后力FHys:
FHys=wγ(cosθr-cosθa)
(5)
式中,w为正交投影到钉扎方向的液滴宽度,γ为固-液表面张力。
当液滴置于试件上时,三相接触线所产生的滞后力通常位于亲水区域、疏水区域和亲水-疏水的边界区域,而三相接触线在亲水-疏水边界处的作用力占滞后力的主要部分。在非均质表面的表观接触角和三相接触线之间建立如下关系:
cosθapp=χ1cosθ1+χ2cosθ2+χbcosθb
(6)
式中,θapp、θ1、θ2和θb分别为液滴的表观接触角、亲水表面平衡接触角、疏水表面平衡接触角和亲水-疏水交界处的接触角,线分数χi为三相接触线长度在给定材料上或沿边界的正交投影到钉扎方向的比例(χ1+χ2+χb=1)。
假设当θb=θ1时三相接触线后退、当θb=θ2时三相接触线前移,由式(5)和(6)可得:
FHys=χbwγ(cosθ1-cosθ2)
(7)
当采用该非对称基底时,非对称的边界线阻力在液滴边界与轨道半弧形亲水-疏水界面边界间建立。假设与半圆基底完全重合的液滴边缘为前缘,不完全重合的边缘为后缘,由于非对称表面在振动作用下驱动液滴运动与接触线前缘和后缘的相对滞后有关,可通过液滴前缘和后缘之间的滞后力差FAniostropy来表征这种相对滞后:
FAniostropy=(χb, lead-χb, trail)wγ(cosθ1-cosθ2)
(8)
式中,χb, lead和χb, trail分别为液滴三相接触线的前缘接触线分数和后缘接触线分数。两者取决于液滴和轨道设计之间的相互关系,如:弧形周期、弧形图案宽度、轨道宽度等。由于边界的接触线分数难以测定,上式仅用于设计参考,不适用于准确计算。
5 生物表面的液滴定向运动
部分生物表面的结构特征可使液滴产生较强的润湿异性,如仙人掌刺、蜘蛛丝、蝴蝶翅膀、猪笼草口缘表面等[115]。2010年,Zheng等[8]发现“润湿重建”亲水性蜘蛛丝(Uloboruswalckenaerius)由周期性纺锤节和连接处组成(如图16(a)所示),其表面特征足以驱动一个5~20 μm的液滴从连接处到纺锤节作定向运动。之后,Ju等[9]发现仙人掌(Opuntiamicrodasys)刺表面的梯度沟槽(如图16(b)所示)也可以驱动液滴定向运动。2019年,Wan等[116]发现松针(Pinustabuliformis)表面(如图16(c)所示)可使液滴自运动约20 mm,实现了液滴沿松针表面沟槽自发从顶端向根部的定向运动。液滴在蜘蛛丝、仙人掌刺和松针表面之所以具有如此强大的定向运动能力,是因为其表面结构特征产生了驱动液滴定向运动的表面能梯度和Laplace压力梯度。

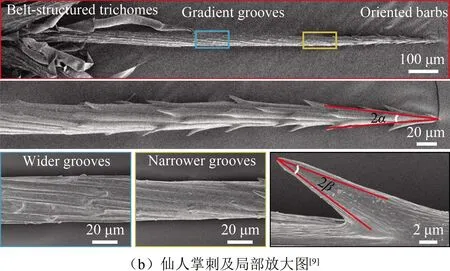

图16 生物表面微结构[8-9, 116]Fig. 16 Biological surface microstructure[8-9, 116]
2016年,Chen等[117]发现猪笼草(Nepenthesalata)“投手”口缘表面(如图17(a)所示)具有液滴定向运输能力。受猪笼草“投手”口缘表面结构特征启发,Li等[118]利用制备的仿生猪笼草“投手”口缘微结构弯管(如图17(b)所示)实现了液体在虹吸二极管内的定向运动。如图17(c)所示,若虹吸二极管“鸭嘴”空心部分朝下,则水池中的液体将克服重力沿弯管管壁向上运动,直至水池液体排尽,实现自虹吸;但当“鸭嘴”空心部分朝上时,则无法实现液体的自虹吸,如图17(d)所示。



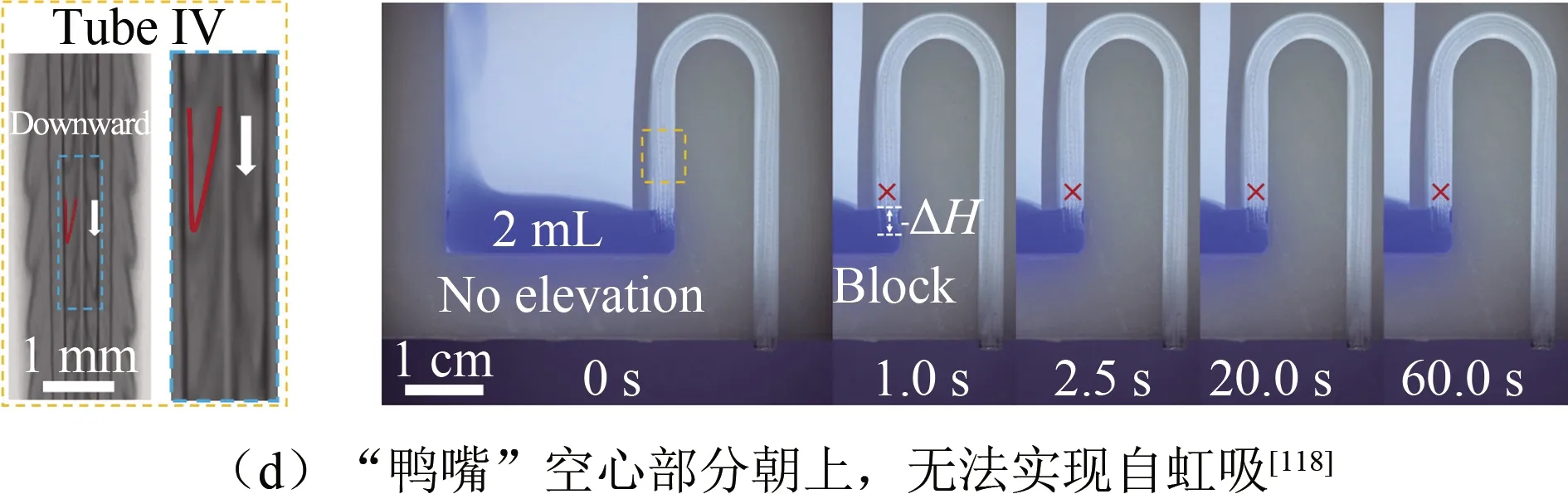
图17 猪笼草“投手”口缘表面微结构及其仿生Fig. 17 The microstructure of the peristome in the pitchers of Nepenthes alata and its related bionics
2018年,Chen等[119]发现瓶子草(Sarracenia)绒毛表面具有高低棱微纳分层结构(如图18(a)所示),可使液滴定向运动速度达(11 738±715) μm/s。受其启发,Li等[29]制备了仿生高低棱沟槽结构,在相同滑动角时液滴沿平行于沟槽方向运动,而沿垂直于沟槽方向运动一段距离后钉扎,如图18(b)所示。Kim等[120]受仙人掌刺的锥形结构与瓶子草绒毛表面的高低棱沟槽结构启发(如图18(c)的左、中图所示),制备了二者的复合微结构表面(如图18(c)的右图所示),显著提高了毛细压力,表现出优良的液滴定向能力(如图18(d)所示)和水收集能力(如图18(e)所示)。瓶子草绒毛表面液滴高速运动机理的发现,对于实现液滴高速导引行为的应用具有一定启发作用。


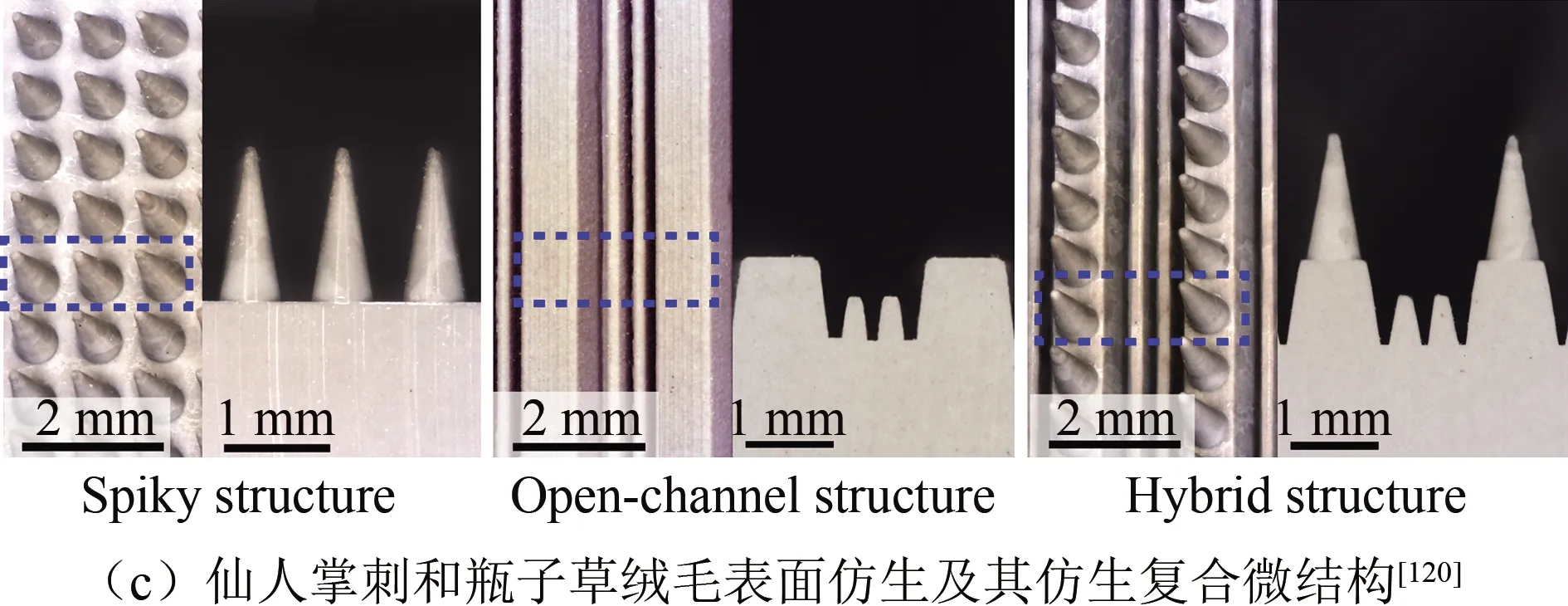


图18 瓶子草绒毛表面微结构及其仿生Fig. 18 The microstructure of Sarracenia trichome and its related bionics
此外,Parker等[121]观察到纳米布沙漠中的甲壳虫能够充分利用背部的蜡质疏水区域与非蜡质亲水区域捕获水滴;Nørgaard等[122]的研究表明,甲壳虫背部的水收集效率与其翅鞘结构类型、背部表面积的相关性很小。受甲壳虫背部结构启发,学者们[123-126]开展了大量相关仿生研究。
除以上研究外,Prakash等[127]发现水鸟以棘轮方式不断打开、闭合喙部,利用表面张力把包裹于液滴中的食物从喙部顶端运输至喙内。许多学者[128-136]对荷叶、玫瑰花瓣、美人蕉叶、水稻叶、蝉翼、槐叶萍等生物表面的微观结构及其润湿性进行了研究,并开展了相关仿生研究。
6 总结与展望
润湿异性表面液滴定向运动在工程领域有着广泛的应用价值,是表界面领域的研究热点,相关研究有利于深入理解固-液相互作用机制,开发高性能的润湿异性表面。本文主要介绍了国内外学者在楔形表面、沟槽阵列表面、亲水-疏水表面、非对称形貌表面及生物表面等润湿异性表面液滴定向运动的最新研究进展,展示了国内外典型研究案例。探索润湿异性表面液滴定向运动及其机制具有重要意义,目前仍然有不少问题亟待深入探索:
1) 某些润湿异性表面(如楔形表面)可以实现液滴定向运动,但大多数情况下,液滴定向运动仍需外力(如重力)才可实现,还需研究者共同努力开发各种形式的润湿异性表面,实现液滴自驱动。
2) 国内外学者主要采用化学法、掩模法、激光加工法、微铣削法等单一或多种组合方法制备润湿异性表面,工艺复杂、精度低、不易大面积制备,还需进一步探索简单方便、适用性广,可大面积制备润湿异性表面的方法。
3) 目前,液滴在润湿异性表面实现定向运动的临界滑动角较大,在某些自驱动润湿异性表面运动的距离短、速度小,对某些潜在的微观尺度运动机制仍不清楚,还需开展进一步研究。
综上,在未来的研究工作中,可以从探索液滴运动机制的角度出发,制备优良的润湿异性表面,并实现液滴较小滑动角下的运动甚至自驱动;而在已能自驱动的润湿异性表面,实现液滴以更高的速度长距离运动。

