航发叶片铣削弹性变形量预测与工艺参数优化*

李许庆 石 艳 胥 云 廖映华 皮 浩

(四川轻化工大学机械工程学院，四川 宜宾 644000)

航空发动机叶片结构扭曲、厚度薄，最小前后缘半径为0.06 mm，且叶型轮廓公差须控制在±0.05 mm内，加工过程中极易产生变形问题，导致叶片质量不合格[1]。目前，叶片广泛采用高温合金、钛合金等难加工材料，大量研究表明，加工这类材料铣削力大和发热量高，易使叶片局部产生变形误差[2-3]。因此，研究铣削力和发热引起变形的控制方法对于提高叶片加工精度至关重要。

为能够有效地改善叶片铣削时产生的局部变形问题，国内外学者进行了诸多研究。王凌云等[4]联合使用AdvantEdge和ANSYS完成了叶轮弹性变形量预测；黄涛等[5]通过理论分析和实验建立刀具-工件切削变形模型，得到控制叶片变形的较优刀轴倾角；李忠群等[6]利用力学和有限元法对航空机匣进行了加工变形量预测与参数优化；杨帆等[7]建立了叶轮加工效率-加工成本-加工质量优化模型，实验表明效率提高24.1%；Zuperl U等[8]利用神经网络对切削力数据集进行训练，结果表明预测精度可达98%。

以上研究对叶片类零件铣削变形控制及参数优化提供了方法。但目前大部分文献集中在铣削力或铣削温度机理研究，对于铣削力和发热共同造成叶片变形的探究相对较少，缺少仿真模型和数据对叶片铣削参数优化。

故本文选择叶片半精铣型面工序所用工艺参数展开探究，构建叶片受热-力两因素引起的弹性变形模型，提取刀具-叶片接触点(刀触点)，添加热-力载荷在叶片刀触点获取变形量数据，采用BP神经网络对变形量数据进行训练和预测，结合遗传算法求取最优解，完成“模型构建-变形量预测-参数优化”叶片弹性变形控制方案。

1 叶片铣削弹性变形模型构建

1.1 铣削热-力模型

叶片榫头、叶缘和型面加工精度要求相对高，位置分布如图1。其中，叶片型面半精铣时铣削力和发热大，获取该工序铣削力和发热量是探究叶片弹性变形量预测与优化的开始。

截取刀具和叶片有效接触部分作为铣削模型，采用半径R=5 mm的WC基硬质合金球头铣刀，模型工件尺寸为10 mm×8 mm×3 mm，叶片材料为TC4钛合金，主要性能参数见表1。

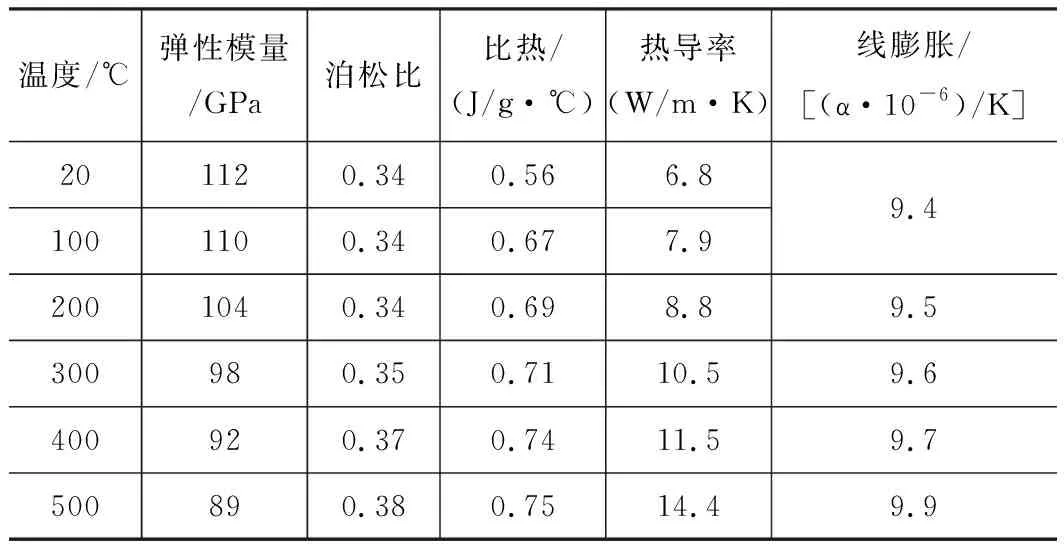
表1 TC4主要性能参数[9]

金属材料在实际切削中处于高温、大变形和大应变率的情况，通用有限元软件在模拟过程中常出现不收敛，难以获取可用物理数据。故利用Deform模拟刀具铣削工件，以获取三向铣削力(Fx、Fy和Fz)和工件温度数据。

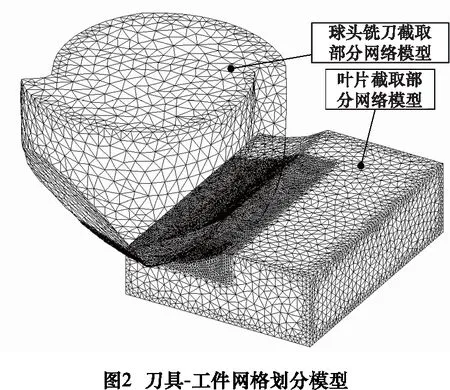
网格质量对于仿真结果的影响较大，Deform网格自动重划分功能使计算易收敛且数据精度更高。对刀具和工件网格划分后的单元数分别为36 317和83 043，模型如图2。

1.2 叶片弹性变形模型

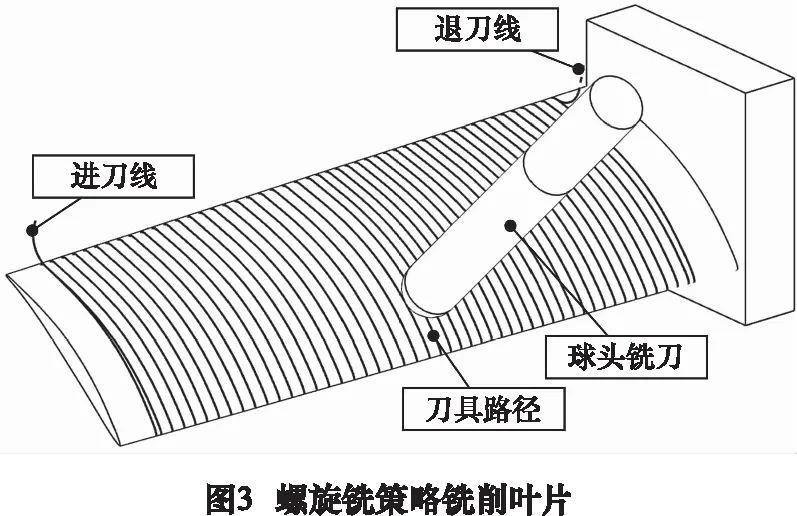
叶片型面半精铣常采用螺旋铣策略，如图3。由文献[5]可知，最大弯扭变形位于叶身高度0.6倍附近。故选用叶身中段的一条刀具路径并取32个刀触点，编号见图4，将载荷数据施加于此刀触点，模拟刀具铣削叶片过程。

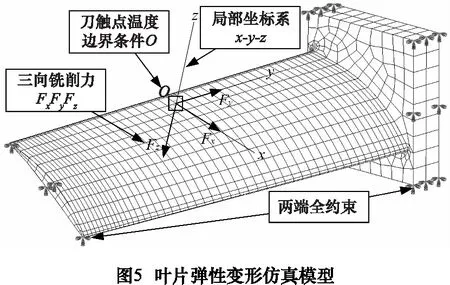
基于ABAQUS平台计算叶片弹性变形值。以刀触点为原点建立局部坐标系，该坐标系x轴正向为刀具进给方向，z轴正向为接触点曲面法矢，y轴根据笛卡尔坐标系确定。通过载荷方式添加三向铣削力于局部坐标系x-y-z方向，施加温度边界条件于O点，装夹方式两端全约束，网格类型选用热力耦合，如图5。

叶片加工过程中金属表面与环境之间存在温度差，采用自然对流换热描述叶片与环境的热交换，对流换热表达式(1)为：

q=h·(θs-θb)

(1)

式中：q为两介质间热通量；h为对流换热系数；θs为金属表面温度；θb为环境温度。本文对流换热系数取15 W/(m2·K)，环境温度设置固定值20 ℃。

2 数值计算与试验方案设计

2.1 叶片弹性变形量数值计算

试验因素选择轴向切深ap、主轴转速n、每次进给量fz和切削宽度ae，工艺参数值选用ap=1 mm，n=2 500 r/min，fz=0.4 mm/z，ae=1.2 mm，计算后获得刀触点处的三向铣削力为Fx=118.59 N，Fy=149.79 N，Fz=127.15 N，工件温度T=341 ℃。将该数据施加于各刀触点局部坐标系O-x-y-z，模拟后输出节点合位移量，如图6。

由图6可发现，一次半精铣螺旋走刀过程中叶片弹性变形规律呈现出“W”型，5号刀触点节点合位移量最小(U5=0.081 861 5 mm)；29号刀触点节点合位移量最大(U29=0.220 153 mm)，数据显示叶片进排气边相对于背气道和内气道弧面中部更容易产生弹性变形，分析结果与文献[10]一致。

为进一步探究叶片弹性变形量最大值发生位置，完成一次螺旋走刀后冷却10 s，后处理输出合位移云图，如图7。

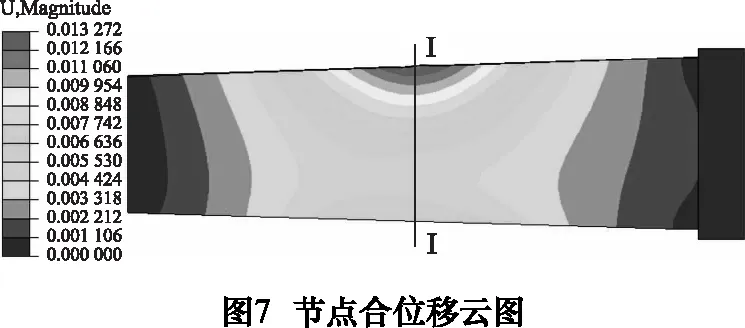
图7中，叶片节点合位移量在Ⅰ-Ⅰ方向表现为“两边大中间小”，分析原因：叶片两端为全约束装夹方式，位移为零，而进排气边处于悬空位置，且叶缘弧边厚度相对于中部位置厚度较小，受三向铣削力和发热影响，发生弹性变形。

根据数值模拟结果，半精铣叶身1/2处进排气道附近刀触点位置更容易产生变形，与文献[5]、文献[10]结论一致。故选取29号刀触点的节点合位移量U作为叶片弹性变形量研究值。

2.2 试验方案设计及结果

对叶片弹性变形量进行预测，需要进行多组试验以获取数据集。中心复合设计(CCD)能够设计出具有代表性的正交试验组合方案，如表2。

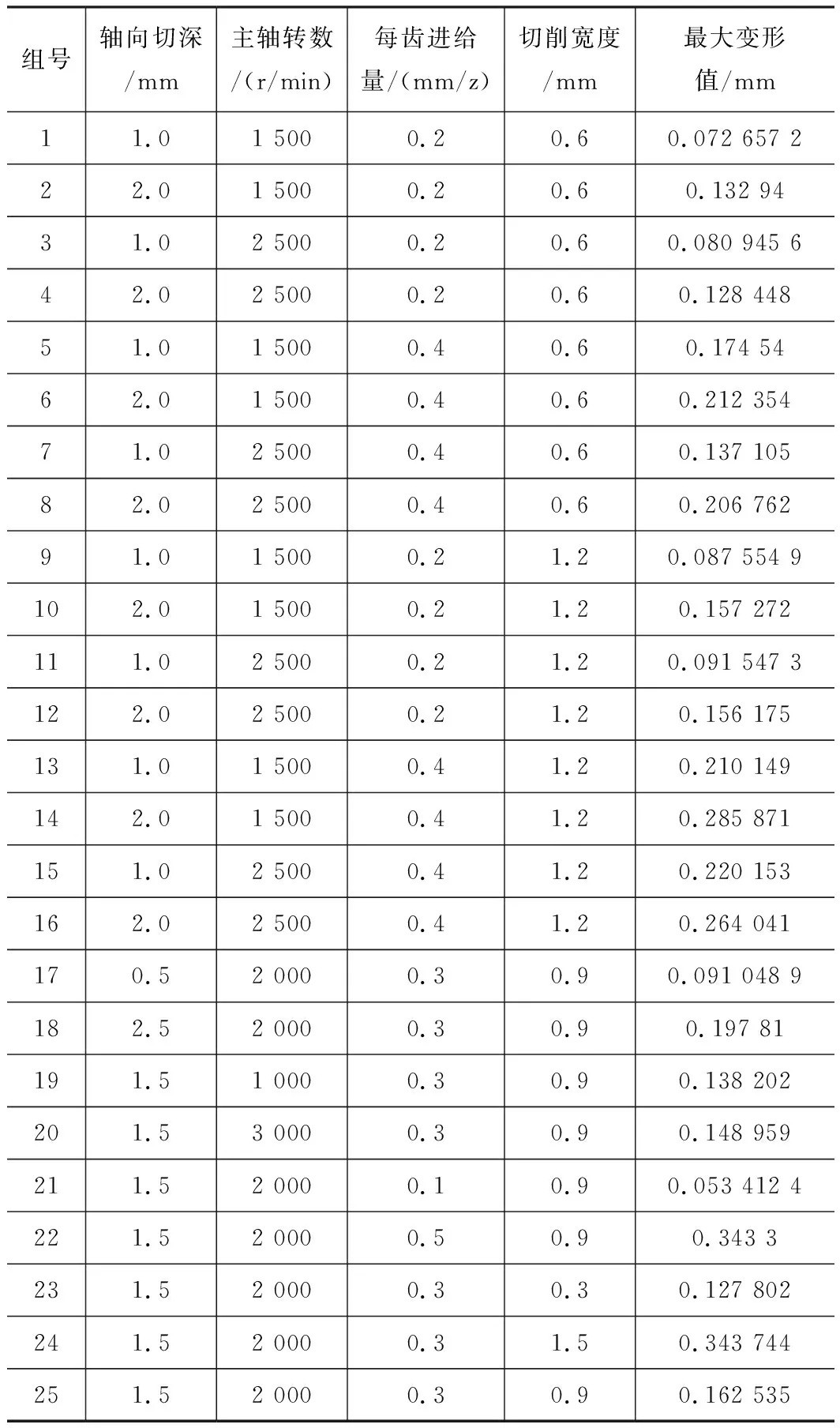
表2 CCD正交试验方案及结果

表2所有方案组，计算后的最小变形量值为0.053 412 4 mm，最大值达0.343 744 mm，均超出叶片型面公差范围，所以需要对工艺参数组进行优化。

3 BP神经网络预测叶片弹性变形量

3.1 神经网络模型建立

BP神经网络预测模型包含输入层、隐含层和输出层，各层神经元通过权值和阈值连接[11]。本文采用3层网络模型描述输入输出之间函数映射，输入层4个神经元分别为轴向切深、主轴转速、每次进给量和切削宽度，叶片弹性变形量作为输出层神经元，隐含层结合式(2)调试，确定神经元个数为9。故神经网络结构为4-9-1，如图8。

(2)

式中：M为隐含层神经元个数；m和n分别为输出层和输入层神经元个数；a是[0,10]的常数。

3.2 预测模型训练

本文采用MATLAB对神经网络进行训练。由于输出值始终为正，隐含层选用Log-sigmoid函数，输出层采用purelin线性函数作为神经元传递函数，见式(3)和式(4)：

(3)

purelin(n)=n

(4)

式中：n为前一层神经元传入数据。

利用CCD方案获取的25组数据对神经网络进行训练，由于训练数据较少，将25组数据全部作为训练集，从中随机选取5组作为测试集。网络训练前需要对数据进行归一化，调用mapminmax( )函数将训练数据和测试数据归一化，函数式(5)为：

(5)

式中：x为样本数据；x*为归一化后的数值；xmax和xmin分别为样本数据中的最大值和最小值。

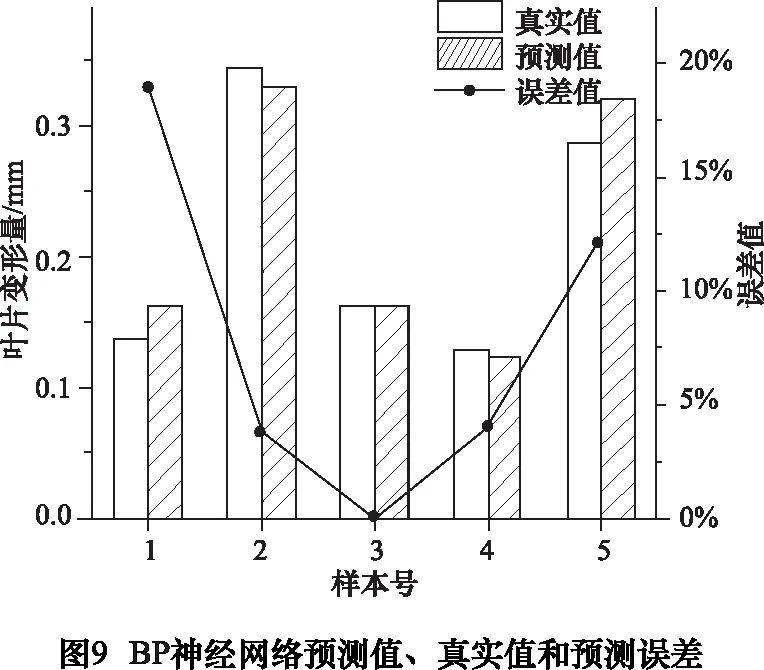
训练网络迭代次数为100，学习率为0.001，mse均方根误差目标值为1.2×10-6，其余参数采用默认值。SCG算法对于函数逼近有较好性能表现，故采用trainscg进行训练。调用sim( )函数对测试集进行预测，并将预测值反归一化。BP神经网络预测值、真实值和误差如图9。

由图9可知，测试集里BP神经网络预测值和真实值重合效果较好；另外，测试组最大预测误差小于20%，计算5组样本平均误差为5%，网络训练效果良好。

4 遗传算法优化与验证

为有效控制叶片型面局部弹性变形，引入遗传算法对训练好的BP神经网络进行迭代求解，以获取最小合位移量对应的工艺参数组合，BP-GA算法流程如图10。

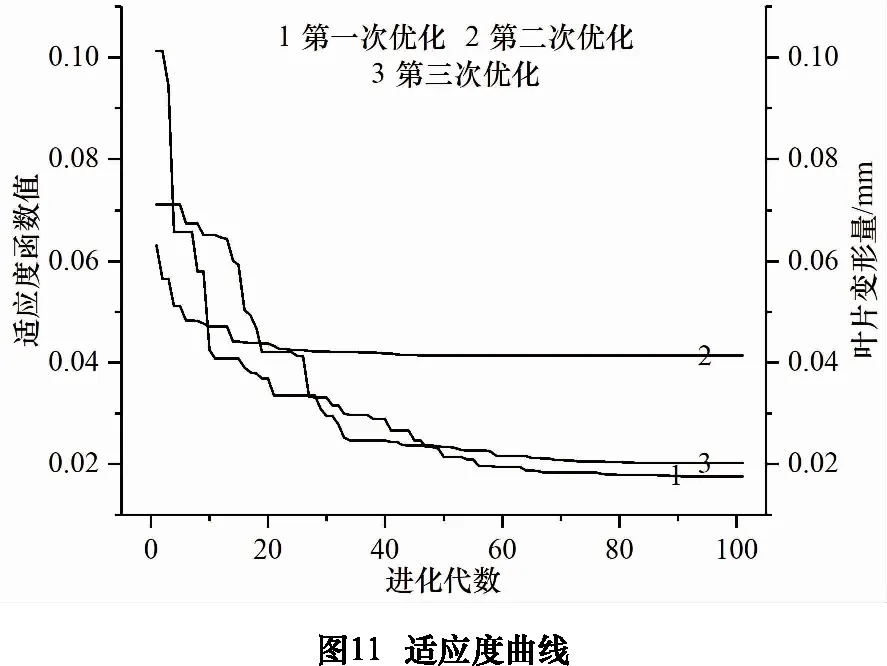
叶片弹性变形量需精确到小数点后6位，故染色体采用浮点数编码，种群染色体选择方法采用轮盘赌方式，初始种群规模为15，交叉概率为0.6，变异率为0.09，4个染色体数据范围分别为[0.5，2.5]、[1 000，3 000]、[0.1，0.5]和[0.3，1.5]，调用训练好的BP神经网络预测模型作为适应度函数。对该算法重复3次求解，100次迭代后适应度函数处于稳定值，如图11。

图11中，1、2和3适应度函数值随着进化代数的增加寻找到优选工艺参数组；另外，遗传算法寻优搜索过程中存在随机性，所以每次优化结果不同，但适应度值已满足叶片变形公差。

验证预测与优化数据的可行性，将优化的3组工艺参数代回有限元仿真模型，优化数据和仿真结果见表3。

表3 算法优化值和仿真验证值

表3中，算法优化值与仿真验证值平均误差为48%，这是因为叶片加工精度要求高，预测难度大；另外，对Deform输出量进行数据处理时，取值存在误差，故出现差异。但仿真验证值已满足叶片型面轮廓公差±0.05 mm，所以该参数是可行的。

5 结语

本文联合应用Deform和ABAQUS获取模型物理数据，利用BP-GA算法对叶片弹性变形量预测和工艺参数优化，结论如下：

(1) 该数值模型验证了最大弹性变形量发生于叶身中段叶缘处，并且能够有效预测弹性变形值，测试集平均误差为5%，可用于同类叶片变形量数据获取的相关研究。

(2) BP神经网络对于叶片半精铣弹性变形量的预测效果表现良好，GA算法能够搜索优选工艺参数组，且满足叶片变形公差±0.05 mm。结果表明，BP-GA算法用于该类叶片选择工艺参数是快速、有效和可行的。