基于能量平衡原理的机床结构动态优化
刘 江 王兆涛 阮业康
(①北京科技大学机械工程学院,北京 100083;②中船重工武汉船用机械有限责任公司,湖北 武汉 430084)
高速加工机床作为现代车间柔性化生产的基本单元,不仅具有较高的生产效率和加工精度,还具备快速响应、快速移动的特点,因此,为其设计轻质量、低惯量及高刚性的部件就显得十分重要[1]。
要保证高速加工机床在高速加工的过程中具有很高的加工精度,就必须保证其具有很好的动态特性。传统的机床结构设计方法是一种基于技术和经验积累的设计方法,虽然减少了机床设计阶段的工作量,但是机床无法获得较好的动态特性[2]。因此,在机床的设计过程中必须对机床部件进行动态性能优化设计。
找到机床结构上的薄弱区域的位置是动态性能优化设计的前提,现有的方法主要是通过振型动画判断出薄弱区域的位置。优点是可以通过有限元软件直观地观察出零部件的振动形态,而缺点是无法准确找到薄弱区域位置,使优化设计过程具有一定的盲目性。
能量平衡原理主要考察结构振动时候的势能和动能的分布情况[3]。动能分布集中的地方,其相对质量过大,应该减少该部分的质量;弹性势能分布集中的地方,其相对刚度较低,应增加该部分的局部刚度。该方法的优点是能够从能量分布云图准确地找到薄弱位置进行改进,缺点是能量是标量,无法从能量分布情况了解振动的形态。
本文提出以能量平衡为主、振型分析为辅,通过提高机床部件能量分布的均匀性来提高机床动态性能的方法,以数控雕铣机龙门架动态优化设计为例阐述这一方法的具体内容。
1 能量的有限元计算及均匀度评价参数
1.1 有限元能量计算
能量计算首先要得到系统的模态参数(固有频率及振型)。对于n自由度无阻尼线性系统,其振动方程为[4]:
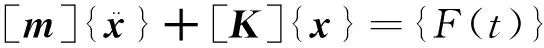
(1)
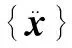
在得到了系统的固有频率及振型后,从中选择危险模态,接着分别计算这几阶危险模态的能量分布。
可以将机床结构件看作一个无阻尼振动系统,则其振动的能量主要表现为动能和势能。在有限元模态分析中将所有非线性问题转化为线性问题求解,单元的动能和势能计算表达式分别为[5]:

(2)
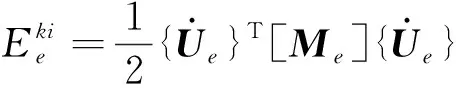
(3)
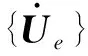
从式(2)~(3)可以看出,在振型不变的情况下,单元的动能和势能分别与单元的质量和刚度成正比。利用有限元软件计算出每个单元的动能和势能值并以云图的形式显示出来,这样能量集中的区域就可以很直观地观察出,其中动能分布较为集中的区域说明该区域的相对质量较大,需要减去质量。势能分布较集中的区域说明其相对刚度较差,需要增强局部刚度。
1.2 能量均匀度评价参数
如何判断系统能量分布的均匀程度,需要借用标准差。在统计学中标准差常被用作统计分布程度上的测量,它反映组内个体间的离散程度,其数值越大,说明大部分数值与平均值相差较大;数值越小,说明这些数值较接近平均值。因此可以使用标准差作为评价优化前后能量分布均匀性的指标。
对于机床势能的标准差,可以用以下公式计算[6]:
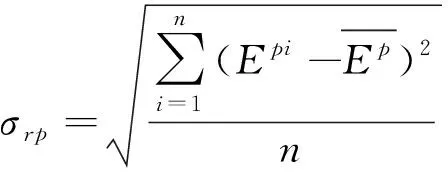
(4)
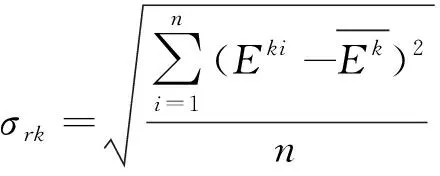
(5)
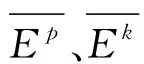
2 能量平衡原理动态优化的应用实例
本文以数控雕铣机龙门架的动态优化为例,对这一方法做具体阐述。
2.1 数控雕铣机龙门架的有限元模型
采用三维造型软件(如Creo)对龙门架进行实体建模。为了提高有限元模型精度,简化龙门架上面的小孔、小凸台和小倒角[7]。将处理后的模型导入有限元软件Ansys Workbench。设定网格大小为30,并在龙门架与床身的结合面上添加全位移约束,得到的有限元模型见图1。

2.2 龙门架的模态分析
实际中,机床低阶的几阶模态才有可能与激励频率重合或接近[8]。高阶的模态已经超过了激振力的频率,且阶数越高,对机床的影响就越小。研究龙门架的前六阶模态,得到其前六阶模态的频率和振型见表1。
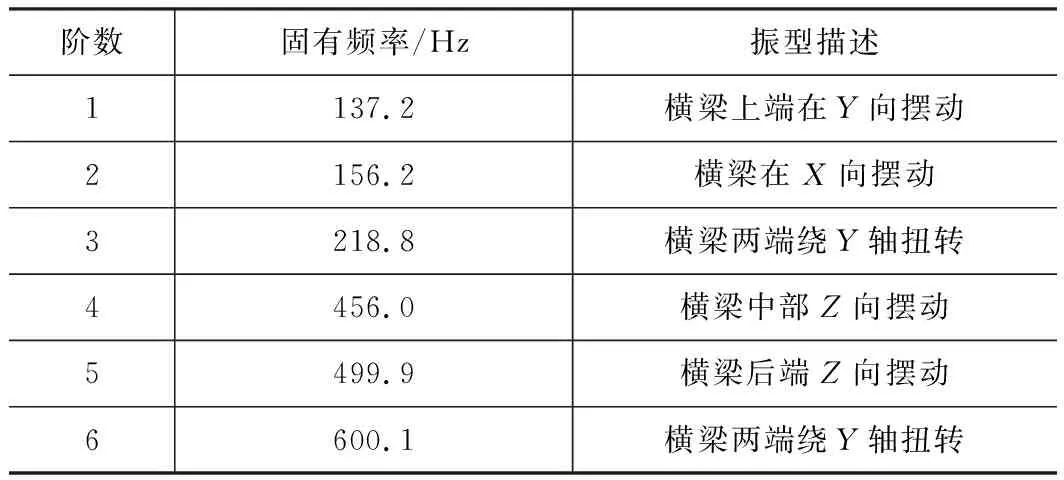
表1 龙门架前六阶固有频率及振型
从图2可以看出,第五阶的最大变形出现在横梁部位的后端,但此处的变形并不影响机床精度,因此属于安全振型。其余各阶均在横梁前端安放线轨的位置处发生较大变形,而线轨的安装精度直接影响着机床的加工精度,因此属于危险振型。可以得出结论:优化的时候可以不考虑第五阶模态,重点分析其他几阶。

2.3 龙门架的能量计算
在Ansys Workbench 中导出得到的龙门架模态分析结果,保存为.dat文件,然后在Ansys中读取该文件,利用Ansys的后处理功能显示出各阶的势能、动能的分布,结果见图3。


2.4 龙门架薄弱环节分析和优化
势能方面:从图3可以看出,第一、二、三阶势能主要集中在支腿外侧加强筋、支腿底面安装孔旁及支腿减重孔周围。说明这些部位的相对刚度不足,需要加强刚度。

动能方面:从图4可以看出,第一、二、三阶动能主要集中在横梁的后端,可以考虑去除该处的质量。第四阶的动能集中在横梁前端的中部,然而这一位置对龙门架的静刚度有较大影响,因此并不建议减小该处质量。第六阶的动能集中在横梁前面两端,考虑龙门架的美观性及方便铸造,该处也不予以修改。
综合能量平衡原理及工程实际,最终修改后的龙门架如图5所示。
该龙门架有以下4点修改:
(1)将支腿外侧加强筋的厚度由原来的20 mm增加到30 mm。
(2)支腿上的减重孔由140 mm×70 mm减小为120 mm×60 mm。
(3)底面安装孔处的厚度由原来的20 mm增加至30 mm。
(4)横梁后部切去了一个60 mm×100 mm的直角。

3 改进后龙门架的动态特性
用同样的方法对改进后的龙门架进行模态分析及能量分析,使用能量分布的标准差来比较改进前后的龙门架能量分布的变化。各阶单元能量的标准差值,见表2~3。从表2~3中看出各阶的动能和势能的标准差都有不同程度的降低,这说明改进后的龙门架能量分布相比之前更加均匀。
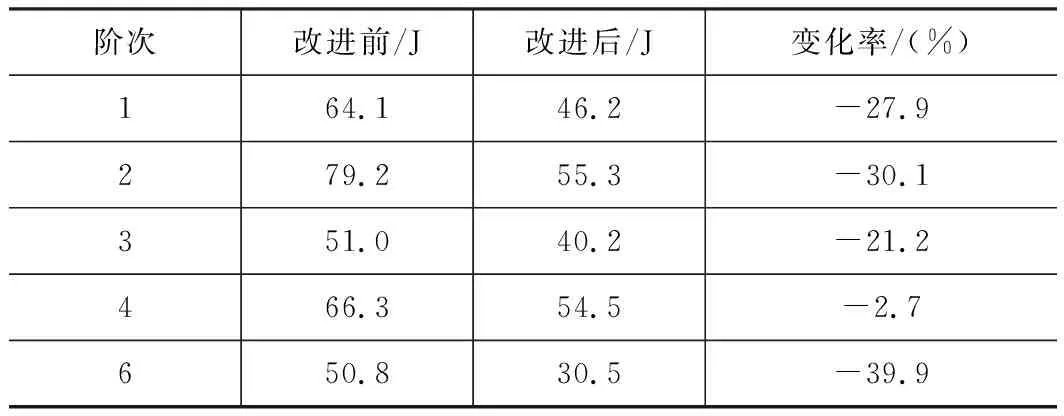
表2 龙门架改进前后动能标准差

表3 龙门架改进前后势能均方差
进一步比较改进前后的龙门架固有频率,见表4,看出改进后的结构各阶固有频率都有较大的提高,说明改进后的结构动态性能得到了提高。

表4 龙门架改进前后前六阶固有频率
4 结语
本文提出以能量平衡为主、振型分析为辅,通过改善机床部件能量分布的均匀性来提高机床动态性能的方法,通过对数控雕铣机龙门架的动态优化应用实例分析,表明该方法可以快速找到结构的薄弱位置,帮助结构设计人员有针对性的优化机床结构,减少了优化设计中的盲目性。该方法具有很强的实际工程意义。
——《势能》

