考虑能耗的制造车间单AGV路径规划研究*

张中伟 李俊兰 吴立辉 武照云

(河南工业大学机电工程学院，河南 郑州 450001)

节能减排现已成为全球制造业实现可持续发展的共识[1]。机床作为机械加工工艺过程的执行主体，长期以来是节能机械加工系统研究的焦点，物料运输系统作为机械加工系统的重要组成部分，其相关设备能耗却较少被关注[2]。自动导引运输车(automated guided vehicle，AGV)作为典型的物料运输设备，目前在制造车间逐渐得到广泛应用。相应地，AGV路径规划(AGV path planning，AGVPP)是需要重点关注的一个问题。

关于制造车间AGVPP，目前研究大都关注运输距离、时间和成本等目标[3-5]，而能耗或能耗相关的环境影响指标却很少涉及。AGV普遍采用电池作为动力来源，在行驶过程中会持续消耗电能。当电池电量不足需要充电或更换电池时，AGV将暂时失去运输能力，从而影响AGV系统对运输任务的指派分配和调度，对车间物料运输系统运行造成干扰扰动。

针对现有研究存在的问题和不足，本文在制造车间环境下，通过合理假设与分析，建立了以运输距离和能耗为优化目标的节能单AGV路径规划(energy-efficient single AGVPP，ESAGVPP)模型。进而，利用粒子群优化算法(particle swarm optimization，PSO)求解模型。最后，通过案例研究验证了模型节能效果和求解方法的有效性。

1 问题描述与建模

1.1 模型假设

AGVPP通常包含两个步骤：(1)AGV应用环境的表达；(2)结合优化目标进行最优路径搜索[6]。

关于AGV应用环境表达，目前主要有拓扑地图、栅格地图和轨迹图3种形式[7]。其中拓扑地图创建简单，计算效率高，得到了广泛应用，尤其适用于车辆可行驶路径已知情形。鉴于此，本文采用拓扑地图表达制造车间环境，将路径交叉点、停车点、工位装/卸物料点等具有特殊意义的位置抽象为节点，连接节点之间的路径用带权重的边表示。此外，提出以下建模假设：

(1)研究针对单载AGV。

(2)车间AGV行驶道路为单行双向。

(3)不考虑货物体积和AGV装/卸货时间。

(4)零时刻分配运输任务时，AGV可用，且一旦开始执行运输任务就不能中断。

(5)与车间预设道路相对应，AGV只存在直行和转弯两种运动轨迹，加速和减速运动只发生在直线路段，且加速度分别保持不变，其余情况下AGV匀速行驶。

(6)AGV行驶时车轮不打滑。

1.2 模型表示

以AGV总运输距离Dtotal和能耗Etotal，为优化目标的ESAGVPP模型定义在用无向图G=(V,A)表示的车间拓扑地图上，其中V={1, 2，…,n}是节点集合，A={(i,j):i,j∈V,i≠j}是边集合，且边(i,j)的权重用连接节点i和j的路段距离dij表示。AGV运输路径用从运输任务起始节点出发，可至目标节点的遍历过的有序节点组成的集合S表示。其他建模所需参数和决策变量如表1所示。

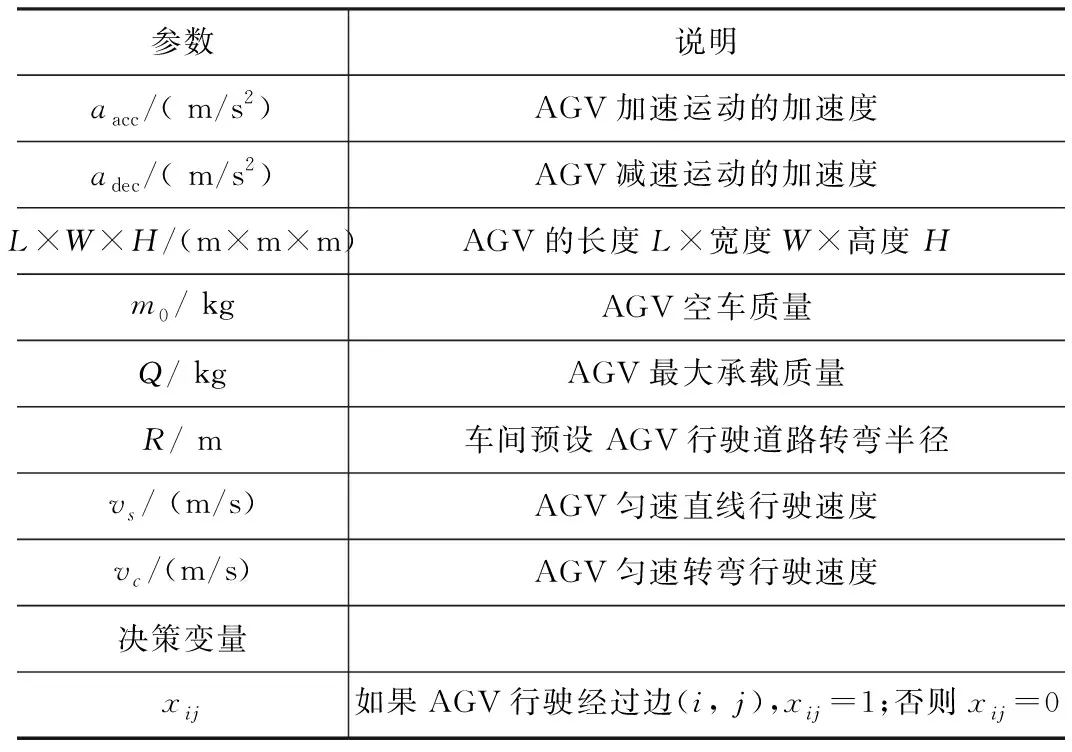
表1 模型参数和决策变量定义表

Dtotal包括运输遍历节点间的距离D和节点区域行驶距离Dnode，其中D可表示为：

(1)

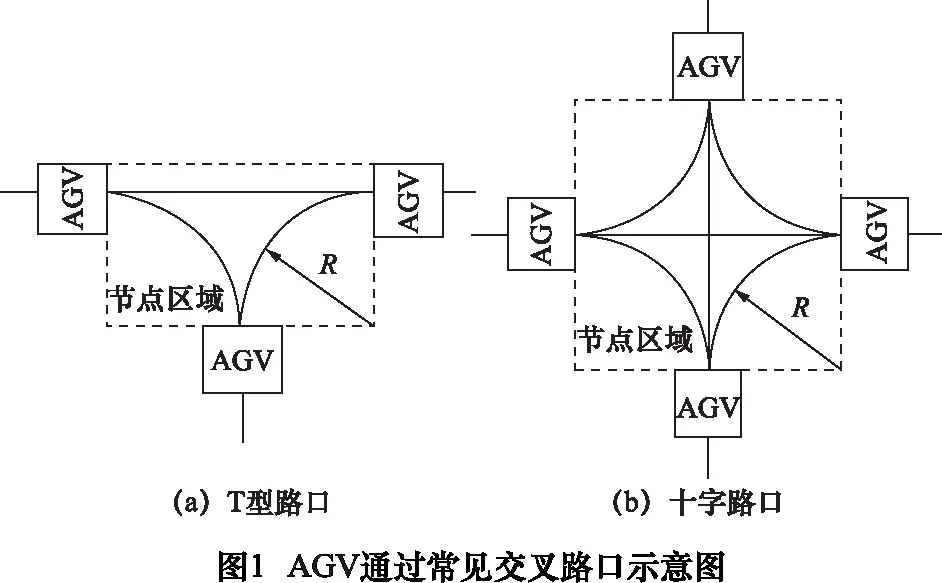
Dnode主要取决于AGV通过节点的形式。制造车间常见的T形路口和十字路口如图1所示，当AGV直行和转弯通过它们时，行驶距离分别为2R和πR/2。对于任一可达运输路径S，决策变量xij的值可随之确定，进而确定AGV直行通过的节点数目(nL)和转弯通过的节点数目(nT)。相应地，Dnode可以表示为：

(2)

进而能够计算得出Dtotal：

Dtotal=D+Dnode

(3)

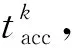
(4)

(5)

式中：v0k和vtk分别表示AGV在第k个加速运动阶段的初始速度和终点速度，m/s；v0l和vtl分别表示AGV在第l个减速运动阶段的初始速度和终点速度，m/s。进而，AGV加速运动总位移Dacc和减速运动总位移Ddec可分别表示为：

(6)

(7)

相应地，可分别得出AGV匀速直线行驶的总距离Dulm和匀速转弯行驶的总距离Dutm：

Dulm=D-Dacc-Ddec+2RnL

(8)

(9)

结合式(4)～(9)，可以计算得出Ttotal：

(10)

时间边界确定后，为降低能耗分析难度，从运动角度对AGV能耗进行分解。AGV消耗能量所维持的运动类型包括待机运动、加速运动、减速运动和匀速运动。其中，待机运动是基本运动，贯穿执行于运输全过程，涉及控制器、导航传感器、行走驱动电机驱动器、散热风扇等能量源。由于这些能量源一般功耗相对固定，故待机运动功率Pso，可认为是它们的额定功率之和。其余3种运动涉及的能量源主要是行走驱动电机。

AGV行驶中通常需克服摩擦阻力、空气阻力、坡度阻力和加速阻力4种阻力[8]。然而，车间地面一般较平坦，且AGV移动速度较慢，故本文忽略空气阻力和坡度阻力。另外，AGV减速时，行走驱动电机输出功率一般急剧降低，甚至为0，为此本文忽略维持减速运动的能耗，但减速运动时间会影响基本运动能耗，能耗分析时仍需考虑。

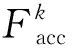
(11)

式中：Cr为滚动摩擦系数；Mk为第k个加速运动阶段车辆和货物的总质量，kg；g为重力加速度常量，取9.81 m/s2。进而，AGV由于加速运动而消耗的总能量Eam为：

(12)

式中：η表示行走驱动电机功率因数。

(13)

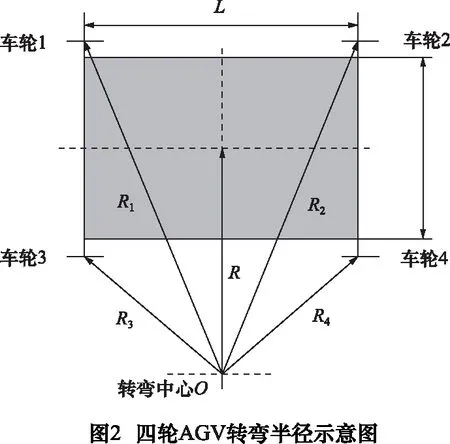
式中：My表示第y个匀速运动阶段AGV和货物的总质量，kg。受车体结构约束，AGV转弯时内外侧车轮的转弯半径存在差异。常见的四轮AGV转弯半径示意图如图2所示，由此可得出：

(14)

(15)

进而计算得出AGV匀速运动在转弯路段的总能耗Eutm：

(16)

AGV匀速运动在直线路段的总能耗Eulm则可表示为：

(17)

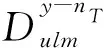
Etotal=PsoTtotal+Eam+Eutm+Eulm

(18)

ESAGVPP模型的优化目标为：

(19)

约束为：

m0≤Mk,My≤m0+Q,∀k,y

(20)

(21)

(22)

(23)

xij∈{0,1},∀i,j∈V,i≠j

(24)

约束条件式(20)表示AGV有效运输载荷不能超过其载重极限；式(21)表示可达运输路径中每个节点只能被访问一次；式(22)表示离开可达运输路径中的每个节点只能通过一条边；式(23)规定任意可达运输路径中不允许出现后退路径和环路；式(24)表示xij是二进制决策变量。

2 基于PSO求解模型

AGVPP本质上也是一个多目标优化问题，以进化算法、群智能算法为代表的现代智能算法凭借搜索效率高、自适应性强、自学习等优点，非常适合在给定时间内获得多目标优化问题的精确或近似Pareto解集[9]，故本文利用PSO算法求解模型。

粒子编码方案设计关系求解问题的本质特征和算法效率，本文采用基于优先级的间接编码方案[10]表达AGV运输路径。结合前述参数定义，种群粒子z可表示为(Xz1,Xz2，…，Xzn，Vz1，Vz2，…，Vzn)的形式。前n个元素记录粒子位置信息，分别对应车间拓扑地图的n个节点，取值为属于[0, 1]的随机数；后n个元素分别表示粒子在搜索空间各维的速度，取值范围为[-1, 1]。根据粒子编码信息提取AGV运输路径的具体流程如图3所示。

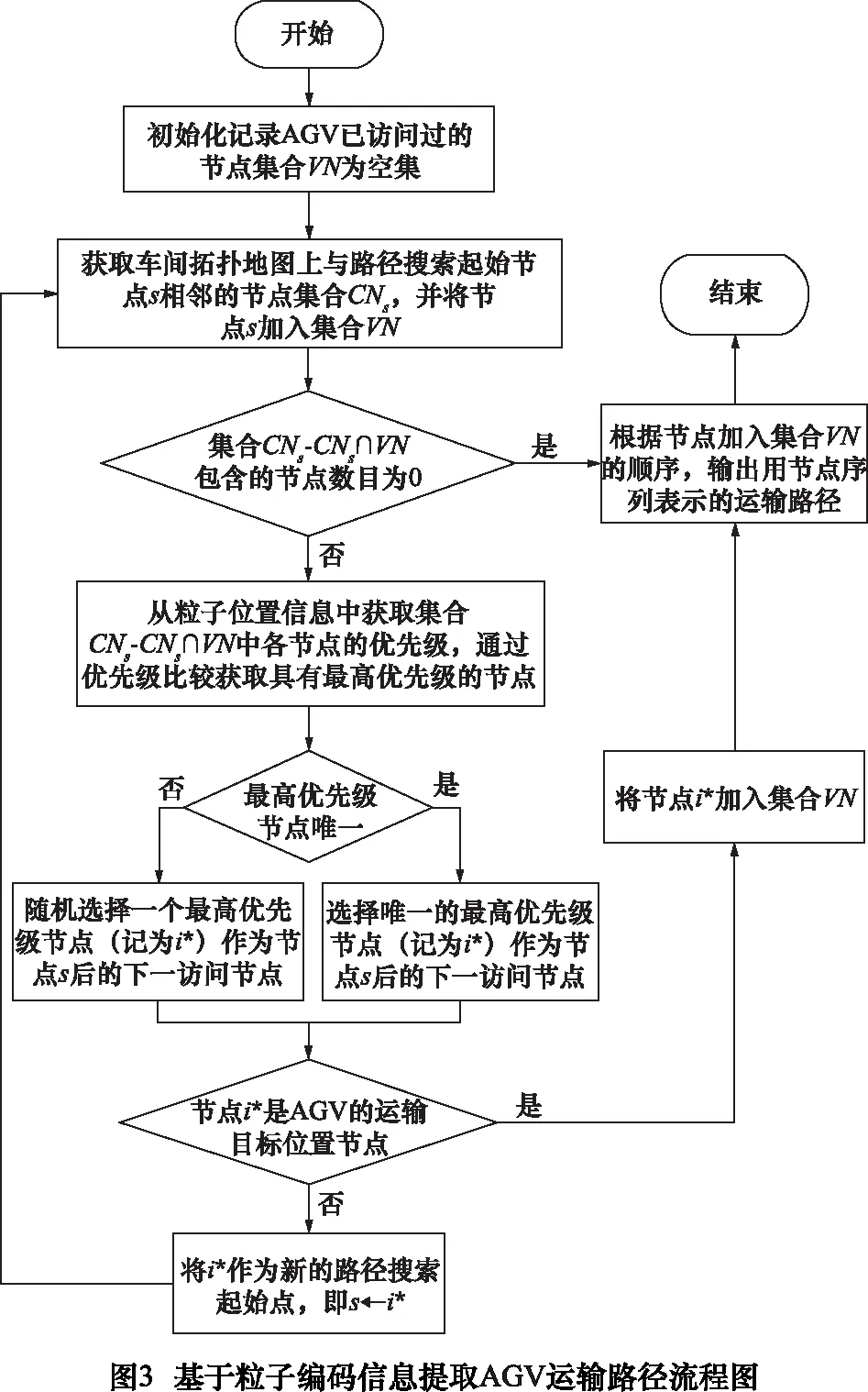
尽管按照图3所示流程提取AGV运输路径能够有效避免产生后退路径和环路，但仍可能产生未结束于预设目标节点的无效路径。对于任一粒子，如果提取的AGV运输路径有效，则根据式(3)和(18)计算优化目标值；如果无效，则对粒子施加惩罚，分别赋予Dtotal和Etotal一个极大值。进而，针对粒子群个体适应度评价，本文基于Pareto支配关系对不同粒子进行比较。

PSO算法的关键参数(如种群规模，惯性权重，认知加速度系数、社会加速度系数等)设置规则和关键算法过程(如拥挤度排序，粒子速度更新、位置更新等)可参考文献[11]，本文不再赘述。

3 案例研究

首先在某航空制造企业的一个航空精密零件制造车间进行实验，该车间已广泛应用AGV进行物料搬运。出于保护企业隐私，产品、设备型号和供应商，关键技术参数等信息进行了隐藏或不影响案例研究效果的处理。建立的车间拓扑地图如图4所示，车间交叉路口的转弯路段半径R均为0.85 m。

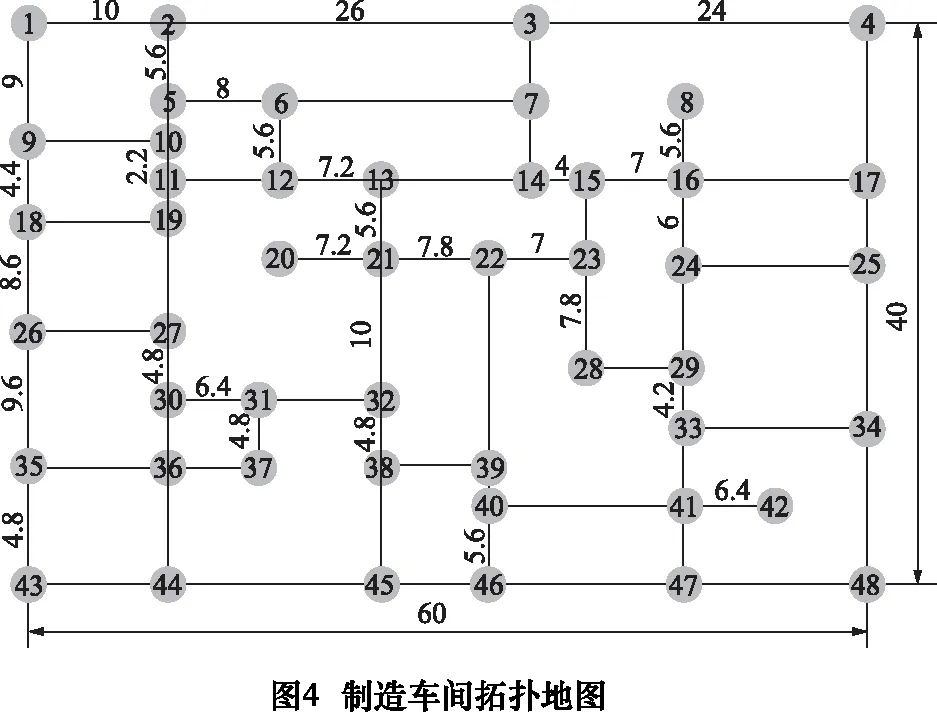
实验选用的单载AGV利用4个额定功率为80 W的伺服电机分别驱动4个车轮，其主要技术参数如表2所示。PSO算法在Intel core(TM)i5-6500 3.20GHz CPU，16GB RAM，Windows 7的PC上用Matlab语言实现，关键参数设置如表3所示。

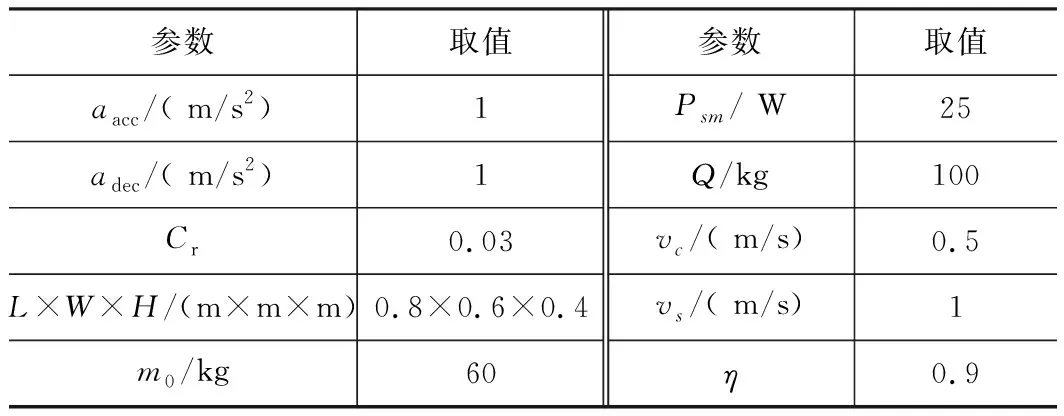
表2 AGV主要技术参数

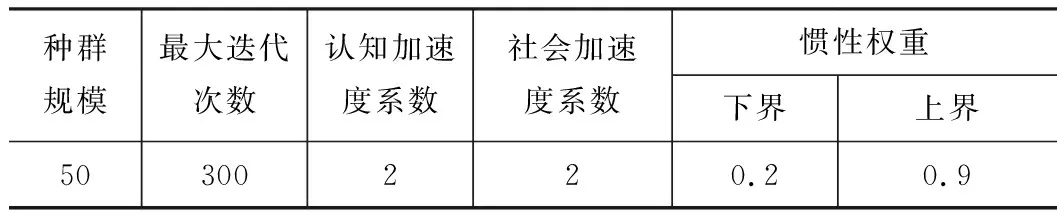
表3 PSO算法参数设置

车间目前进行AGVPP主要考虑尽量减少车辆行驶转弯次数。实验初始时，AGV载着质量为30 kg的工件停在节点9，运输目标节点是42。应用ESAGVPP模型，运行PSO算法5次，求解得到惟一的AGV最优行驶路径，其与优化前的AGV路径规划结果对比如表4所示。

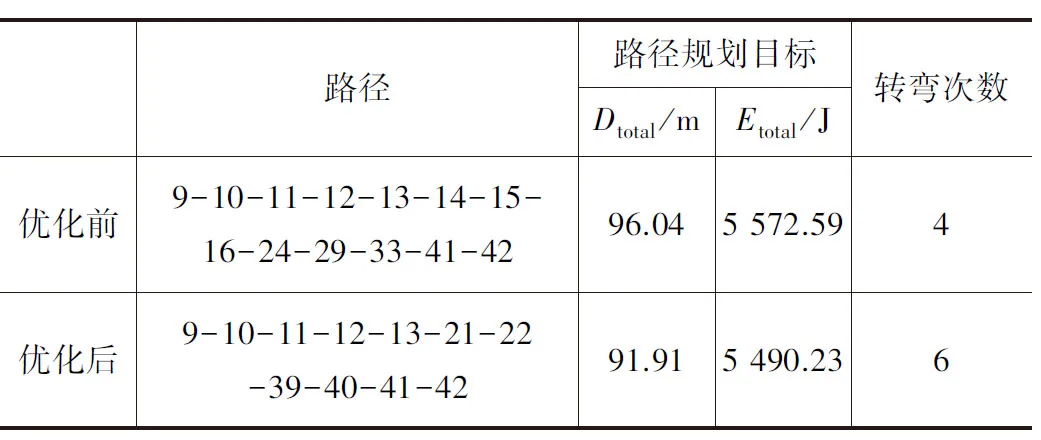
表4 优化前后AGV路径规划结果对比

由表4可知，Dtotal和Etotal都得到了优化，其中Dtotal缩短了4.3%，Etotal降低了1.5%，且并未呈现转弯次数增加，AGV行驶过程中加减速次数也增加，从而造成能耗增加的现象。因此，考虑能耗的AGVPP是提高AGV使用能效的一种可行方法。

另外，为验证本文应用的PSO算法有效性，结合文献[12]的路径规划案例(如图5所示)，并以运输距离为优化目标进行不同算法求解效果对比。

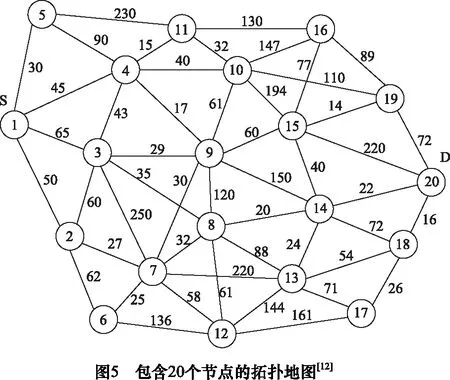
仍采用表3所示的算法参数，运行PSO算法5次，搜索得到从节点1到20的最短路径为“1-3-8-14-20”，对应路径长度为142。这与文献[12]利用遗传算法搜索得到的最优路径结果相同。不失一般性，假设初始节点是5，目标节点是17时，运行PSO算法5次，得到的最短路径为“5-1-3-8-14-20-18-17”，对应路径长度为214，这与使用Dijkstra算法得到的结果相同。因此，本文使用的PSO算法，尤其设计的粒子编码方案和路径提取方法是有效的。

4 结语

针对制造车间的节能生产需求，建立了以运输距离和能耗为优化目标的ESAGVPP模型，并利用PSO算法对其求解，设计了反映问题解特征的粒子编码方案。所建立的ESAGVPP模型实际上也反映了通过为AGV合理选择运输路径来提升AGV使用能效的方法。案例研究验证了所提模型和求解方法的有效性。后续将针对多载AGV以及多个AGV进行节能路径规划研究，并改进求解算法。