基于黏弹性人工边界条件的岩质边坡动力反应分析

景鹏旭，尹 超，门丽君，许杰夫，杨清逸

(1.中国地震应急搜救中心， 北京 100049； 2.北京交通大学， 北京 100055；3.山西工程技术学院， 山西 阳泉 045000； 4.北京清控人居光电研究院有限公司， 北京 100089)

近场波动有限元计算中建立有限元模型时，需从无限介质中截取出有限计算区域的过程涉及到将无限域模型有限化处理引起的人工边界上的地震动输入问题[1]。人工边界主要分为两类：位移型人工边界条件(透射边界[1]、旁轴近似人工边界[2]等)和应力型人工边界(黏性边界[3]、黏弹性边界[4-6]等)。本文处理无限地基介质对近场区域的影响采用杜修力等[6]提出的黏弹性人工边界。

1 黏弹性人工边界

黏弹性人工边界是指由线性弹簧与黏滞阻尼器并联形成弹簧-阻尼物理元件[4-6]组成的人工边界。

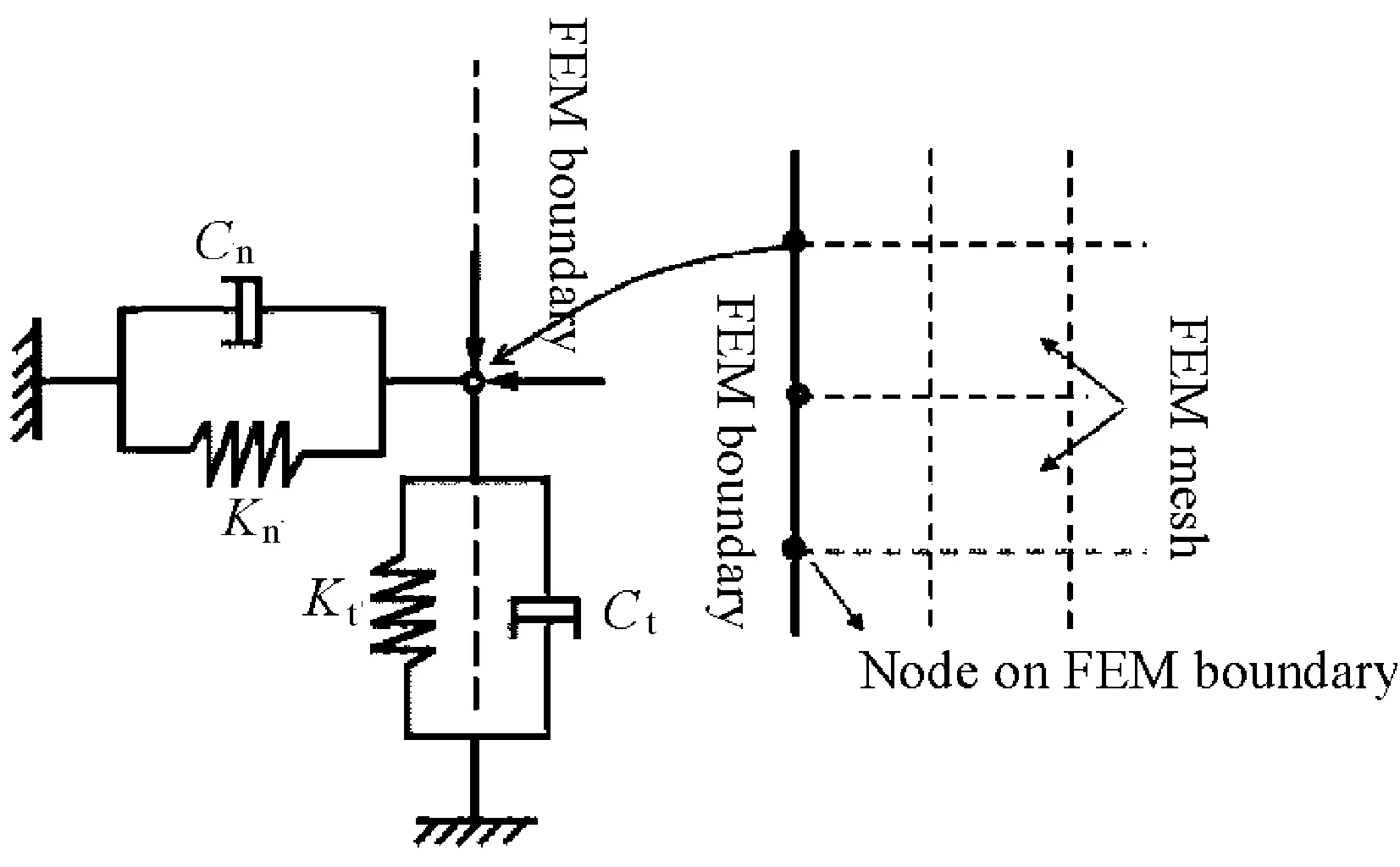
图1 黏弹性人工边界示意图

黏弹性人工边界弹簧、阻尼参数系数分别为：

法向边界：

(1)

切向边界：

(2)

式中：Kn为法向弹簧刚度系数；Kt为切向弹簧刚度系数；Cn为法向阻尼系数；Ct为切向阻尼系数；R为散射波源至人工边界的距离；G为剪切模量；ρ为质量密度；αn为法向黏弹性人工边界修正系数；αt为切向黏弹性人工边界修正系数；A为边界节点所代表的面积；cP为P波波速；cS为S波波速。

2 人工边界的地震动输入方法的验证

计算平面半空间垂直入射时，P波和SV波的等效节点力。图2为P波或SV波垂直入射于待研究区域的模型。

由图2的示意图，当地震波垂直入射于有限研究区域时，自由表面处不会发生波型转换，并且在自由表面处遵循位移为入射波场二倍这一定律。以P波为例计算垂直入射时的等效地震荷载[7-9]。

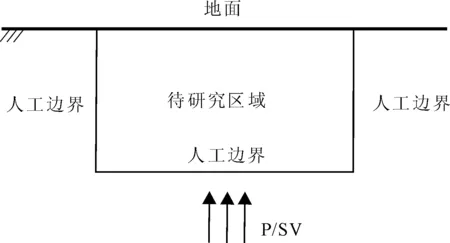
图2 P波或SV波垂直入射模型

P波垂直入射下等效地震荷载的计算公式如下：

底边界：

(3)

(4)

侧边界：

(5)

(6)

式中，

Δt1=2H/cP；Δt2=y/cP；Δt3=(2H-y)/cP。

为验证黏弹性人工边界参数和建立的P波二维输入方法，模拟均匀半空间内P波传播过程。建立二维有限元模型，截取800 m×400 m的矩形有限区域进行研究，入射波选用一宽0.25 s，持时2 s的狄拉克脉冲，其位移时程曲线见图3。输入的集中荷载为单一脉冲荷载，p(t)=p0·f(t)，其中P0=50 kN,T0=0.25 s。其表达式为：

(7)

式中，G(x)=(x)3H(x)，其中H(t)为Heaviside阶梯函数。

介质的材料参数如下：密度ρ为2 000 kg/m3，弹性模量E为1.25 GPa，泊松比υ为0.25，相应的P波波速和SV波波速分别为cP=866 m/s，cS=500 m/s。选取模型底部中点A和顶部中点B为监测点，见图4。

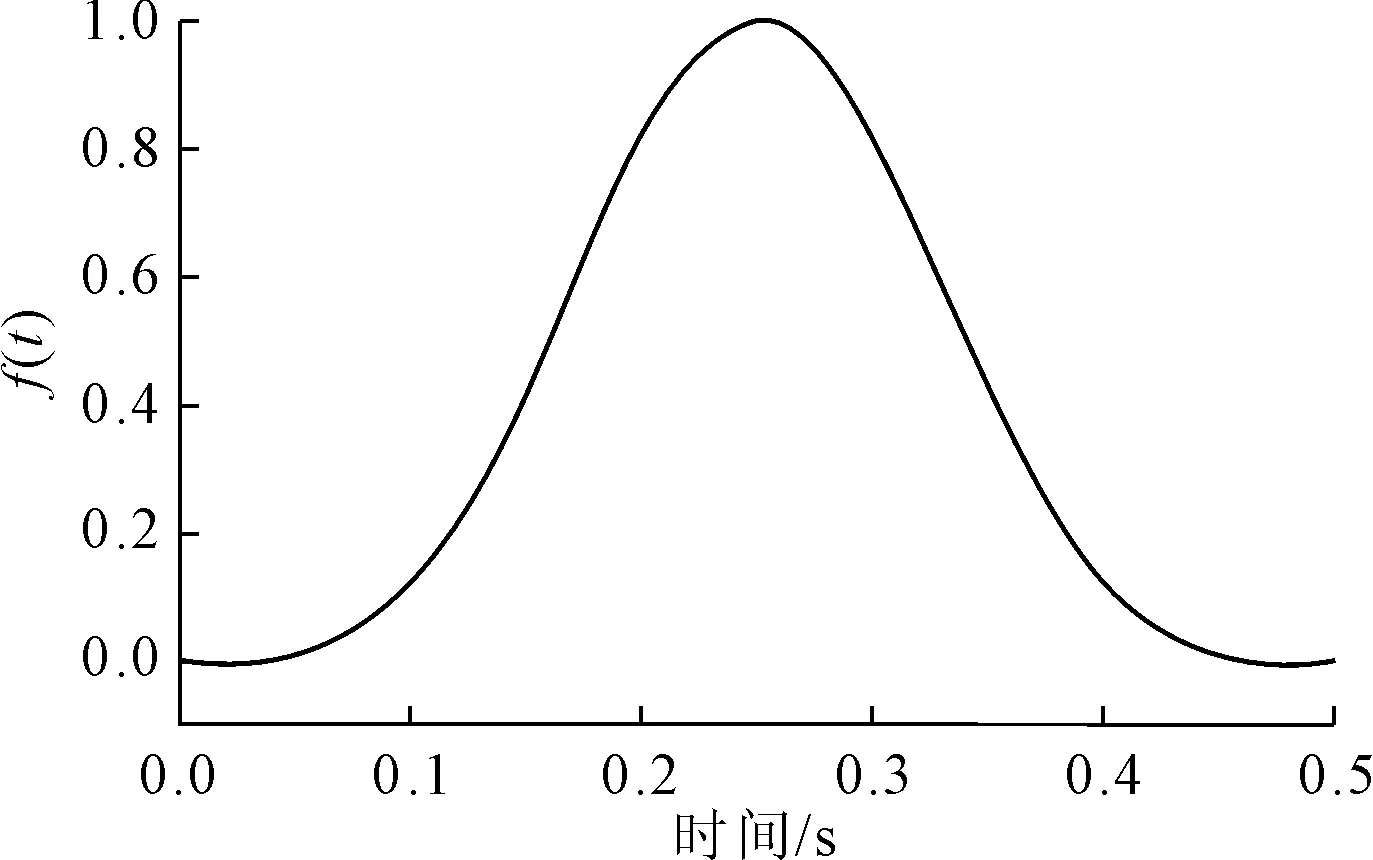
图3 脉冲函数f(t)时程曲线

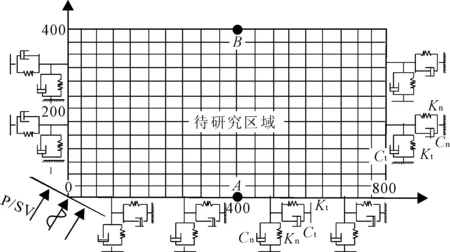
图4 添加黏弹性人工边界的有限元模型

图5给出了监测点A点和B点的竖直方向位移Uy时程曲线。从图5可以看出，数值解与理论解基本吻合，表明P波垂直入射输入方法的正确性。SV波与P波的结果类似，地表面的位移也是底面的二倍。只不过对于入射P波，我们监测的是竖直方向位移，若入射SV波，监测的是水平方向位移。这里仅以P波为例，证明对于地震波的输入是准确的。

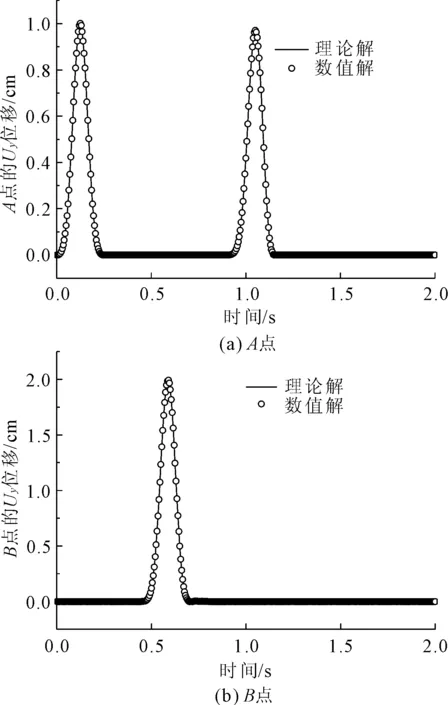
图5 P波垂直入射监测点A点和B点的Uy位移时程曲线

3 边坡尺寸形状对地震响应的影响

根据上述分析，本文已经实现了地震波在数值模型中的添加，并且对其有效性和精度进行了相应的验证，从而为后续将要分析的边坡放大效应奠定了基础[10-11]。

基于上述波动输入方法，接下来对边坡的放大效应展开分析。首先建立边坡分析模型，见图6。地震波假设为P波入射，模型底部和两侧布设黏弹性人工边界，分析边坡在不同尺寸(坡高，坡角)以及不同地震波作用下，坡顶附近的放大效应变化[12]。

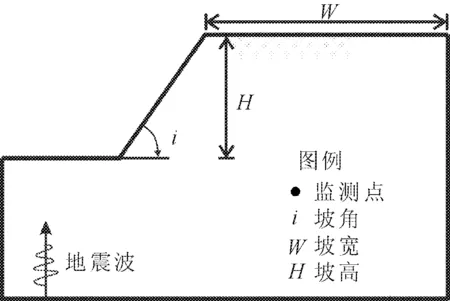
图6 岩质边坡分析模型

为分析卓越频率对场地地震响应的影响，本文采用正弦脉冲作为输入场地的P波。分别施加持时为0.25 s、0.50 s和1.00 s的正弦脉冲(对应的卓越频率分别为3.50 Hz、1.56 Hz和0.78 Hz)。三种正弦脉冲的加速度时程见图7。

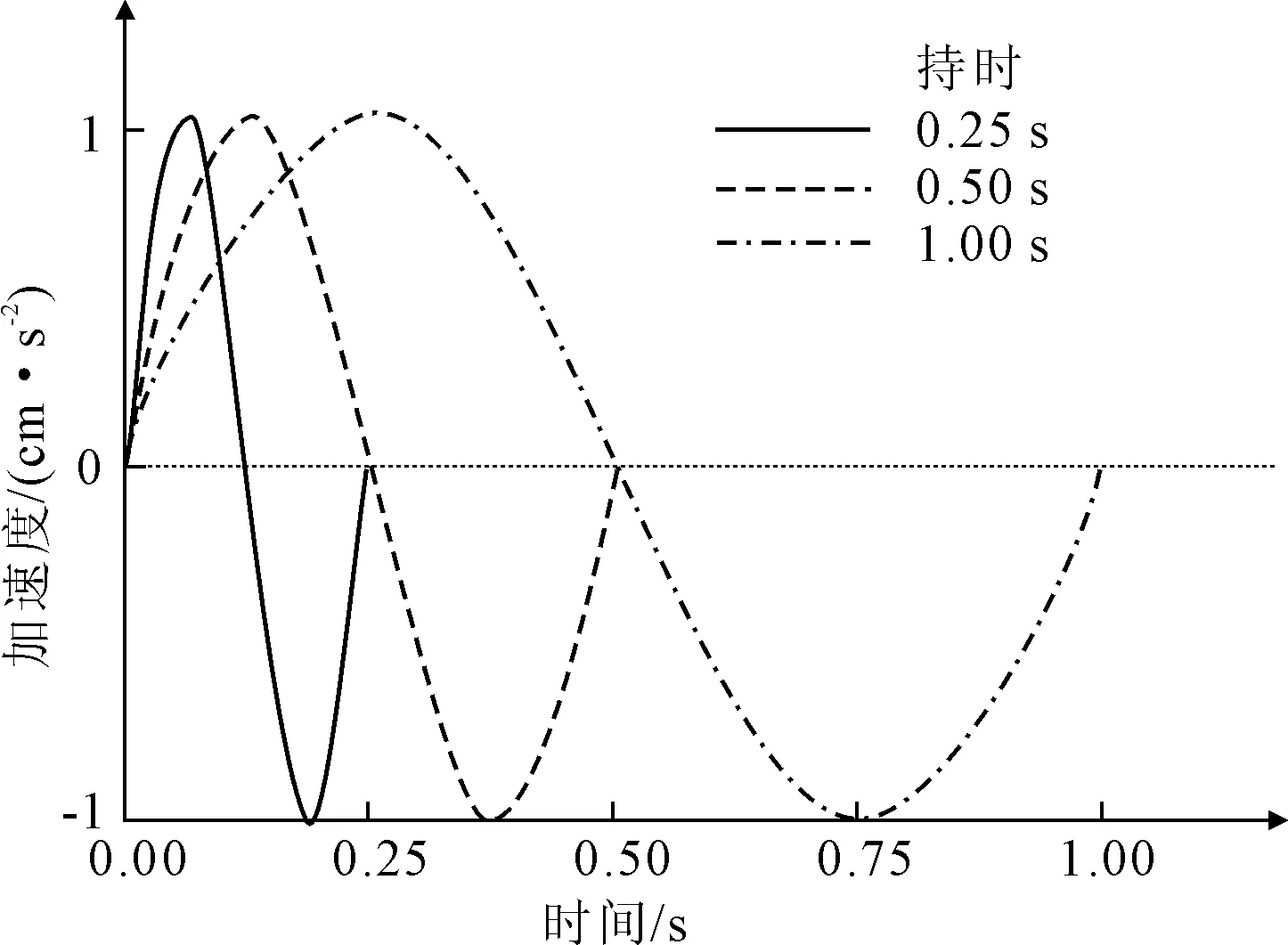
图7 正弦脉冲加速度时程

定义地震动PGA放大系数(简称放大系数)β为观测点地表地震动峰值A0与输入地震动峰值A1的比值，即β=A0/A1。采用β来描述边坡对波动的放大效应。监测地表面和边坡表面的放大系数，重点监测两侧坡脚和坡顶的放大系数。按照坡高将边坡地表面地震响应放大系数列于图8—图10中。为了方便下文论述，0.25 s持时的正弦脉冲称为高频脉冲，0.50 s持时正弦脉冲称为中频脉冲，1.00 s持时正弦脉冲称为低频脉冲。高宽比1.0∶2.0的凸起地形称为缓坡，高宽比1.0∶1.0的凸起地形称为陡坡，高宽比1.0∶0.5的凸起地形称为急陡坡。

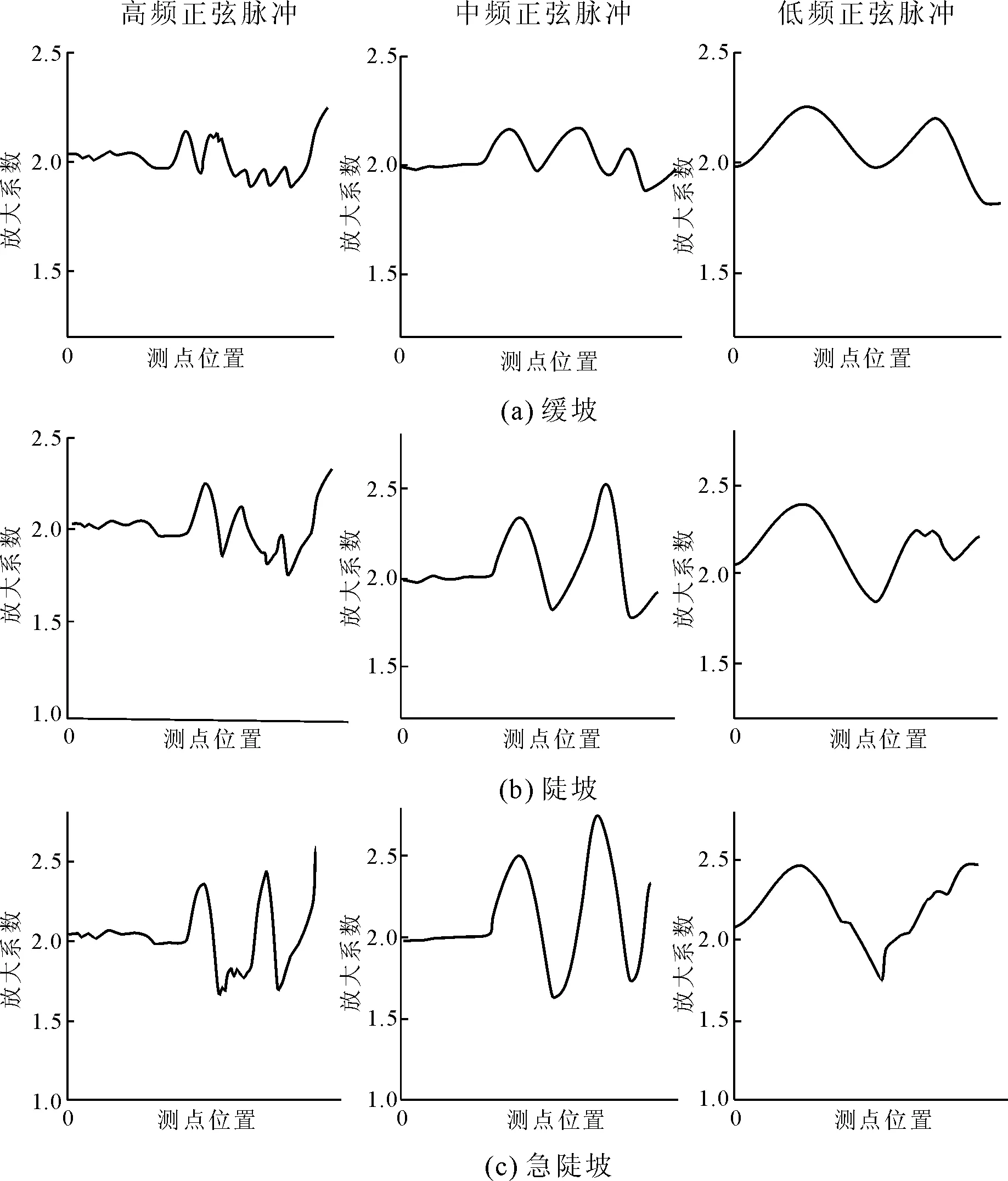
图8 坡高30 m地表放大系数

图8左侧列为入射高频正弦脉冲时边坡坡面的放大系数变化规律：随着边坡的角度变陡，坡面的放大系数也逐渐增加，而更为显著的则是坡面放大系数变化范围的增加。同理，图8中间列为入射中频正弦脉冲的放大系数，对于入射中频正弦脉冲来说，随着边坡坡角变陡，坡面放大系数的变化范围也是逐渐变大，且放大系数的值也在逐渐增加。图8右侧列为入射低频正弦脉冲的放大系数，对于入射低频正弦脉冲来说，放大系数的变化范围和放大系数的数值并没有像前两种脉冲时的那种变化。从缓坡变换到急陡坡，放大系数的变化范围增长率相对较小。横向比较，在相同坡角下，随着入射地震波的频率降低，坡面放大系数变的越来越平缓。这种情况无论是对于缓坡、陡坡还是急陡坡来说，都是一样的。即使是急陡坡，其在低频下对坡面的地震响应也不如在高频时的丰富。这是因为低频会过滤一部分成分，导致边坡坡体形态对地震波的响应不敏感。因此在分析边坡的放大效应问题时，地震波频率是一项非常重要的指标。其与边坡尺寸共同构成了边坡地震响应的特点。

与分析坡高30 m的情况相同，图9左侧列为入射高频正弦脉冲时边坡坡面的放大系数变化规律：随着边坡的角度变陡，坡面的放大系数也逐渐增加，而更为显著的则是坡面放大系数变化范围的增加。同理，图9中间列为入射中频正弦脉冲的放大系数，对于入射中频正弦脉冲来说，随着边坡坡角变陡，坡面放大系数的变化范围也是逐渐变大，且放大系数的值也在逐渐增加。图9右侧列为入射低频正弦脉冲的放大系数，对于入射低频正弦脉冲来说，放大系数的变化范围和放大系数的数值并没有像前两种脉冲时的那种变化。从缓坡变换到急陡坡，放大系数的变化范围增长率相对较小。若我们比较不同地震波频率对地形放大效应的影响。在相同坡角下，随着入射地震波的频率降低，坡面放大系数趋于平缓。与此相同，这种情况对于缓坡、陡坡和急陡坡是一样的：在低频下对坡面的地震响应不如在高频时的丰富。因为低频地震波的波长相对较长，会跨过边坡，从而导致一些应有表现出的成分会被过滤掉，从而引起边坡坡体形态对地震波的响应不敏感。因此在分析边坡的放大效应问题时，地震波频率是一项非常重要的指标，其与边坡尺寸共同构成了边坡地震响应的特点。

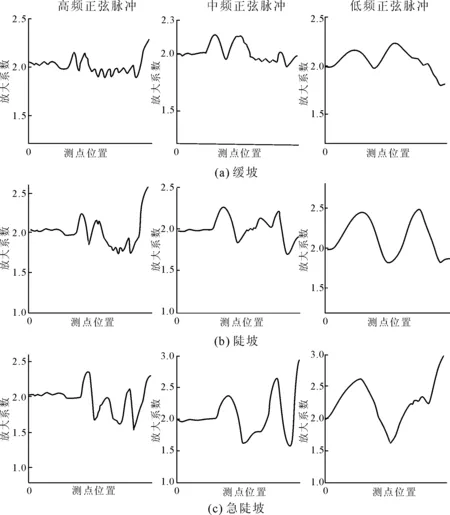
图9 坡高50 m地表放大系数

与分析坡高30 m和坡高50 m的情况相同，图10左侧列为入射高频正弦脉冲时边坡坡面的放大系数变化规律：随着边坡的角度变陡，坡面的放大系数也逐渐增加，而更为显著的则是坡面放大系数变化范围的增加。同理，图10中间列为入射中频正弦脉冲的放大系数，对于入射中频正弦脉冲来说，随着边坡坡角变陡，坡面放大系数的变化范围也是逐渐变大，且放大系数的值也在逐渐增加。图10右侧列为入射低频正弦脉冲的放大系数，对于入射低频正弦脉冲来说，放大系数的变化范围和放大系数的数值并没有像前两种脉冲时的那种变化。从缓坡变换到急陡坡，放大系数的变化范围增长率相对较小。若我们比较不同地震波频率对地形放大效应的影响。在相同坡角下，随着入射地震波的频率降低，坡面放大系数趋于平缓。同样的，这种情况对于缓坡、陡坡和急陡坡是一样的：在低频下对坡面的地震响应不如在高频时的丰富。因为低频地震波的波长相对较长，会跨过边坡，从而导致一些应有表现出的成分会被过滤掉，从而引起边坡坡体形态对地震波的响应不敏感。因此在分析边坡的放大效应问题时，地震波频率是一项非常重要的指标。

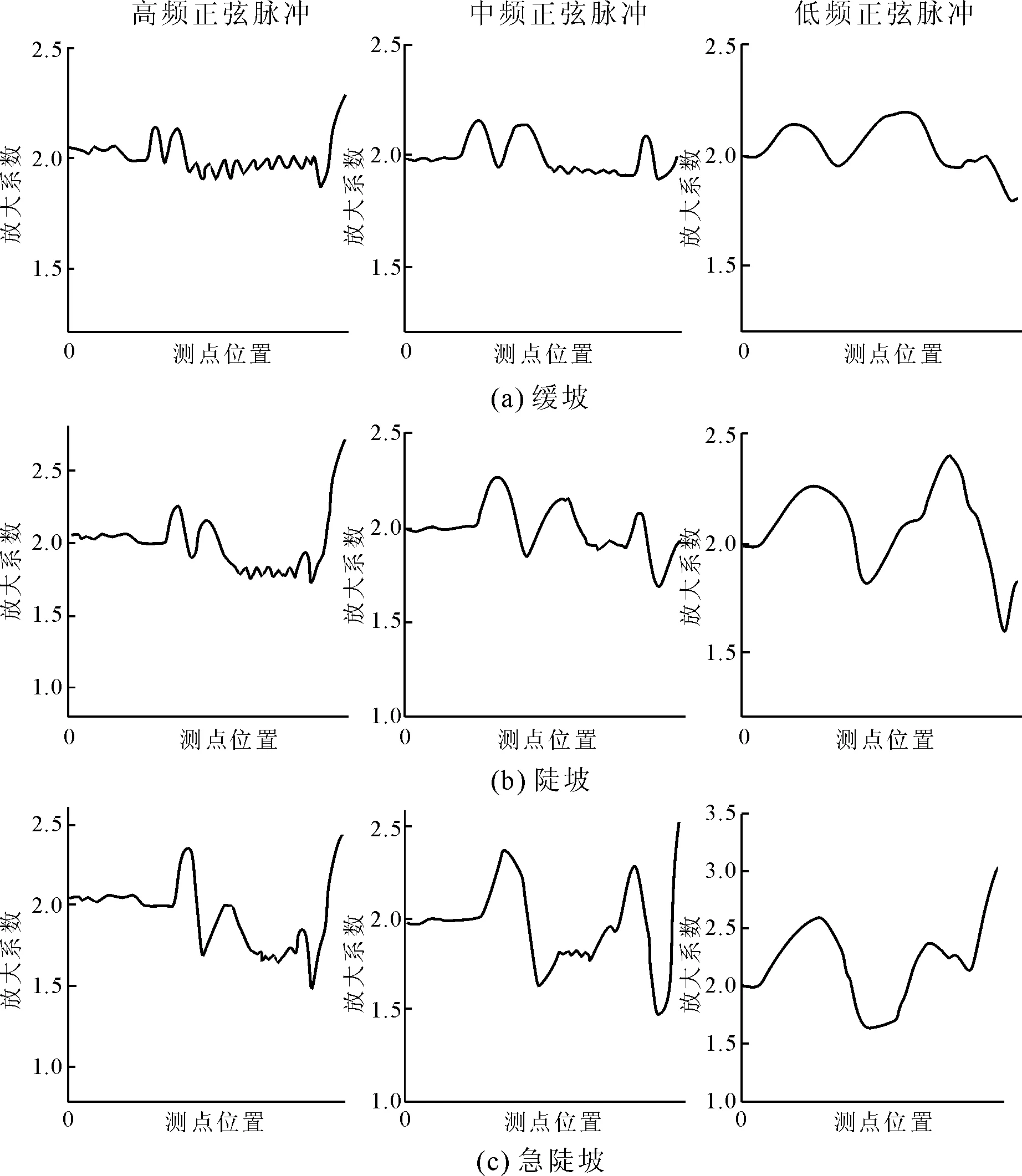
图10 坡高70 m地表放大系数

对于图8—图10来说，我们是以不同坡高作为标准考虑的坡角和地震波频率对放大效应的影响，接下来我们需要分析在相同坡角和地震波频率作用下，不同坡角对地形放大效应的影响。我们只需要将图8、图9和图10对应的位置进行对比即可得到。对比可以看到，不同坡高对于地震放大效应的影响较小。例如比较坡高30 m、50 m和70 m处，高宽比都为1.0∶2.0时，高频地震波入射时的放大系数。可以看到对于坡脚处和坡顶处的突变点，在不同坡高下结果是相同的。差别仅在于边坡越高，坡脚距离坡顶的距离越长，这部分的动力响应越明显。

4 结论及建议

对于边坡的地震响应来说，地震波频率和边坡坡角是地震响应的决定性因素，坡高对于边坡特征点(坡脚、坡顶)的变化敏感性较低。结论如下：

(1) 对于同一地震波频率，不同坡高对于地震放大效应的影响较小，差别仅在于边坡越高，坡脚距离坡顶的距离越长，这部分的动力响应越明显。

(2) 对于同一边坡角度，随着入射地震波的频率越高，坡面的放大系数逐渐增加。

(3) 对于同一边坡高度，随着边坡的角度变陡，坡面的放大系数逐渐增加。

因此在分析岩质边坡的动力放大效应时，我们应重点关注坡角的影响。