基于层合板理论的多层加筋碎石垫层承载特性分析
霍知亮,郎瑞卿,闫澍旺,崔玉萍,高安荣,黄永杰
(1.天津大学 建筑工程学院, 天津 300072; 2.天津市市政工程设计研究院, 天津 300051; 3.天津市软土特性与工程环境重点实验室, 天津 300384;4.中交基础设施养护集团有限公司, 北京 100020)
在传递荷载的过程中,加筋垫层受到竖向荷载作用产生弯曲变形,此时由于土工格栅与碎石之间较强的相互嵌锁固定作用使其具有一定的整体性,能够承担一定的横向外力,即具有部分程度上建筑结构中梁抗弯、抗剪的能力。在预制刚性桩-网复合地基中,加筋垫层自身极限承载能力的计算对于整个工程的安全性十分重要[1]。
近年来已有学者从室内试验、现场试验、数值模拟等多个方面对加筋垫层极限承载能力进行了分析:Yang[2]、Gray等[3]、Shewbridge等[4]、李广信等[5]及Lang等[6]通过三轴试验和直剪等试验揭示了加筋材料对碎石抗剪强度的增强机理,并提出了抗剪强度计算方法,但以上研究多集中于小比尺试验,无法反映多层加紧垫层宏观承载特性。杨明辉等[7]、Shields等[8]、邓岳宝[9]和李磊[10]分别提出了测量加筋碎石垫层刚度的试验方法,揭示了由散体材料和抗拉材料合成材料的抗弯特性,并提出了加筋碎石垫层刚度取值范围。Ariyarathne等[11]、Khabbazian等[12]、Zhao等[13]、张海太等[14]及陈昆明等[15]结合数值模拟方法,通过将碎石加筋垫层假定为不同材料,研究了加筋垫层的荷载传递特性和承载特性,但模拟中多将多层加筋垫层视为弹性体,忽略了加筋垫层自身强度的影响。以上成果对于更清楚的理解加筋碎石垫层的荷载传递特性和承载特性具有较好的借鉴意义。
上述成果对于碎石加筋垫层自身极限承载力研究较少,影响了其在工程领域的进一步推广。因此,考虑碎石与格栅之间的相互作用,对多层碎石加筋垫层自身的极限承载特性进行分析具有重要工程和科学意义。本文考虑多层土工格栅的加筋作用,假设加筋垫层为层合板,根据层合板理论并应用静力平衡条件和应变连续条件,分析得出加筋垫层的极限承载能力计算方法。通过室内试验对理论推导公式进行结果验证,并研究了不同条件因素对承载能力的影响。
1 理论推导
1.1 基本假定
参考无腹筋梁的破坏模式,将加筋垫层视为整体,利用极限状态下静力平衡条件确定其承担外荷载能力。假定共铺设n层格栅,其中第1层距垫层上表面距离为hs,第n层格栅距垫层下表面距离为hx,格栅铺设间隔为△h。计算模型及破坏模式如图1所示。
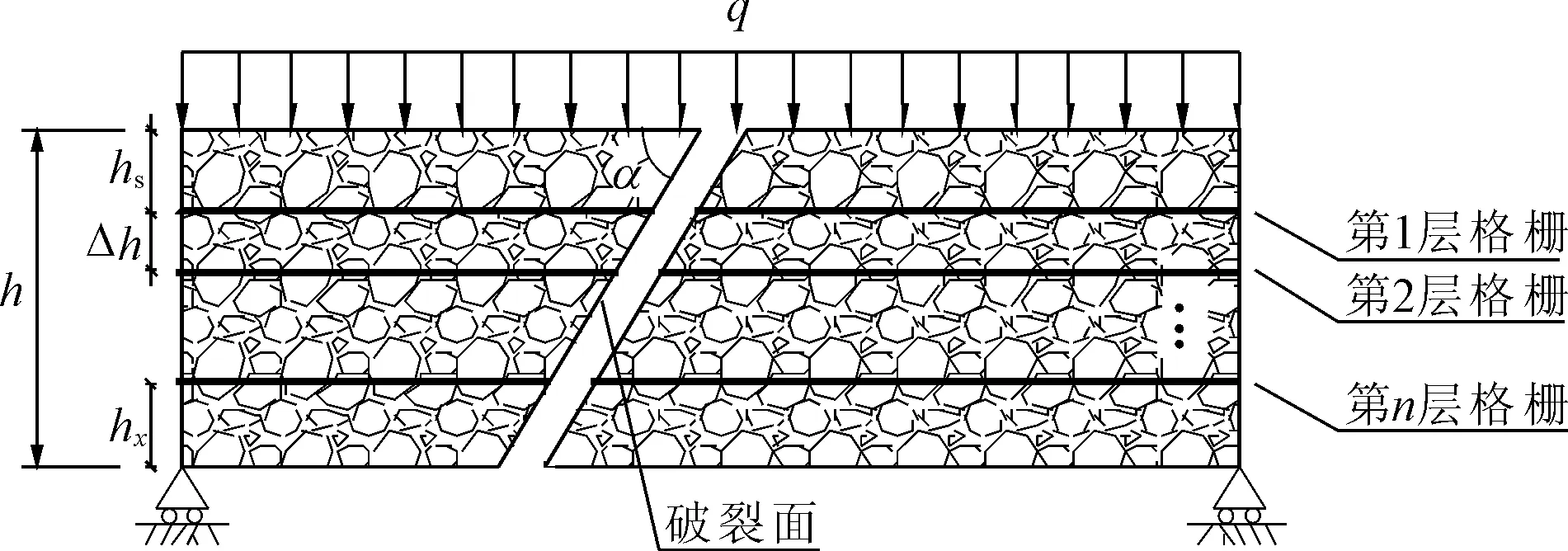
图1 多层加筋垫层力学模型示意图
将破裂面左侧加筋体进行分离受力分析,如图2所示。图中,竖向均布荷载为py,Ay为上表面面积;px为水平向梯形荷载,Ax为侧表面积;隔离体重力为G,支座反力为F,破坏面上第i层筋材的拉力为Ti,隔离体受到右下侧支撑力为σR,剪切力为τ。
主要假定为:(1) 多层加筋垫层中每层土工格栅与碎石均满足应变连续条件;(2) 极限状态时,格栅与碎石摩擦属于塑性摩擦;(3) 整体破坏由破裂面上抗剪强度控制;(4) 参考无腹筋梁的破坏模式,整体剪切破坏时,破裂面与横向力夹角为45°+φ/2。
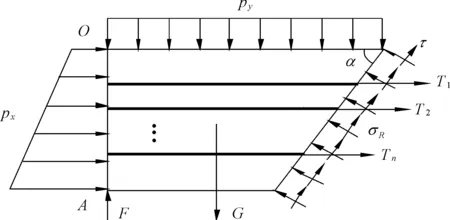
图2 左侧隔离体受力分析图
1.2 承载能力求解
假定破裂面上应变连续,故任意层格栅应变εgi与第n层格栅应变εgn存在如下关系:
(1)
任意层格栅拉力Tgi与第n层格栅拉力Tgn关系如式(2)所示:
(2)
隔离体需满足水平向、竖向静力平衡和合力矩平衡。将图2中左上角点视为原点O,首先计算A点的合力矩。
水平px的值为K0(py+γy),其中K0为碎石垫层静止土压力系数,γ为碎石重度。则px对A点的力矩Mpx为:
(3)
py对A点的力矩Mpy为:
(4)
重力G对A点的力矩MG为:
(5)
式中:D为桩间距;D/2为外荷载作用长度。
剪切力τ对A点的力矩Mτ为:
(6)
各层格栅拉力Ti对A点的力矩MTi为:
(7)
支撑力σR对A点力矩为:
(8)
A点的合距为零,故可得
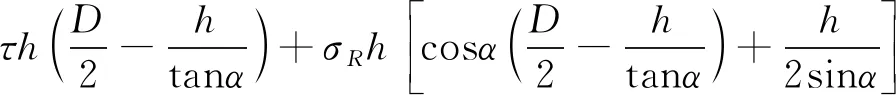
(9)
左侧隔离体受力矢量图如图3所示。

图3 左侧隔离体受力矢量图
根据水平向受力平衡可得:
τhcotα=σRh
(10)
根据竖向受力平衡可得:
(11)
联立式(9)—式(11)并化简可得加筋垫层极限承载力为:
(12)
2 试验验证
某加筋碎石垫层工作特性试验在钢制模型箱中进行[16]。碎石天然重度为20.6 kN/m3,相对密度为2.66,孔隙比为0.50。土工格栅纵向和横向抗拉强度分别为68.4 kN/m和78.2 kN/m,对应伸长率分别为2.7%和2.8%。试验共进行A、B、C三组,其中A组为无加筋垫层时软土承载力试验,B组为软土上布设1层土工格栅加筋碎石垫层,C组为软土上布设2层土工格栅加筋碎石垫层。试验布置图如图4所示。
利用本文方法与实测值对比如表1所示。由结果可知,本文方法计算得到的承载力比实测值稍小,但误差在工程可接受的范围内。

图4 模型试验示意图[16]

表1 理论推导与模型试验结果的比较
3 影响因素分析
由式(12)可知,影响加筋碎石垫层承载能力的因素包括桩间距D,最底层格栅距桩顶位置hx,垫层厚度h,格栅层数n(或格栅间距)和加筋碎石抗剪强度τ。采用单一变量法研究以上因素对承载能力的影响。
3.1 桩间距D
其他因素不变,极限承载力随桩间距D的变化如图5所示。

图5 极限承载能力与桩间距D关系曲线
由图5可知,随着桩间距的增大整体极限承载力降低。由受力分析可知,桩间距越大,则加筋垫层上承担的总荷载越大,则加筋垫层越容易发生破坏。同时,可将桩间距视为梁单元中的跨度,根据简支梁理论可知,跨度越大,则最大弯矩越大,越容易发生破坏。
3.2 最底层格栅距桩顶的距离hx
其他因素不变,极限承载力随hx的变化如图6所示。由图6可知,极限承载力随着hx的增大而减小。hx为最底层格栅距桩顶的距离,该值越大,说明格栅越集中于加筋垫层中间,提供的抵抗力矩越小;反之,则越分散,提供的抵抗力矩越大。
3.3 垫层厚度h
多层加筋垫层厚度h对整体承载能力的影响如图7所示。整体承载能力随着加筋垫层总厚度h的增大而增大。垫层越厚,则更多的材料参与抗弯,斜截面的抗剪强度也越大,故承载能力增大。

图6 极限承载力随hx变化曲线

图7 承载能力随h变化曲线
3.4 格栅层数n
承载能力随格栅层数n的变化如图8所示。增加加筋层数可以明显增强垫层整体承载能力。加筋材料不仅能够提高碎石体的抗剪强度,而且其产生的拉力能够抵抗荷载产生的弯矩,进而增强整体承载能力。

图8 承载能力随n变化曲线
3.5 加筋碎石体抗剪强度τ
整体承载能力随多层加筋碎石体抗剪强度τ的变化如图9所示。从分析结果可知,极限承载能力随着τ的增大而增大。由力学模型分析可知,加筋垫层承载能力由加筋碎石抗剪强度控制,且该力能够提供弯矩以抵消外荷载形成的弯矩。故τ越大,整体承载能力越大。

图9 承载能力随τ变化曲线
4 结 论
本文以土工格栅加筋垫层为研究对象,考虑多层土工格栅的加筋作用,假设加筋垫层为层合板,根据层合板理论并应用静力平衡条件和应变连续条件,分析得出加筋垫层的极限承载能力计算方法,对加筋垫层挠度方程进行求解。通过室内试验对理论推导公式进行结果验证,并研究了不同条件因素对承载能力的影响,得到的结论如下:
(1) 根据加筋垫层的层合板理论,结合静力平衡条件和应变连续条件,推导了其极限承载力计算方法。
(2) 通过室内模型试验的模拟,理论计算与试验结果吻合较好,本文方法可为实际工程提供参考。
(3) 随着格栅层数、垫层厚度、碎石抗剪强度的增加,多层加筋垫层自身极限承载能力增强;随着桩间距和底层格栅距桩帽距离的增大,多层加筋垫层自身极限承载能力降低。

