改进Rowe剪胀方程和南水模型在面板堆石坝中的应用
陈池威,刘国明,赵 辰
(福州大学 土木工程学院, 福建 福州 350108)
随着经典弹塑性、非线性弹性理论广泛应用于水利工程中,面板堆石坝得到迅速发展。选择合理的理论模型有助于预测面板坝的变形,因此研究能够精确反映堆石料力学特性的本构模型是面板坝应力变形分析的重要内容。面板坝中的堆石材料属于无黏性粗粒土,在剪切的过程中表现出明显的剪胀性和高度非线性等力学特征[1]。堆石料在低围压下常表现为剪胀,在围压较大时呈现剪缩状态。因此,同时考虑剪胀剪缩性的堆石料本构模型能够更好地反映面板堆石坝强度和应力变形的特性。
岩土类材料本构关系没有统一的理论理解,各学者针对不同的力学特性对本构模型作出各种假设及改进。沈珠江曾指出,面板应力变化情况主要受堆石料的剪胀剪缩性的影响,因此基于新的硬化理论提出双屈服面弹塑性模型(南水模型)[2]主要用于无黏性材料剪胀特性的描述,克服非线性模型中未考虑材料的剪胀性等缺点。Rowe[3-4]基于试验研究认为剪胀性是由于颗粒材料几何内部相互约束造成的,因此提出应力剪胀理论。Wan等[5]在Rowe研究成果的基础上,考虑临界孔隙比的影响引入孔隙率相关因子,认为材料密度和应力水平也会影响颗粒剪胀特性。
目前在描述堆石料力学特性方面,贾宇峰等[6]、米晓飞等[7]和刘萌成等[8]基于试验成果考虑堆石材料的颗粒破碎和湿化变形效应,并提出相应的经验公式。刘萌成等[9]通过研究堆石材料的状态量对材料剪胀特性的影响,提出了材料压缩试验后期变形中剪胀剪缩性转化变形的相关判断准则。还有研究表明[10],在堆石料中不同分区特性各异,垫层料和过渡料在低围压下由较小的剪缩迅速转化为剪胀,在高围压下经过一段时间的剪缩,之后显现轻度的剪胀。主堆料和次堆料在剪切的过程中总体表现为剪缩性。可见,虽然关于土体剪胀性的研究成果较为丰富,但以Rowe应力剪胀方程为研究对象,对本构方程进行改进以及探讨方程在面板堆石坝中的适用性仍有研究空间。
本文首先介绍南水模型,其次将Rowe应力剪胀方程的基本公式进行了改进。然后利用改进的方程替换南水模型中切线体积比表达式,并拟合改进模型体积应变的曲线效果。最后将修正的南水模型有限元程序用于福建仙游抽水蓄能面板堆石坝上库主坝的应力变形分析,与原南水模型的有限元计算成果对比验证。
1 南水模型及其不足
南水双屈服面模型中假定双屈服面可由下列两个屈服函数组成[2]:
(1)
(2)
其中:p为平均主应力;q为广义剪应力;r和s为两个参数,堆石料中取值为2。当采用正交流动规则时,弹塑性应力变形产生的应变增量可表示为:
(3)
式中:[D]为弹性模量矩阵;A1与A2为对应屈服面f1与f2的塑性系数。
在常规三轴试验中定义:Et=Δσ1/Δε1为切线模量,μt=Δεv/Δε1为切线体积比,A1与A2可用下式表达:
(4)
南水模型中仍然采用邓肯-张模型中假定偏应力(σ1-σ3)与轴向应变ε1为双曲线关系[11],切线模量的表达式写为:
(5)
然而对于体积应变εv与轴向应变ε1之间的描述改用抛物线关系,因此切线体积比的表达式为:
(6)
式中:c、φ、Rf、K、n、S1、Cd、nd、Rd均为双屈服面模型试验参数。
南水模型中将模型常数Rd作为剪胀和剪缩的分界点,以此表现土体材料在外力作用下的剪胀剪缩性。但面板坝的堆石料种类不唯一,张丙印等[13]在研究中发现,南水模型未考虑堆石料中颗粒的体积变形机理,对部分筑坝材料的拟合效果不佳。本文利用三轴试验参数见表1。

表1 南水模型参数结果[8]
2 针对堆石料南水模型的改进
2.1 Rowe剪胀方程的改进与应用
Rowe认为影响粒状材料强度的主要因素有:颗粒材料填充孔隙重组过程中产生的能量损失、颗粒材料之间的滑动所克服的摩擦阻力以及体积膨胀过程需要的能量。由此在对粒状介质细观组构特性进行分析的基础上,抽象出一个简化的细观组构模型,通过研究粒状材料间的微观性质,应用最小能比原理建立本构模型,反映粗粒土应力与剪胀间的关系。基本思想可表述为:假定在一个圆柱形土体模型的垂直断面上,用断面上下两个刚性楔块在它们的分隔面上进行来回滑动来模拟密砂滑动的情况,另外假定分隔面之间的接触面为锯齿形,如图1所示。
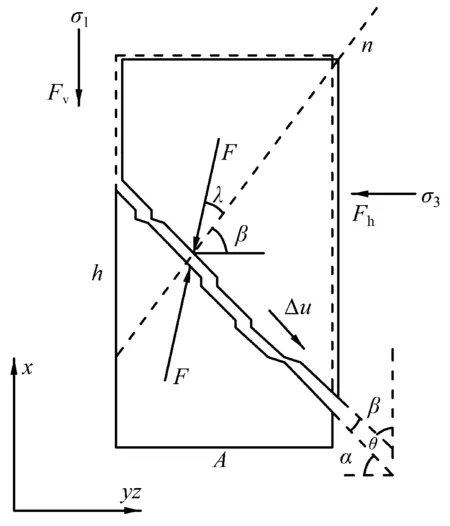
图1 圆柱形土体模型分隔面受力分析[12]
图1中,将h和A分别定义为圆柱体的高度和横截面积;在常规三轴试验条件下,σ1为垂直向应力,σ2=σ3为水平径向应力;分隔面与与小主应力σ3之间的夹角定义为α,锯齿面与与大主应力σ1之间的夹角定义为β,由于σ1与σ3相互垂直,分隔面与锯齿面间形成的偏差角θ=α+β-1/2π,当θ为正值时,滑动将引起土体体积膨胀。
平衡条件下,Fv和Fh为F的垂直和水平分量,所对应的投影面积为A和Atanα,F与n线夹角为λ,则F的水平倾角为β+λ,即可表示为:
(7)
因此,应力比表达式为:
(8)
变形相容条件下,假定分隔面产生相对位移Δu,则应变增量比为:
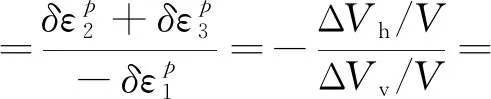
(9)
依据上述两个条件,Rowe剪胀方程可以写为:
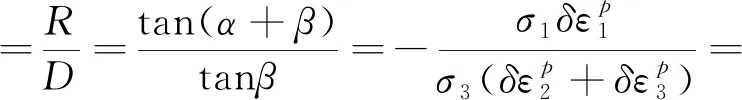
(10)
式中:Ku表示σ1与σ3所做的功之比;φcv为土体处于剪胀剪缩临界状态时的摩擦角。
根据Rowe模型中假定为刚性楔块的滑动,忽略产生的弹性变形有:
(11)
令Ru为堆石料极限状态下的应力比,对应φcv可得:
(12)
从而式(11)可简化为:
(13)
张丙印等[12]根据式(13),通过大量的堆石体常规三轴压缩试验中得出的拟合结果均在试验点数据的上方,会过高的估计粗粒土的剪胀。基于此,张丙印等在式(13)的基础上引入一个系数α,改进后的Rowe剪胀方程为:
(14)
由式(11)和式(14)可得:
(15)
因此,根据三轴试验数据拟合lg(1-dεv/dε1)-lgR的线性关系,即可确定参数α与Ru的值。
本文采用张丙印等改进的Rowe剪胀方程,对福建仙游抽水蓄能电站面板堆石坝坝体填筑料静力特性研究[13]试验数据进行拟合分析。如图3的体积应变与轴向应变拟合曲线可得,张丙印等改进的Rowe剪胀方程对于在三轴试验中表现出剪缩性的主堆料和次堆料,能够基本反映体积应变εv和轴向应变ε1之间的曲线特征。但对于垫层料和过渡料这类剪胀性材料,体积应变曲线的拟合效果并不理想。特别是在高围压条件下,改进模型的拟合值比试验值偏大较多。
本文在面板堆石坝坝体填筑料应力应变关系的拟合中发现参数α对应力比R的大小和材料剪胀性的变化较为敏感,而与极限应力比Ru的相关性较小。因此本文对剪胀方程进行如下改进:
(16)
由式(11)和式(16)可得:
(17)
依据上式,通过三轴试验数据拟合ln(1-dεv/dε1)-R的线性关系,斜率和截距为参数α和Ru。
为此,建议将式(6)中南水模型μt的表达式替换为本文改进后的Rowe剪胀方程式(16),也能使表达形式和参数求取更加简便。
2.2 改进的南水模型数据拟合验证
本节采用改进的Rowe剪胀方程求取南水模型中的切线体积比μt,对福建仙游抽水蓄能电站面板堆石坝筑坝材料的常规三轴试验数据进行拟合分析。将张丙印等改进与本文改进的Rowe剪胀方程进行对比,验证改进后模型对堆石料剪胀剪缩性的拟合效果。即将南水模型中影响体积应变的参数Cd,nd,Rd替换为改进参数α和Ru,其他参数保持不变,张丙印等与本文改进的Rowe剪胀方程参数结果见表2。
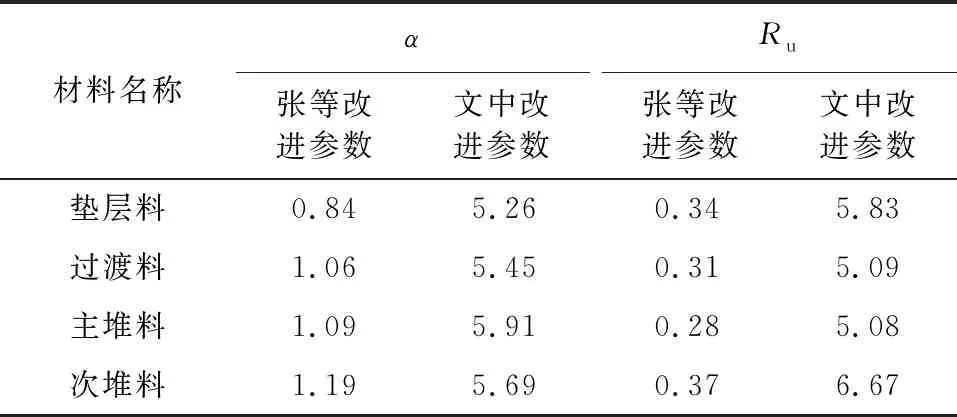
表2 改进的南水模型参数结果
通过分析不同堆石料体积应变与轴向应变关系可知,本文改进的南水模型拟合效果总体有较好的改善,体现在以下两点:(1) 与原南水模型相比,改进模型能体现主堆料和次堆料剪缩性,在不同围压情况下模型拟合值均能更好地与试验值相吻合;(2) 张等改进模型和本文改进模型,在垫层料和过渡料体应变拟合曲线中表现出材料在三轴试验后期出现剪胀的趋势,本文改进方程曲线拟合值与试验值更为接近。
综上可知,在相应围压下,改进模型的计算值与试验值拟合效果明显改善,因此采用本文中改进的Rowe剪胀方程替换南水模型中的切线体积比μt是合理可行的。
3 改进的南水模型在面板堆石坝中的应用
3.1 工程概况
本文以福建仙游抽水蓄能电站上库混凝土面板堆石坝为计算实例。上水库混凝土面板堆石坝坝址处于河域的转弯段,呈“V”型,上水库正常蓄水位为741.0 m,坝顶高程为747.6 m,最大坝高为72.6 m,防浪墙高度为1.2 m,大坝总长为340.0 m,坝顶宽8.0 m,前坡坡比为1.0∶1.4,后坡坡比为1.0∶1.8,后坡马道设置1级,宽度为2 m。混凝土面板作为主体挡水材料,从坝顶至底部逐渐从0.3 m过渡到0.5 m,面板设有分缝和止水片,隔12 m设置垂直缝,同时面板和址板之间设有周边缝。坝体依据填筑材料划分为:垫层区、过渡区、主堆区、次堆区,具体分区情况见图2。
3.2 计算情况及材料参数
在三维非线性有限元程序中,面板与垫层,趾板与堆石料之间设置无厚度的Goodman单元作为接触面单元,面板的周边缝与垂直缝也采用无厚度的Goodman作为接缝单元。接触面单元采用四川大学试验研究的材料参数,如表3所示。接缝单元的模型与参数采用河海大学“七五”科技攻关的试验成果[14]。

表3 接触面单元材料参数
坝体三维有限元网格结点总数为13 171,单元总数为11 982,坝体单元网格剖分情况如图3所示。
结合实际情况,模拟了面板堆石分层施工和蓄水。本文中分别采用自编南水模型和改进的南水模型三维有限元程序进行数值模拟[15]。
3.3 有限元计算成果
3.3.1 坝体应力变形计算成果分析
根据南水模型和本文改进的南水模型对混凝土面板堆石坝竣工期和正常蓄水期进行坝体应力变形模拟,计算的主要成果见表4、图4—图7。
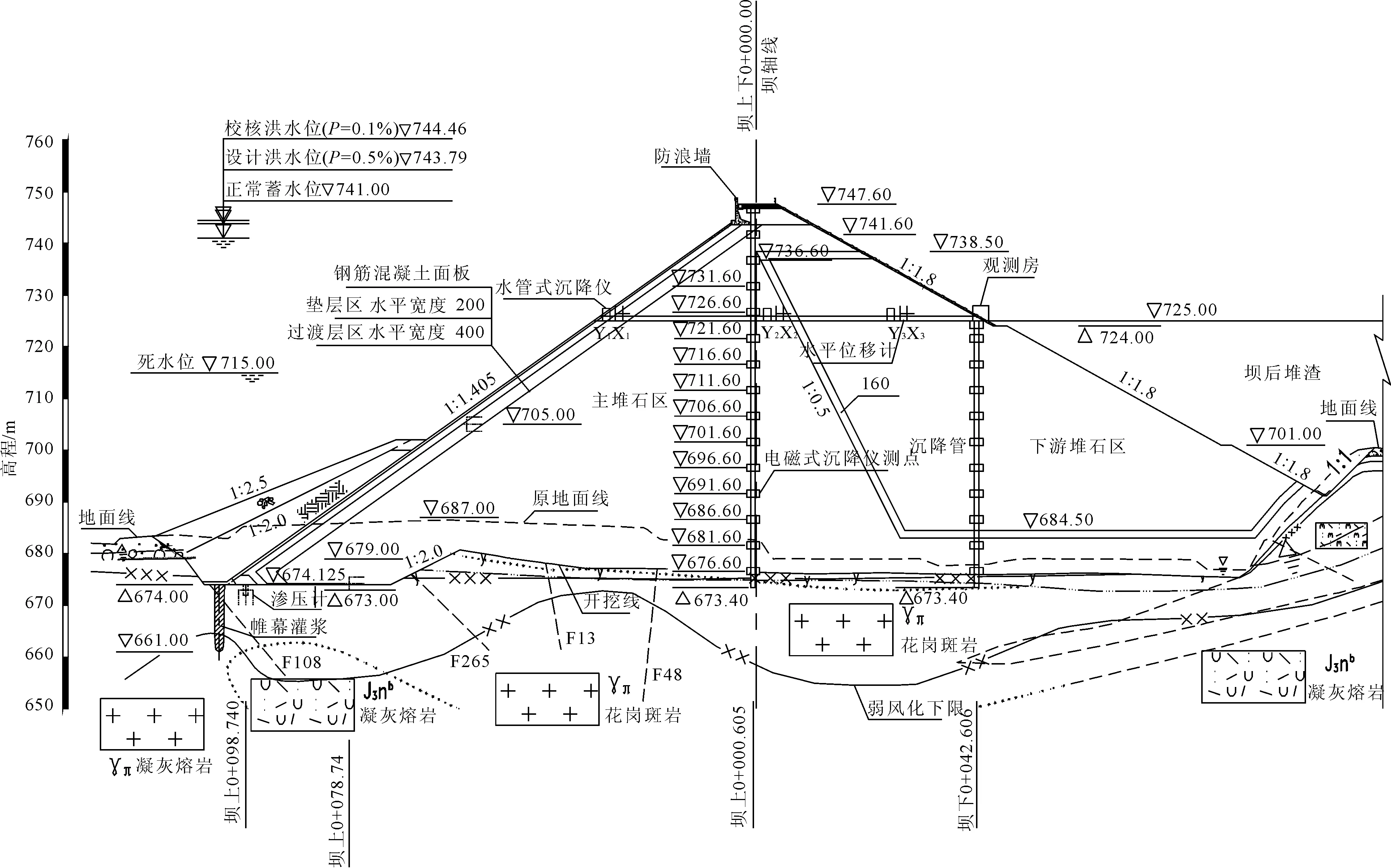
图2 福建仙游抽水蓄能电站上水库主坝剖面图
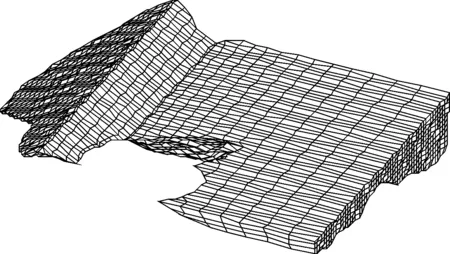
图3 上库面板坝有限元网格
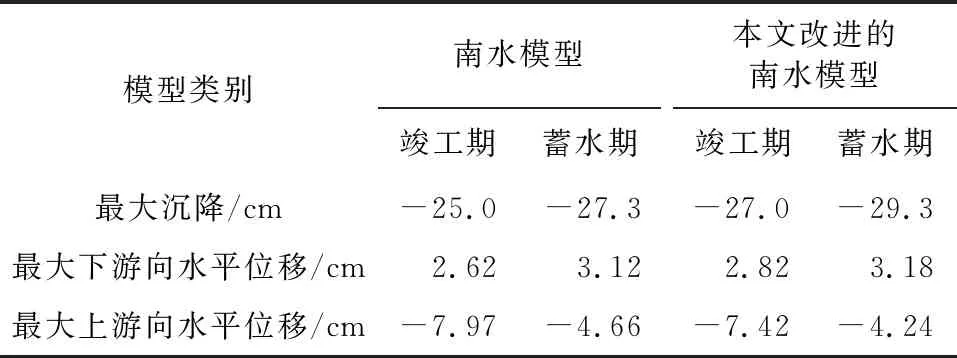
表4 坝体应力变形计算结果
由图5可知,坝体最大沉降出现约在坝体的1/2高程处,南水模型和改进的南水模型计算的最大沉降值分别为25.0 cm和27.0 cm,分别约占坝高的 0.34%和0.37%,并且坝体沉降分布规律一致。
在坝体自重的作用下,竣工期将产生侧向的水平位移,由图6可知,坝体水平位移关于坝轴线对称。实际工程中坝体侧向变形主要表现为下部坡面朝外鼓出,上部坡面朝内收缩。两种改进模型的水平位移等值线结果较为相似,南水模型与改进的南水模型最大下游向位移的计算值分别为2.62 cm和2.82 cm,最大上游向位移分别为7.97 cm和7.42 cm。
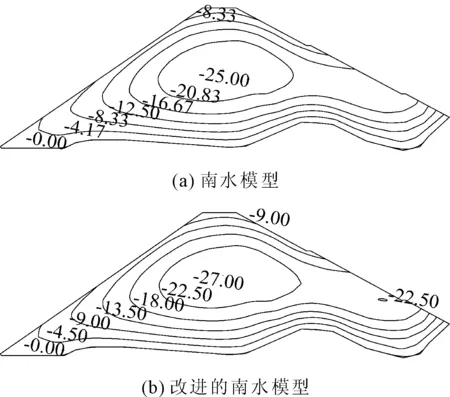
图4 竣工期河床断面垂直位移(单位:cm)
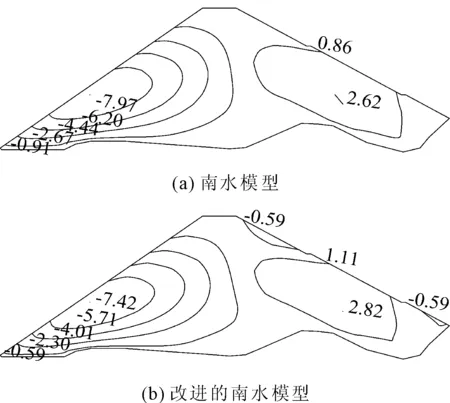
图5 竣工期河床断面水平位移(单位:cm)
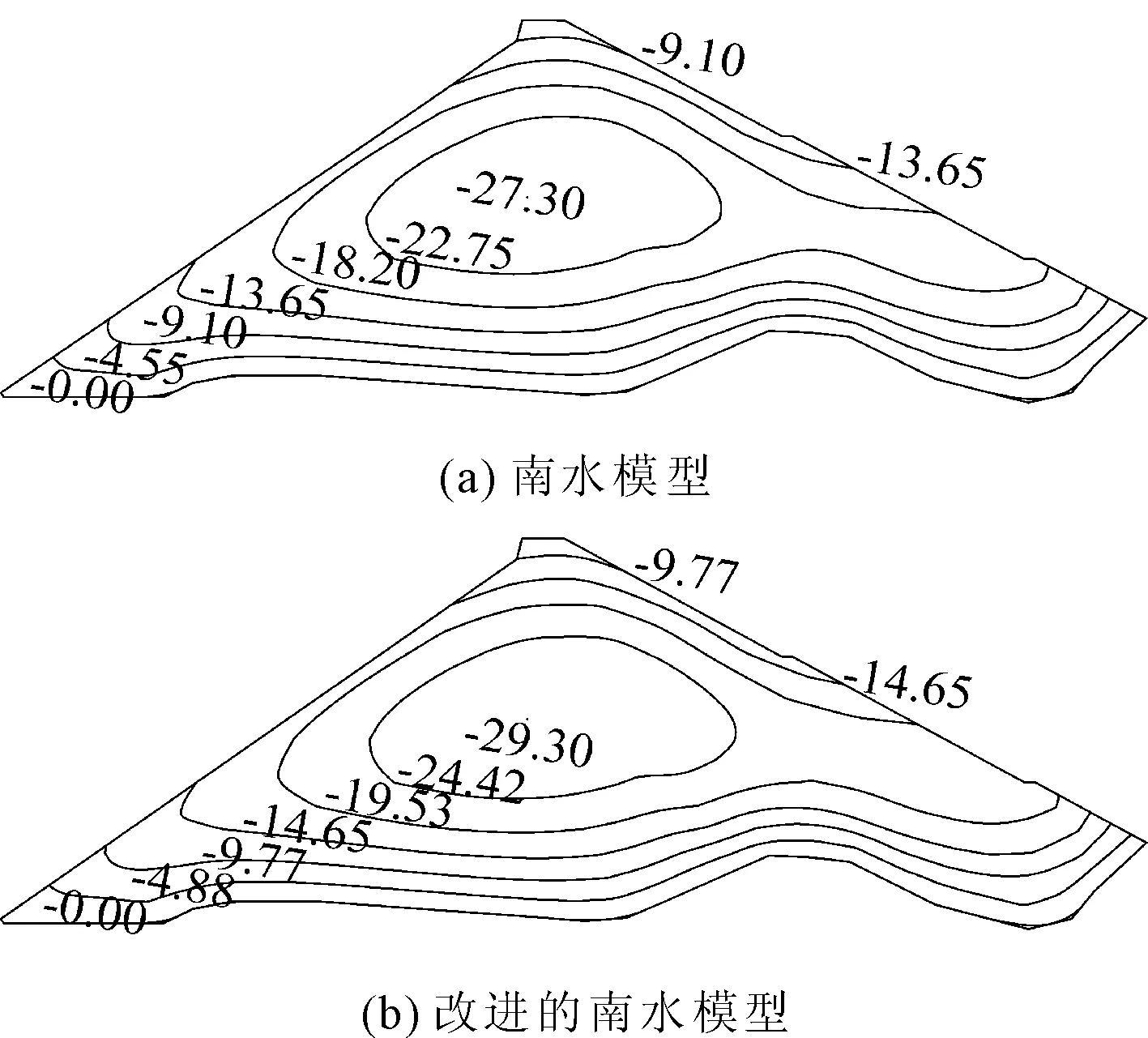
图6 蓄水期河床断面垂直位移(单位:cm)
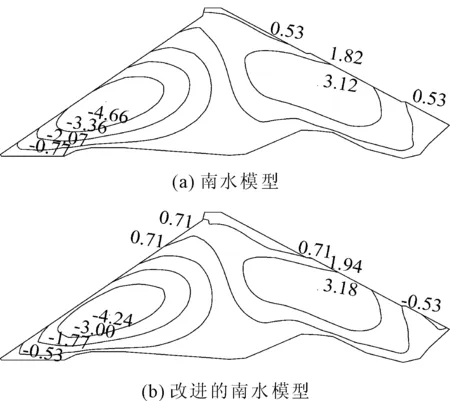
图7 蓄水期河床断面水平位移(单位:cm)
分析两种模型坝体垂直位移的模拟情况,将竣工初期坝轴线处的沉降管1(坝0+150.33断面坝上0+0.605)和坝下游次堆料处的沉降管2(坝0+124.046断面坝下0+042.606)两处的监测值和相应测点的模拟值进行对比(各测点布置见图2)。沉降量数据对比结果如图8所示,南水模型和改进模型所表现出的坝体沉降趋势相似,本文模型计算结果与监测值拟合更好。除两端测点外,其余测点的改进模型计算值和实测值相差在24.7%以内。
3.3.2 面板应力变形计算成果分析
蓄水时面板作为水压力的直接承载体,其应力变形情况是大坝稳定分析的重要参考指标。南水模型和本文改进的南水模型蓄水期面板应力变形计算成果见表5。规定面板挠度以法向位移指向坡面内法向为正,应力以压为正,反之为负。
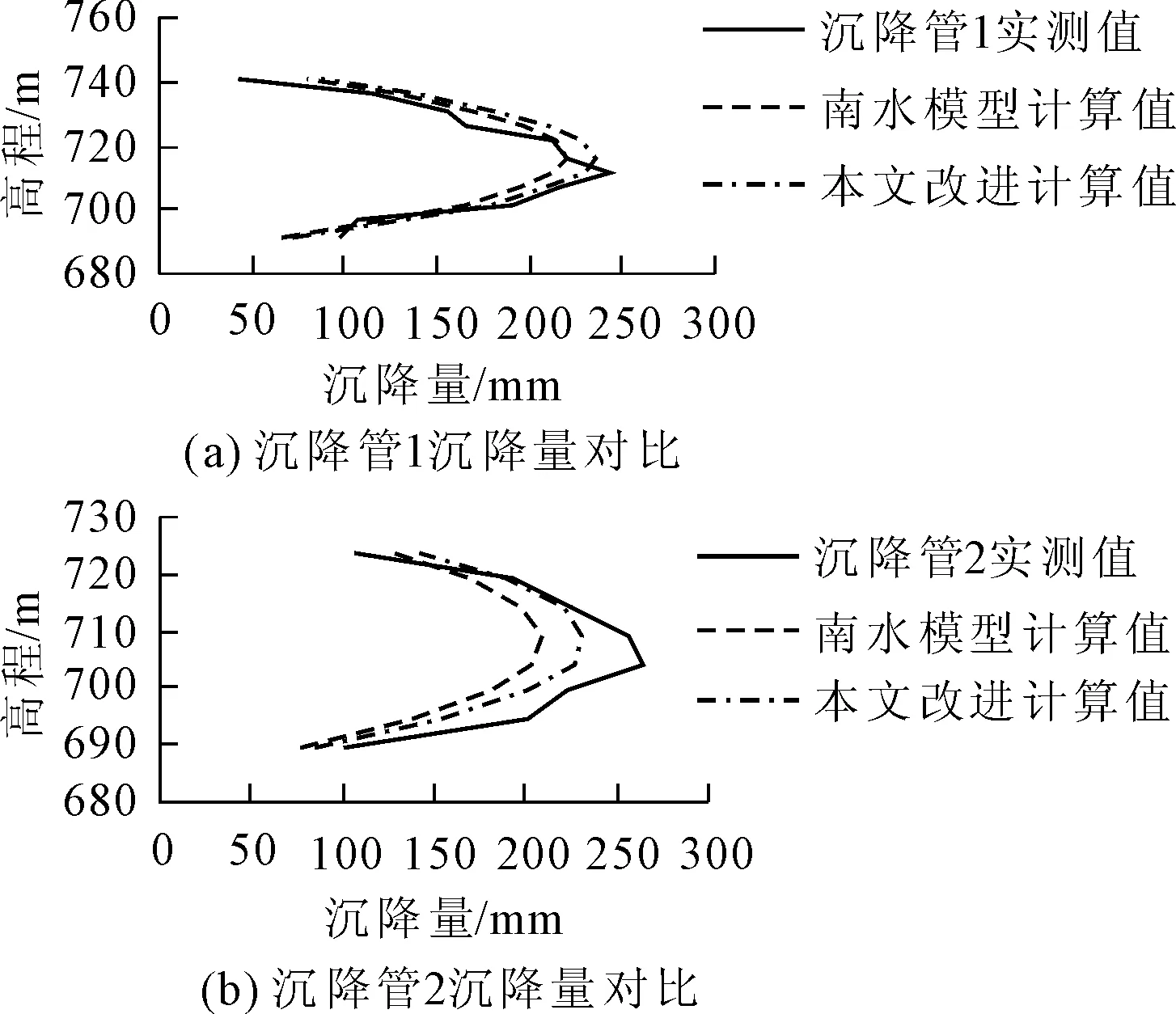
图8 竣工期垂直位移模拟与实测值对比
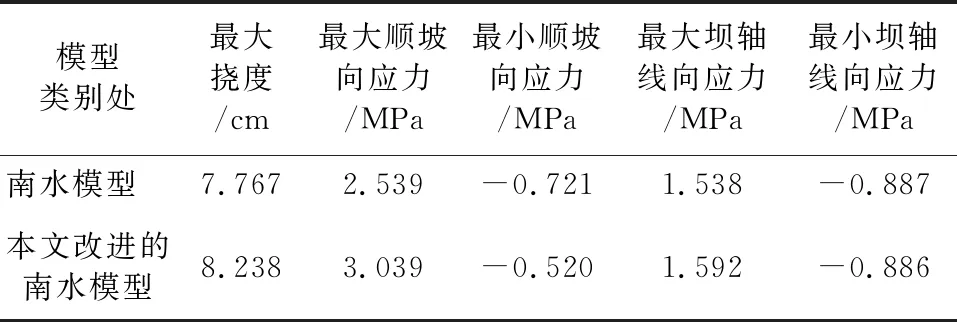
表5 蓄水期面板应力变形计算结果
面板在水压力的作用下,挠度指向坡内法向方向,最大值出现于面板中部偏下约1/3坝高处,并呈现从极值处往四周递减趋势。南水模型和改进的南水模型计算的蓄水期面板挠度最大值分别为7.767 cm和8.238 cm。工程中要求面板具有一定的柔性,以适应堆石料的变形,改进后的模型挠度有更大的安全裕度。
在蓄水期工况时,面板沿顺坡方向因水压力作用,引起面板的弯曲变形。原模型和改进模型计算的压应力最大值位于面板的中下部,分别为2.539 MPa和3.039 MPa。此外,拉应力区大部分位于面板底部或者顶部,但拉力值不大,最大值分别为0.721 MPa和0.520 MPa。
在蓄水期工况时,面板沿坝轴线方向也主要承受水压力作用,压应力最大值位于面板的中部,原模型和改进模型计算值分别为1.538 MPa和1.592 MPa。在两岸与山体接触区域处于受拉状态,最大值位于左岸底部,分别为0.887 MPa和0.886 MPa。
从以上两种模型的有限元计算成果讨论可知,模型计算的垂直位移、水平位移、面板挠度、顺坡向应力和坝轴线向应力等分布规律大致相同。竣工期改进模型的沉降量更接近实测值,改进模型的位移和应力变形量略大于原模型,表明了改进的南水模型适用于面板堆石坝的应力变形分析,且有较大的安全裕度。
4 结 论
(1) 利用改进的 Rowe 剪胀方程计算南水模型中切线体积比,修正了南水模型中体积应变与轴向应变之间的关系,拟合结果与原南水模型有较大的改善。尤其是在垫层料和过渡料的模拟中,改进后的模型更能体现其剪胀剪缩性。
(2) 利用三维非线性有限元程序对工程实例进行应力变形计算,改进模型和原模型计算成果相近,能够反映堆石料的主要力学特性且有更大的应力变形安全范围。今后有待于扩大验证范围,对改进公式作更进一步尝试。

