波浪荷载作用下饱和珊瑚砂动强度特性研究
申春妮,余咏平,方祥位,姚志华,李晶鑫
( 1.重庆科技学院 建筑工程学院, 重庆 401331; 2.陆军勤务学院 军事设施系, 重庆 401311;3.重庆大学 土木工程学院, 重庆 400045; 4.空军工程大学 机场建筑工程系, 陕西 西安 710038)
珊瑚砂,又称为钙质砂,是广泛分布于海洋大陆架和各类岛礁的一类不同于普通陆源砂的岩土材料,主要分布在南北回归线之间的热带海洋中,形成过程受海洋潮汐、波浪、海流影响,由于生物沉积作用,其主要成分为碳酸钙,占比达90%以上[1-4]。现代海洋资源开发和各类岛礁工程建设,使得作为承载地基的珊瑚砂处于复杂应力状态,珊瑚砂的动力特性成为研究热点。
近年来,国内外学者通过多种室内试验研究了珊瑚砂的动力特性,取得了一定成果。Morrisno等[5]通过循坏直剪和扭剪试验,发现对于南非沿海产地相同而含有不同碳酸钙的珊瑚砂,在体积相同和应力一致的情况下,珊瑚砂碳酸钙含量越高,动强度下降越明显,对同一种珊瑚砂,循环荷载下剪缩现象是造成其动强度降低的主要因素。AI-Douri等[6]通过循环直剪试验发现,珊瑚砂剪应力与正应力、孔隙比、水平位移、粒径和颗粒形状有关,其大小及变化速率随循环次数增加而减小。Catano等[7]通过共振柱试验发现在相似的相对密实度和围压下,珊瑚砂剪切模量低于硅砂,珊瑚砂受围压影响变化程度大。李建国[8-9]使用先进的土工静力-动力液压三轴-扭剪多功能剪切仪,模拟波浪荷载作用下的钙质砂受力状态,研究发现:当初始主应力方向角减小时,钙质砂动强度增强,变化规律为非线性;中主应力系数变化也能改变钙质砂动强度大小,影响程度小于初始主应力方向角。虞海珍[10]通过系列循环剪切试验,得出以下结论:饱和钙质砂的动强度与振次有关,大小随振次增加而减小;均压固结条件下钙质砂的动强度随着初始平均有效固结压力的增大而增大;珊瑚砂在非均压固结时,初始主应力方向角和初始偏应力对动强度影响显著,对中主应力系数b值影响较小;对循环三轴试验、循环扭剪试验和循环耦合试验而言,前者动强度远大于后两者,而后两者相差不大。李晶鑫等[11]通过空心圆柱扭剪试验模拟不同频率的波浪荷载,考虑中主应力系数变化,使应变分布更加均匀,研究饱和珊瑚砂孔压和竖向应变发展规律,发现当波浪荷载循环频率升高时,饱和珊瑚砂孔压和振次的幅值近似线性增加。
综上所述,国内外学者对珊瑚砂的动力特性进行了较为深入地研究,珊瑚砂在波浪荷载作用下的动力特性研究已取得初步成果,但其研究仍不够全面和深入,没有考虑主应力轴旋转频率的影响。本文针对岛礁陆域吹填珊瑚砂,利用动态空心圆柱扭剪仪HCA-100进行不同条件下的空心圆柱扭剪试验,研究波浪荷载加载频率和珊瑚砂相对密实度对饱和珊瑚砂动强度特性的影响,丰富珊瑚砂动力学特性研究成果。
1 试验设备与试验方法
1.1 试验设备
试验所用仪器为美国GCTS公司生产的HCA-100型空心圆柱扭剪仪,可进行常规三轴及动三轴试验,能够进行静、动扭剪试验,能实现常规动、静扭剪仪所有功能。试验中通过程序控制扭矩、轴力及内外围压的变化来实现加载,4个外荷载能够独立地以三角函数、线性或三角波进行控制,能够实现较为特殊的应力路径加载。因空心圆柱试样的特性,试验得以施加扭矩且空心圆柱薄壁范围内可视为扭矩相等。当施加扭矩后空心圆柱薄壁垂直径向方向产生剪应力,平行于薄壁面主应力轴方向发生偏转,满足了主应力轴旋转的试验要求,具有类似应力路径的波浪荷载、车辆荷载的试验模拟更符合实际,因此空心扭剪仪广泛应用于高标准的岩土试验中。仪器主要技术指标如表1所示。

表1 仪器主要技术指标
1.2 试验材料
珊瑚砂取自南海某岛礁,试样颗粒粒径小于2 mm,相对密度为2.76,碳酸钙含量为95.6%,最小干密度ρdmin=1.14 g/cm3,最大干密度ρdmax=1.43 g/cm3,最大孔隙比emax=1.424,最小孔隙比emin=0.895。试样用砂通过筛分制成中砂,颗粒级配曲线如图1所示。试验制样采用灌砂法分层击实,利用通二氧化碳和施加反压使试样饱和,通过自动化程序测得饱和系数B值达0.96以上。
1.3 波浪荷载应力路径
波浪荷载在偏应力力系中表现为球应力p和偏应力q为一定值,主应力方向角连续变化。为了使空心扭剪试样的径向压力均等分布,使应变分布更加均匀,要求内外围压相等,此时b=sin2α。为便于计算,偏应力q=(σ1-σ3)/2。Hight等[12]研究表明空心扭剪试样的一般应力状态受力表达式为:
(1)
(2)
(3)
(4)
式中:σz、σR、σθ、τzθ、W、MT分别为竖向应力、径向应力、环向应力、剪应力、轴力、扭矩;ri、ro别为试验试样内外半径;Pi、Po别为内外围压。

图1 颗粒级配曲线
根据上述公式,董彤等[13]推导了空心扭剪仪上实现设计荷载的加载公式:
(5)
(6)
(7)
(8)

通过合理的设定内外围压、轴力和扭矩加载方式来实现试验需要的应力路径。一般波浪荷载应力路径在τzθ-(σz-σθ)/2平面呈圆形,根据试验数据,偏应力取30 kPa时,实际应力路径如图2所示,可见理论与试验结果基本符合,在空心扭剪仪上按上述公式加载模拟波浪荷载可行。

图2 试验应力路径
1.4 试验方案
为研究波浪荷载频率和珊瑚砂相对密实度对饱和珊瑚砂动强度特性的影响,分析建立包含波浪荷载循环频率的饱和珊瑚砂动强度发展模式,共进行了17组试验,波浪荷载频率取0.1 Hz~0.2 Hz,珊瑚砂相对密实度取30%、55%和70%,偏应力比取0.3~0.5,平均有效固结压力取100 kPa,初始主应力方向角与中主应力系数均取0、b=sin2α。试验方案如表2所示。

表2 试验方案
1.5 动强度与试样破坏标准
试样在一定的循环荷载加载周期数下达到规定的破坏标准所需偏应力即为试样在该循环条件下的动强度。本文采用空心圆柱扭剪仪模拟波浪荷载的主应力轴连续旋转,因为同时受到轴向应力与径向扭矩及内外围压的作用,应力状态复杂,偏应力与剪应力都会对试样的稳定性产生影响,故按下式来计算动强度[14],最终结果取其最大值。
(9)
式中各符号定义与常规三轴与普通扭剪试验一致,对于空心圆柱扭剪试验,上式所求得的最大剪应力幅值相当于模拟波浪广义“圆形”应力路径中圆的半径大小,数值上近似等于试验控制条件中设定的偏应力。
动荷载作用下试样破坏标准的定义,目前还存在较多分歧,常用的破坏标准包括孔压标准、屈服标准和应变标准。考虑到空心扭剪试验中轴向应变和剪应变的影响,本文采用广义应变作为试样破坏标准[14],即当广义剪应变γg达到5%时视为试样破坏,计算公式如下:
(10)
式中:ε1、ε2、ε3分别为大、中、小主应变。
2 试验结果与分析
2.1 波浪荷载加载频率对饱和珊瑚砂动强度特性影响
图3为珊瑚砂相对密实度为55%,有效固结压力100 kPa,当偏应力比分别为0.3、0.4和0.5时,波浪荷载作用下试样破坏所需荷载循环次数与荷载加载频率关系图。由图可知,当破坏偏应力比一定时,饱和珊瑚砂破坏所需波浪荷载循环振动次数随着波浪荷载加频率增大而增大。当破坏偏应力为30 kPa时,饱和珊瑚砂试样破坏所需波浪荷载循环次数随加载频率的变化极为明显,但随着偏应力比的增加,只需要很少的循环振动次数饱和珊瑚砂试样就已经破坏,说明低偏应力比条件下,试样破坏所需荷载循环次数更易受波浪荷载加载频率的影响。
图4为珊瑚砂相对密实度55%,平均有效固结压力为100 kPa,波浪荷载循环频率f分别为0.100 Hz、0.125 Hz、0.150 Hz、0.175 Hz和0.200 Hz时对应的动强度与破坏振次关系曲线。从图4可以看出,不同荷载加载频率下的试样破坏时的广义剪应力与循环荷载振次基本呈负相关,随着振动次数的增加饱和珊瑚砂试样破坏广义剪应力下降,符合一般规律。随着加载频率增大,动强度曲线在图中自左下而右上排列,说明破坏广义剪应力随着波浪荷载加载频率的增大而增大。不同波浪荷载加载频率的动强度曲线基本平行排布,说明波浪荷载加载频率对动强度随振次影响变化的规律基本没有影响。随振次增加, 同循环荷载频率的动强度曲线按照频率由小到大的顺序,在图4中从左下到右上排列,说明随波浪荷载加载频率增加,饱和珊瑚砂破坏时所需的波浪荷载循环振动次数也相应增加,与图3结果一致。
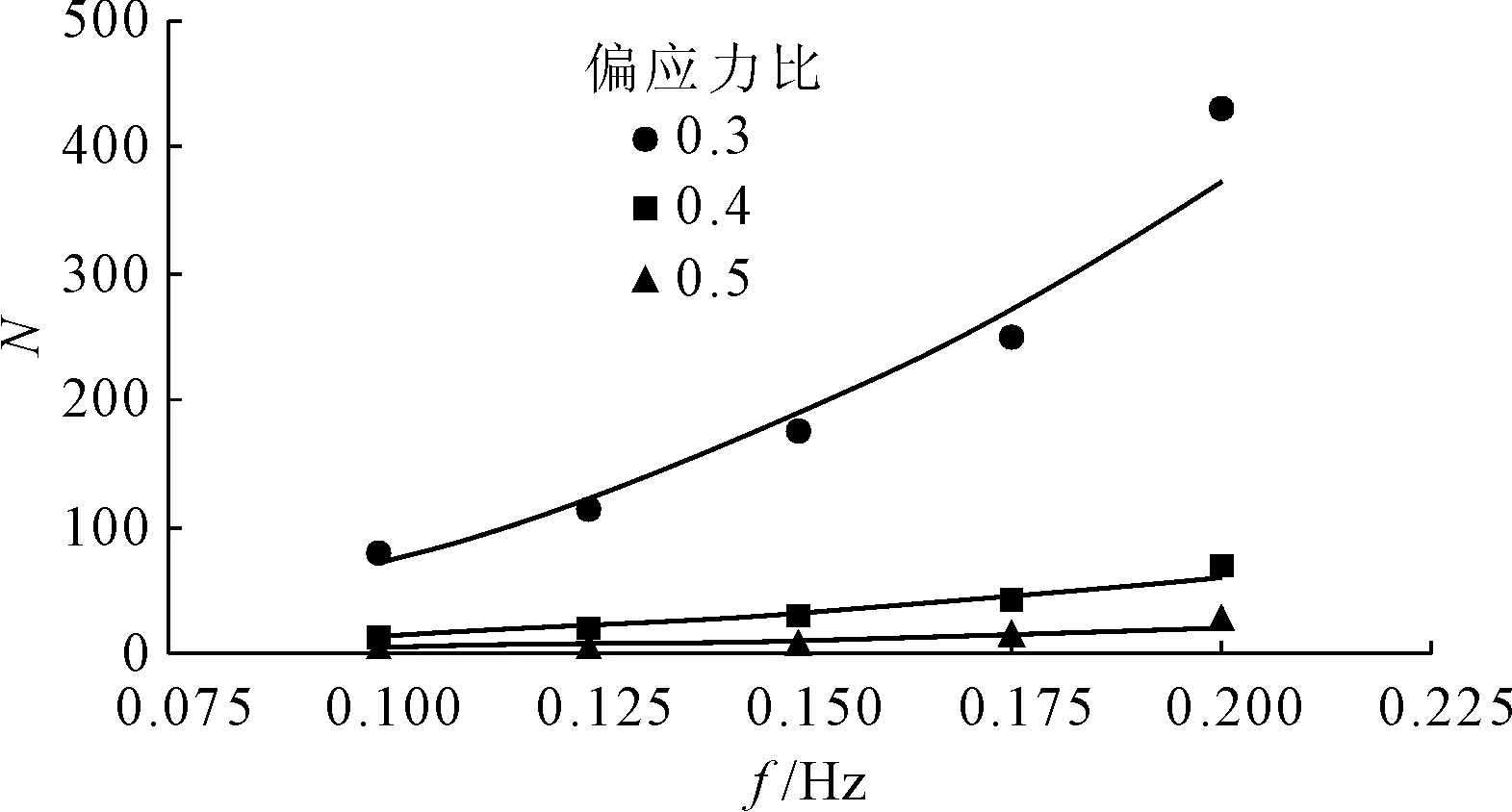
图3 破坏振次与荷载频率关系曲线(不同偏应力比)

图4 动强度与破坏振次关系曲线(不同荷载频率)
图5为破坏振次N=30、50、70条件下,饱和珊瑚砂动强度与荷载加载频率关系曲线。

图5 动强度与荷载频率关系曲线(不同破坏振次)
由图5可以看出,在不同破坏振次条件下,随着荷载加载频率的增长,饱和珊瑚砂的动强度都呈现出上升的趋势。并且不同破坏振次条件的曲线基本平行排列,表明破坏振次对动强度随荷载循环频率的发展规律基本没有影响。由图可知,当波浪荷载加载频率为一定值时,随着破坏振次的增加,试样的动强度随之降低。产生这一现象的主要原因是循环加载应力路径中存在的剪应力可以在每个循环中不断地消除不规则珊瑚砂颗粒之间的咬合,动强度降低。
表3给出了不同破坏振次N=30、50、70条件下,不同荷载加载频率对应的珊瑚砂动强度及其与荷载加载频率f=0.1时的动强度相比增加的百分比情况。从表中可以看出,当荷载加载频率由0.1 Hz增加到0.2 Hz时饱和珊瑚砂动强度增加34.3%~36.4%。郭莹等[15]曾对陆源硅砂进行动三轴试验,研究荷载加载频率对饱和砂土动强度的影响,得到在0.05 Hz~1.00 Hz荷载加载频率范围内砂土动强度随着荷载加载频率的增大而增大。由此可知,荷载加载频率对饱和珊瑚砂和饱和硅砂的动强度影响具有相似规律。

表3 荷载循环频率对珊瑚砂动强度的影响
2.2 相对密实度对饱和珊瑚砂动强度特性影响
图6为波浪荷载循环频率f=0.15 Hz,平均有效固结压力为100 kPa,珊瑚砂相对密实度分别为30%、55%和70%时的动强度与破坏振次关系曲线。从图6可以看出,不同珊瑚砂相对密实度条件下的试样破坏时的广义剪应力与循环荷载振次基本呈负相关,随着振动次数的增加饱和珊瑚砂试样动强度下降。不同珊瑚砂相对密实度条件下的动强度与荷载振次关系曲线不重合且随着珊瑚砂相对密实度的增加由左下至右上排列,故珊瑚砂动强度随着珊瑚砂相对密实度的增加而增加。

图6 动强度与破坏振次关系曲线(不同相对密实度)
2.3 饱和珊瑚砂动强度发展模式
土体动强度模式受荷载加载频率条件影响,已有学者进行了相关研究[16-17]。理论上,考虑波浪荷载循环频率的动荷载模式应该同时考虑到频率与振次的影响,但变量的增加会使模型变得复杂。不同荷载加载频率条件下所对应动强度曲线基本平行,假定不同荷载加载频率条件下所得动强度较荷载加载频率为0.1 Hz条件下所得动强度上升的情况不受振次的影响。假定Nf=10时,将不同荷载加载频率条件下与0.1 Hz时的循环应力比之差,作为建立包含荷载加载频率动强度模式的依据。
图7为不同荷载加载频率条件下的q/p′-q0.1/p′—f关系曲线。由图可知,不同荷载加载频率对应的q/p′-q0.1/p′—f关系曲线可以用函数K(f)较好的拟合,即在荷载加载频率为0.1 Hz~0.2 Hz范围内任一荷载加载频率所对应的循环应力比q/p′与荷载加载频率为0.1 Hz所对应的循环应力比q0.1/p′之间的关系可以用下式表示:
q/p′=q0.1/p′+K(f)
(11)
式中函数K(f)=Af2-Bf+C,A、B、C为试验参数见表4。又由图7可以发现q0.1/p′与荷载加载周期数N呈负乘幂关系,故q/p′可以表示为:
q/p′=DNE-K(f)
(12)
式中:D、E为试验参数,具体数值见表4。经验公式(12)可较好的反映荷载加载频率对饱和珊瑚砂动强度的影响。
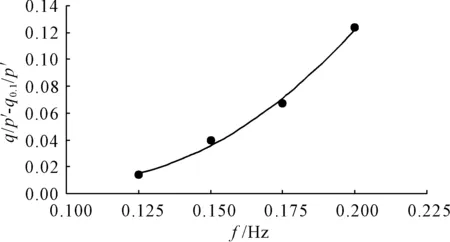
图7 q/p′-q0.1/p′—f关系曲线

表4 试验参数
3 结 论
采用HCA-100型空心圆柱扭剪仪,试验模拟波浪荷载作用下饱和珊瑚砂的动应力应变过程,研究了波浪荷载加载频率和珊瑚砂相对密实度对饱和珊瑚砂动强度的影响规律,得出以下几点结论:
(1) 试样破坏所需荷载循环次数随波浪荷载加载频率增加而增加,在低偏应力比条件下更为明显;相同加载频率下,饱和珊瑚砂动强度随破坏循环次数增加而减小;波浪荷载作用下饱和珊瑚砂动强度随荷载加载频率增大而增大。
(2) 波浪荷载作用下饱和珊瑚砂动强度随着珊瑚砂相对密实度增大而增大。
(3) 根据不同荷载加载频率下饱和珊瑚砂对应的偏应力比与初始荷载加载频率为0.1 Hz时的偏应力比之间的关系,建立了考虑荷载加载频率的饱和珊瑚砂动强度经验公式。

