基于二自由度的垂直冲击试验机参数设计计算方法

徐曼

（苏州世力源科技有限公司，苏州 215337）

引言

当前，冲击力学环境试验技术是考核产品在工作或运输过程中安全性及可靠性的主要方式之一，而垂直冲击试验机则是最常使用的实现经典冲击力学环境试验各项指标主要设备之一。该设备不仅适用于各类民用产品的运输考核，也广泛用于航天、航海等军工产品的性能考核[1]。垂直冲击试验机的型号多种多样，不同型号的垂直冲击试验机可以模拟出不同规格的冲击波形，但各类垂直冲击试验机的结构类似，均可用同一类模型模拟其工作原理，并得出其测试参数，即垂直冲击试验机台面的跌落高度和波形发生器的刚度。图1展示了一个典型垂直冲击试验机的结构简图。

目前，对垂直冲击试验机的参数计算主要基于单自由度弹簧-质量模型，并且忽略了重力，底座以及气囊等工况结构[2]。该模型过于简单，计算出的跌落高度、波形发生器刚度等参数精度较低，大多需要依靠人工经验纠正误差，不能很好地指导冲击试验机的设计[3]。部分研究者虽然利用泰勒公式和最小二乘法拟合垂直冲击试验机测试参数的经验公式，并通过试验数据归纳总结相关系数，形成经验数据库，但该计算方法过分依赖经验，有很大的局限性和盲目性[4]。

本文考虑垂直冲击试验机的底座阻尼器、缓冲气囊的影响，建立更加精确的二自由度动力学模型来模拟垂直冲击试验机的工作情况。通过四阶龙格库塔方法求解此动力学方程组的数值解，得到满足要求的冲击波形的离散值。在求解过程中，使用一维搜索方法(二分法)不断矫正所需的冲击波形，迭代计算出满足要求的波形指标，并绘出冲击波形图。同时，通过缓冲气囊的力位移曲线，得出冲击试验机底座对地基的最大冲击力，以便设计和调试冲击试验机时尽量减少对地基的影响。该模型可以较准确地描述冲击试验机工作状态的动力学行为，并且针对具体的冲击波形指标，计算出理想的设计参数。最后，搭建试验平台，对计算出的理论参数进行试验对比研究，证明了此算法的准确性。

1 垂直冲击试验机的工作原理

垂直冲击试验机的工作原理是将所需测试的产品固定于工作台面上，再通过提升气缸将台面上升到指定高度，然后释放，使台面自由跌落，最后与固定在试验台上的波形发生器相碰撞，产生所需要的加速度波形，从而模拟产品遭受的冲击环境，考核产品的可靠性[5]。另外，在台面和产品上分别装有加速度传感器，从而确定产品所承受的冲击波形是否符合要求。

考核产品的冲击波形种类繁多，大致可以分为半正弦波，后峰锯齿波和梯形波。不同的波形发生器在与台面碰撞之后可以产生不同的冲击波形。半正弦波形发生器一般采用橡胶材料制成，橡胶材料具有超弹性且较硬等特性，因此通常产生的是近似半正弦波形[6]。后峰锯齿波的波形发生器主要采用铅块制成，利用铅块塑形强的特点来产生后峰锯齿波形。而梯形波的波形发生器需要采用气缸式结构，通过在一段行程内，气缸推力值不变的特性来实现梯形波形[1]。

本文主要是研究垂直冲击试验机使用参数的计算方法，不考虑波形发生器的类型，所以本文模型选取最常用的半正弦波形发生器对垂直冲击试验机的使用参数进行计算。

2 垂直冲击试验机设计参数计算

2.1 垂直冲击试验机动力学模型的建立

当前计算垂直冲击试验机的参数时，都忽略了由冲击台底座、气囊和阻尼器组成的减震系统，所以误差较大。本文为了最大限度地模拟实际情况，将垂直冲击试验机简化为二自由度系统[1,5]。

如图2所示，将工作台面简化为一质量块，质量为m1，底座简化为质量为m2的物体。考虑到气囊刚度的非线性，将其弹力等效为F(x2)，刚度为k2，阻尼器阻尼系数为c2，而波形发生器等效成刚度为k1的弹簧，其阻尼系数为c1。则冲击试验机工作台面碰撞到波形发生器后，其动力学方程为：

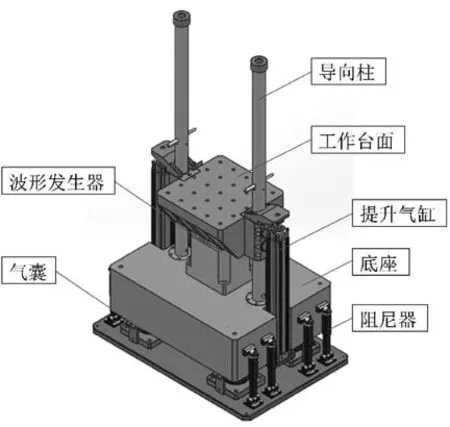
图1 垂直冲击试验机结构简图

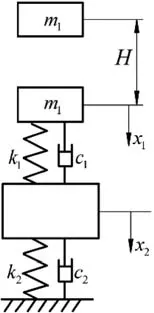
图2 二自由度动力学模型图

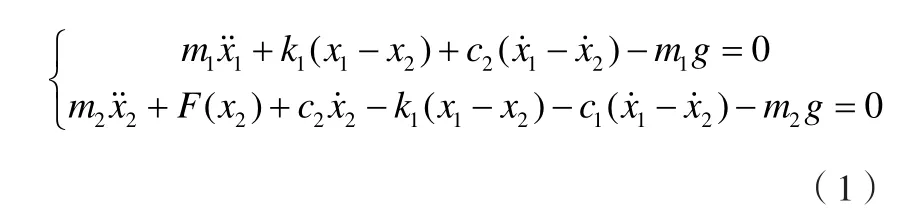
为了考虑垂直冲击试验机体对地基产生的冲击作用，选取模型中的等效弹簧、阻尼器均未压缩时的状态为坐标原点，工作台台面从距离波形发生器H的位置自由跌落。此时模型的初始条件为：

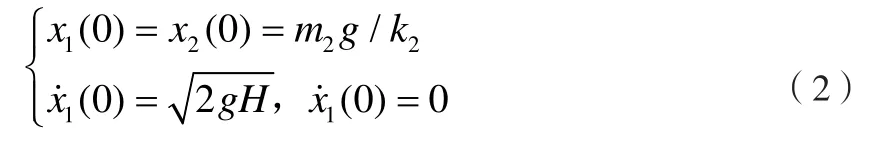
2.2 动力学方程的求解

本文采用龙格库塔法求此二自由度模型的数值解。龙格库塔方法是一种在工程上应用广泛的高精度单步迭代算法。该方法既可以采用一阶精度欧拉公式，利用微小步长两端的一阶导数平均，得到改进的二阶欧拉公式，不断迭代出步长增量的函数值，还可以通过n阶泰勒公式，舍去高阶导函数部分，与龙格库塔模型对比，得出模型的迭代系数[7]。龙格库塔法不仅具有精度高，建模方便等优点，还可以通过抑制其迭代误差，得到满足需求精度的数值解。

因为龙格库塔法精度可控，且其迭代系数多种多样，从而形成了不同形式的龙格库塔方程。而其中最常用的是四级四阶龙格库塔方程，该方法每一步需要计算四次函数值，其格式如下：

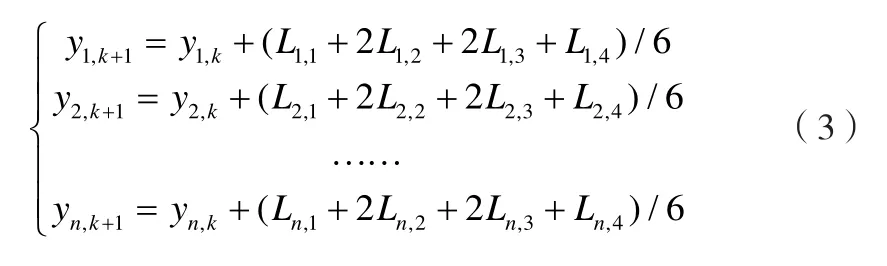
式中：

Li,n—微分方程组的增量；

h—迭代步长。

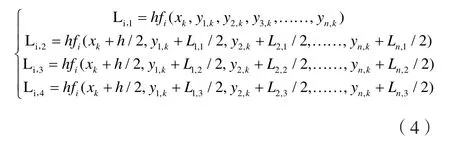
针对本文的模型，将二自由度模型的二阶微分方程组进行转换，即令

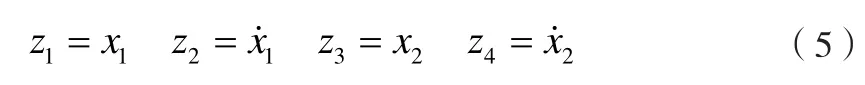
得到可用四级四阶龙格库塔法求解的形式：

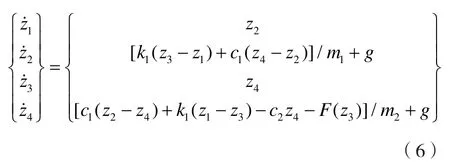
带入模型初始条件：

便可迭代得出此模型的数值解。

2.3 冲击试验机工作台面跌落高度与波形发生器刚度的计算

二分法通常用于求解函数的近似根，相比于牛顿迭代法等其他算法，该方法具有结构简单方便，迭代速度快等优点[8]。本文采用二分法，将计算出的加速度峰值和波形脉宽不断比较，对垂直冲击试验机的参数进行修正和优化。

首先，假设系统为一阶系统，可以根据加速度峰值A和波形脉宽D，确定初始跌落高度H0和波形发生器刚度k0。

将初始跌落高度和波形发生器刚度同时缩小和扩大两倍得到迭代区间，再将每次计算出的脉宽与所需脉宽比较，若脉宽较小，则减小刚度，反之亦然。对于跌落高度的修正，若峰值加速度过大，则降低跌落高度，反之亦然。最终得到所需的跌落高度和波形发生器刚度等垂直冲击试验机的关键测试参数。

为了将波形发生器刚度转化为橡胶肖氏硬度，从而便于选择或制备相应的橡胶波形发生器。如图3所示，先确定波形发生器的直径D0和高度M。根据所计算出的刚度K，得出橡胶的肖氏硬度HS。

式中：

S和G—橡胶的形状因子和剪切模量，单位为MPa。

2.4 垂直冲击试验机对地基的冲击力

通过解微分方程组，可以求出底座的位移x2，即气囊的压缩量。本文选择FESTO公司生产的气囊，型号为EP-250-85，并保证气囊内部气压为4 bar。通过气囊的弹性性能曲线和压缩量得出其所承受的载荷，如图4所示。可见，代入气囊的压缩量，即可计算出地基所受的最大冲击力。

3 垂直冲击试验机参数设计软件的实现

3.1 Lab Windows/CVI的简介

Lab Windows/CVI是由美国National Instruments公司推出的虚拟仪器软件。它是一个完全以ANSIC为核心，使用灵活的C语言平台用于数据采集、分析和显示的专业测控工具。它具有丰富的功能面板和函数库，并且采用交互式编程方法，大大增强了C语言的功能，建立了一个理想的软件开发环境[9]。

Lab Windows/CVI具有许多优点和特性。它提供了标准的函数库和交互式函数面板，用户可以利用非常便捷的界面编辑器，创建导向函数库，实现显示控制等功能。此外，Lab Windows/CVI还优化了集成编辑器，除了可以使用其自带的编译代码，还可以使用专用的Microsoft Visual C++，Borland和Intel等预先配置好的编译模板。Lab Windows/CVI最强大的功能在于它有丰富的函数库和图形用户界面，并提供了指示灯，示波器和按钮开关等常用控件，大大降低了实验成本[9,10]。工程上常使用Lab Windows/CVI完成交互式程序开发，数据采集及分析和开发IVI仪器驱动程序等功能。

3.2 Lab Windows/CVI实现垂直冲击试验机参数设计计算

垂直冲击试验机测试参数的计算软件界面如图5所示。

在界面的中部有两个图形输出框，其功能分别为显示计算出的加速度波形和垂直冲击试验机工作过程中对地面的冲击力图形，从显示的图形中可以直接判断计算结果是否满足要求。在输入参数一栏中，需要输入工作台和试件质量、底座质量、阻尼器个数等试验机设计参数，以及欲实现的冲击波形脉宽和峰值加速度等基本试验参数。其中，此软件还提供了各种不同的气囊型号进行选择，在气囊不满足受力情况时，软件会自动停止计算，并弹出警告信息。软件输出的不仅仅是冲击波形图和地基受力图，还会输出台面跌落高度，波形发生器刚度以及橡胶的硬度等参数。

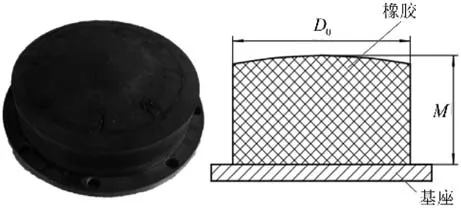
图3 波形发生器示意图

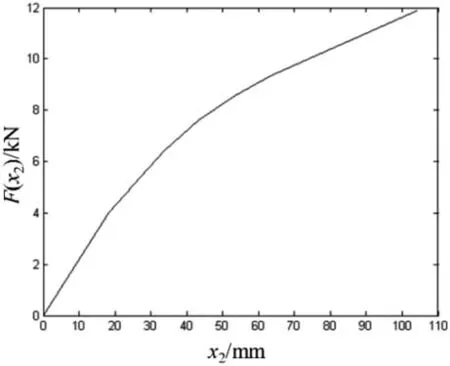
图4 气囊弹性曲线图

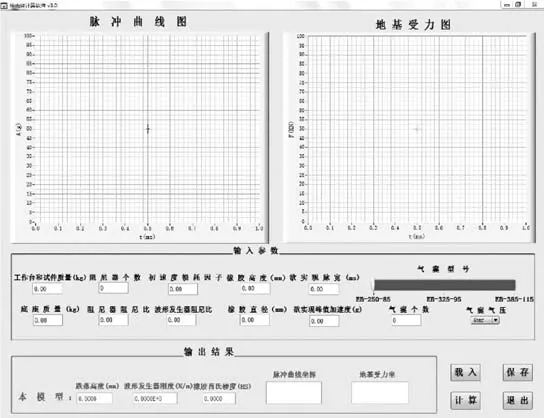
图5 软件界面图

图6 SY11-100垂直冲击试验机图

软件通过龙格库塔法解得的冲击波形和地基承受载荷的数值解最终依靠绘图命令输出，并将数据保存至指定文件夹。

3.3 试验结果的比对

如图6所示，本次试验使用苏州东菱振动试验仪器有限公司生产的型号为SY11-100的气动式垂直冲击试验机。该试验机底座装有4个气囊和8个阻尼器。其中，工作台面是由铝合金铸造而成，其密度为2 700 kg/m3，质量m1=513 kg。底座质量m2=2 500 kg。

本次实验通过产生两个半正弦波形以对比此软件计算的准确性。第一组实验指标为峰值加速度A1=100 g，脉宽D1=6 ms。第二组实验指标为峰值加速度A2=50 g，脉宽D2=11 ms。选取的波形发生器直径和厚度分别为150 mm和15 mm，设其阻尼比c1=0.15。阻尼器的阻尼比c2=0.3。

通过垂直冲击试验机参数计算软件得出跌落高度、波形发生器参数，两次计算结果如图7所示。第一组实验计算出的跌落高度H1=465.58 mm，波形发生器刚度为k1=1.091 5×108N/m，橡胶肖氏硬度HS1=87.30，地基所受最大冲击力F1=15.26 kN。第二组实验计算出的跌落高度H2=342.73 mm，波形发生器刚度为k2=3.511×107N/m，橡胶肖氏硬度HS2=53.93，地基所受最大冲击力F2=15.04 kN。

两组实验实际测得的信号进行滤波后，冲击波形如图8所示。

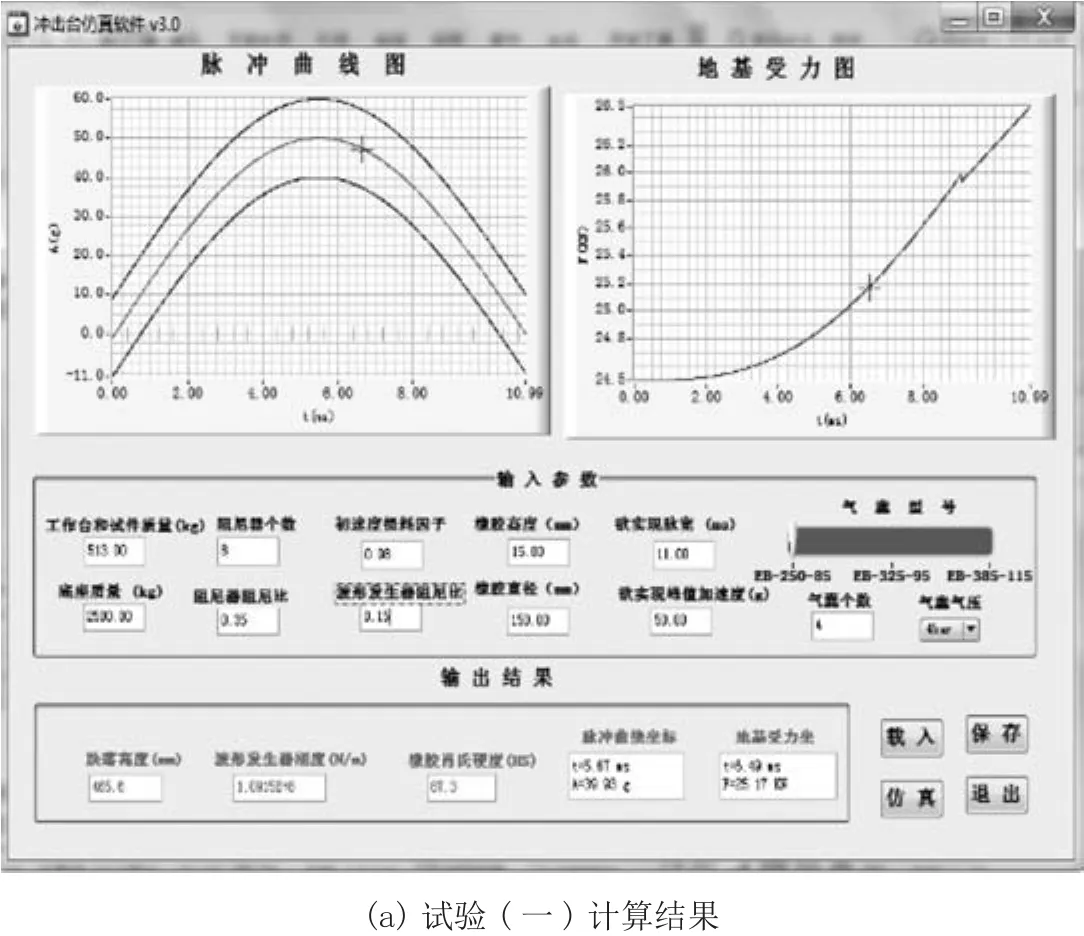
图7 软件计算结果图

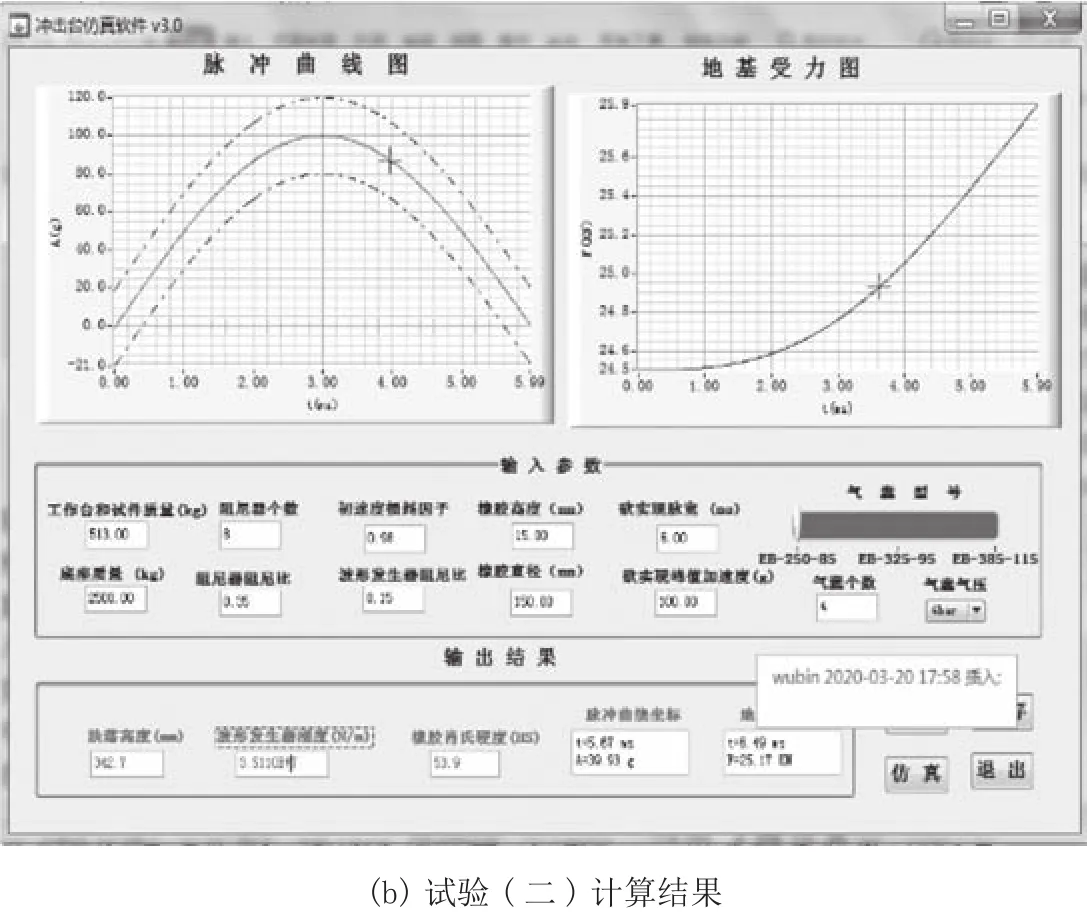
图7 软件计算结果图

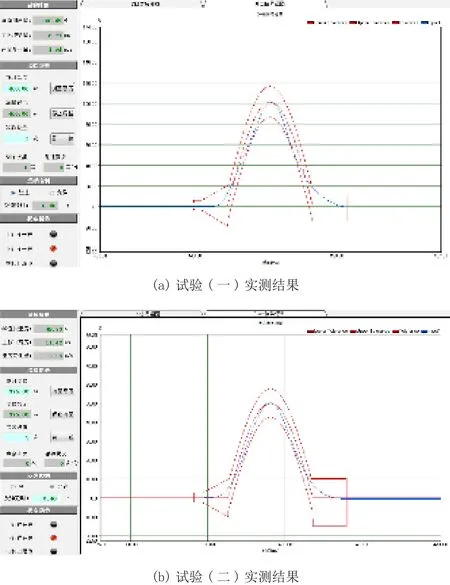
图8 实验结果图

由图8可见，第一组试验垂直冲击试验机实际跌落高度H01=460 mm，产生的半正弦波形峰值加速度A01=100.49 g，脉宽D01=6.77 ms，测得橡胶硬度HS01=85.5。第二组试验垂直冲击试验机实际跌落高度H02=375 mm，产生的半正弦波形峰值加速度A02=49.73 g，脉宽D02=11.42 ms，测得橡胶硬度HS02=55.6。

将软件计算参数与实际试验参数进行比对，如表1所示。可以发现，软件计算的结果精度较高，对垂直冲击试验机设计参数选择具有较好的指导意义。

4 结论

1）考虑了气囊和阻尼器的缓冲作用，建立了垂直冲击试验机的二自由度动力学模型，并将气囊的实际承力和位移曲线作为非线性变量加入动力学方程中，大大提高了冲击波形参数计算的准确性。

2）在保证一定误差的情况下，通过四阶龙格库塔方法求解二阶微分方程组，选取垂直冲击试验机一阶模型的参数作为初始变量，利用二分法重复迭代，保证了二阶微分方程的快速收敛性。

3）采用Lab Windows/CVI开发平台开发了垂直冲击试验机参数计算软件，通过人机交互界面，可以方便计算垂直冲击试验机在实现规定冲击波形时需要提升的高度、波形发生器的厚度和硬度等参数，对指导试验机设计有很好的应用价值。

4）进行了两组对比性试验，结果表明，软件计算结果和试验结果误差较小，可以满足实际的使用需求。

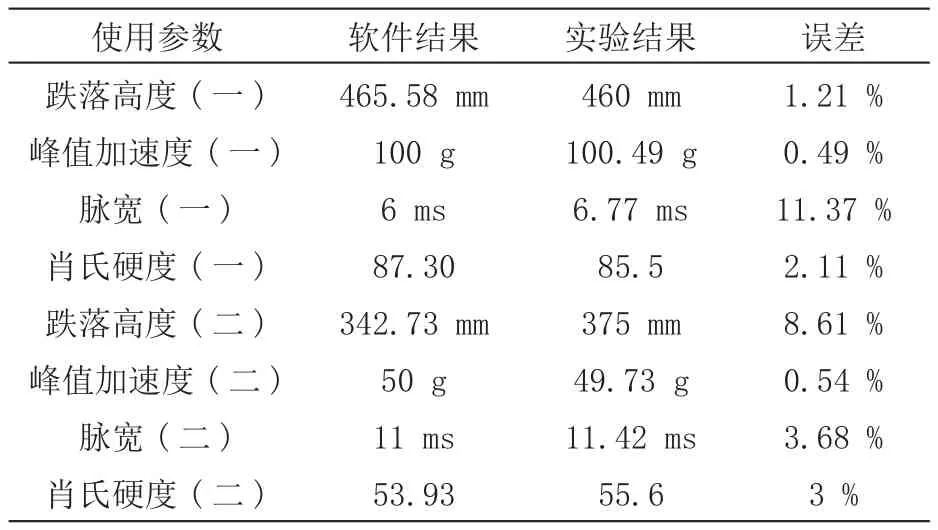
表1 软件计算结果和试验误差