相互作用势对原子核α团簇结构的影响

狄宣平 方德清 何万兵 马余刚

1（中国科学院上海应用物理研究所 上海201800）

2（中国科学院大学 北京100049）

3（复旦大学现代物理研究所教育部核物理与离子束应用重点实验室 上海200433）

结团现象在自然界中普遍存在，原子核内的团簇结构一直都是原子核物理的重要研究方向之一。自从12C 的Hoyle 态的重要性［1-2］被发现后，人们对α团簇结构的研究逐渐升温。稳定的团簇结构一般存在于轻核激发态以及远离β 稳定线的轻核基态中。在α共轭核［3］内，α粒子之间可以形成不同的几何构型，比如12C 中存在三角形或链状的3-α 奇异结构，16O存在正四面体、链状、风筝型或矩形的4-α奇异结构［4-5］，甚至当质量数（A）为28～52 的原子核具有足够高的角动量时环形构型［6-10］也可能存在。为了观测α团簇的不同构型，何万兵等［4-5，11］研究发现，不同构型的α 团簇结构具有不同的巨偶极共振特征峰，并提出可以作为探测α 团簇结构的探针。目前，已经有多种对α 团簇性质的研究方法，但原子核内核子结团的的详细机制还有待进一步研究。

团簇态可以解释为晶体与液相之间的一种混合状态，当温度降低和密度增加时，通过短程力相互作用的粒子系统经历从经典气态到液态再到固态的转变［12-15］。随着密度的增加，系统内粒子的波函数发生重叠，从而形成团簇［16］。团簇的形成受很多因素的影响，比如粒子系统内密度的增加、温度的降低、原子核的形变［16-21］等。Ebran［22］和Freer［23］等从理论上发现核势深度的不同也会影响团簇的形成，Ebran分别用非相对论性密度泛函理论Skyrme SLy4［24-25］和相对论性密度泛函理论DD-ME2［26］计算了20Ne的自洽基态密度，并且DD-ME2 的自洽平均场势要比SLy4深得多，他发现更深的核势更容易产生团簇结构。本文将用输运理论模型研究不同深度的核相互作用势对α 共轭核内团簇结构的产生及其构型的影响。

轻核的团簇结构对原子核中的玻色-爱因斯坦凝聚、低密度核物质状态方程及核天体物理中元素合成过程具有重要意义［1，27-28］。研究不同的核势深度对α 团簇结构的影响，有利于我们了解团簇的形成条件，甚至将来我们可以根据实验数据来探索原子核内的短程力相互作用，从而加深对核物质状态方程的认识。

1 模型和参数调整

量子分子动力学（Quantum Molecular Dynamics，QMD）模型是研究核反应动力学的有效工具，传统的QMD 模型［29］对于中重核描述比较准确，但是对于轻核尤其是远离稳定线的原子核性质描述不太恰当。1996 年Maruyama 等［30-31］通过引入摩擦冷却方法、可变的波包宽度、泡利势等提出了一种扩展的QMD 模型，称为EQMD 模型。该模型能够很好地描述原子核基态性质，特别是轻核的团簇结构。

1.1 EQMD模型介绍

EQMD模型对单个核子的描述采用复数的高斯波包的形式：

式中：Ri和Pi分别表示第i个波包的位置和动量的中心，整个系统的波函数用所有核子波函数的直积来表示。νi表示波包宽度，复数表达式为：

式中：λi和δi分别表示波包的实部和虚部，分别对应核子的坐标和动量分布宽度。

在坐标空间中核子的密度分布函数为：

系统的哈密顿量表示为：

式中：Tc.m.和Hint分别表示系统的零点质心动能和相互作用势能。

EQMD模型选取团簇的判断机制如下：

以上就是判断两个编号为i、j 的核子是否在一个团簇内的公式，这里的参数取值分别是a = 1.7fm和b = 4fm2。

系统的运动方程通过系统拉格朗日量的时间变分得出，其中单核子的正则演化方程可以表示为：

为了准确地描述系统的基态，需要对相空间进行摩擦冷却，这种初始化冷却过程是通过在正则演化方程里加入阻尼项来实现的。加入阻尼项的演化方程可以表示为：

式中：μR、μP、μλ和μδ为阻尼系数，加入阻尼系数后可以使系统冷却到更低的能量状态。

系统的有效相互作用由4部分构成：

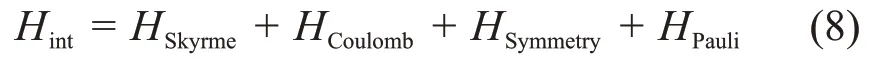
其中Skyrme势使用如下形式：

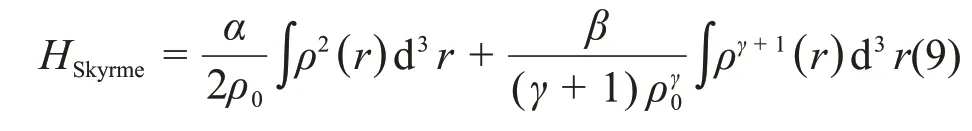
在实际的计算中，不考虑核子的自相互作用，因此式（9）可以化简为：

式中：α =- 124.3MeV，β = 70.5MeV，对应的系统不可压缩系数K∞= 378 MeV。在演化过程中，EQMD系统需要很高精度的数值求解，因此这里的密度依赖项必须严格采用γ = 2的三层嵌套循环来求解。

对称能势具有如下形式：

式中：ρP和ρn分别表示质子和中子的密度，Cs=25 MeV。

泡利势采用如下简单的形式：

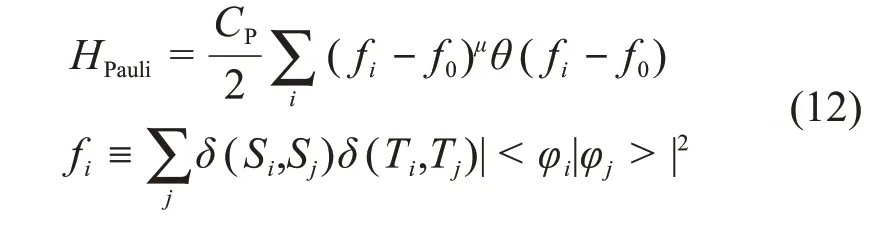
式中：fi为第i 个核子与其他核子的波包重叠函数，位垒参数f0取值为1，CP= 15MeV 为强度参数，μ =1.3。

1.2 泡利势参数调整

目前，EQMD 模型所使用的参数是保持了传统QMD 模型里Skyrme 势的标准形式和参数，并通过调整泡利势参数来符合不同质量区原子核的结合能及均方根半径得到的。虽然在轻核区和重核区模型的计算结果符合得较好，但是在计算中等质量的原子核时，EQMD 模型所得到的原子核平均结合能与实验值差别较大。因此在本工作中，我们首先进一步调整泡利势参数，令CP= 20 MeV，μ = 1.9，使得EQMD模型所得到的平均结合能和均方根半径分别更好地符合实验值［32-33］和经验公式［34］的计算结果。

图1是泡利势参数调整前后EQMD模型中不同原子核的每核子结合能大小和均方根半径大小。其中方块是泡利势参数调整之前EQMD 模型的计算结果，圆形是泡利势参数调整后EQMD模型的计算结果［32-33］，三角在图1（a）、（b）中分别代表实验值和经验公式计算的结果［34］。从图1 可以看出，调整了泡利势参数之后的EQMD 模型所得到的结果比调整之前更好，特别是结合能的结果，因此在接下来的计算和对比中我们将采用调整后的势参数。

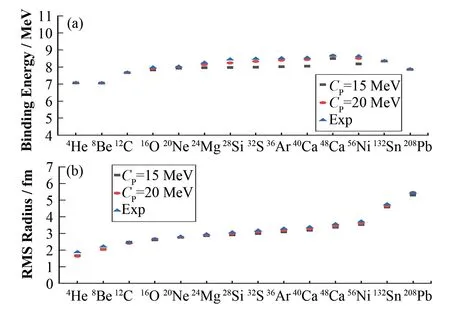
图1 泡利势参数调整前后EQMD模型中不同原子核的每核子结合能(a)和均方根半径(b)Fig.1 Binding energy of each nucleon(a)and RMS radius of different nuclei(b)in the EQMD model before and after adjustment of Pauli potential parameters

1.3 Skyrme势参数调整

本文的目的主要是研究不同深度的核势对α团簇结构的影响，为了得到不同深度的核势，我们调节了Skyrme势参数［35-41］，具体步骤如下：

首先，Skyrme势参数应满足无限大对称核物质在饱和密度处的各项基本特性（e∞=- 16 MeV，ρ0=0.165fm-3，P = 0）；其次，考虑不对称核物质（加入对称能，考虑有效质量）；然后，引入新的约束力（加入泡利势，考虑泡利不相容原理）；最后，考虑有限核基本性质，调节泡利势参数，使其输出的原子核（16O，40，48Ca，56Ni，132Sn，208Pb）的结合能和均方根半径符合已知实验值。

在零温度下，对于无限大均匀的核物质且不考虑库仑相互作用时，系统的能量密度可以简写为：

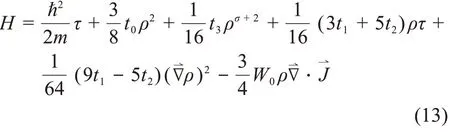
式（13）右边第一项是动能项，第二、第三项分别是吸引项（两体项）和排斥项（密度相关项），后面分别是动量相关项、表面能项以及自旋轨道耦合项。EQMD 模型里的Skyrme 相互作用只考虑了两体项和三体项，通过对比式（9）中的两体项和三体项可以得出：

其中：Θs= 3t1+ 5t2，当系统内核子密度等于无限大均匀核物质的饱和密度时，式（14）的平均结合能应为-16 MeV，式（15）的压强应为0。从式（14）、（15）可以看出，无限大均匀核物质的平均结合能和压强只与两体项，密度相关项和动量相关项有关，由于EQMD 模型必须严格执行γ = 2 的三层循环，因此σ = 1 是确定的，为了得到不同的核势，我们在EQMD模型里引入动量相关项。

这里我们直接引入QMD 模型里的动量相关项［28，42-46］：

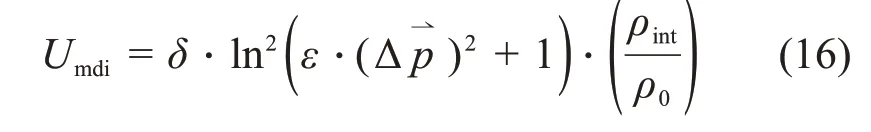
引入了动量相关项后，核子在运动方程里的有效 质 量 为m∗/m= 0.75，式（16）中 的 参 数δ =1.57 MeV，ε = 500。依据Skyrme 势参数的调节步骤，我们可以计算得出这时的α =- 134.6 MeV、β =62.2 MeV，此时系统的不可压缩系数为K∞=404 MeV。同时，为了使EQMD 模型所得到的平均结合能和均方根半径分别更好地符合实验值和经验公式的计算结果，调整泡利势参数为：CP= 28 MeV，μ = 1.3。

图2是引入动量相关项前后EQMD模型中不同原子核的每核子结合能大小和均方根半径大小。其中方块是没加动量相关势的EQMD 模型的计算结果，圆形是加入动量相关势的EQMD模型的计算结果，三角在图2（a）、（b）中分别代表结合能的实验值［32-33］和经验公式计算的均方根半径［34］。从图2可以看出，EQMD 模型加入动量相关项前后所得到的平均结合能和均方根半径都比较符合实验值和经验公式的计算结果，说明EQMD模型加入动量相关项前后对原子核基态的描述均具有可靠性。

图2 引入动量相关项前后EQMD模型中不同原子核的每核子结合能(a)和均方根半径(b)Fig.2 Binding energy of each nucleon(a)and RMS radius of different nuclei(b)in the EQMD model before and after adding the MDI

2 结果和讨论

我们运用动量相关项加入前后两组不同的参数对4≤A≤40的α共轭核基态进行模拟计算，发现这两组参数所计算出的原子核的每核子核势深度确实不同。图3描述的是加入动量相关项前后EQMD模型所计算的每核子核势深度的大小，其中方块是未加动量相关项的EQMD模型的计算结果，圆形是加入动量相关项后模型的计算结果。如图3 所示，加入动量相关项后EQMD 模型计算得出的核势深度比没加动量相关项时计算得出的核势深度要深。

图3 不同α共轭核的每核子核势深度Fig.3 Depth of Skyrme potential of each nucleon of different α conjugated nuclei

在EQMD 模型中，通过演化后，每个原子核形成α 团簇的数目是不固定的。图4 是加入动量相关项前后EQMD 模型所计算的4≤A≤40 的α 共轭核内的核子全部形成α团簇的概率。图中方块是未加动量相关项时模型的计算结果，圆形是加入动量相关项后模型的计算结果，纵轴里n=A/4。从图4 可以看出，加入动量相关项后，全部由α团簇结构构成的原子核的出现概率明显升高。由于加入动量相关势后核相互作用势的深度增加，也可以说核势深度的增加有助于α 团簇结构的出现，这个结果符合Ebran［21］和Freer［22］等理论研究的结论。

图4 不同α共轭核内的核子全部形成α团簇结构的概率Fig.4 The probability of all nucleons in different α conjugated nuclei forming α cluster structure

在用EQMD 模型模拟12C 和16O 的原子核基态时，我们发现核势深度的增加不仅有助于α 团簇结构的出现，而且对α团簇的构型也有一定影响。图5是由α 团簇构成的12C 和16O 的不同构型所占的比例。图中方块是没加动量相关项的EQMD 模型的计算结果，圆形是加入动量相关项后EQMD模型的计算结果。由图5可知，加入动量相关项后，也就是核势深度加深后12C 中链状结构减少，三角结构增多；16O 中链状结构和矩形结构减少，风筝型结构和四面体结构数目增多。因此我们可以初步得出结论：核势深度的增加使得α 团簇结构由分散的构型向更紧凑的构型转变，原子核内的α 粒子趋于集中分布。

在研究过程中我们发现，在EQMD模型中加入式（16）形式的动量相关项虽然可以为原子核的初始化过程提供更深的核势深度，但并不利于原子核在自由演化时的稳定性，约有5%的轻核会在自由演化中坍缩或发散掉，随着核子数目的增多，坍缩或发散掉的原子核数目也会增多。

3 结语

图5 由α团簇构成的12C(a)和16O(b)的不同构型所占的比例Fig.5 Proportion of different configurations of 12C(a)and 16O(b)consisting of α clusters

通过上面的研究分析可以看出，调节了泡利势参数后EQMD 模型对原子核基态性质的模拟更可靠。对于EQMD模型来说，加入动量相关项会导致原子核在自由演化过程中的稳定性降低。核势深度的增加，有利于α 共轭核内的核子全部组成α 粒子，同时也会导致这些α粒子的构型发生变化。这为深入研究核物质状态方程对原子核基态和结团现象的影响具有参考价值。目前，我们对核力的本质及原子核结构的认识还有限，需要采用更多的研究方法和技术进行深入研究。随着深度学习及量子计算等［47-48］新的方法与技术在核物理领域的应用，未来人们对原子核性质的认识将会更加深入和全面。