不同着角下爆炸成形弹丸对坦克发动机等效靶的毁伤效应

柯源， 刘彦， 黄风雷

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

爆炸成形弹丸(explosively formed projectile, EFP)是一定形状的药型罩被爆炸载荷压垮、翻转，闭合形成一个高速杵体弹丸[1]，聚能战斗部已广泛应用于末敏弹等远距离反装甲武器系统中. 末敏弹可以通过攻击坦克的顶部装甲方式对坦克发动机造成毁伤，而近年来国内外对坦克发动机的毁伤研究鲜有报道，因此开展EFP对坦克发动机的毁伤效应研究具有重要意义.

目前，国内外对于坦克的毁伤研究在实验研究、理论分析、数值模拟等方面取得了一定进展，聂源等[2]为揭示三明治结构爆炸反应装甲(ERA)对爆炸成形弹丸侵彻效应的影响，开展了铜质杆式EFP对披挂典型斜置角ERA主靶板的侵彻效应实验. 并获得了EFP对主靶板的剩余侵彻深度(RDOP). 曹兵[3]等分析了EFP对有限厚45#碳钢靶和有限厚603靶板的侵彻规律，获得了45#碳钢板与603靶板的等效关系. 杨莉等[4]对用于反舰(潜)复合式鱼雷战斗部的前级聚能装药爆炸成形弹丸进行了成型实验及其对多层含水复合装甲的侵彻实验，得到了爆炸成形弹丸的飞行特性和对含水复合装甲的侵彻规律. 樊菲等[5]利用LS-DYNA仿真软件，对爆炸成形弹丸毁伤能力与EFP侵彻着角关系进行了研究. Ricardo等[6]利用Lagrange法研究LS-DYNA软件在简易爆炸成形弹丸在侵彻中的适用性，通过大量的现场实验验证了不同结构参数EFP对不同摆放角度钢靶的数值仿真结果.

国内外关于EFP对坦克毁伤研究主要集中在装甲防护上，而对坦克车体内部发动机的毁伤研究较少，缺乏相应的毁伤数据， EFP从坦克顶部攻击坦克发动机，不仅会对坦克的装甲防护造成毁伤，而且当EFP依靠动能击穿装甲进入车体内部后会对发动机形成毁伤，EFP穿靶过程涉及靶后破片的二次毁伤作用，是一个十分复杂的过程，由于缺乏相关的实验，因此开展爆炸成形弹丸对坦克发动机等效靶的毁伤效应研究刻不容缓.

本文对典型主战坦克发动机进行了结构等效，开展了不同着角下EFP对发动机等效靶的毁伤实验，获得了发动机等效靶的破孔尺寸以及毁伤面积，并结合仿真软件对EFP在不同着角下侵彻装甲防护层进行了研究，研究结果为反坦克战斗部的设计和坦克发动机的防护奠定了基础.

1 等效靶设计

本文选取某主战坦克发动机为研究对象，发动机的外廓尺寸为1 466 mm×896 mm×909 mm. 发动机的框架主要是由上下曲轴箱组成的壳体，上下曲轴箱材料均为ZL104. 在进行毁伤效应实验时，将坦克发动机上下曲轴箱组成的主体，等效成长宽高均为原轮廓尺寸1/2的箱体作为发动机等效靶，如图1所示，等效靶内部由铝型材组成的框架支撑，各面与支撑框使用螺栓连接，防护板也通过螺栓固定在框架上，其尺寸如表1所示.

图1 发动机等效靶Fig.1 Engine equivalent target

表1 箱体各面厚度以及尺寸Tab.1 Thickness and size of all sides of the box

设计如图2所示的发动机等效靶支架，通过调整支架短臂实现EFP的不同着角侵彻. 根据材料强度等效原则，选取45号钢作为顶部装甲等效靶材料，2A12铝作为发动机等效靶材料，等效关系如式(1)所示[7].

(1)

式中：σbi为被替代材料的强度极限；σbci为率合金的强度极限；ρi为被替代材料的密度；ρbci为铝合金密度；h为原材料厚度；hc为等效材料厚度.

2 实验及结果分析

2.1 实验装药

装药口径D为104 mm的聚能装药，由药型罩、主装药、传爆药和壳体组成，其中药型罩为球缺形药型罩，球缺形部分内径为135 mm，外径为142 mm，药型罩的最大厚度为6 mm，装药为船尾形装药，直径和高度分别为104 mm和78.5 mm，装药为压装的奥克托儿，密度为1.821 g/cm3，壳体材料为30CrMnSi，壳体厚度4 mm.

2.2 实验装置及测试布置

实验布置如图3所示，装药与测速靶相隔1 m，在靶前布置用于测量EFP初速的金属丝网靶，两网靶间隔0.5 m，测速靶与钢靶迎弹面中心距离0.5 m，此外布设高速摄影用于观察EFP侵彻靶板的过程. 实验时靶板设置(相对水平面成α角)0°、30°、45°、60°角度下的工况，每种工况需要对靶架进行调整，经过角度换算EFP的着角与α相等.

图3 实验布置示9意图Fig.3 Setup of the experiment

2.3 实验结果与分析

静爆毁伤实验一共4发，第1发实验α=0°，测得的EFP速度为1 712 m/s，钢靶被完全贯穿并形成直径为64 mm的弹孔，铝箱顶面出现瓣裂形成尺寸约为109 mm的破孔，毁伤面积达到93.3 cm2,与顶面相对的底面则出现了许多大小不一的破孔，毁伤面积达到297.2 cm2，而且整个铝板分裂成两块，因为EFP在穿过钢靶和发动机顶面后会产生许多不规则的靶后破片，在破片和残余弹体的联合作用下，底面便形成了这种毁伤效果. 在这种工况下EFP飞行轨迹与靶板垂直，因此铝箱除顶面和底面外的其他部分并没有明显的毁伤情况.

图4 着角0°发动机等效靶毁伤情况Fig.4 Engine equivalent target damage at 0°

第2发实验α=30°，测得的EFP速度为1 625 m/s，钢靶被完全贯穿并在钢靶正面形成直径为95 mm的弹孔，位于钢靶后的铝箱顶面出现瓣裂形成直径为130 mm的破孔，毁伤面积达到132.7 cm2,底面的上半部分形成4个明显的破孔，从左到右尺寸依次为50 mm×10 mm，60 mm×60 mm，80 mm×50 mm，83 mm×49 mm，毁伤面积达到85.7 cm2，有些破片未击穿底面留下若干鼓包，与第1发从铝靶底面飞出不同的是EFP残余弹体从铝箱侧面穿孔飞出，在侧面留下尺寸为47 mm×26 mm的孔洞，毁伤面积为12.2 cm2.

图5 着角30°发动机等效靶毁伤情况Fig.5 Engine equivalent target damage at 30°

第3发实验α=45°，测得的EFP速度为1 611 m/s，钢靶被完全贯穿并且形成尺寸为105 mm×87 mm的椭圆形弹孔，位于钢靶后的铝箱顶面出现瓣裂形成尺寸为260 mm×97 mm的不规则破孔，毁伤面积达到410.8 cm2，底面则出现了2个破孔，大孔尺寸为69 mm×36 mm，小孔尺寸约为25 mm×25 mm，毁伤面积达到31.1 cm2，铝箱侧面留下尺寸为11 mm×16 mm的孔洞，面积为1.8 cm2.

图6 着角45°发动机等效靶毁伤情况Fig.6 Engine equivalent target damage at 45°

第4发实验α=60°，测得的EFP速度为1 684 m/s，钢靶未被贯穿，钢靶正面弹坑尺寸约为85 mm×113 mm，背面形成隆起的鼓包，铝箱无毁伤. EFP在不同着角下对钢靶的毁伤情况见表2.

图7 着角60°发动机等效靶毁伤情况Fig.7 Engine equivalent target damage at 60°

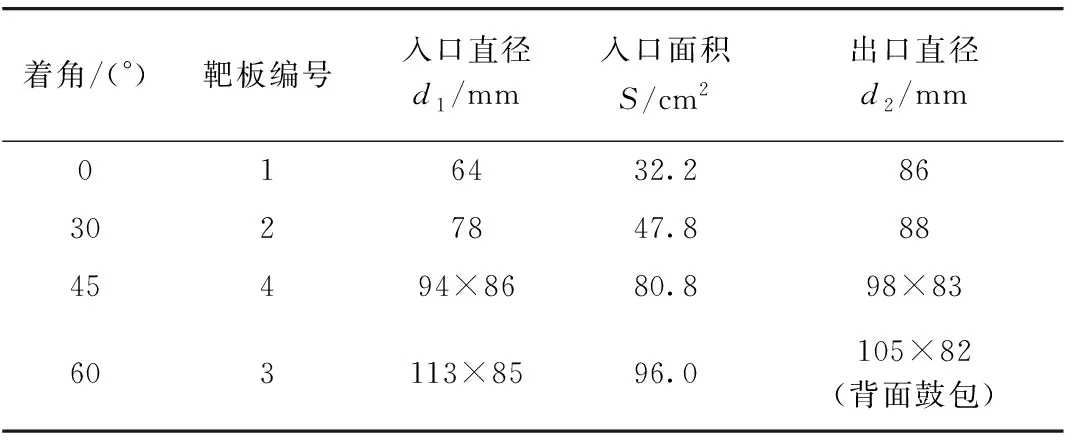
表2 钢靶EFP斜侵彻实验数据记录Tab.2 Steel target test data

从4发实验的结果来看，只要EFP能够穿透钢靶均能对铝靶造成不同程度的毁伤，随着着角从0°增大到45°钢靶入口面积增加了198%，铝箱顶面破孔面积增加了172%，铝箱底面的破孔数量以及破坏范围呈现逐渐减小的趋势，可以预测对发动机内部结构毁伤的范围也随之减少，同时由于着角增大EFP会对侧面形成毁伤，4发实验中着角30°和45°情况下对侧面形成毁伤，侧面毁伤的面积随着着角增大急剧减少了86%.

3 数值模拟

3.1 计算模型的建立

根据实验结果可知，EFP能否穿透钢靶对于发动机的毁伤至关重要，本文采用LS-DYNA有限元软件对0°、10°、20°、30°、40°、45°、50°、55°、57°、60°着角下EFP侵彻钢靶的过程进行数值模拟，炸药与靶板的距离为500 mm，计算模型如图8所示. 模型采用1/2模型进行简化计算. 装药起爆点位于炸药顶部中心，采用Lagrange算法，单位制为cm-g-μs. 在模型的对称表面加入对称边界条件，药型罩与炸药采用滑移接触，药型罩和靶板，炸药和壳体都采用侵蚀接触，炸药在30 μs时删除.

图8 聚能装药与靶板有限元计算模型Fig.8 FE models of shaped charge and target

3.2 材料模型及参数

炸药为Octol炸药，采用High-Explosive-Burn材料模型和JWL状态方程，具体参数如表3所示.

表3 炸药材料参数Tab.3 Explosive material parameters

由于EFP成型和侵彻过程属于大变形、高压和高应变率问题，对于药型罩和壳体采用Johnson-Cook塑性本构模型，靶板采用Plastic-Kinematic本构模型，具体参数如表4和表5所示.

表4 紫铜和壳体材料参数Tab.4 Copper material parameters

表5 钢靶材料参数Tab.5 Steel target material parameters

3.3 数值模拟结果

表6为钢靶入口最大破坏尺寸实验值与仿真值对比，从表中可以看出4种工况下仿真值与实验值的误差均小于8%，仿真得到EFP速度为1 550 m/s与实验结果的平均值1 658 m/s的误差为6%，说明通过LS-DYNA软件得到的仿真结果具有较高准确性. 表7为实验破孔形貌与仿真结果的对照，当EFP以不同着角侵彻靶板时，靶板正面的破孔形状及大小均与着角有关，随着角增大，入口最大破坏尺寸越大，且破孔形状越不规整. 着角0°时孔洞形状接近标准圆形，随着角的增大，孔洞形状由圆形逐渐向椭圆形过渡. 当着角从0°增加到30°时，靶板正面入口最大破坏尺寸变化不大，比着角0°增大了19.7%，当着角增大到45°时，最大破坏尺寸比着角0°增大了38%，增长量约为着角30°时的2倍，这是由于当着角较大时，EFP沿靶板对称轴方向分速度较大，侵彻路程变长，在靶板上留下更大的孔径. 入口最大破坏尺寸随着角的变化关系亦可从图9看出，即入口最大破坏尺寸随着角增大呈上升趋势，随着着角增大最大入口尺寸上升的趋势越来越快，特别是着角大于45°的情况下，增长速率明显增大. 图10为EFP出靶动能随着角变化的曲线，EFP穿靶的剩余动能随着角增大呈下降趋势，着角在10°～40°之间剩余动能下降幅度最大，之后下降趋势趋于平缓.

表6 钢靶入口最大破坏尺寸实验值与仿真值对比Tab.6 Comparison of experiment and simulation of maximum destruction size of steel target entrance

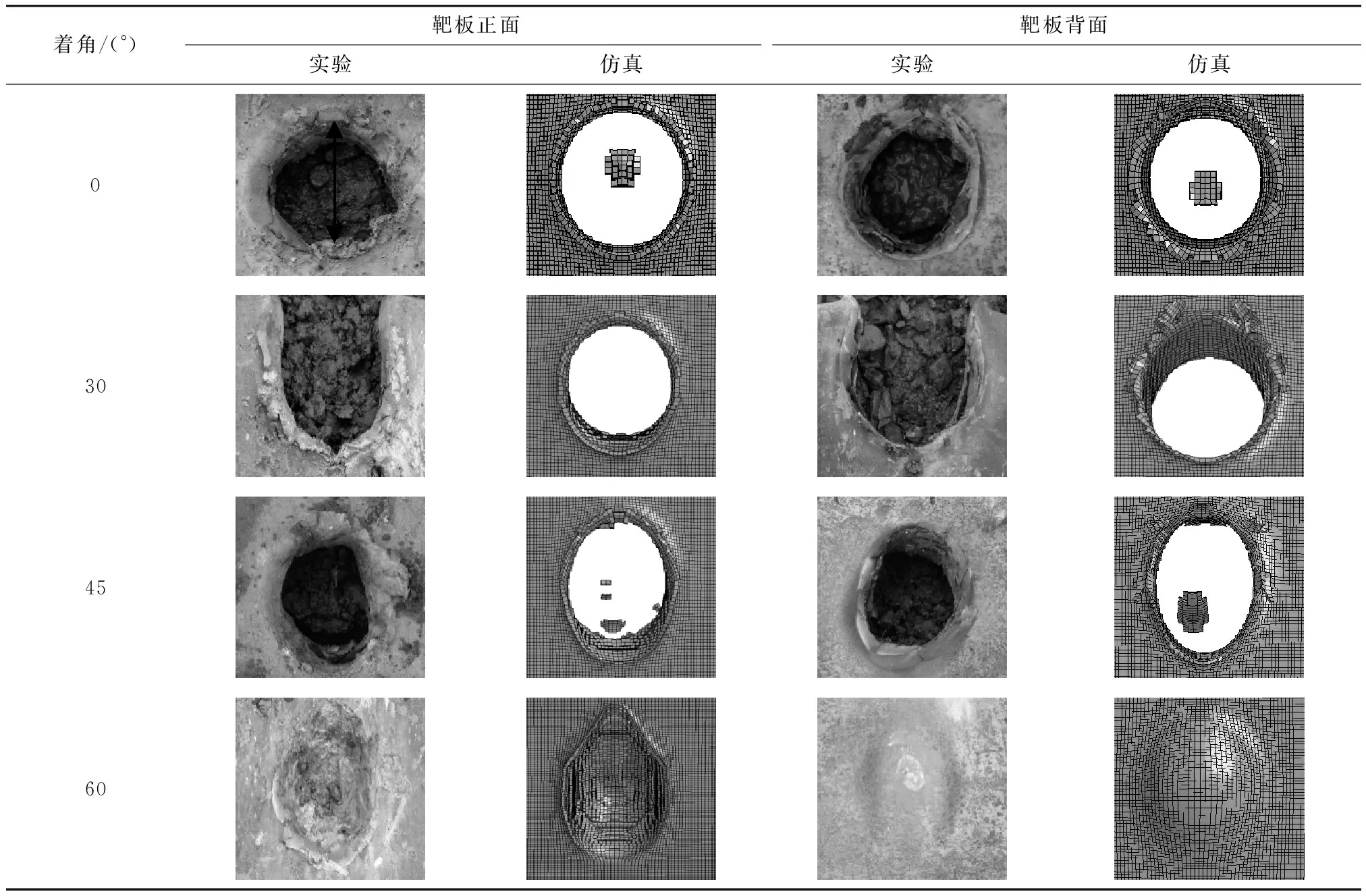
表7 钢靶实验破孔结果与仿真结果对照Tab.7 Corrosion results of steel target experiments and simulation results

图9 EFP钢靶最大入口尺寸与EFP着角的关系曲线Fig.9 Curve of the maximum inlet size of EFP steel target

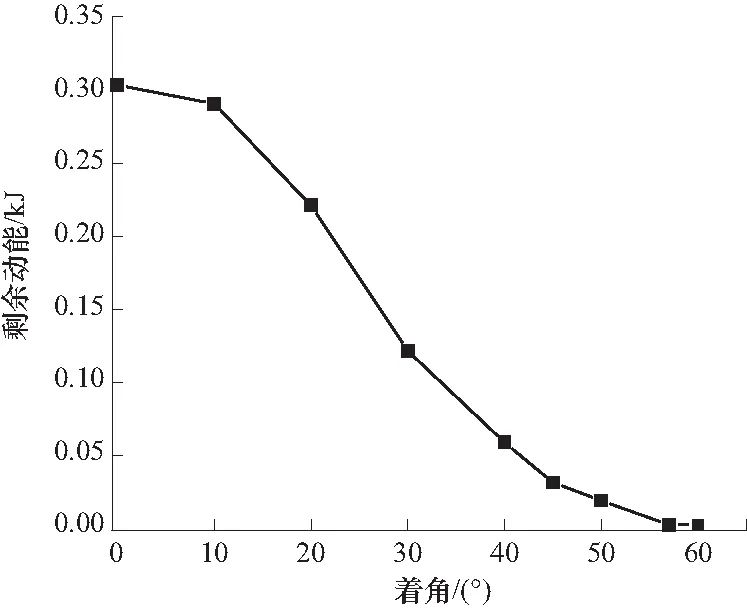
图10 EFP剩余动能与EFP着角的关系曲线Fig.10 EFP target kinetic energy and EFP penetration angle penetration angle

结合实验以及仿真可以发现在着角55°～60°存在一个临界角度，对这个范围每隔1°进行分析，仿真中出现临界着角57°，此时EFP剩余动能降为0，靶板即将被穿透. 通过这一临界值，可以做出如下判断：EFP着角α<57°时，钢靶均被贯穿，并且随着角的增大，钢靶最大破坏尺寸越来越大，毁伤的面积也相应升高，弹丸对钢靶后的铝箱毁伤效能减弱. 出现这种现象的原因是，弹丸以一定的速度撞击钢靶时，由于弹丸着角的增加，弹丸着靶部分面积增大，弹丸与靶板相互作用的部分增大，而且贯穿靶板的厚度变大，弹丸贯穿钢靶后的动能损失上升，因此贯穿钢靶后的弹丸在与铝箱的作用过程中具有更小的动能，毁伤能力也更弱；当着角α≥57°时，EFP无法贯穿钢靶，对铝箱并无毁伤.

4 结 论

针对不同着角下EFP对坦克发动机等效靶毁伤进行了实验，并对实验结果进行了分析对比和数值模拟，得到如下结论：

① 当EFP能够贯穿钢靶的情况下均能对铝靶进行毁伤，随着着角的增大，钢靶穿孔和铝箱顶面破孔面积显著增大，EFP侵彻钢靶过程损耗的动能增大，EFP对发动机的毁伤程度呈减小趋势；

②从仿真结果来看，Lagrange算法在不同着角下EFP侵彻钢靶的模拟中，EFP速度和钢靶入口的最大破坏尺寸与实验结果基本一致，因此后续按照该方法计算的结果具有较高的可信度；

③随着着角增大，EFP侵彻路径变长，着靶面积增加，钢靶最大入口尺寸呈上升趋势， EFP穿靶的剩余动能呈下降趋势，此外还得到的EFP穿靶的临界角57°，当EFP着角α≥57°无法贯穿钢靶，对铝箱并无毁伤.