卫星编队的管道模型预测控制方法研究

邹恒光， 宋继良， 王军政， 张磊， 史大威

(1.北京理工大学 自动化学院，北京 100081；2.中国空间技术研究院，北京 100094)

近年来，随着全球通信业务的日益增长，单个卫星组成的系统越来越难以满足庞大且多样化的通信需求. 为了解决这一问题，人们的目光开始投向多卫星星座的建设. 相比于单个卫星组成的系统，多卫星组成的星座编队不仅具有强大的覆盖能力，更具有良好的容错性，因而受到国内外研究学者的广泛关注[1-4].

通信卫星多位于地球静止轨道，难以避免会存在轨位有限的问题. 因此，静止轨道往往会将多颗卫星共位放置在同一个或邻近的定点区域内，组成通信卫星星座编队. 为了保证卫星编队内卫星相互之间的安全以及星座工作的稳定性，需要定期地进行构型保持控制，避免其因为空间环境摄动等因素导致星座失效. 杨晓龙等[5]针对Walker-δ星座提出了基于覆盖性能分析的星座构型保持方法，其主要思想是当侦测到某一卫星的覆盖区域异常时，即对其进行保持控制，从而保证星座整体构型不会被破坏. 黄勇等[6]基于卫星相对运动非线性动力学方程和一致性理论分别设计两种自适应控制器，实现了卫星编队飞行的相对位置的协同控制.

模型预测控制作为一项在过程控制领域应用较为广泛的技术，近年来开始逐渐在航天领域崭露头角[7-9]. 吴宝林等[10]利用相对平均轨道根数模型设计了针对卫星编队队形机动控制的模型预测控制器. Weiss等[11]基于CWH模型设计了模型预测控制器，实现了对于具有连续小推力静止轨道卫星的位置保持控制. 然而，文献中多考虑近似模型，存在着模型的不确定性，会对模型预测控制的性能产生影响. 为了克服模型不确定性的影响，可以采用鲁棒模型预测控制的方法. 最为常见的一种鲁棒模型预测控制器是基于管道的模型预测控制器(Tube-MPC)[12-14]. Tube-MPC的主要思想是将系统不确定性刻画成一个管道，即所允许的误差范围，然后设计控制律使得系统的状态轨迹保持在管道内，并向名义状态轨迹收敛.

本文针对静止轨道卫星编队的构型保持问题，提出了基于管道模型预测控制的构型保持策略. 第1部分构建卫星与参考轨道之间的轨道相对动力学模型，并对卫星编队控制问题进行介绍；第2部分介绍了管道模型预测控制器的基本设计方法；第3部分针对4星编队控制进行了仿真验证. 仿真结果表明所提出的控制方法能够很好地实现编队控制要求.

1 卫星编队控制问题描述

1.1 基本轨道动力学模型

图1描述了卫星轨道动力学中常用的2个坐标系，地心惯性(earth-centered inertial, ECI)坐标系和Hill坐标系. ECI坐标系以地球中心为原点，X轴沿某一特定历元的春分点方向，Z轴指向北极点，Y轴组成右手正交坐标系，常见的地心惯性坐标系为J2000坐标系. Hill坐标系以卫星质心为原点，r轴为径向，方向为地心-卫星连线方向向外，t轴为切向，方向沿卫星线速度方向，n轴为法向，组成右手正交坐标系.

图1 航天器轨道常用坐标系示意图Fig. 1 Commonly used coordinates of the satellite orbit

通常情况下，卫星绕地球转动的动力学模型在地心惯性坐标系下可以描述为

(1)

式中：r为卫星的位置矢量，r=|r| 为卫星位置矢量的模，即卫星质心到地心的距离；μE为地球的引力系数；F为控制力矢量；m为卫星质量；ap为空间摄动加速度矢量. 对于静止轨道卫星，其所受到空间摄动[15]通常包含地球非球形引力摄动，日月引力摄动和太阳光压摄动，仿真所考虑而这些摄动力会使得卫星产生漂移，偏离定点位置. 本文在设计控制器实现静止轨道卫星编队构型保持的同时，也考虑了各种空间摄动的影响，并相应的进行补偿.

1.2 轨道相对动力学模型

CWH方程常被用于描述2颗卫星之间的相对运动，而且对于相对运动距离远小于轨道半径的情况，可以利用线性化后的模型来近似，从而便于控制器的分析与设计. 对于参考轨道为圆轨道的卫星，其与参考卫星在Hill坐标下的相对位置可以用CWH方程来描述[16]

(2)

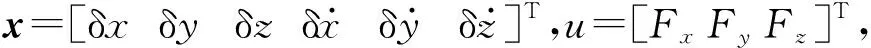
(3)

式中：

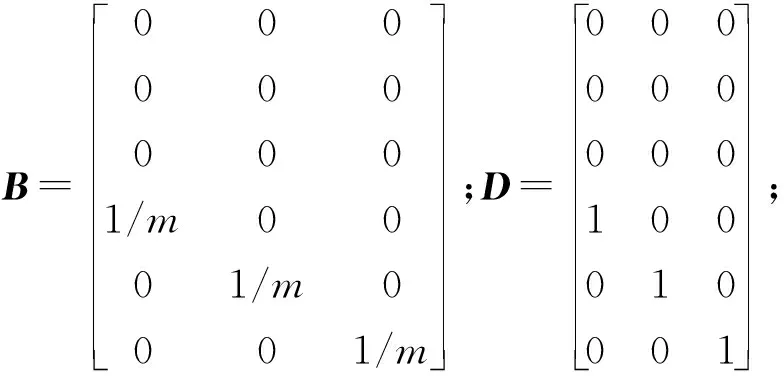
ap(t) 为总的摄动加速度，可由空间摄动力的解析模型计算得到.

通过零阶保持的方法对式(3)进行离散化，可以得到

x(k+1)=Adx(k)+Bdu(k)+Ddap(k)

(4)

1.3 卫星编队控制问题

设某卫星编队有Na颗卫星，考虑主从式编队方式，其中有1颗主星，Na-1 颗从星. 主星参考轨道为一标准圆轨道，除主星外，每颗跟随卫星参考轨道均由其相邻的卫星轨道确定.

由式(4)可知，每颗卫星相对于其参考轨道的动力学方程可以表示为

xi(k+1)=Adxi(k)+Bdui(k)+

Ddai,p(k) ∀i∈{1,2,…,Na}

(5)

模型预测控制算法是基于模型的控制方法，也就是说，模型的精度直接影响最终的控制效果. 然而，由于采用了离散化后的线性模型，而且对摄动力的计算也采用了相应的近似方法，势必会产生模型的误差. 将模型的误差连同各类外部不确定性视为系统的加性不确定性wi∈Wi，那么，卫星实际的相对运动模型可以表示为

xi(k+1)=Adxi(k)+Bdui(k)+

Ddai,p(k)+wi∀i∈{1,2,…,Na}

(6)

同时，系统状态与系统输入也应该满足一定的约束. 就静止轨道卫星而言，一般希望卫星不要偏离定点位置超过一定范围，即对卫星相对参考轨道的位置矢量有着一定的约束. 而且，由于卫星推进器推力有限，故对控制输入也有一定限制. 那么这些约束可以描述为

xi∈Xi=xi∈6:Fxxi≤hx

(7)

ui∈Ui=ui∈3:Fuui≤hu

(8)

那么，考虑到模型不确定wi，卫星编队的控制目标可以简单描述为：

① 所有卫星能够跟踪给定的期望轨道；

② 卫星编队保持一定的构型，且不发生碰撞.

2 管道模型预测控制控制器设计

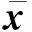
Ddai,p(k) ∀i∈{1,2,…,Na}

(9)

接下来，定义真实卫星相对位置状态与名义状态之间的误差为

(10)

为了使得管道内的真实状态向名义状态靠近，设计以下次级控制器

(11)

那么，由式(6)、式(9)～(11)可以得到对应的误差系统

(12)

式中K为反馈矩阵，且Ad-BdK是Hurwitz的.

对于式(12)所示的误差系统，定义其鲁棒正向不变集为φi,k，即

(13)

那么，在任意时刻k，系统的真实状态满足

(14)

式中 ⊕ 为两个集合间的闵可夫斯基和.

同时，卫星相对位置的名义状态与名义控制输入满足

(15)

(16)

如此以来，只要名义系统的状态和控制量满足式(15)和式(16)，真实系统的状态即满足式(7)和式(8).

接下来，设预测步长为Np，定义代价函数Ji

(17)

对于所有i∈{1,2,…,Na} ，求解下述优化问题

(18)

(19)

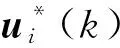
3 仿真结果

如图2所示，本文考虑一种4星编队构型，4颗相同的卫星均为静止轨道卫星. 主星参考信号为标准圆轨道；从星1与主星在同一轨道平面，且从星1的参考轨道由主星生成，二者星下点轨迹相差地理经度0.2°；从星3与从星4与从星2不在同一轨道面，二者参考轨道由从星2生成. 从星3与从星2星下点轨迹地理经度相差0.2° ，地理纬度相差0.05° ，从星4与从星2地理经度相差0.2° ，地理纬度相差 -0.05° . 表1给出了4颗卫星的初始轨道，其中a,e,i,Ω,ω,υ分别表示轨道的半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角和真近点角.

图2 4星编队构型与星间通信拓扑示意图Fig. 2 Structure of the formation of four satellites and its network topology

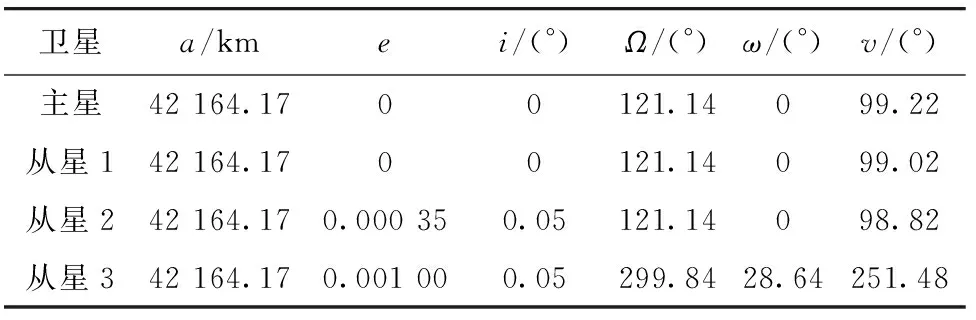
表1 卫星编队初始轨道Tab1 Initial orbits of the satellites formation

基于上节所设计的管道模型预测控制算法，对4星编队的构型保持进行了180 d运行仿真，仿真历元为2019年1月1日00∶00∶00，仿真步长为100 s，控制器离散化步长为3 600 s. 4颗相同的卫星质量均为2 000 kg，卫星面质比为0.005 6，光反射系数为1.2，推进器最大推力为500 mN. 仿真考虑的空间摄动影响因素如表2所示，且由于所仿真的卫星为GEO卫星，大气摄动影响可以忽略. 对于单颗卫星，令各方向相对位置误差最大容许值为±0.01°，即±7 500 m. 模型不确定性设为

wi(k)=[2 000 m2 000 m2 000 m0.5 m/s0.5 m/s0.5 m/s]i∈{1,2,3,4}

表2 空间环境摄动Tab.2 Environmental perturbations in the simulation

如图3所示，180 d的仿真内，主星与各从星星下点轨迹均满足 ±0.01°的约束(虚线部分). 对于从星3与从星4的轨迹在最开始会短暂的超出约束的问题，原因是控制器在最初阶段的响应滞后，且与初始轨道的设计有关. 在仿真的最开始可以将约束放松，以免出现优化问题无解的情况，导致控制器故障. 图4中，各跟随卫星(从星1、2、3)与领导卫星(主星、从星1)之间的相对距离基本保持稳定，最大波动误差不超过4 km. 且相对于编队卫星之间的间距(147 km, 152 km)，4 km的波动误差可以接受. 仿真结果显示，当控制精度限制在±0.01°时，180 d内主星在径向、切向和法向的速度增量分别为104.86, 93.82和27.3 m/s，而从星1在3个方向的速度增量分别为107.58, 93.68和94.86 m/s. 需要注意的是，通过调节控制器参数可以进一步提高相对精度，但代价是要提供更加频繁的机动和更高的燃料消耗，故需要根据实际应用场景来确定是采取燃料最优的策略还是性能最优的策略.

图3 卫星编队星下点轨迹图Fig. 3 Illustration of the ground tracks of satellites

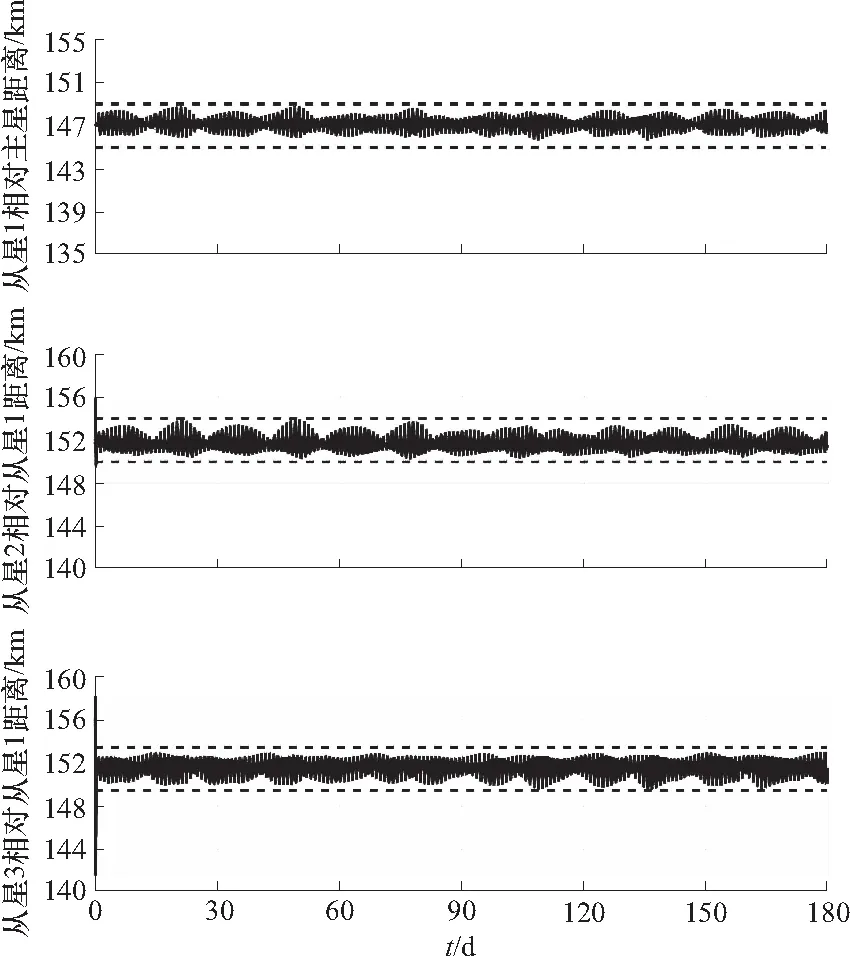
图4 编队卫星间相对距离Fig.4 Relative distances between leader and follower satellites

4 结 论

本文主要研究针对静止轨道卫星编队构型保持的模型预测控制方法. 对于采用线性化轨道相对动力学模型所产生的模型不确定性问题，通过设计误差管道，实现了卫星编队的鲁棒控制. 仿真结果表明，所设计的鲁棒控制器能够很好地克服空间环境摄动以及模型不确定性，实现静止轨道卫星编队的构型保持. 本文控制器设计采用的是连续变推力的推力模型，下一步可以开展脉冲推力模型以及继电型推力模型的研究，同时针对性地进行优化设计，实现高精度、低消耗的构型保持方法.