正定矩阵流形上的系统控制算法

纳文, 孙福鹏, 曾澍楠, 孙华飞

(北京理工大学 数学与统计学院，北京 100081)

对于非线性问题如果强行利用线性方法处理，可能带来很大误差，达不到必要的精度. 几何方法在处理非线性问题时发挥重要的作用. 把所研究的非线性问题纳入几何框架，在流形上每一点处的切空间上定义内积-黎曼度量，使之成为黎曼流形，就可以给出几何刻画，利用黎曼梯度算法求解定义在黎曼流形上的目标函数的最优值. 本文利用黎曼几何研究正定矩阵系统的控制问题. 在文献[1-8]中，作者们设计了随控制系统，使得系统的输出所服从的概率密度函数与事先指定的目标越接近越好. 其中利用了信息几何的方法，特别是利用了Fisher信息矩阵充当黎曼度量，把Kullback-Leibler散度作为所谓的距离函数，并给出了算法. 对于上述问题，由于经典信息几何理论框架的制约，上述算法无法给出更加深入的研究. 另一方面，矩阵信息几何的主要载体是一般线性群的子流形或李子群，黎曼几何、拓扑学、纤维丛、代数拓扑、李群与李代数等深刻的数学都可以发挥作用. 目前，信息几何用来研究非随机的非线性问题，并在图像处理、信号处理等方面获得了成功的应用. 作为启发，在文献[9-14]中，作者利用矩阵信息几何的思想，设计了输出是正定矩阵的控制系统，使得输出与事先指定的目标越接近越好. 其中，充分利用了矩阵信息几何优越性，即把正定矩阵全体看成黎曼流形，并引入了仿射的黎曼度量来定义测地距离，在该测地距离意义下给出问题的自然梯度算法，模拟仿真结果说明了算法的效果. 一个问题是：能不能给出更好的距离函数来求解上述问题. 本文利用对数欧氏梯度方法给出改进的新算法，关键是在正定矩阵流形以及每一点的切空间建立等距同构，使得正定矩阵流形成为一个欧氏空间，进而定义对数欧氏距离，使得算法更加简单.

1 正定矩阵流形上的几何结构

本文将正定矩阵全体看成一般线性群GL(n,R)={A∈Rn×n|det(A)≠0}的子流形. 由于正定矩阵具有良好的性质，特别地，其特征值均为正的性质使得矩阵分解具有很好的结果，在图像处理、信号处理等领域获得成功地应用. 用SPD(n)表示n×n正定矩阵所构成的微分流形，对于同一个流形可以定义不同的黎曼度量使之成为不同的黎曼流形. 定义特殊的黎曼度量-欧氏度量

gA(X,Y)=tr(XY)

(1)

式中X,Y∈TASPD(n),A∈SPD(n).

在文献[10-11]，作者们提出了仿射黎曼度量

gA(X,Y)=tr(A-1XA-1Y)

(2)

经过计算，可以获得连接SPD(n)上任意两点的测地距离

(3)

在文献[11]中，作者们利用指数映射在SPD(n)上定义乘法运算

AB=exp(logA+logB)

(4)

在SPD(n)上定义黎曼度量

gA(X,Y)=tr(((dlog)AX)T(dlog)AY))

(5)

式中d表示对数映射的微分.

经过计算可获得连接SPD(n)上任意两点A,B的测地距离

d2(A,B)=tr(logA-logB)2

(6)

在文献[12]中，根据建立纤维丛上的水平子空间与底流形SPD(n)的切空间之间的等距映射，给出了新的黎曼度量以及测地距离. 基本想法如下：建立GL(n,R)与SPD(n)之间的黎曼淹没

(7)

可以获得一个直和分解

(8)

由于等距保持测地线和测地距离，SPD(n)上的局部测地距离可由GL(n,R)上的测地距离来表示. 由于GL(n,R)上任意两点的测地距离可以由欧氏距离定义为

(9)

则可得到SPD(n)上任意两点A,B的测地距离

(10)

2 控制系统及其算法

本文假设系统输出仅由控制输入决定. 设x=[x1x2…xm]∈Rm为输入变量，则系统输出满足P(x)∈SPD(n). 本文的目标是设计输入x，使输出y接近给定的目标Q(正定矩阵). 此外，希望获得从初始矩阵P(x0)到最终矩阵P(x*)的控制轨迹.

图1 控制系统Fig.1 Control system

为了描述输出矩阵P(x)和目标矩阵Q之间的距离，将测地距离作为它们之间的度量. 因此，目标函数得到如下

J(x)=J(P(x))=d2(P(x),Q)

(11)

正定矩阵系统的最佳输出x*满足

(12)

设输出流形S={P(x)|x=[x1x2…xm]∈Rm}是SPD(n)的子流形,P(x)是控制输出矩阵. 下面给出算法.

对于定义在欧氏空间上的目标函数，则可以利用梯度下降法求解其最小值. 但对于定义在黎曼流形上的目标函数，此时的梯度方向已经不是欧氏空间的梯度下降方向，黎曼梯度才是最速下降方向. 因此在研究黎曼流形上函数的最优值时要考虑黎曼梯度. 具体表达如下.

命题1设f:M→R是一个光滑函数,g是黎曼流形M上的黎曼度量. 则有下面的求解f的最小值的迭代公式

θt+1=θt-λgradf(θt)

(13)

注1从命题1可以发现，自然梯度中要含有黎曼度量g，而且出现了求逆运算. 但是在矩阵流形上定义适当的黎曼度量，可以简单地表达黎曼度量.

注2无论利用欧氏梯度法还是利用黎曼梯度法求解目标函数的最小值时，都要陷入所求的的最小值不是整体最小值，而是局部最小值的问题，除非目标函数是一个凸函数.

既然在文献[9-10]中，作者们已经利用仿射黎曼度量给出了问题的求解过程，在本文中，分别利用定义在SPD(n)上的对数欧氏度量以及基于纤维丛黎曼度量给出问题的求解过程. 对于定义在SPD(n)上的黎曼度量，事实上，由于对称矩阵全体所形成的流形与SPD(n)的等距关系，SPD(n)成为平坦的流形. 利用欧氏梯度来计算定义其上面的目标函数的最小值.

命题2设目标Q∈S，则有梯度下降算法

(14)

式中：η为迭代步长,J(xt)为式(11)中的距离函数

J(xt)=d(P(xt),Q)=tr(logP(xt)-logQ)2

(15)

具体计算上述距离函数的梯度，可获得梯度J(xt)的分量

(16)

把式(16)带入式(14)可以获得计算上述目标函数的最小值.

命题3设目标Q∈S，则有梯度下降算法

xt+1=xt-λgradJ(xt)

(17)

式中：λ为迭代步长；gradJ(xt)为函数J(xt)的自然梯度；J(xt)为式(11)中的距离函数

J(xt)=d(P(xt),Q)=tr(P(xt))+tr(Q)-

(18)

从文献[14]可知，对于定义在在SPD(n)上的光滑函数f，在这种由纤维丛诱导的度量下其自然梯度可以表示为

(19)

利用式(19)可以得到梯度grad(P(xt)),从而得到算法的具体迭代公式.

总结上述过程，则有下面的算法.

命题4对于控制输入u=[x1x2…xm]有如下的步骤：

④ 增加t的值，再转到步骤②.

3 模拟仿真

在下面的例子中，将模拟命题2给出2种算法，允许的误差为10-5. 在第1个例子中，输入矩阵和目标矩阵为给定的3阶正定矩阵，在第2个例子中，输入矩阵和目标矩阵为随机生成的10阶正定矩阵.

例1假设目标B是输出子流形的一点. 选取三维正定矩阵

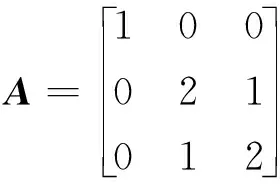
(20)

给定输出矩阵

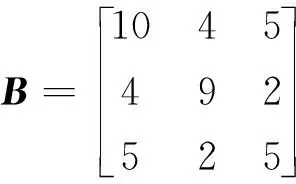
(21)

根据命题2，可以得到从A到B距离的轨迹，如图2. 在图2中可以清晰看到基于纤维丛的黎曼梯度在时间和收敛速度上都明显优于其他两者，对数欧式梯度比黎曼梯度收敛速度略慢，但是所用的时间却大大减少，这是由于对数欧式梯度简化了黎

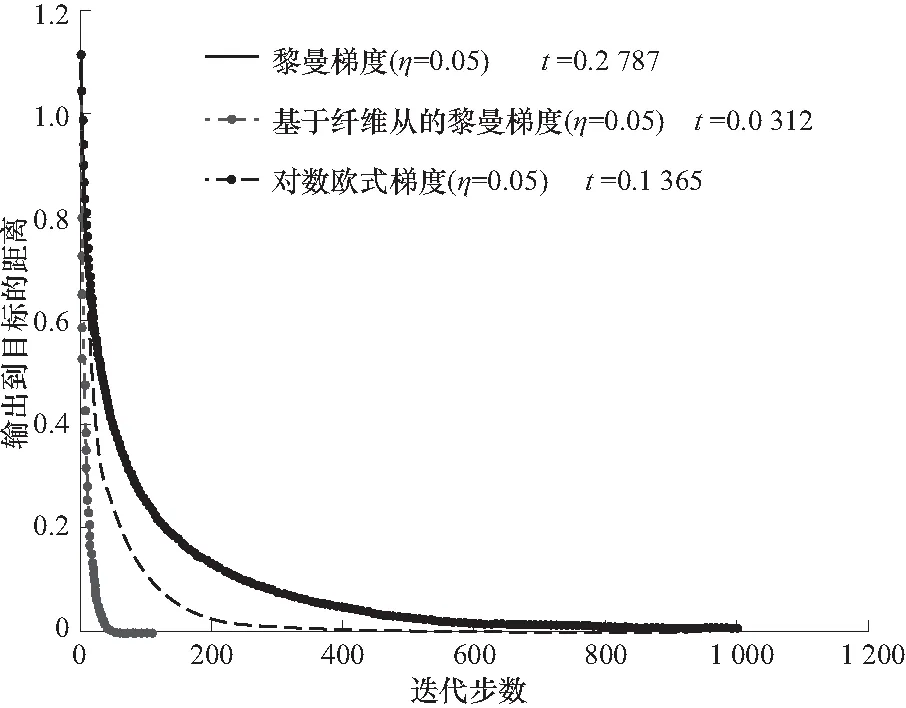
图2 输入矩阵到输出矩阵在3种梯度下的轨迹(3阶)Fig.2 The trajectory from the input to the target under three gradients(3rd order)

曼梯度中复杂的求逆运算，使得运算效率大大提高. 模拟得到的结果与预期相同.

本文将学习速度分别设定为0.05，0.20，0.40，得到的对数欧式梯度和基于纤维丛的黎曼梯度的收敛速度如图3.

图3 对数欧式梯度和基于纤维丛的黎曼梯度的收敛性Fig.3 Convergence of logarithmic euclidean gradient and Riemannian gradient based on fiber bundle

例1将随机生成的2个10阶正定矩阵分别作为输入和输出. 根据命题2得到从输入到输出距离的轨迹，如图4. 从图4中可以看到基于纤维丛的黎曼梯度的收敛速度依然最优，对数欧式梯度的收敛速度快于黎曼梯度，这说明随着输入和输出复杂度的改变，对数欧式梯度的优势已经开始显现.同时本例说明命题2给出的算法不依赖于初值和终值的选取，具有很好的普遍性.

图4 输入矩阵到输出矩阵在3种梯度下的轨迹(10阶)Fig.4 The trajectory from the input to the target under three gradients(10th order)

4 结 论

根据定义在正定矩阵流形上的对数欧氏度量以及基于纤维丛的黎曼度量，本文给出了正定矩阵流形系统的控制问题的求解过程. 与仿射黎曼度量相比，这两个度量下测地距离的形式简单，求解速度比仿射黎曼度量的方法快. 问题的解决过程涉及深刻的李群与李代数、纤维丛的巧妙应用，为解决类似的问题提供了参考.