一种基于统计流形的聚类算法

孙华飞, 宋扬, 罗翼昊, 孙福鹏

(北京理工大学 数学与统计学院,北京 100081)

传统的聚类方法，特别是K平均算法，严重依赖数据集的自身结构，无法将距离较远的同类数据聚为一类，并且抗噪能力有限，很难将随机出现的噪声与有效数据隔离开来[1-2].

一种自然的想法是利用邻域密度的差异对数据进行分类[2-5]. 本文利用局部统计将坐标信息转化为局部统计量以反映局部结构，将局部统计量相近的数据聚为一类. 具体地,用局部统计量作为参数确定一个特殊的参数分布，将所有数据点投射到参数分布所在空间(即参数分布族)得到参数点云. 构造分布族上参数点的方法较大程度地涵盖了原点云的局部信息，同时参数分布族的流形结构便于更精细的数据分析. 最后依据参数点云的聚类结果，对原始点云进行分类.

本文分别考虑多元正态分布族流形上的欧氏距离、Wasserstein距离和KL散度[6-9]，并应用K平均算法，对参数点云聚类. 注意到对于非欧氏度量，K平均算法中涉及的重心不一定是算术平均，本文将分别讨论欧氏距离、Wasserstein距离和KL散度的几何平均.

最后，本文对含高密度噪声的斯坦福兔子点云数据进行去噪实验，讨论基于不同度量K平均算法的实验效果.

1 局部统计

在n维欧氏空间n中，记规模为m的点云为C:={pi∈n|i=1,2,…,m}.对任意的p∈C，采用k近邻方法选取邻域N(p,k)，简记为N. 之后计算邻域N内数据点相对位置的均值E[N]-p和协方差Cov[N]，分别记为μ(N)和Σ(N). 最后，将数据点表示为n元正态分布族流形Nn中的参数点，其中

Nn=

(1)

由此定义局部统计映射

Ψ:C→Nn

(2)

满足

Ψ(p)=

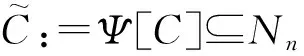
2 高斯分布族上的度量和KL散度

(3)

(4)

2.1 欧氏度量

由于Nn和n×SPD(n)拓扑同胚[6]，可以通过定义n×SPD(n)上的度量结构，诱导出Nn上的度量.

DE((μ1,Σ1)，(μ2,Σ2))=‖μ1-μ2‖2+

‖Σ1-Σ2‖2

(5)

2.2 Wasserstein度量

(6)

式中∏(P1,P2)为2n上以P1,P2为边缘密度函数的联合分布的全体. 特别地，对于多元正态分布的情形，文献[8]给出了显式表达式.

命题1[8]任意两个多元正态分布间的Wasserstein距离为

(7)

由于Wasserstein度量的几何平均依然是有待解决的问题，在K平均算法实现中，本文用算术平均来代替几何平均.

2.3 Kullback-Leibler散度

Kullback-Leibler散度(KL散度)是概率分布间常用的差异函数，定义为

DKL(P1||P2)=EP1[logP1-logP2]

(8)

特别地，对于任意两个n元正态分布P1,P2∈Nn，通过计算得到

(9)

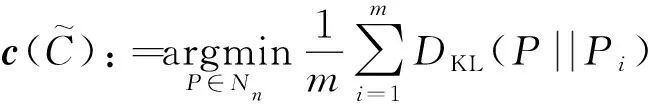
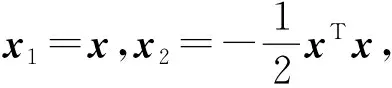
P(x;μ,Σ)=P(x1,x2;θ)=

exp{tr[(x1,x2)(θ1,θ2)T]-φ(θ)}=

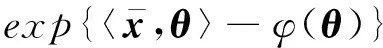
(10)

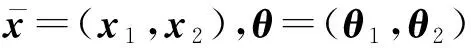
借助多元正态分布族上的Bregman散度，给出KL散度的几何平均. 由凸函数φ(θ)诱导的Bregman散度定义为

(11)

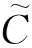
证明首先证明对任意P1,P2∈Nn，DKL(P1||P2)=Bφ(P2||P1)，φ为自然参数θ下的势函数.

由

得到

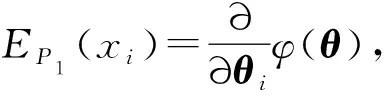
DKL(P1||P2)=EP1[logP1-logP2]=

Bφ(P2||P1)

(12)

在以KL散度作为差异函数的K平均算法实现中，定理确保参数点云的几何平均可由参数变换后的算术平均显式给出.

3 SKM算法

图1 SKM算法流程Fig.1 SKM algorithm flow

SKM算法：

输出：点云C的一个K划分.

SKM算法是K平均算法在统计流形上的推广，其效能依赖于差异函数的选择.

4 SKM算法的点云降噪及模拟仿真

点云降噪是工业界和学术界许多工作讨论的重点. 本章节选取不同的差异函数，考察SKM算法在去除高密度噪声实验中的效果.

实验原数据采用斯坦福兔子三维点云的下采样，背景噪声服从均匀分布，真实噪声比为1 500∶3 000.真实点：噪声点，如图2.

图2 原始点云Fig.2 Original data cloud

本次实验采用k=5,K=2,ε=0.01的SKM算法，其中2个初始重心为

由于KL散度和几何平均都涉及到矩阵求逆,本文对局部统计中得到的协方差矩阵增加0.1倍的单位矩阵,进行非退化处理，以防止奇异矩阵计算时出现的过大误差.

本文采用正确率(accuracy)、查全率(recall)和查准率(precision)来刻画算法的去噪效果. 实验结果如表1.

表1 去噪效果Tab.1 Denoising effect

图3～图6分别展示了基于KL散度(几何平均)和KL散度(算术平均)、欧氏距离和Wasserstein距离(算术平均)的SKM算法对原始点云去噪后的图像.

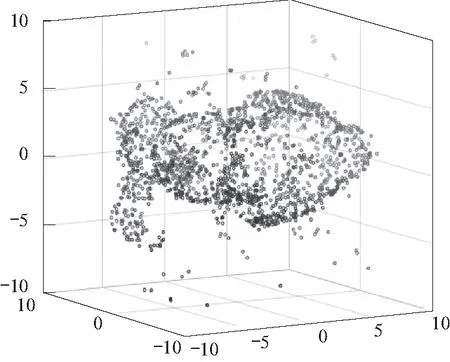
图3 基于KL散度(几何平均)方法去噪后点云Fig. 3 Point cloud after denoising based on KL divergence(geometric mean)

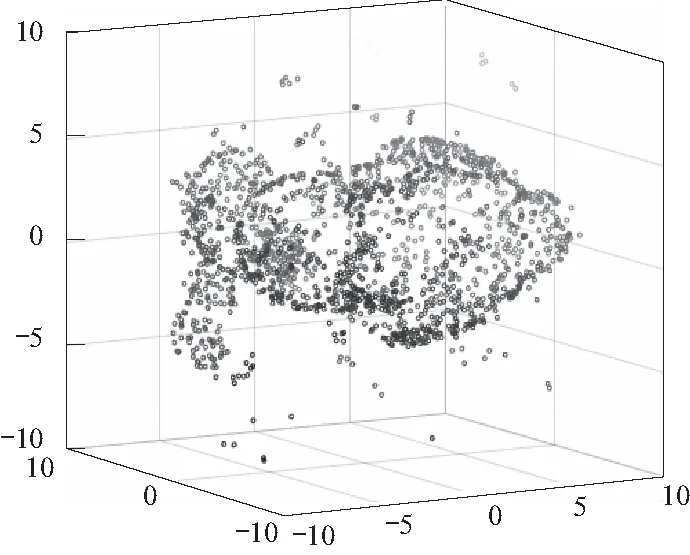
图4 基于KL散度(算术平均)方法去噪后点云Fig.4 Point cloud after denoising based on KL divergence(arithmetic mean)

图5 基于欧氏距离方法去噪后点云Fig.5 Point cloud after denoising based on Euclidean distance

图6 基于Wasserstein距离方法去噪后点云Fig.6 Point cloud after denoising based on Wasserstein distance

在本次实验中,基于KL散度的SKM算法去噪效果明显，且用算术平均代替几何平均依然得到了较好的实验结果. 欧氏距离和Wasserstein距离(算术平均)方法的去噪效果较差. 实验表明，欧氏距离不能很好地刻画密度函数间的差异，而算术平均不能很好代替Wasserstein几何平均可能是实验结果较差的原因.

同时本次实验显示出SKM算法具有良好的收敛性，特别地，基于KL散度几何平均的算法收敛速度最快，如图7.

图7 重心更新差异与迭代步数的关系Fig.7 Relationship between the difference of barycenter renewal and the number of iteration steps

5 结 论

本文用局部统计表示原始数据，设计了一种基于统计流形上的差异函数SKM聚类方法. 在含高密度背景噪声的斯坦福兔子去噪实验中，SKM算法有良好的收敛性. 并且发现采用KL散度的SKM算法的去噪效果，能够达到较高的准确率、查全率和查准率，体现出SKM算法在去噪应用中的潜力.