让数学思维看得见

曹宇

[摘  要] 数学的抽象性、概括性较强，使得数学学习时需要学生展开较高强度的思维活动。能触碰、操作的实物，以及看得见的图画，可以让学生的思维过程显现得更加生动和形象。因此，有必要在小学数学教学中引入思维可视化教学模式，让学生参与更生动、更形象的数学学习过程，让数学學习更高效。文章认为，可以从创设可视化场景、鼓励动手操作、展开思维过程、教师提示点拨这些方面入手，运用思维可视化教学模式，实现高质量的小学数学教学。

[关键词] 小学数学;思维;可视化;实施策略

小学数学是一门思维性很强的学科，若不会思考或思考能力不强，则很难将数学学好。如何能实现高质量的数学教学，培养学生成为思维能力、解决问题能力很强的学生呢？如何让学生成长为核心素养很强的人才呢？这需要结合小学生的身心发展特点进行教学。小学生以形象思维为主，看得见、能感知或触碰的具体实物，以及可见的图画等，可以让他们更高效、准确地理解数学空间与数字;而且这些可视化的教学元素可以吸引小学生的注意力，让数学学习变得形象、生动，不再枯燥，有趣好玩。因此，可以将思维可视化教学模式引入数学教学中，打造高效、生动的小学数学教学模式，为培养更优质的人才服务。

一、思维可视化教学模式的概念及应用意义

1. 思维可视化教学模式的概念

思维可视化教学模式是指利用具体的事物学习数学的方法。具体的事物可以是图画、模型，也可以是教具以及生活中常见的其他实物等。数形结合（画图分析）、学具操作或生活实物操作等都是可视化学习方法。

2. 思维可视化教学模式的应用意义

思维可视化可以让数学学习更加生动。小学生以形象思维为主，生活实物、学具、图画等能提高学生参与思维分析的兴趣;另外，学具操作或生活实物操作、画图分析等可以让学生更直观、形象、准确地分析数学问题，展开清晰的思维过程，实现高效学习。在具体的生活实践中，如果能运用身边看得见、摸得着的工具，将抽象的数学知识演变成轻松有趣的可视化场景，那么学生的理解力、创造力和思维力等将得到最大化的提升！

二、思维可视化教学模式的具体实施策略

1. 结合生活实际，创设可视化场景

单纯的、大篇幅的文字，以及纯粹的口头语言难以吸引小学生的注意力，而且小学生难以轻松、高效地理解这些文字和口头语言。小学生以形象思维为主，结合小学生的发展特点，可以基于小学生的生活实际，借助于学具、生活实物等，创设轻松有趣的可视化场景，提升学生参与数学学习与思维活动的兴趣。教师需要先了解学生的认知基础、生活经验，再做好材料准备、科学预设，最终创设可视化场景。

案例1：“分数的初步认识（二）”教学片段

课前，教师准备好一篮子干净、新鲜的桃子，上课时将其放到讲桌上吸引学生的注意力。这些桃子是用来干什么的呢？学生纷纷交头接耳。

生1：是有什么好玩的事情吗？

生2：是来分桃子吃吗？

师：是来分桃子哦！今天我们利用桃子来学习分数。

环节1：

师：老师这里有一些桃子，家里有2个人想吃桃子，平均每人能分到多少呢？

教师邀请了3名学生上讲台，分别从篮子中拿出了4个、6个、8个桃子放在3个盘子里，然后将4个、6个、8个桃子都平均分成了2份。教师将学生分出的结果通过画图的方式展示在黑板上，让全班学生进行观察。

提问：（1）分成相同的份数，为什么每份桃子的个数不同呢？

（2）每份桃子的个数不同，为什么都用来表示呢？

借助于桃子的实物操作过程和黑板上的图画，学生很清晰地发现，因为每盘桃子的个数（所选桃子的总数）不同，所以即使分成相同的份数，每份桃子的个数也不同;但都是平均分成了2份，所以都可以用来表示。

环节2：

之后，教师再邀请学生运用桃子、盘子进行操作，教师提问。

师：如果总共有6个桃子，有3个人来吃，该怎么分呢？

提问：（1）把6个桃子平均分成2份，每份是它的（   ）;

（2）把6个桃平均分成3份，每份是它的（   ）。

把物体平均分成不同的份数，表示每份的分数也就不同。

环节3：

师：我们来对比一下，每份的分数有什么奥秘。

将4个、6个、8个桃子都平均分成2份，每份桃子分别为2个、3个、4个。虽然每份桃子的个数不同，但都可以用来表示。得出：表示的分数相同（分成的份数相同），但总体数量不同，每份的数量不同。

将6个桃子平均分成2份，每份有3个;将6个桃子平均分成3份，每份有2个。得出：总体数量相同，分成的份数不同，每份的数量不同。

小结：分数指整体的一部分，表示每份数量占总体数量的几分之几，每份数量与总体数量的大小有关，也与分成的份数有关。

教师借助于实物操作和画图等手段创设可视化情境，为学生经历思维可视化的过程奠定了基础，学生能轻松、形象、生动地理解分数的概念、分数表示的意义。思维可视化的辅助工具有生活实物、学具、图画等，教师有时可以综合运用。

2. 提供工具材料，鼓励动手操作

教师准备好可视化素材并创设了可视化情境后，还需要尽可能地给学生提供一些自主动手操作的实物工具、学具，以及图画分析、自主观察、独自思考的机会。在操作过程中需要学生运用到大脑、双手和眼睛等。教师提供动手操作的机会，鼓励学生自主动手操作，能使学生全身心投入可视化的思维过程。这就是“教学做合一”理念的践行要求。唯有亲身经历自主动手操作的过程，才能真正了解问题的前因后果，知晓知识的由来与发展。

案例2：“有余数的除法”教学片段

教师将学生分成6人一组，让学生拿出10支铅笔作为学具。

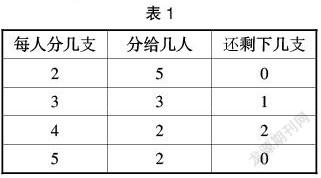
师：10支铅笔，每人分2支，能分给几人？每人分3支、4支、5支，分别又能分给几人？小组内分一分，在表格里记录下来。

学生运用铅笔参与自主动手操作的过程，小组内成员一起合作，完成分配，并将结果（数据）记录在表格中（如表1所示）。

之后，学生会根据结果（数据）分析“平均分刚好分完”“平均分有剩余”的知识点。依托动手操作，引导学生认识“余数”。

后续，教师还可以设计12根、13根、14根、15根、16根小棒分别拼摆正方形：能拼摆几个正方形，余下几根小棒？

依托这个环节的动手操作，引导学生认识“余数总比除数小”。

“教学做合一”理念指出，需要让学生在“做中学”。依托生活实物、学具或图画，让学生参与动手操作的过程，为学生提供思维可视化的机会，学生会边操作、边思考、边讨论交流，分析问题并记录过程和结果（数据），获得真切的学习体验。生活实物、学具等是学生思维的辅助工具，依托生活实物和学具展开清晰、具体的思维过程，学生在头脑里能形成画面，获得深刻理解。

3. 给予时间和空间，展开思维过程

创设可视化情境、组织实践操作过程，都是为学生思维可视化服务的。学生动手操作的过程是思维可视化的一部分。另外，教师还应该给予学生充足的时间和空间，让学生静下心来经过动手操作、实物展现、画图等，完成思维可视化的过程。学生可以在摆弄、再次操作、观察图画等方法下，展开高阶思维，利用直观形象分析问题和探寻答案。

案例3：“角的初步认识”教学片段

教师展示与角有关的生活实物，如三角尺、钟表（时针与分针）、园艺工人的剪刀、足球场的边界、小红旗的边角等，给予学生分小组合作观察、讨论的时间。观察、分析之后，由教师设置任务。

任务：用线条画出这些实物的边框轮廓。

学生拿出尺子动手绘画，画出了各种三角形。之后，教师再给予学生充足的时间和空间思考问题。

师：其实，这些都是角，角有什么特点呢？

学生依托实物和图形，结合刚才画角的经历进行思考。

生3：角要是尖尖的，旁边的线要是直直的。

师：是的，你回答得非常好！

教师再展示一些实物，组织学生参与“是不是角”的判断。师生一起小结，归纳出儿歌：角的顶点尖尖的，角的两边直直的，不尖不直不是角。

教师给予学生利用生活实物、学具等进行思考的空间与时间，学生参与了思维可视化的过程，更清晰地理解了什么是角、什么不是角。形象、直观的可视化辅助元素，让数学学习更轻松、有趣，达到高质量的教学。

4. 教师提示与点拨，实现问题的解决

在学生展开动手操作、思维可视化的过程后，教师需要针对学生的实践操作、思考过程与收获、结论等，进行恰当的点拨与提示，让学生获得可视化学习的收获;教师需要针对学生的闪光点、发现点、不足处与存在的问題等进行点拨与提示。帮助学生将思维变得更加准确、清晰，依托可视化思维发现问题并解决问题，总结出新知识点，发现数学规律，探讨出数学思想和方法。

案例4：“平移、旋转和轴对称”教学片段

教师组织学生参与动手剪纸活动，学生剪出了漂亮的蝴蝶、花朵、三角形等，并思考轴对称图形的特点，以及各种图形的对称轴有几条，等等。

教师借助于图画、生活实物等提示学生什么是对称轴、什么是轴对称图形，教师一边展示、一边提示与点拨，最后总结知识点。

师：对称轴是一条直线，沿着这条直线对折，图形能完全重合。轴对称图形，指的是整个图形沿着对称轴对称。

教师的提示与点拨，让学生思维可视化的过程更清晰、正确;总结知识点，让学生把握住要点，且收获数学思想和方法，实现高效、高质量的教学。

三、结束语

“让数学思维看得见”。教师应基于小学生的身心发展规律，结合数学学科的特点，利用可视化的生活实物、学具等工具，让学生的头脑里形成形象、直观的画面，让学生经历思维可视化的过程，获得真切的学习体验，实现高效学习、轻松学习。把握住图画绘制与展示，以及利用生活实物、学具等动手操作的几个关键要素，能让思维可视化教学模式在小学数学教学中运用得当，提升教学质量。

3435501026549