条件引领思路展开 教学微设激发思维
程中曜


[摘 要] 问题探究要注重两方面内容:一是注重对问题条件与图像的拆解;二是注重思路构建的方法,这也是教学指导的关键点. 下面以一道抛物线综合题为例,进行思路突破,并结合教学实践,提出相应的建议.
[关键词] 解析几何;定值;面积;反思;微设计
[⇩] 问题呈现,考点分析
问题:已知直线l的解析式为2x-y-4=0,与x轴的交点为E,抛物线Ω的方程为y2=2px(p>0),点F为抛物线的焦点,其中点O为坐标原点,且=,回答下列问题.
(1)试求抛物线Ω的方程.
(2)如果直线l与抛物线Ω相交于点P和B(点P在第一象限),直线PA与抛物线的交点为A,与x轴的交点为D,直线PC与抛物线的交点为C,与x轴的交点为G,且点E为DG的中点. 设直线PA和PC的斜率分别为k和k,试证明+为定值.
(3)在(2)的条件下,试求△PBC面积的取值范围.
考点分析:上述是关于抛物线与直线相交问题,涉及了向量、直线斜率、面积模型等知识. 第(1)问求抛物线的方程,考查抛物线方程的求法;第(2)问证明+为定值,实则考查抛物线与直线相交、直线斜率构建;第(3)问求三角形面积的取值范围,考查抛物线中三角形面积的构建方式,以及取值范围分析方法等.
[⇩] 思路突破,过程评析
问题突破需要把握考点,合理构建图像来逐步分析转化,下面逐问探究.
(1)由直线l的解析式可求得点E(2,0),由向量条件=可知点F为OE的中点,故点F坐标为(1,0). 所以=1,可解得p=2,则抛物线的方程为y2=4x.
(2)联立抛物线Ω与直线l的解析式,有2x-y-4=0,
y2=4x,可求得点P(4,4),B(1,-2),点E是DG的中点,则+=0,可设点D(2-t,0),点G(2+t,0),其中t>0. 结合点坐标可求直线斜率,有k=,k=,则+=+=1,可证+为定值.
(3)可将△PBC视为是以点C为顶点,PB为底边的三角形,则S=×PB×d,其中d表示点C到直线PB的距离. 在(2)的条件下,则直线PC的方程为y-4=(x-4),整理可得4x-(2-t)y-4t-8=0,与抛物线的方程联立,可得y2-(2-t)y-4t-8=0,可解得y=-t-2或y=4(舍去),所以x=,即C
,-t-2
,故点C到直线PB的距离为d==. 由点P和B的坐标可得PB==3,所以关于△PBC的面积函数为S=×3×=.
设过点P的抛物线的切线方程为y-4=k(x-4),联立y-4=k(x-4),
y2=4x,可得ky2-4y+16-16k=0,由Δ=0可得k=,所以切线方程为x-2y+4=0,令y=0,可得x=-4,所以要使过点P的直线与抛物线有两个交点,需满足条件2-t>-4,则有0<t<6.
综上可知,S=,其中0<t<6,则0<S<54,所以△PBC面积的取值范围为(0,54).
[⇩] 教学探讨,创新微设
上述抛物线综合题涉及了众多考点,所涉三问相互独立,又紧密关联,且难度逐问递增,在实际教学中建议采用数形结合的方式,引导学生从问题出发,理解题意,绘制图像,逐步构建思路. 下面具体探讨数形结合的构建方式,以及创新微设计的环节引导.
1. 数形结合图像构建
考题的第一问是基础问题,后两问是核心之问,构建图像有助于条件转化和思路构建.
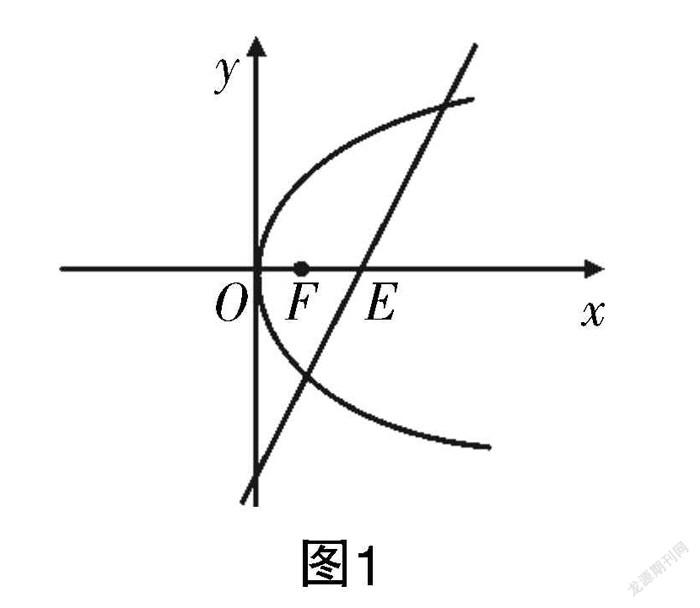
第(1)问是关于直线l与抛物线Ω的相交,根据向量条件“=”可知点F为OE的中点,故可根据该信息绘制图像,主要包含两个信息:直线l与x轴的交点为E;点F是OE的中点. 可绘制图1所示图像.
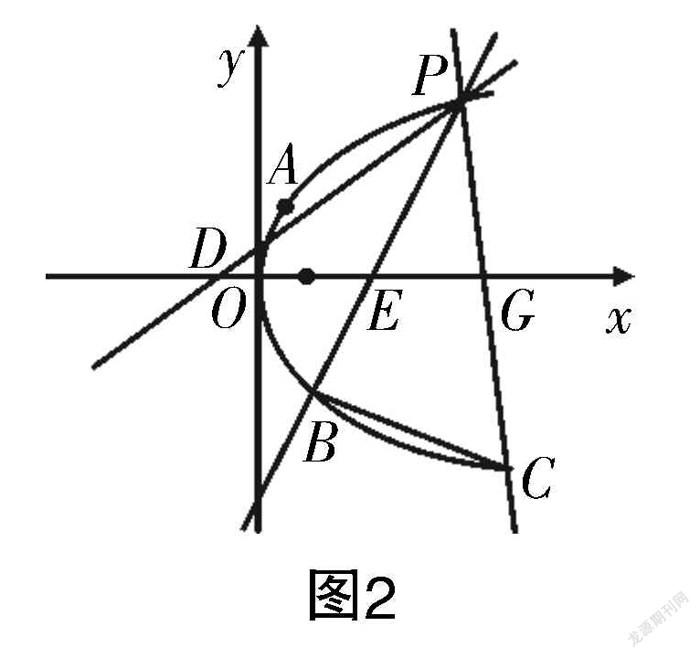
第(2)问涉及众多直线与抛物线相交,总体上有三条直线,且直线之间存在相对关系:直线l与抛物线Ω相交于点P和B,直线l位于中间;直线PA与抛物线交于点P和A,直线在左侧;直线PC与抛物线交于点P和C,直线在右侧. 由此可绘制图2所示图像.
第(3)问是在(2)问基础上的构建,以交点为基础构建了△PBC,需要关注其中的两个信息:直线PA与抛物线有两个交点;直线PC与抛物线相交于点P和C.
2. 创新微设计引导环节
实际教学中建议采用“微设计”的方式,让学生逐步感受考题构建,通过设问引导的方式指导学生思考问题,转化条件,体验思路构建. 下面分三大环节进行教学设计,由浅入深,深刻理解问题.
环节(一)——基础巩固,初绘图像
题设:已知直线l:2x-y-4=0,与x轴的交点为E,抛物线Ω:y2=2px(p>0)的焦点为F,其中点O为坐标原点,且=.
设问1:从向量“=”中可以获得哪些位置关系和数量关系?
设问2:试求点F的坐标,并求出p的值.
设问3:根据直线l的方程确定与坐标轴的交点,结合点E和F的位置绘制图像.
教學引导:引导学生确定点F的坐标,确定抛物线的方程参数p,求解方程,然后把握直线与抛物线的位置关系绘制图像.
环节(二)——能力强化,关系探究
题设:根据如下信息绘制图像.
信息1:直线l与抛物线Ω相交于点P和B(点P在第一象限);
信息2:直线PA与抛物线的交点为A,与x轴的交点为D;
信息3:直线PC与抛物线的交点为C,与x轴的交点为G;
信息4:确保点E为DG的中点.
绘图过程引导学生思考如下问题:直线PB,PA和PC的相对关系;三条直线的交点P的位置;点E和点D,G的相对关系.
问题探究中引导学生合理设定坐标,构建直线斜率:
设问1:根据直线l与抛物线相交求点P和B的坐标.
设问2:E是DG的中点,则+等于多少?若设点D(2-t,0),如何表示点G?
设问3:请根据点P和D的坐标求直线PA的斜率k,根据点P和G的坐标求PC的斜率k,并求+的值.
环节(三)——知识综合,建模解析
题设:连接BC,构建△PBC,绘制相应的图像.
求△PBC面积的取值范围需要经历构建模型、转化面积函数、定义域分析三个阶段,教学可根据上述三阶段来设问引导.
设问1:若将△PBC视为是以点C为顶点,PB为底的三角形,可构建怎样的面积模型?
设问2:请根据点P和G的坐标表示直线PC的解析式,与抛物线方程联立求点C的坐标,设点C到直线PB的距离为d,利用“点到直线的距离公式”求d的值.
设问3:结合上述信息来构建△PBC的面积函数,S=×PB×d.
设问4:要使直线PA与抛物线有两个交点,则与过点P的抛物线的切线方程有怎样的位置关系?过点P的抛物线的切线与x轴的交点为(-4,0),则点D(2-t,0)与(-4,0)有怎样的关系?可得出哪些结论?
设问5:请根据上述△PBC的面积函数及关于参数t的取值范围求面积的取值范围.
[⇩] 解后反思,教学建议
上述基于一道抛物线综合题进行了解题突破、教学探讨,整个过程侧重解题思路的构建,培养学生的數学思维,下面深入反思,提出几点建议.
1. 无图问题提信息,精心构图探方向
部分解析几何问题没有给出图像,但问题又涉及众多的曲线特征和几何性质,分析难度较大,因此理解题意,精准构图是突破的关键. 教学中建议首先指导学生绘制图像,然后进行思路构建. 构图环节需要注重两点:一是引导学生明辨条件与结论,提取图像信息;二是转化文字信息为几何信息,根据几何语言来绘制图像. 后续的探究分析则只需立足图像特征,采用数形结合的方法探讨突破方向即可.
2. 解后反思评过程,结构分析生策略
教学中要注重解后反思,引导学生反思解题过程,分析问题结构,生成合理的解题策略. 以上述问题为例,要引导学生总结问题类型、结构特点及问题解法. 必要时可开展“一题多解”“多题一解”,指导学生总结问题的“通性通法”,合理进行方法拓展,探究关联性问题的解法. 教学中要充分发挥经典问题的价值,利用考题探究来提升学生的能力.
3. 教学微设勤互动,追问对话促思维
解题教学建议采用“微设计”的方式,围绕考题开展微设计,将问题条件与结论拆解为多个模块,引导学生逐步探究,可帮助学生构建思路,形成正确的解题思维. 而“微设计”环节需要采取“互动探究”与“追问对话”相结合的方式,重视学生的主体地位. 设置具有启发性的问题,让学生在互动思考中“生成”观点,通过追问对话促发学生新的“思想”.
3727500589221

