压电式动态力传感器校准方法的研究

卢小犇,翟琼劼,屠 淳,范海艇,胡红波

(1. 上海市质量监督检验技术研究院，上海 201114; 2. 中国计量科学研究院，北京 100013)

随着中国经济持续发展，城市的综合提升中，汽车、智能制造、生物力学、高铁和地铁等轨道交通将扮演着极为重要的角色[1]。如今在“中国制造2025”以及“一带一路”的政策引领下，我国的这些相关行业进入了一个前所未有的快速发展通道。

这些领域需要使用大量的压电式传感器来承担状态监视、故障报警、设备控制等功能，它们是保障高速运行的交通工具或者机械装置安全可靠使用的前提[2]。由于压电传感器表征的动态性能指标种类繁多，本文重点对其中的动态力学性能进行研究。

目前国内外在压电式传感器的动态力学性能校准上主要分为两种[3-4]，第一种是正弦力校准，第二种是脉冲力校准。目前国际上尚无统一规范化动态力校准的标准化文件，在实际的工程应用中，传感器用于正弦力测量的条件要求比较少，更多的情况是用来做装置或者设备运行过程中的状态监测，异常碰撞或者摩擦产生的脉冲力往往是工程中更需要捕捉的工程量，所以对传感器进行脉冲力校准往往有更强的应用需求。

本文根据项目任务的要求对压电式传感器建立了数学模型，同时针对传感器动态力性能校准的方法从正弦力法和脉冲力法两个角度通过理论模型分析，比较两者的差别，最后根据脉冲力法建立了一套动态力校准装置，并通过实验对该装置的校准方式进行了方法论证，得到了较为满意的结果。

1 压电式传感器校准的数学模型

1.1 正弦力校准方法及模型

就目前国内外现状而言，正弦力与脉冲力是两种最常用的校准传感器动态力的方法。正弦力法是通过激振器对动态力传感器进行正弦激励，校准的任务就是对激励后传感器所受到的特定频率的循环力进行幅值和相位特性的分析[5]，结构简图与模型如图1所示。

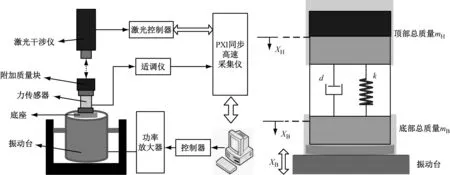
图1 正弦力校准结构简图与结构模型Fig.1 Schematic diagram of sinusoidal force calibrationstructure and structural mode

传感器的输出信号可以等效为与两个质量块相对位移成正比例关系，即

X=XB-XH

(1)

(2)

将式(1)代入式(2)中，可得：

(3)

(4)

等式两边同时进行拉氏变换后得到传递函数如式(5)所示

(5)

从式(5)可以看出，此时动态力传感器的传递特性可视作一个一阶的传递系统，最终的校准结果会随着质量块附加质量的变化而变化。当干涉仪的测量点从传感器的顶端转移到安装表面的时候传递函数则如式(6)所示。

(6)

式(6)属于相关拓展内容，为一个二阶系统，可用于分析动态力传感器的结构响应特性。我们在实际校准工作中只能测量传感器的顶端运动情况，同时我们的校准目标是希望得到传感器的输入输出关系而不是关心传感器的结构特性所以我们采用式(5)所示的形式。

1.2 脉冲力校准方法及模型

本文重点介绍的脉冲力法是通过脉冲力发生装置对传感器施加单次脉冲，产生的波形通常为半正弦波，通过对脉冲的峰值采集和波形分析来校准传感器的动态力性能并计算灵敏度[6]。

用脉冲力法校准动态力传感器的装置因为目前没有国际统一的标准规范，所以现有的设计特点大多参考ISO 16063—13所介绍的冲击加速度测量方法中提出的校准装置[7]，常见的有落锤式或摆锤式脉冲力发生装置等。

从式(1)不难看出，压电式动态力传感器在冲击力作用下也可以等效为一个单自由度的模型，其特性可用一个二阶微分方程来表征[8]，等效的结构模型如图2所示，主要包括四个部分，底部质量mB、顶部质量mH以及与联系两者的弹簧k和阻尼d。

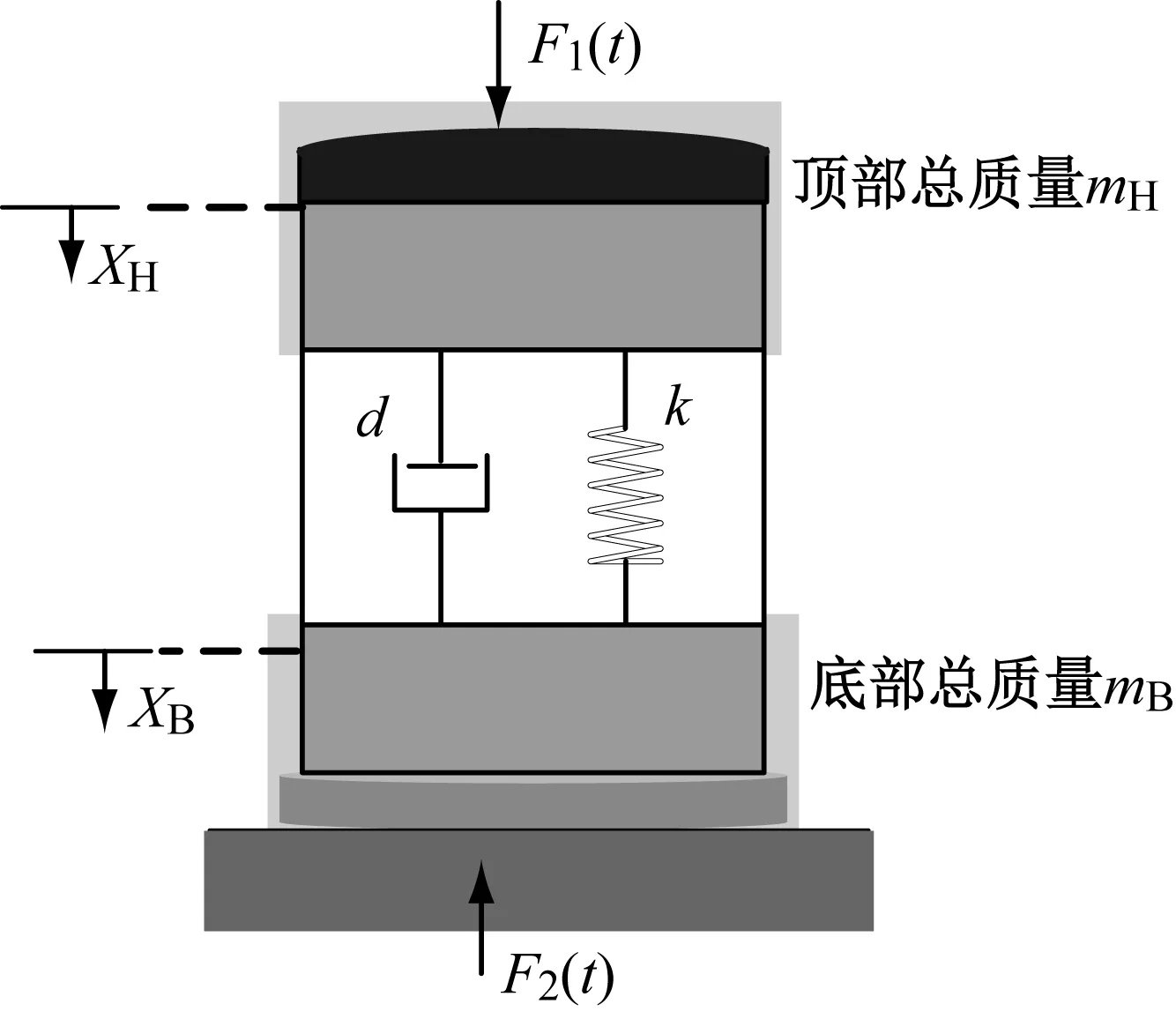
图2 传感器脉冲力校准结构模型Fig.2 Structural mode of the sensor pulse force calibration

根据牛顿第二定律，我们在校准传感器动态力学性能时需要在传感器表面安装质量块用以计算传感器所受到的脉冲力，我们需要确保质量块和传感器属于刚性连接，以确保整个系统的弹簧k和阻尼d不变，这样可以确保用不同附加质量块所得到的校准结果具有可比性，图中两个质量是传感器自身质量与质量块质量之和。

图2中F1(t)与F2(t)分别作用在传感器的顶部与底部，其顶部与底部的运动方程如式(7)所示。

(7)

将式(1)代入式(7)并做变换，可得式(8)。

(8)

式(8)表示的是传感器的在脉冲力作用下的输入输出方程，是一个二阶传递系统，两边进行拉氏变换即可得到相应的传递函数。与正弦力分析方法类似在实际校准过程中由于不需过多考虑传感器的内部结构响应，故与式(5)类似，我们可使用式(7)中第一个方程作为传感器的传递函数。

1.3 结 论

通过对两种方法的模型分析我们不难总结出如下特点：

传感器动态力的校准需要考虑的因素非常多，主要来自校准条件，不同质量不同大小的质量块，不同的固定螺栓连接强度，不同的安装底座都会对最终的校准结果产生影响。同时不同的测量手段大到使用干涉仪或者标准加速度计等方法的选择，小到干涉仪测量点的选取抑或标准加速度计的安装刚度安装位置的选择都会对整个系统的结构模型产生影响。因而在后续校准不确定度分析过程中以上因素都应要作为重要影响分量进行评估。

两种方法都可以较好的诠释传感器的动态特性，方法的选取主要还是取决于传感器本身的使用环境，正弦力法更适合在循环力作用下的传感器校准且具有较高的校准精度，而脉冲力法适合应用于冲击碰撞环境下的传感器校准，可以覆盖更宽的频带，而重复性会相对交大[9]。

2 基于刚体碰撞的脉冲力发生装置

本文参考了针对冲击加速度测量的国际标准ISO 16063-13中提出的设计理念同时也参考了国外同行实验室相关的装置[10-12]，研制了如图3所示的高精度脉冲力发生装置，也是国内首套依据该理论模型设计的脉冲力发生装置。

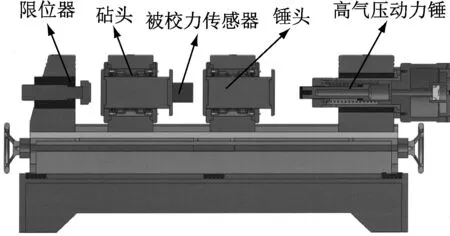
图3 脉冲力发生装置Fig.3 Impulse force generator

如图3所示装置的结构如下：整个系统的动力源在最右侧，是一个由压缩空气驱动的高压弹簧动力锤，动力锤冲击端有缓冲橡胶垫；依次往左是锤头和砧头，砧头与锤头通过空气轴承悬浮支撑，可沿轴向无摩擦自由运动，是两个质量相当的圆柱体；锤头左端可安装不同材质的缓冲试验垫，如硬质橡胶或者羊毛毡，砧头右端有法兰盘及配套连接件用于安装固定被校动态力传感器，最左侧则为一个限位器，限位器上打有通孔以确保激光干涉仪可以通过该孔照射到砧头左端以测量传感器及砧头的运动情况，从而实现绝对法脉冲力的测量。系统运行方式为冲击锤撞击锤头，带动锤头加速，在空气轴承的悬浮下匀速撞击传感器，结合缓冲试验垫的应用使整个传感器砧头系统产生瞬时的完整脉冲加速度，最后运动至限位器停止。该装置较现有装置的优势如下：

(1) 采用水平卧式结构，整体尺寸结构较现有垂直立式结构小；

(2) 质量单元采用气浮轴承来支撑质量块，气浮轴承能提供非接触式无摩擦支撑，使质量块可在水平方向自由移动，减少了质量块在碰撞过程的动能损耗，同时能起到精确平稳导向的作用；

(3) 激励单元采用压缩空气驱动动力锤来对质量单元(锤头)产生瞬时动能，可以较小的尺寸结构获得较大的力值；

(4) 激励单元的空气炮驱动动力锤，配合质量单元的气浮轴承支撑锤头，解决了现有垂直立式结构的质量单元不能无摩擦释放的问题；

(5) 质量单元采用两块质量块，分别为锤头和砧头，两块质量块分别由气浮轴承支撑，这种结构使得两块质量块的运行轨迹有很高的控制精度，并且使其在碰撞过程的动能损耗的侧向分量降到最低。

3 基于外差式迈克尔逊干涉仪的测量系统

对于刚体碰撞的脉冲力发生装置，常用的加速度测量方法常见的有比较法和绝对法，比较法是选用加速度计及动态信号分析仪来测量砧头的整个加速度脉冲波，本系统为了进一步提升装置的测量精度，选用了基于外差式迈克尔逊干涉原理的激光绝对法来测量加速度。干涉仪多普勒信号依据ISO 16063-13标准推荐的方法实现对碰撞过程中脉冲加速度量的测量，解算方法如图4所示。

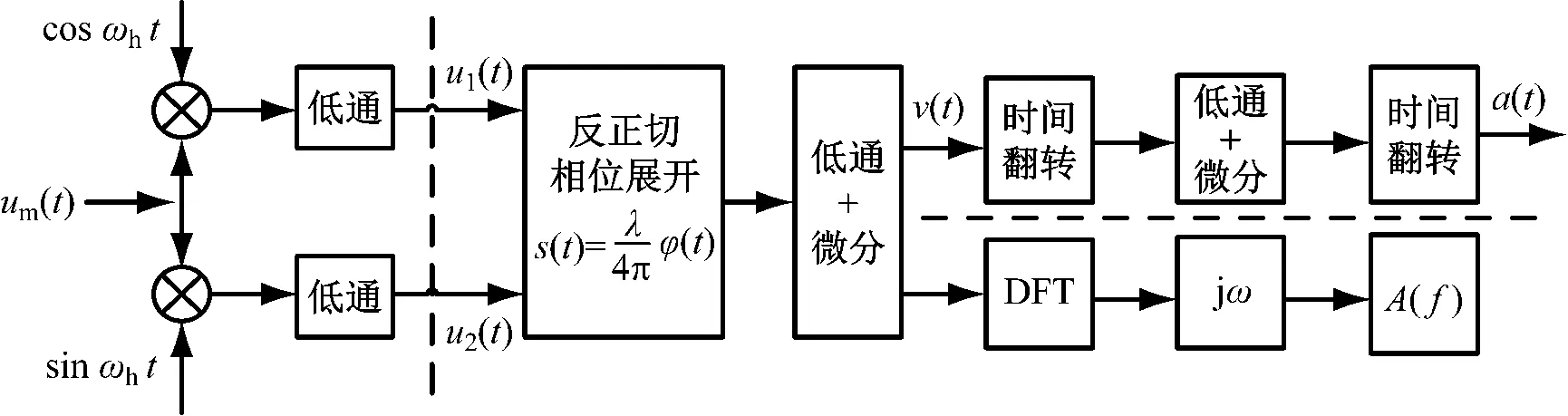
图4 激光干涉信号的解算过程Fig.4 The solving process of laser interference signal

当我们精确测量得到整个活动部件的加速度，同时结合我们在试验开始前就已经通过精确称量得到所有安装部件的质量之和，然后通过牛顿第二定律就可以得出施加在动态力传感器上的脉冲力，这就是本文介绍的压电式动态力传感器的脉冲力绝对法校准。

4 试验结果及分析

根据压电式传感器的数学模型通常我们会认为在校准时传感器的输入和输出之比即灵敏度是一个常数，整个系统可以视作一个等比例模型，所以传感器动态力校准的核心内容就是测得传感器的灵敏度，并对在不同的校准条件下所测得灵敏度进行一致性分析。

动态力传感器的结构刚度k一般都能达到108以上N/m，数值较大，而等效的阻尼系数d一般为103～104次方kg/s，再结合式(5)所示的针对作用于传感器端部的动态力传递模型，可以把动态力传感器的传递特性等效为一阶传递函数。鉴于传感器本身的工程特性和使用领域特性，常使用频段较低的工程，使得式(5)中的s变得非常小，可将该式近似等效为如式(9)所示。

(9)

本装置的测量系统在激光干涉仪后端采用美国NI公司的PXI多通道高速信号采集分析系统，分析软件的编写在美国NI公司LabVIEW虚拟仪器软件环境平台上，在实际校准过程中通过多通道高速信号采集分析系统，我们将激光干涉仪采集到的信号与被校传感器自身捕捉到的信号呈现在同一时间轴上，并进行比较分析。

干涉仪输出信号按照图4所示算法计算，得到的脉冲速度与加速度信号分别如图5所示。

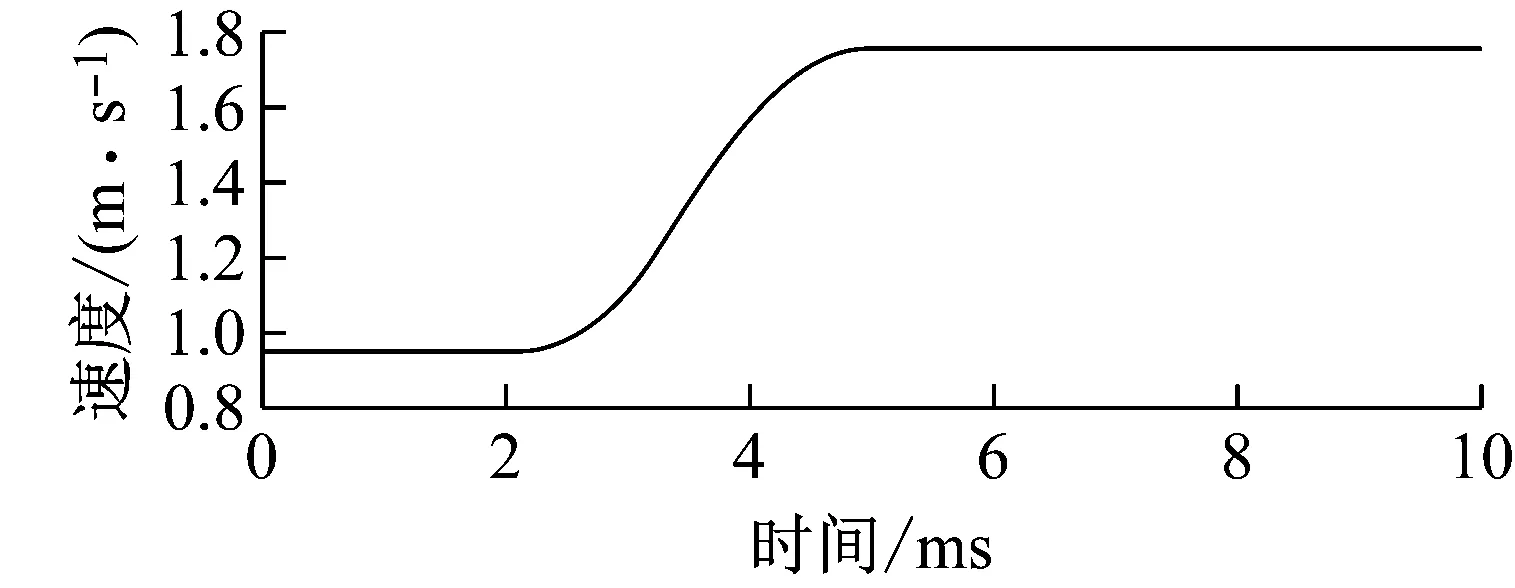
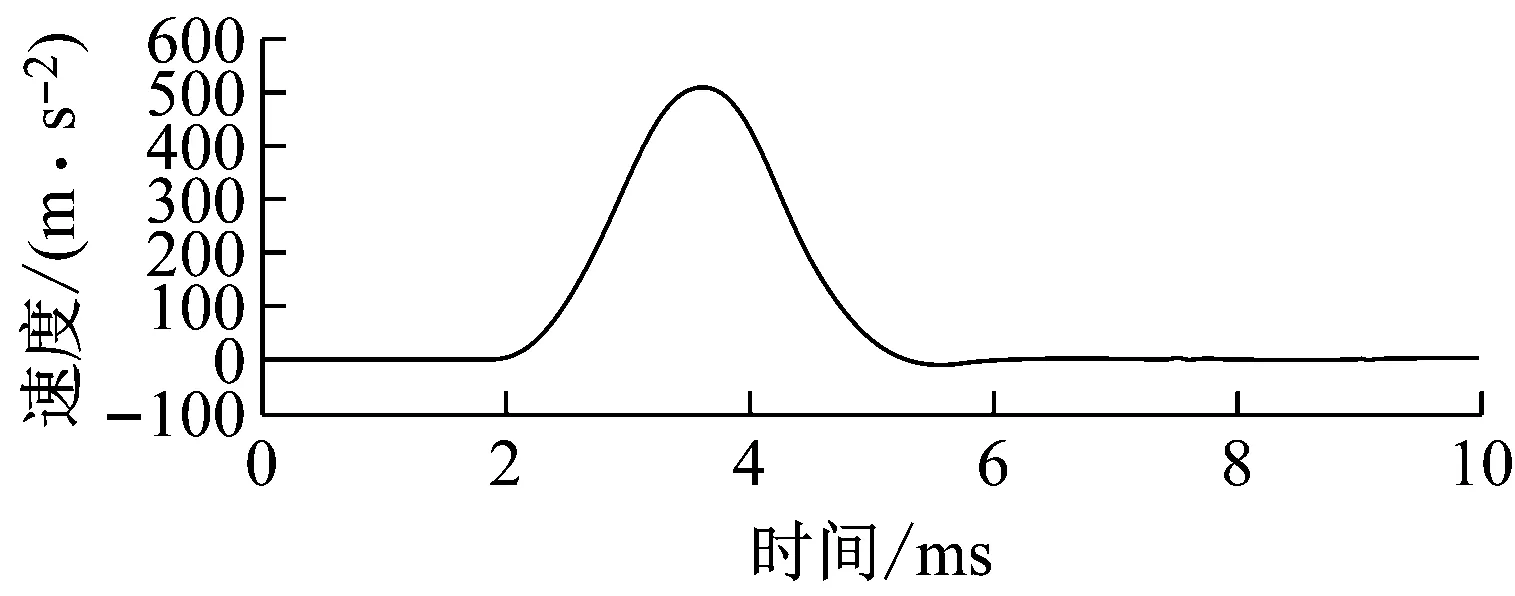
图5 脉冲速度与加速度信号Fig.5 Signals of pulse velocity and acceleration

在试验过程中被校压电式传感器被刚性安装在砧子上，在整个运动过程中可视为一个整体，将这一部分的整体质量乘以图5所示的加速度峰值就得到了在压电式传感器上施加的脉冲力值。本装置中砧头和被校压电式传感器的质量总和为2.145 kg，加速度峰值为521.2 m/s2，通过计算得出相应的脉冲力峰值为1 118.0 N，对应的脉冲持续时间为3.35 ms。

图6 脉冲力校准试验方法Fig.6 The impulse force calibration methods

在上述试验方法下对瑞士KISTLER公司某一型号的压电式力传感器进行如图6所示脉冲力校准，结合电荷放大器的放大倍数做归一化运算后的得到一组校准数据如表1所示。

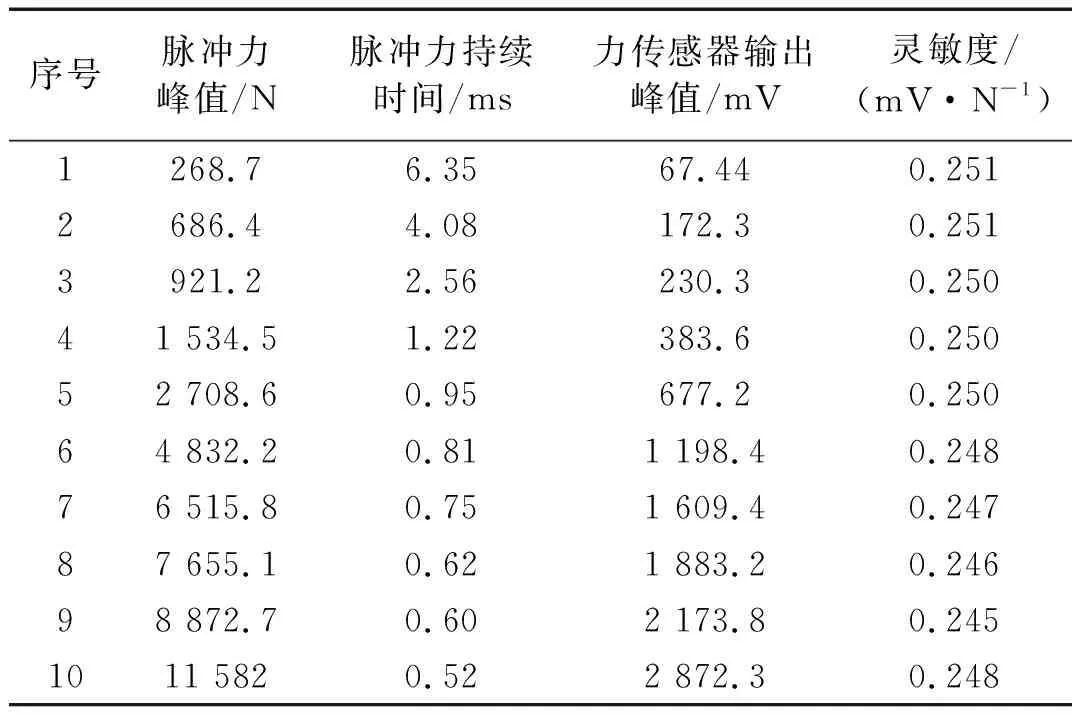
表1 力传感器校准结果

根据表1中的试验数据及其不确定度评估结果，同时根据前文分析结论，压电式传感器在常规校准条件下可视作等比例模型，结合中心极限定理，同时认为实际校准过程中的噪声为高斯分布，最终利用加权最小二乘法将被校动态力传感器的输入输出信号拟合成直线，该直线的斜率与截距分布如图7所示。

对拟合得到的直线进行简单计算不难得出直线斜率的最佳估计值为0.249 8 mV/N，置信概率为95%的区间为[0.247 9，0.251 7]。同理得出直线截距的最佳估计值为0.895 1，置信概率为95%的区间为[-0.490，2.282]，从分析结果中不难看出不确定度偏大，出现这个情况的主要原因在于表1中所得的校准结果是通过计算一阶线性方程的斜率来确定，而截距对校准结果的影响则相对较小，也就是数据保护关于斜率的信息较多。图8为其拟合的直线图，图中圆圈代表实际校准的数据，两条虚线之间的区间则代表拟合直线置信概率为95%的区间。

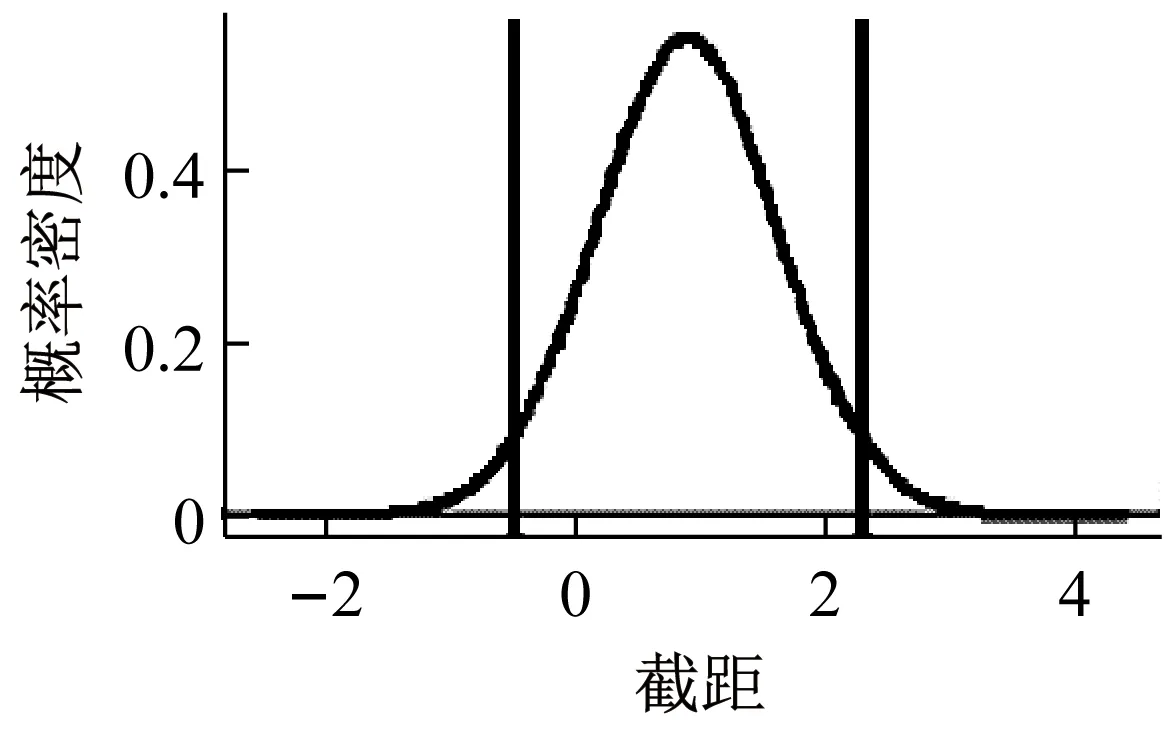
图7 拟合直线截距与斜率的概率分布Fig.7 The probability distribution of the fitting line interceptand slope

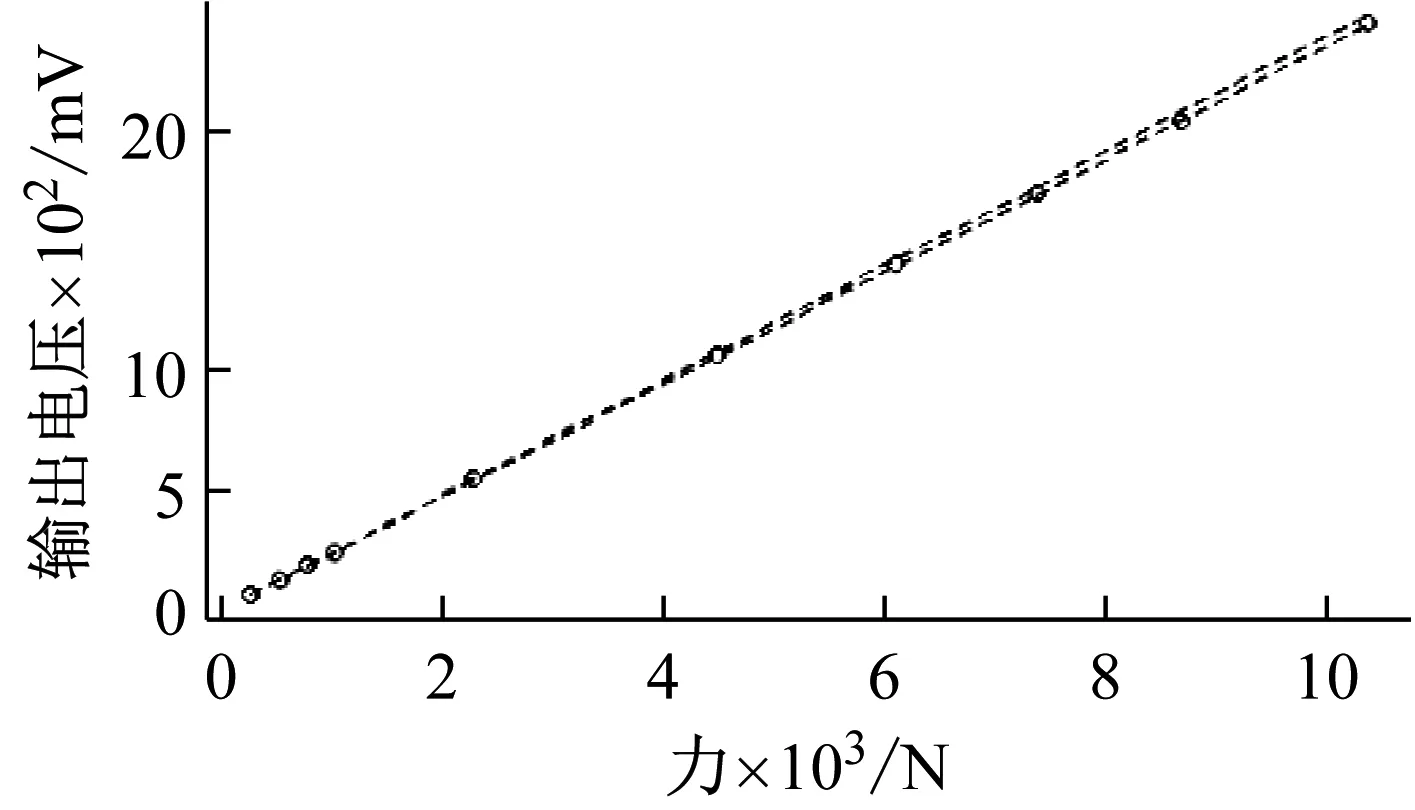
图8 实际校准结果与拟合直线置信区间Fig.8 Calibration results and the fitting line confidence interval

5 结 论

本文针对智能制造行业领域内对于压电式传感器的动态力学性能校准的需求介绍了对应的校准方法与标准加载装置的试制与研究。首先根据压电式传感器的结构特性和运动特性建立了压电式传感器的数学模型和运动方程，然后有针对性的介绍了压电式传感器动态力校准的两种方法并结合传感器的数学模型和运动方程，对不同校准方法和校准条件下的传感器校准结果进行了较为详细的理论分析，并给出适用条件的解析。然后选取比较典型的脉冲力校准法，重点介绍了一种基于绝对法测量、横向气浮冲击结构的脉冲力法校准装置，阐释了设计中的相关结构和工作原理，同时还介绍了外差式激光干涉仪的测量原理和解算方法，给出了绝对法测量的理论依据。

最后选取典型的被校样品型号在新建立的标准装置上进行校准试验并对试验结果进行分析，对压电式传感器的脉冲力校准结果比较满意，充分验证了本装置和方法的可靠性，不过在智能制造领域传感技术的应用非常广泛，压电式传感器也只是其中很小的一部分，其中的动态力校准和可靠量值溯源性也只是传感器动态性能校准中的部分内容，实际应用中存在进行基于动态力传感器模型参数辨识的校准、传感器阶跃力校准以及动态校准结果的评估等[13]相关需求，以上这些都是动态产业计量校准，先进制造业在线校准，原位计量领域内有关于动态性能的主要研究方向，本装置的研制和方法的确立也为进一步研究相关内容奠定了基础。