基于性能衰退评估的轴承寿命状态识别方法研究

董绍江，吴文亮，贺 坤，潘雪娇，蒙志强，汤宝平，赵兴新

(1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆大学 机械传动国家重点实验室，重庆 400032； 3.重庆长江轴承股份有限公司，重庆 401336)

轴承作为现代制造业的重要组成部分，在大多数旋转机械的运行中发挥着至关重要的作用。轴承寿命状态识别对机械系统的可靠性和安全性具有重大意义。但滚动轴承的寿命状况受各种因素影响，难以识别。因此，研究滚动轴承寿命状态识别方法显得非常重要。

近年来，数据驱动方法运用在轴承故障诊断、性能评估、剩余寿命预测等诸多方面。 在寿命识别领域，数据驱动方法试图使用机器学习技术从测量信号中推导出机械的衰退过程，根据衰退过程对寿命状态进行识别。轴承寿命状态识别存在两个必须解决的问题：如何构建合适的轴承性能衰退指标；如何建立有效的轴承寿命状态识别模型。

合适的轴承性能衰退指标必须充分利用复杂的信号特征，能够在轴承性能衰退的各个阶段获得轴承的性能演变。在机械故障诊断中有多种指标，如峰值指标、裕度指标、峭度指标等。Wang等[4]使用了原始振动信号的14个时域特征来捕获衰退特征。Boškoski等[5]提出了采用Rényi熵作为特征指标。Chen等[6]将均方根用于评估轴承性能下降。然而，这些指标要么对早期轴承缺陷不够敏感，要么后续稳定性不足。常用的指标针对不同的振动特性，仅对特定阶段的特定缺陷有效。张康等[7]通过降维算法建立盾构装备刀盘多传感器数据与其健康状态的关系，实现了刀盘性能衰退状态的有效量化评估。但该方法无法直接运用于复杂的轴承振动信号，需要先在原始信号中提取有效特征。近年来CNN在深度学习方法的研究中展示了提取复杂轴承特征的能力。因此，本文提出了由CAE提取原始信号特征，再通过MDS算法降维，以低维特征空间构造的欧氏距离为轴承性能衰退指标。

目前，数据驱动的轴承寿命状态识别模型不断被提出。数据驱动的方法在精度和复杂性方面提供了折中的选择，Ben Ali等[8]提出了模糊自适应共振理论映射(SFAM)神经网来进行轴承的寿命状态识别和预测。Benkedjouh等[9]运用等距特征映射约简技术(isomap)和支持向量回归(SVR)模拟轴承退化的演化过程，预测轴承的寿命状态。这些模型在轴承的寿命状态识别方面取得了不错的效果，但是这些模型没有考虑噪声干扰的情况，难以保证精度，因此本文提出了改进卷积神经网络轴承寿命状态识别模型，为增加样本数，抑制过拟合，对原始训练样本进行加噪，为提高模型抗干扰能力，并以LReLU函数和dropout作为激活函数。

本文提出了一种新的针对轴承衰退期寿命状态识别模型。将轴承信号通过CAE进行特征提取，将提取后的信号特征通过MDS算法降维，在低维特征空间构造欧氏距离作为评价轴承性能衰退指标。基于既定的指标构建CNN模型，最终实现轴承寿命状态识别。

1 轴承性能衰退指标的构建

在本文中，首先，利用卷积自编码器提取轴承信号特征，再将提取的特征通过MDS算法[10]降维，在二维空间中，将各个样本特征点到正常样本中心的欧氏距离作为轴承性能衰退指标，具体理论依据为：

卷积自编码网络是由编码和解码过程组成，编码过程是由高维原始数据向低维投影，如下

(1)

(2)

(3)

式中:λ为权重衰减系数;sl为第l层神元个数;m为样本数。

卷积自编码可获得I维的特征集合h={h1,h2,…,hI}，可得任意两样本特征之间的距离δi,j

(4)

δi,j可组成变量间的距离矩阵

(5)

将矩阵的第i行记为δi，MDS得到了一组大小为I的向量集{δ1,δ2,…,δI，δi∈RI}，矩阵的每一行对应RI空间中的一个向量，RI空间的维度代表原始变量与其他变量之间的距离。MDS算法是在保持变量间相对距离不变的基础上，寻找一个从数据集RI到RN之间的映射关系。最终，MDS将转化为计算式(6)的最优化问题

(6)

求解式(6)时，构建矩阵H，T，D，其中Hi为RN空间中第i个坐标点，tij为矩阵T中的元素，D为距离矩阵，dij为D中的元素。矩阵关系如式(7)所示

(7)

由式(7)可得

(8)

可得到距离矩阵D中元素与矩阵T中元素的关系

(9)

最后，对矩阵T进行特征值分解，如式(10)所示。其中U为特征向量，Λ为特征值矩阵。

(10)

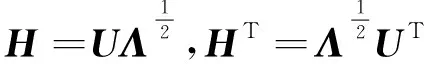
(11)

取H的前N个最大的特征值与特征向量对矩阵进行近似表示，即完成了从RI到RN空间的降维，可得到低维空间特征集{θ1,θ2,…,θN，θi∈RN}。

欧氏距离通常用于计算两点之间的距离[11]。在本文中，在二维空间中的样本数据与轴承正常期样本域中心的欧氏距离用来作为轴承性能衰退指标ID，值越大表示轴承衰退情况越严重，其算法如下

(12)

式中，θo为低维空间中正常期轴承信号特征。

2 轴承性能衰退评估

本节中运用数据集来证明所提指标的有效性，从测试中捕获信号，获取轴承寿命状态特征，构建轴承性能衰退指标，与其他方法的结果进行比较。

2.1 数据描述

试验数据集来自NSFI/UCR Center on Intelligent Maintenance Systems(IMS)。试验系统如图1、2所示。四个轴承安装在一个轴上，速度始终保持在2 000 r/min，通过弹簧机构将2 721.55 kg的径向载荷放置在轴上并轴承上。所有轴承都经过强制润滑，两个PCB353B33高灵敏度石英ICP加速度计安装在每个轴承上，共有八个加速度计。图1显示了测试设置并显示了传感器的位置。数据以20 kHz采样。试验数据详细介绍见文献[14]。

2.2 特征提取

本小节中，选取的是试验数据集中第1组轴承测试中的第3个轴承的x轴数据。完成样本处理后，利用卷积自编码器提取轴承信号特征，运用MDS算法进行降维，获得维度为二维的低维特征。将二维特征值分别作为横坐标和纵坐标，结果如图3(a)所示。为了进行对比，运用了流形算法t-SNE进行对比，其结果如图3(b)所示。为了方便比较，对结果进行了归一化处理。

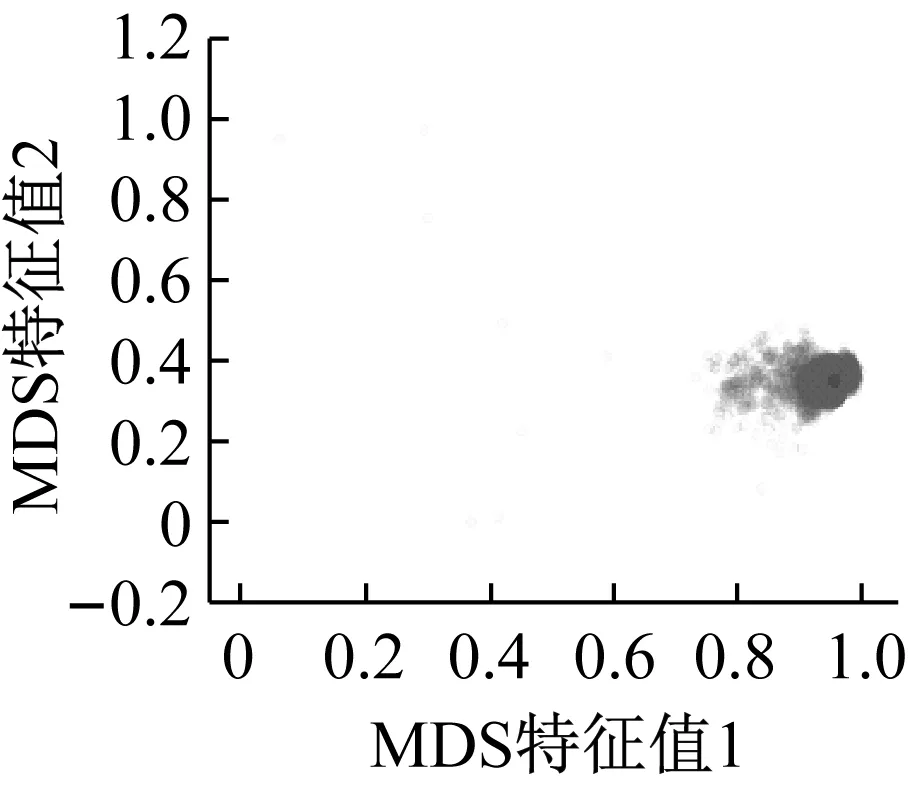
(a) MDS特征(b) t-SNE特征图3 特征降维结果Fig.3 Dimensionality reduction of result

试验以全寿命的样本作为输入，图3中包含了正常期、衰退期的数据。一般情况下，试验轴承刚开始采集的信号不稳定，因此，本文中规定在试验开始的第二天数据的特征中心为正常期样本域中心，即为图3中红色的点。根据相似度的降维思想，图3中向外偏离正常期样本域中心的特征点，损坏程度越高，颜色越深说明聚集程度越高。一般来说，轴承信号会有一段较长的正常期，可计算得到MDS特征点的离散度为0.046，t-SNE特征点的离散度为0.321 3，MDS特征点的聚合度更高，更符合轴承数据的特性。另外，离散度越大，所建指标的噪声水平和不稳定性越大，会导致对轴承性能状态的错误评估。MDS是线性降维，它保证的是在降维前后，特征点之间的距离一致，能够在低维特征中保留高维特征之间的相对关系，这也同时保留了高维特征从正常到重度变换的时序规律，但t-SNE是非线性降维，它保证的是降维前后，特征点的条件概率分布一致，非线性变换可能造成特征在时序规律上的变换，对指标的建立造成影响。因此，本文中将MDS用于降维。

MDS基于特征之间的欧氏距离进行降维，所以根据在二维空间中的欧氏距离构建轴承性能衰退指标最能体现高维特征之间的相似度。为说明根据欧氏距离构建指标的优势，将欧氏距离与马氏距离进行对比。欧氏距离只计算特征点之间直线距离，而马氏距离的建立基于全部特征点。首先，在低维特征空间中，获取轴承正常样本域中心，再将样本数据的二维特征点与正常期样本域中心的距离作为轴承性能衰退指标，结果如图4所示，图4(a)为基于MDS特征的欧氏距离结果，图4(b)为基于MDS特征的马氏距离结果，图4(c)为基于t-SNE特征的欧氏距离结果。

比较图4(a)与图4(b)，MDS特征的欧氏距离的方差为0.021 7，MDS特征的马氏距离的方差为0.026 9。马氏距离波动比欧氏距离大，可能会导致出现异常值，并增加了误判的可能，这说明欧氏距离更适于建立指标。比较图4(a)与图4(c)，轴承样本的损伤程度能够从基于MDS特征的欧氏距离上有效的反应，但在图4(c)中，虽然总体上能够反应轴承退化的趋势，但是在总体波动太大，对轴承性能评估能力较差，这可能是由于t-SNE算法的非线性变换造成了特征在时序规律上的变换。图4(a)中所提出的指标克服了其他方法的缺点，基于MDS特征的欧氏距离更能反应出轴承性能退化过程，所以，本文中采用了该方法构建指标，首先，将提取的特征通过MDS算法降维，在二维空间中，将各个样本特征点到正常样本中心的欧氏距离作为轴承性能衰退指标。

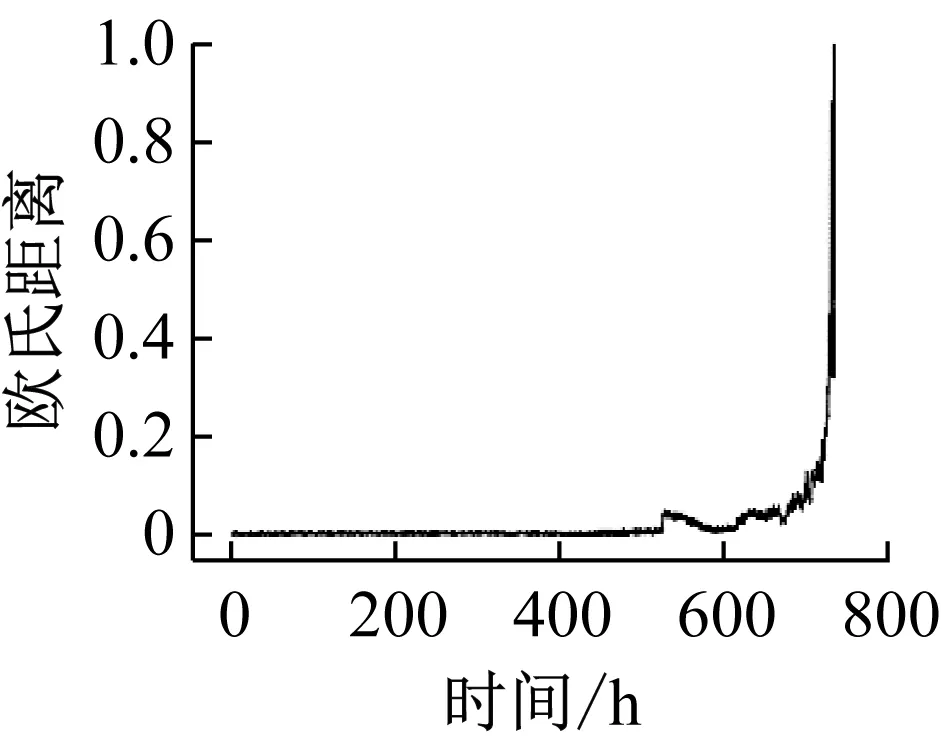
(a) MDS特征的欧氏距离(b) MDS特征的马氏距离

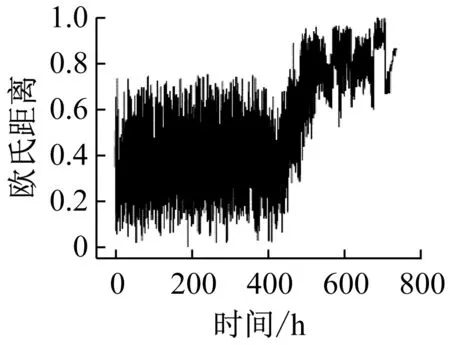
(c) t-SNE特征的欧氏距离 图4 降维特征在二维空间的距离Fig.4 Distance of dimensionality reduction feature intwo-dimensional space

为了验证本文中所构建的指标的优势，将所提出的指标，与最常用的均方根进行了比较，如图5所示。

图5 均方根指标Fig.5 Root mean square

从图5中可以看出，均方根指标的噪声水平和不稳定性都比本文中所提出的指标要大。在健康的轴承状况下，这会导致出现异常值，并增加了在检测初期退化时发出错误警报的机会。图5所示的均方根指标在600 h后的幅值变化较难区分，难以得出轴承早期退化阶段的明显结论。图4(a)所示的本文所提出的指标明显克服了这些缺点，比传统的均方根指标更有效。比较图4(a)、图5，可以得出结论，本文所提出的指标曲线在区分轴承的正常，轻微和严重退化阶段时更为直观。

3 CNN轴承寿命状态识别模型

本文中所提出的CNN识别模型，共建立19层模型，包括1个输入层，8个卷积层，8个池化层，1个全连接层，1个输出层。另外，本文为增加样本数，抑制模型过拟合，在原始数据中加入随机白噪声，为提高模型抗干扰能力，并以LReLU函数和Dropout作为激活函数。同时，通过批量归一化(batch normalization，BN)方法对数据进行处理。BN层使得输入到该层的数据落入敏感的非线性变换函数的区域中，以避免梯度消失。CNN详细训练过程见文献[14]。

3.1 数据集增强

数据集增强技术通过增加训练样本，已达到增强神经网络泛化性能的目的，对于轴承振动信号，由于其特有周期性，采用重叠采样的方法来增加训练样本的数量。另外，神经网络训练过程中很容易造成过拟合，导致所得到的网络对测试样本识别效果差，泛化能力弱。在有限的寿命样本输入中加入随机白噪声，减弱神经网络的联合适应性，学习到的特征区分度大，增强鲁棒性。同时，进行训练时，加入随机噪声相当于增加样本，减少神经网络过拟合。

3.2 改进激活函数

常用的激活函数是ReLU函数。ReLU函数解决了Sigmoid函数部分梯度爆炸和消失的缺点，计算和收敛速度都很快，但是针对轴承信号来说，ReLU函数将振动信号的负轴特征全部舍去，减弱了模型对轴承寿命状态的识别性能。因此，本文采用LeakyReLU(LReLU)函数，LReLU解决了ReLU函数在输入为负时产生的梯度消失的问题。另外，针对噪声干扰问题，模型通过增加Dropout层来增强抗干扰能力。Dropout使得神经元节点之间的关节适应性的减弱，同时起到类似于数据集增强的作用，减少过拟合。因此，原有的ReLU由LReLU和dropout代替，其算法如下：

LReLU(xi)=max(aixi,xi)

(13)

ri～Bernoulli(p)

(14)

yi=ri*LReLU(xi)

(15)

式中:LReLU(·)是Leaky ReLU激活函数;ai是LReLU函数负半轴斜率;ri是由遵循相同伯努利分布的几个独立变量组成的向量;p是某个神经元存活的概率。最终，可构建轴承寿命状态识别模型，其结构如图6所示。

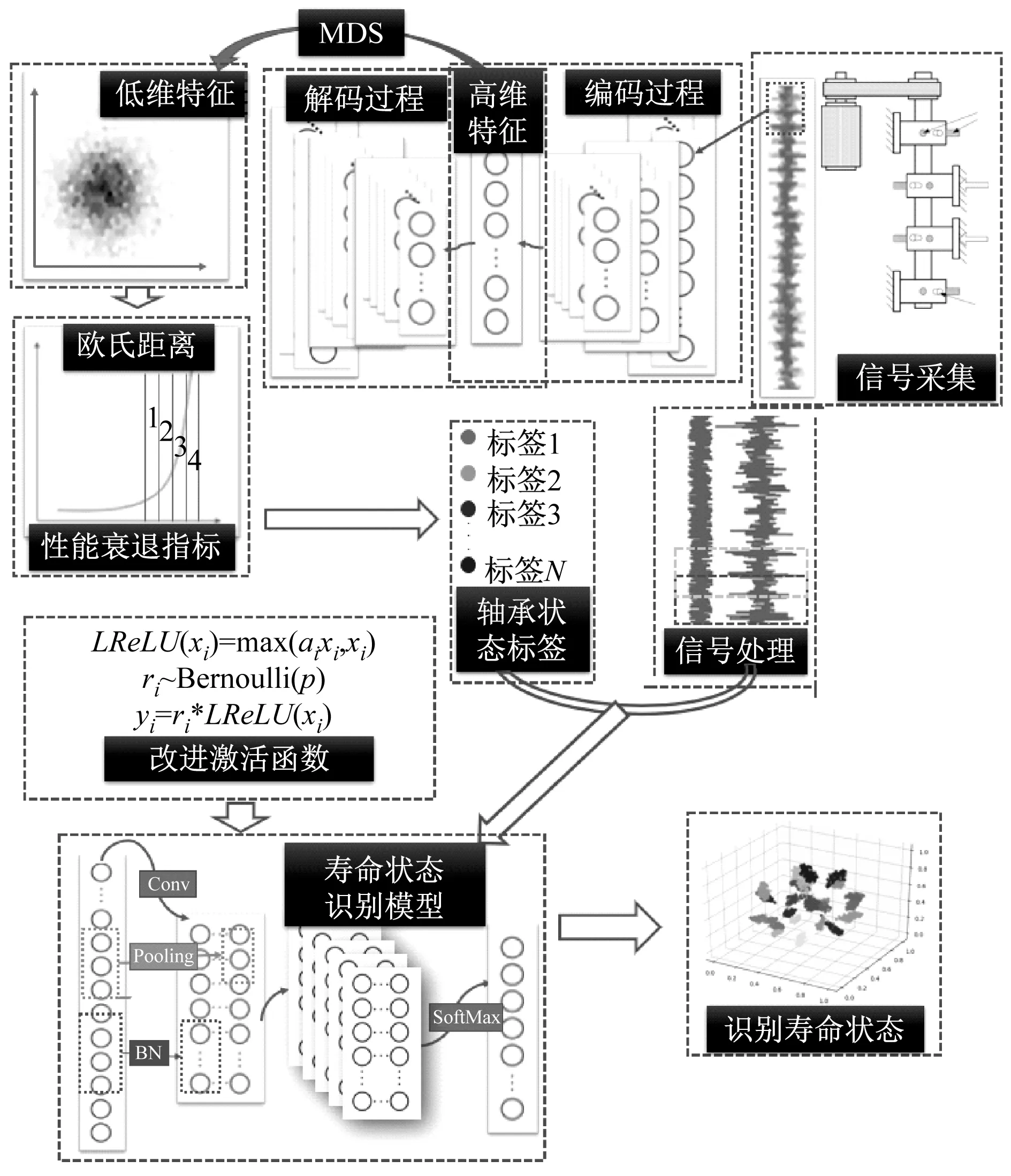
图6 轴承寿命状态识别模型Fig.6 Bearing life state recognition model

首先，将预处理过的轴承振动信号通过CAE进行处理，自动提取轴承寿命状态特征，再将所提取的特征通过MDS进行约简获得低维特征，在低维特征空间构造欧氏距离作为轴承性能衰退指标。然后，根据标签化轴承数据训练改进的CNN轴承寿命状态识别模型。在训练过程中，为抑制过拟合，对原始训练样本进行加噪、重叠采样处理，为提高模型抗干扰能力，将LReLU函数和Dropout作为激活函数。

4 滚动轴承性能评估与寿命状态识别

本节中，将数据集2中第2组轴承测试中的第1个轴承的x轴数据以证明所提方法的有效性。从测试中捕获信号，构建轴承性能衰退指标，根据标签化的数据训练模型。最后，将测试的识别结果与其他方法的结果进行比较。

4.1 创建轴承性能衰退指标

在获取和处理完之后，将样本数据导入CAE模型进行特征提取。本文中的CAE共9层，参数见表1。表中，所有Resize层插值方式是双线性插值。Fully-connection1的结果作为样本降维之后的结果。

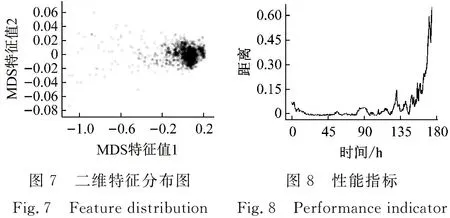
图7为CAE-MDS提取特征后的二维特征分布，颜色越深的区域为特征点越集中的区域。本文中，CAE-MDS算法以全寿命的样本作为输入，图7中包含了正常期、衰退期的数据。一般来说，轴承信号会有一段较长的正常期，因此，图7中颜色较深的中心区域就是正常期轴承信号提取特征后的特征点分布，越向外特征点偏离正常期样本域中心，进入衰退期。图7通过CAE-MDS的提取特征方法，有效的展示了正常期、衰退期样本域的分布情况，使得正常期、衰退期样本域特征被很好地表征。由图7可获得轴承正常期样本域中心，取该中心作为基准数据。在二维中，计算其他样本与基准数据的欧氏距离，即是本文中采用的轴承性能衰退指标，得到图8。

表1 本研究所提出的CAE模型参数

4.2 数据标签化

在建立轴承寿命状态识别模型之前，需要确定衰退期，完成以寿命状态为标签的标签数据。CNN根据标签提取衰退期信号中的特征，得到最终的寿命状态识别模型。一般情况下，实验轴承刚开始采集的信号不稳定，因此，本文中规定在实验开始的第二天到第三天的最大欧氏距离值为阈值，连续10个欧氏距离值超过阈值的点为衰退期起始点，以实验结束时为衰退期结束点。衰退期起始点为0.03，衰退期结束点为0.65。在衰退期起始点之前是正常期，衰退期起始点、结束点之间为衰退期，将整个衰退期按时间均匀的划分，文中分别划分了12类和24类，图9是12类数据集的划分，每类500组数据，每组4 096个数据点，每类都可以的认为是一个退化阶段。在固定长度的衰退期内划分的越多，意味着识别难度越大，这是因为类别数越多，每一类的样本数越少，相邻两个类别的间隔时间越短，轴承信号的相似度越高，识别难度就越大。

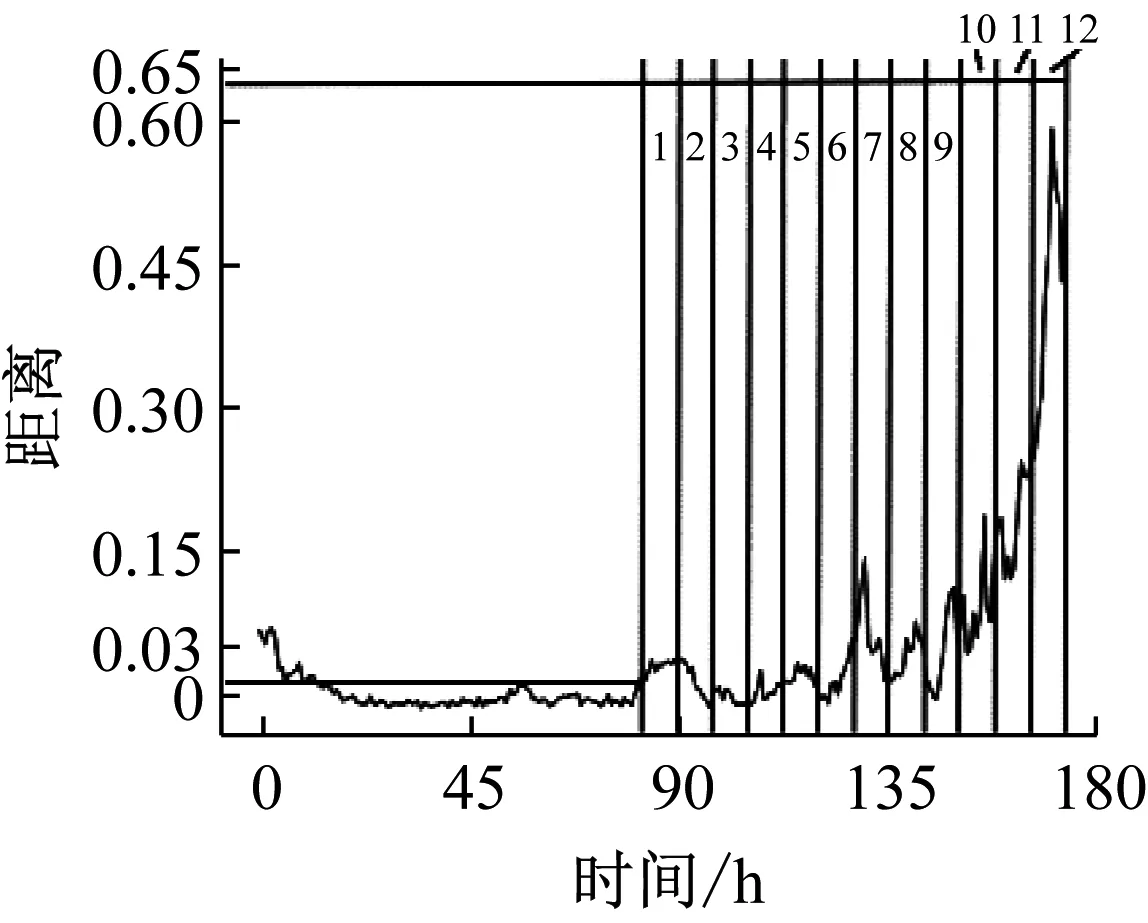
图9 12类别数据集的划分Fig.9 Classification of 12 categories of data sets

4.3 本文CNN模型结构参数

CNN模型各层的参数见表2。

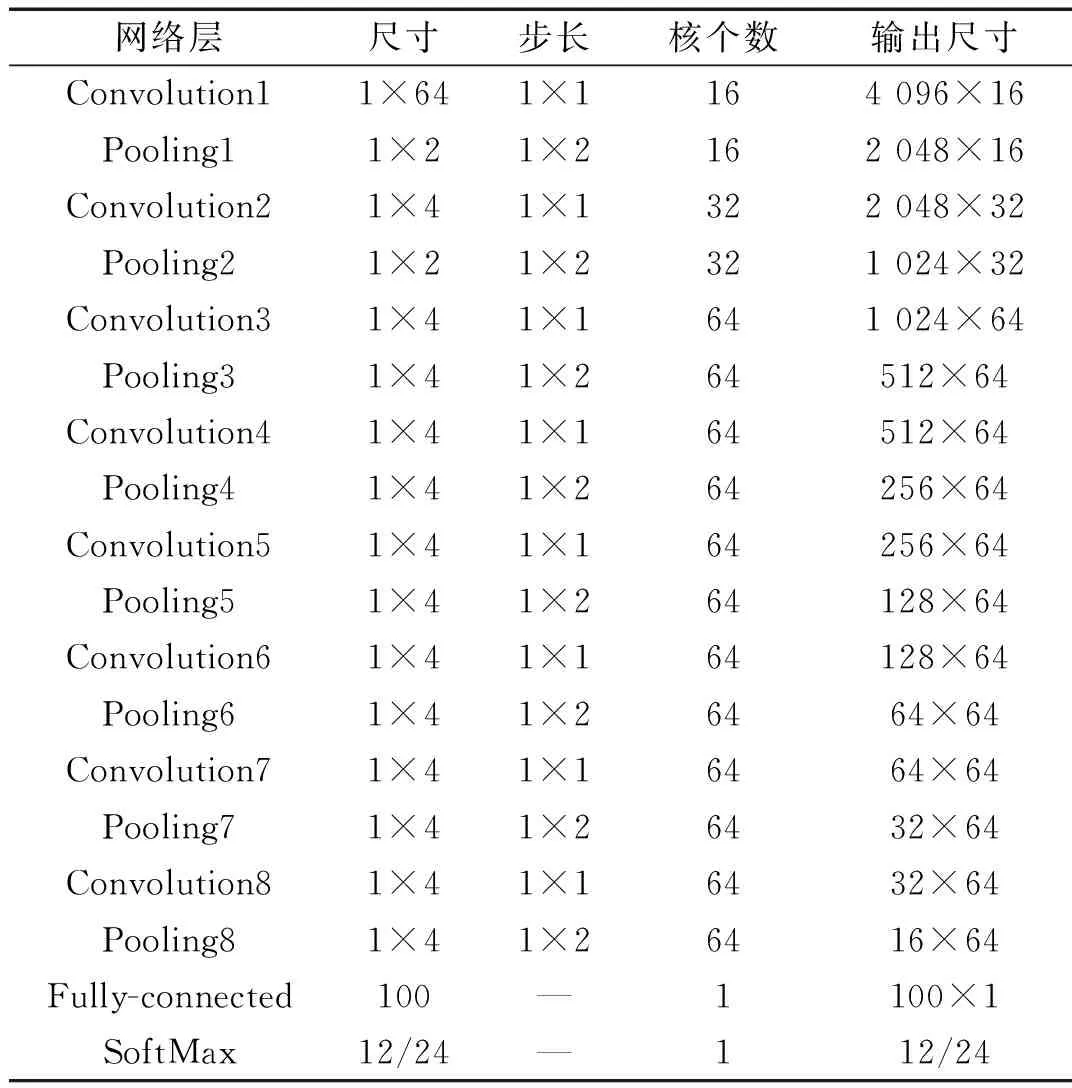
表2 本研究构建的CNN模型参数

在实验中使用的所提出的CNN结构由8个卷积和池化层组成，紧接着是全连接层和SoftMax层。实验使用Google的Tensorflow工具箱实现。第一个卷积内核的大小为1×64，合适的第一个卷积内核可以起到抗干扰作用[15]，其余内核大小为1×4，激活函数为LReLU和Dropout的组合，为了减少运算量在全连接层运用ReLU为激活函数。池化类型为最大池化，在每个卷积层和完全连接的层之后，批量归一化用于改善CNN的性能。实验中分别做了12、24分类模型。

4.4 结果与比较

为了证明所提出方法的优点，本文使用标准CNN进行比较，还与其他传统方法来分析相同的数据集，包括支持向量机(SVM)、深度置信网络(DBN)等，各个方法对轴承磨损程度的识别正确率见表3。

表3 不同分类模型识别正确率

从表3可以看出，本文所提出的方法在0 dB环境下的正确率比其他传统方法具有更高的精度。主要原因是CNN相较于BPNN、DBN等神经网络在提取局部特征上的能力更强，卷积运算使得CNN能够更加有效地从输入数据中学习细节特征。CNN相较于SVM传统智能方法在自动提取复杂特征上的能力更强，传统智能方法的性能在很大程度上依赖于手动特征提取，在从原始特征集中选择最敏感的特征或设计具有优异特性的新特征后，其诊断结果将得到进一步改善，然而，这是一项盲目和主观的任务。与部分神经网络和传统智能方法相比，CNN的自动特征学习能力更强大。

另外，为验证所提出改进部分的优越性，进行不同噪声环境试验、12分类和24分类试验，以分析不同模型的性能。为验证样本加噪对模型的影响，表4比较了不同噪声下12分类模型识别正确率。表4中，A表示文中所提出的方法，训练样本加噪，12分类，激活函数中Dropout率为100%，神经网络节点全部存活；B表示传统CNN，训练样本加噪，12分类；C表示传统CNN，训练样本未加噪，12分类。传统CNN的参数和改进CNN除了激活函数不一样，其他的参数和结构都一致，改进模型的激活函数是LRULE，传统CNN模型的激活函数是RULE。

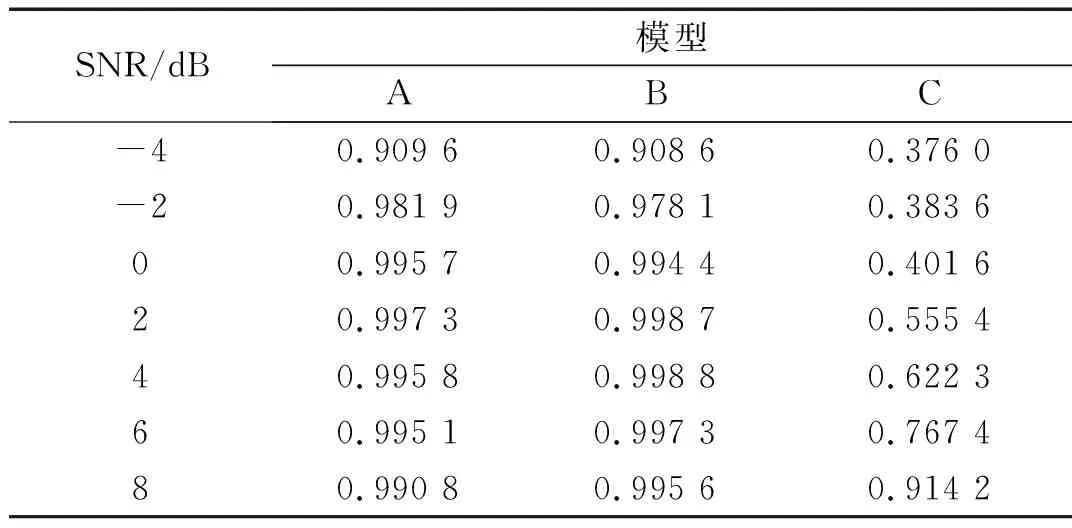
表4 不同噪声下12分类模型识别正确率

表4示出了在SNR值为-4 dB～8 dB时，所有模型具有较高的识别准确度。然而，随着噪声加强，传统的CNN模型的准确度显着降低。当测试样本的SNR低于1 dB时，传统的CNN的精度低于50%，而即使在SNR值为-2 dB～8 dB的样本上进行测试时，所提出的CNN的准确度仍然高于95%。这表明样本加噪训练方式有效的抑制了模型过拟合。在0～8 dB环境下，模型A和模型B的识别率相差仅在0.5%以下，且正确率都在99%以上。为了进一步验证改进激活函数对模型的影响，模型进行24分类的测试，结果见表5。表中，D表示传统CNN，训练样本加噪，24分类；E表示文中所提出的方法，训练样本加噪，24分类，激活函数中Dropout率为80%，节点存活概率为80%；F表示文中所提出的方法，训练样本加噪，24分类，激活函数中Dropout率为90%，节点存活概率为90%。

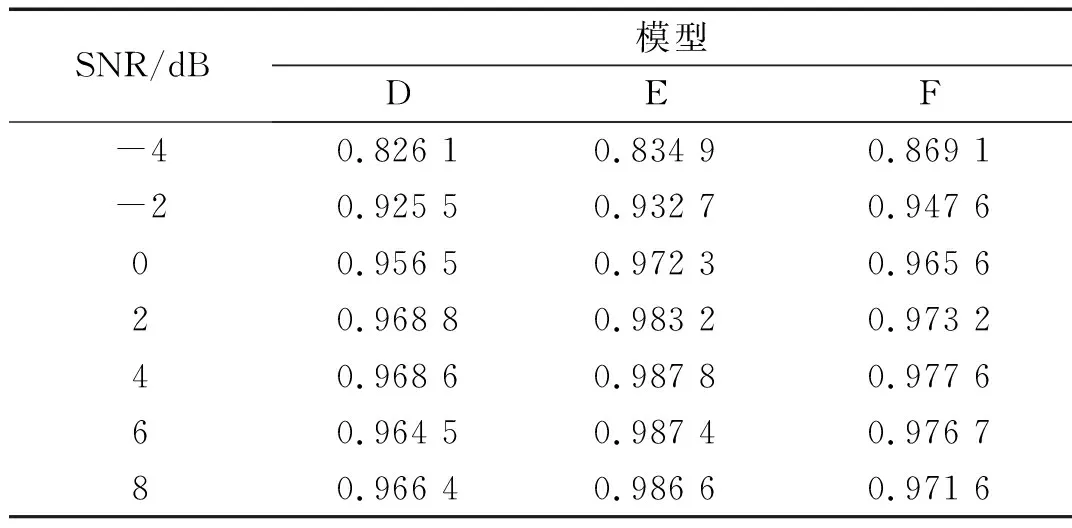
表5 不同噪声下24分类模型识别正确率

从表5中看出，比较模型D与模型E，无论SNR值处于何值，模型E的正确率均高于模型D，验证了针对轴承信号，改进后的激活函数比传统CNN模型中的ReLU激活函数更具有优越性。比较模型E、模型F，在-4 dB～-2 dB噪声环境下，模型F的识别率较高，在0 dB～8 dB噪声环境下，模型E的识别率较高。因此，改进激活函数选择合适的Dropout率能使模型能够更好的提取特征，有更好的识别正确率。该结果验证了改进模型的优越性。

5 结 论

(1) 本文通过CAE与MDS算法完成了轴承寿命状态特征的特征与表达，并构建了轴承性能衰退指标，再根据构建指标和改进卷积神经网络建立了轴承寿命状态识别模型，实现了轴承寿命状态识别。

(2) 针对在噪声环境下的轴承信号，LReLU与Dropout组合的激活函数比ReLU激活函数更具有优越性，提出的带有Dropout结构的模型相比别的模型对噪声的容忍度更高，提出的训练数据加噪的方法有效的抑制了神经网络过拟合问题。

(3) 验证结果表明相较于其他模型，所提出轴承寿命状态识别模型具有更好的抗干扰能力，能更好实现对轴承实验数据寿命状态的识别。