基于注意力BiGRU的机械故障诊断方法研究

张立鹏，毕凤荣,，程建刚，沈鹏飞

(1.天津内燃机研究所，天津 300072； 2.天津大学 内燃机燃烧学国家重点实验室，天津 300072)

国民生产环节中，机械生产设备连续化、高速化、自动化的趋势迅猛发展，因此监测设备运行状态、保障重大产品设备安全稳定运行、防止设备故障带来的经济故障和人员伤亡变得愈加重要。状态监测与故障诊断技术作为一门迅速发展的工程领域技术得到科研人员的广泛关注。

基于振动信号的故障诊断方法，由于其测量简单、成本低、采集精度高、适应性强等优良特性，在工程实践中被广泛应用[1]。基于振动信号的机械状态检测与故障诊断一般包括特征提取和模式识别两个阶段。当机械系统如轴承等关键部件发生故障时，瞬时冲击响应成分将通过结构传播到传感器，储存于采集到的信号数据中，这种成分表现出持续时间较短、频带较宽等特点，通过分析处理这种带有时变特性的非平稳信号，便可以得到机械的故障类型。目前，处理和分析非平稳信号时，短时傅里叶变换(short time transform,STFT)、小波变换(wavelet transform,WT)、稀疏表达[2](sparse representation,SR)、经验模态分解[3](empirical mode decomposition,EMD)、变分模态分解[4](variational mode decomposition,VMD)等方法都取得了不错的效果，对于特定的故障类型实现了较好的分类准确性，但都存在自适应性差、算法复杂、过于依靠先验知识、过于依赖所提取特征的质量等局限性。

随着深度学习的兴起，基于神经网络的人工智能模型被引入机械故障诊断领域。神经网络模型经过不断优化发展，实现了较高的分类准确度，并具有较强的鲁棒性和容错能力，能够充分逼近机械故障类型识别中十分复杂的非线性关系。近年来，循环神经网络(recurrent neural networks,RNN)在时间序列数据特征挖掘领域有着很高的地位，门控循环单元[5](gated recurrent unit,GRU)和长短期记忆网络[6](long short term memory networks,LSTM)等RNN变体在关于时间序列的预测问题领域获得了巨大的成功。本文将以机械故障(以轴承故障和柴油机典型故障为例)振动信号这一典型时间序列预测问题为研究对象，以GRU为主要研究方法，搭建双向门控循环单元(bidirectional gated recurrent unit,BiGRU)网络模型实现“端到端”的机械故障诊断。同时，引入注意力机制，进一步提升模型对于长序列数据的学习能力，实现更优的故障诊断效果。

1 算法原理

1.1 循环神经网络

循环神经网络是用于分析时间序列数据的网络模型，其改变了传统人工神经网络的前馈机制。在前馈型神经网络中，信息经输入层输入，正向输出信息到下一级直至输出层输出结果，整个网络结构中无信息反馈，因此前馈型神经网络没有时间特性，输入之间不相关联，在处理时间序列问题时效果不佳。而对于机械故障振动信号而言，输入信号的特征是有时间关联性的。RNN在前馈型神经网络的基础上引入了时间序列的影响，将隐藏节点定向连接成环，这样有利于网络对时间信息的传递，展示动态时序行为，进而挖掘时间序列的特征[7]，其示意图如图1所示[8]。

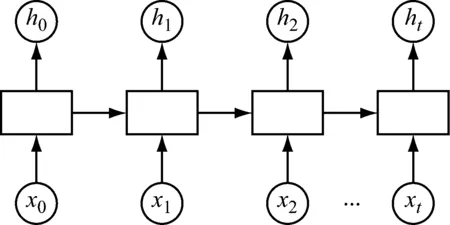
图1 RNN结构示意图Fig.1 Schematic of the RNN architecture

RNN的前项传播公式如式(1)～(4)所示。

(1)

(2)

(3)

(4)

式中:x为网络输入;y为网络输出;w为权重;z为神经元的加权和;f为神经网络激活函数;s为神经元激活值;t为网络当前时刻;I为输入向量维度;i为输入向量下标;H为隐藏层单元向量维度;h为t时刻隐藏层单元向量下标;h′为t-1时刻隐藏层单元向量下标;o为输出向量下标。

根据结构图和前向传播公式，RNN隐藏层st不仅取决于当前时刻的输入xt，也取决于上一时刻隐藏层输出st-1。表现出RNN不仅能接收到当前时刻样本的信息，也能接收上一时刻的信息，即RNN具有了时间特性。将式(1)～(3)迭代入式(4)，可以得到式(5)，表示最终时刻的输出结果包含了整个时间序列的特征信息。

(5)

1.2 双向门控循环单元

门控循环单元神经网络是RNN的一种变体，其利用特殊的“门”结构作为记忆单元替代了传统RNN的神经元结构，解决了RNN在处理长时间序列时因梯度消失而易陷入局部最优的问题。

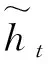
rt=σ(Wrhht-1+Wrxxt)

(6)

zt=σ(Wzhht-1+Wzxxt)

(7)

(8)

(9)

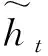
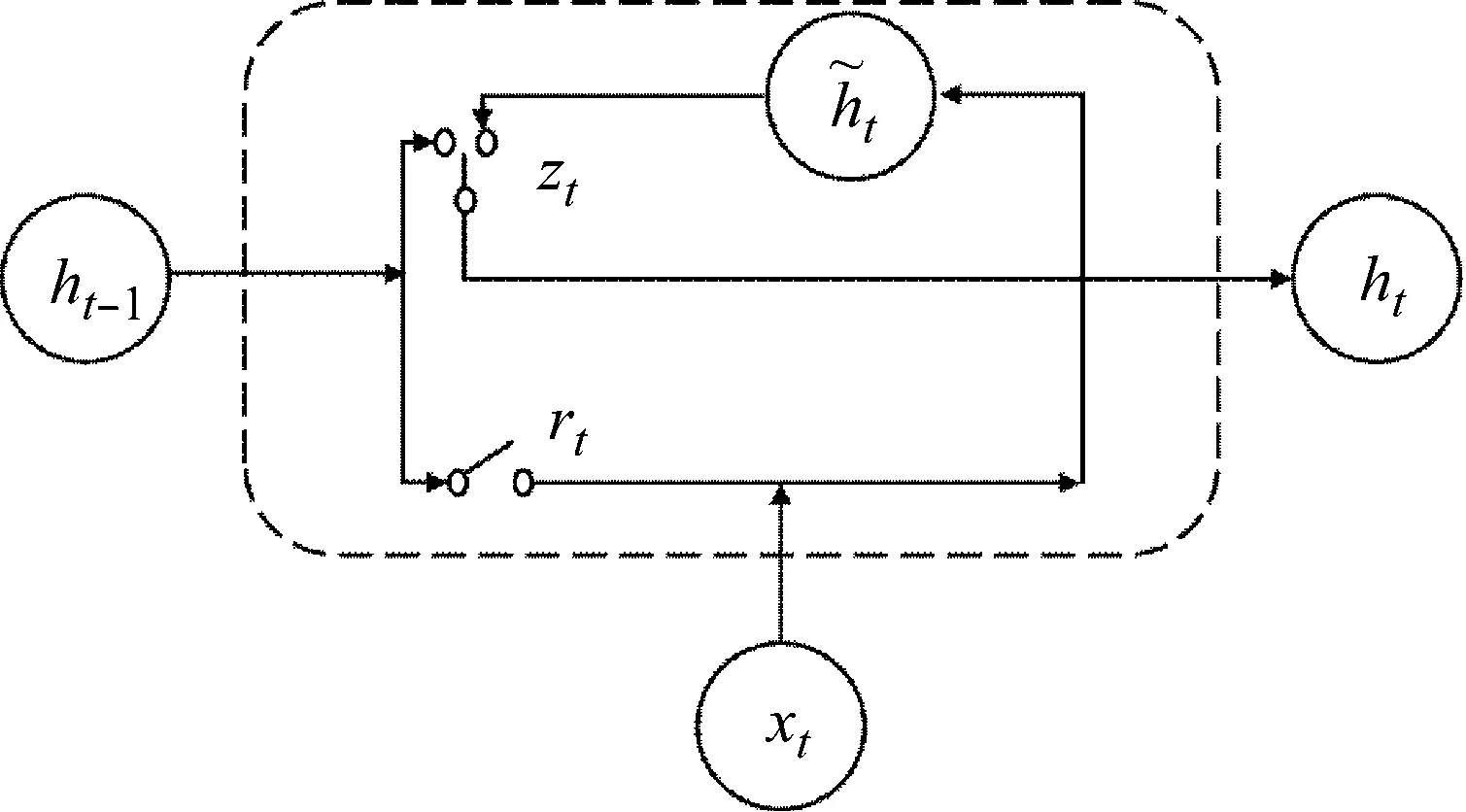
图2 GRU内部结构Fig.2 Inner structure of GRU

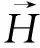
(10)

1.3 注意力机制

注意力机制在自然语言处理[11]、图像分类[12]、文本分类[13]等任务中都取得了成功。本文将注意力机制引入故障诊断领域。具体地，对于BiGRU网络的各时间节点输出H=[h1,h2,h3…,hL](L表示序列长度)，通过分配一个权重系数S=[s1,s2,s3,…,sL]。可以有选择性地关注整个序列数据中的不同位置信息。详细原理如式(11)所示

H′=tanh(H)

S=softmax(αTH′)

y=HST

(11)

式中：α为可学习参数，采用随机初始化方式给点初始值，通过反向梯度下降算法计算；y为最终输出结果。可以发现，最终输出y不再单纯依赖最后时间节点输出，而是综合各个时间节点输出的结果。注意力机制的引入，可以有效地解决BiGRU对于过长序列数据学习效率低的问题。

2 基于注意力BiGRU的故障诊断模型

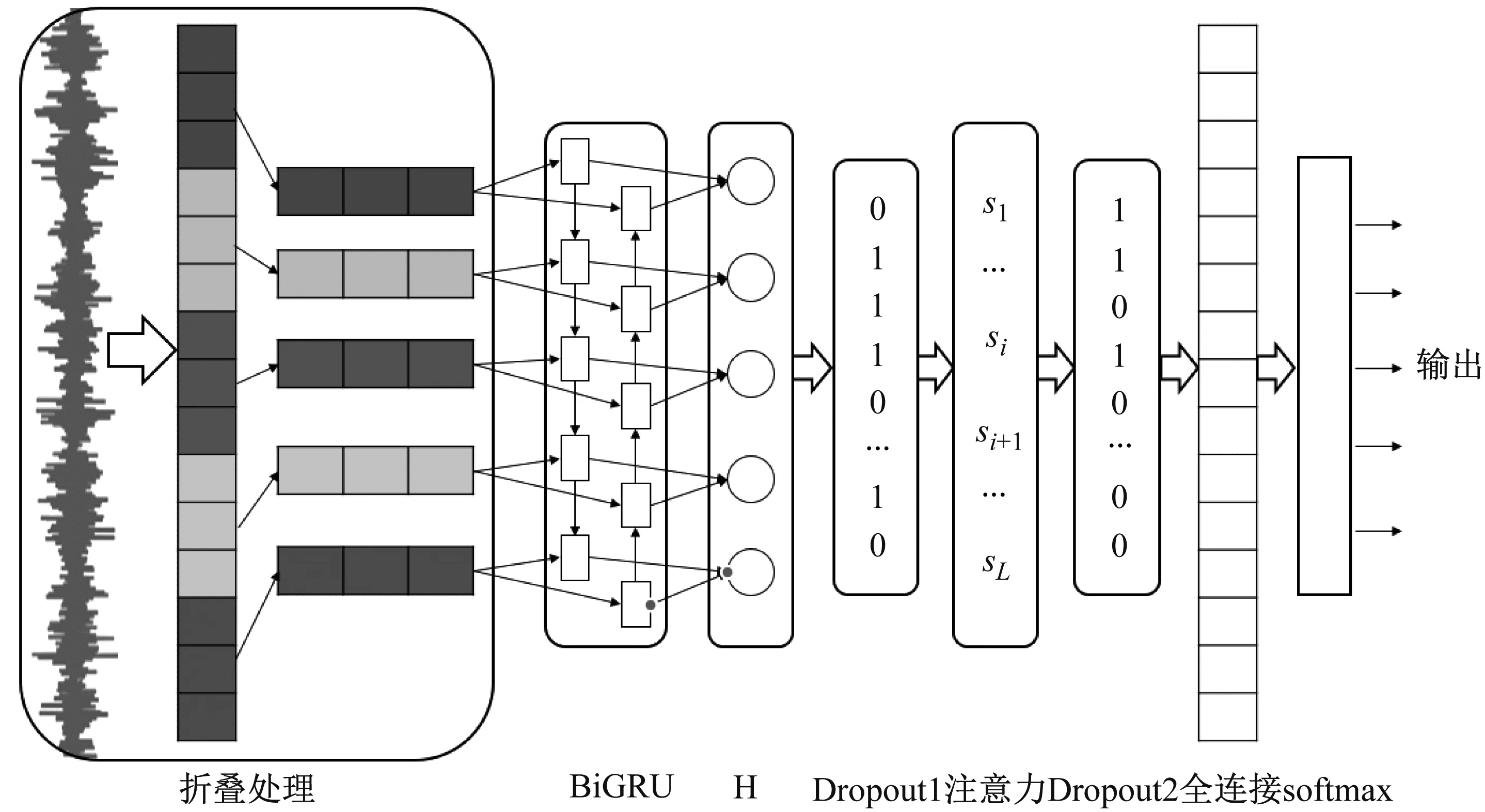
图3 基于注意力BiGRU的故障诊断模型Fig.3 Fault diagnosis model based on attention BiGRU

3 实例分析

3.1 数据集介绍

本文将在公开数据集——美国凯斯西储大学轴承数据集，以及柴油机实验故障数据集上验证模型的有效性。

其中美国凯斯西储大学数据实验包含内圈故障、滚动球故障以及外圈故障(3点钟、6点钟、12点钟位置)，故障损伤直径分别为0.007、0.014、0.021和0.028英寸(1英寸=2.54 cm)。本文将选用正常、内圈故障、滚动球故障以及外圈故障(6点钟方向)4种状态数据，每类故障状态包含损伤直径为0.007、0.014、0.021英寸的3种故障程度，因此共包含10类故障状态。

采样频率为48 kHz，电机工作转速为1 750 r/min。轴承每转一圈采样点数为1 646，为保证每个样本均包含一个完整的周期，本文将样本长度定为1 680。为增加神经网络训练数据量，本文将用重叠采样的方式对原始数据进行截取。对于训练数据，重叠率为50%，对于测试数据，将采用无重叠方式截取。最后共得到10类样本数据，每类数据包含376个训练样本和100个测试样本。在轴承数据集中，样本长度为Lb=1 680，取db=7，则Tb=240。

柴油机故障数据实验在一台某型直列六缸柴油机上进行，该柴油机的性能参数如表1所示。

表1 某型柴油机主要参数

主要采集柴油机的缸盖振动加速度信号，传感器布置在1～3缸的缸盖上，实验柴油机台架示意以及传感器的布置位置如图4所示。

图4 实验用柴油机以及传感器布置Fig.4 The experimental diesel engine and thelocation of the sensors

实验主要模拟了气门间隙异常故障、喷油轨压异常故障、喷油提前角故障以及供油量不足四种故障类型，并且对其中每一类故障发生的不同程度进行了模拟。总共包括13种故障状态，对应样本标签0～12。详细介绍如表2所示(其中气门间隙异常故障数据的两个数字分别代表进气门间隙与排气门间隙，单位：mm)，短线后的数字为对应的样本标签)。设置柴油机转速稳定为1 600 r/min，并且保持满负荷的工作状态，观察测试信号，待其稳定后开始测量并记录数据。

表2 模拟故障工况表

采样频率为25.6 kHz，柴油机转速为1 600 r/min，柴油机每个工作周期采样点数为1 920。于是本文将样本长度设为1 920，保证每个样本内包含一个完整工作周期。同样地，按照轴承数据截取方法进行处理数据。最后获得每类状态数据164个训练样本和50个测试样本。

在柴油机实验数据集中，样本长度为Le=1 920，取de=8，则Te=240。

3.2 实验验证

本文将时域信号直接输入模型，以交叉损失熵为目标函数，通过反向梯度下降算法训练每一层网络参数，每批次训练输入样本数B_S=256，采用指数衰减学习率，学习率LR表达式如式(12)所示。模型各个网络层详细参数如表3所示。

LR=lr*decay_rate(epoch/decay_steps)

(12)

其中：lr=0.01,decay_rate=0.9，epoch为训练次数，decay_steps=40。

表3 注意BiGRU模型参数

将本文模型与单一的BiGRU进行对比，单一的BiGRU模型层数为3，每层隐藏神经元个数依旧为32，在BiGRU输出层紧接一个Dropout层，Dropout比例为0.5。两模型在上述两种数据集上训练对比如图5所示。

如图5(a)所示，在轴承数据集上，经过大约60次迭代训练之后，本文模型便完全收敛，达到了99.95%的训练准确率。但是BiGRU模型经过大约200次训练以后，模型才大致收敛，训练准确率在98%左右，可以看出，在轴承数据集上，和原始BiGRU模型相比，本文模型可以有效缩短三分之二的训练时间，并且取得更好的训练效果，训练也更加稳定。

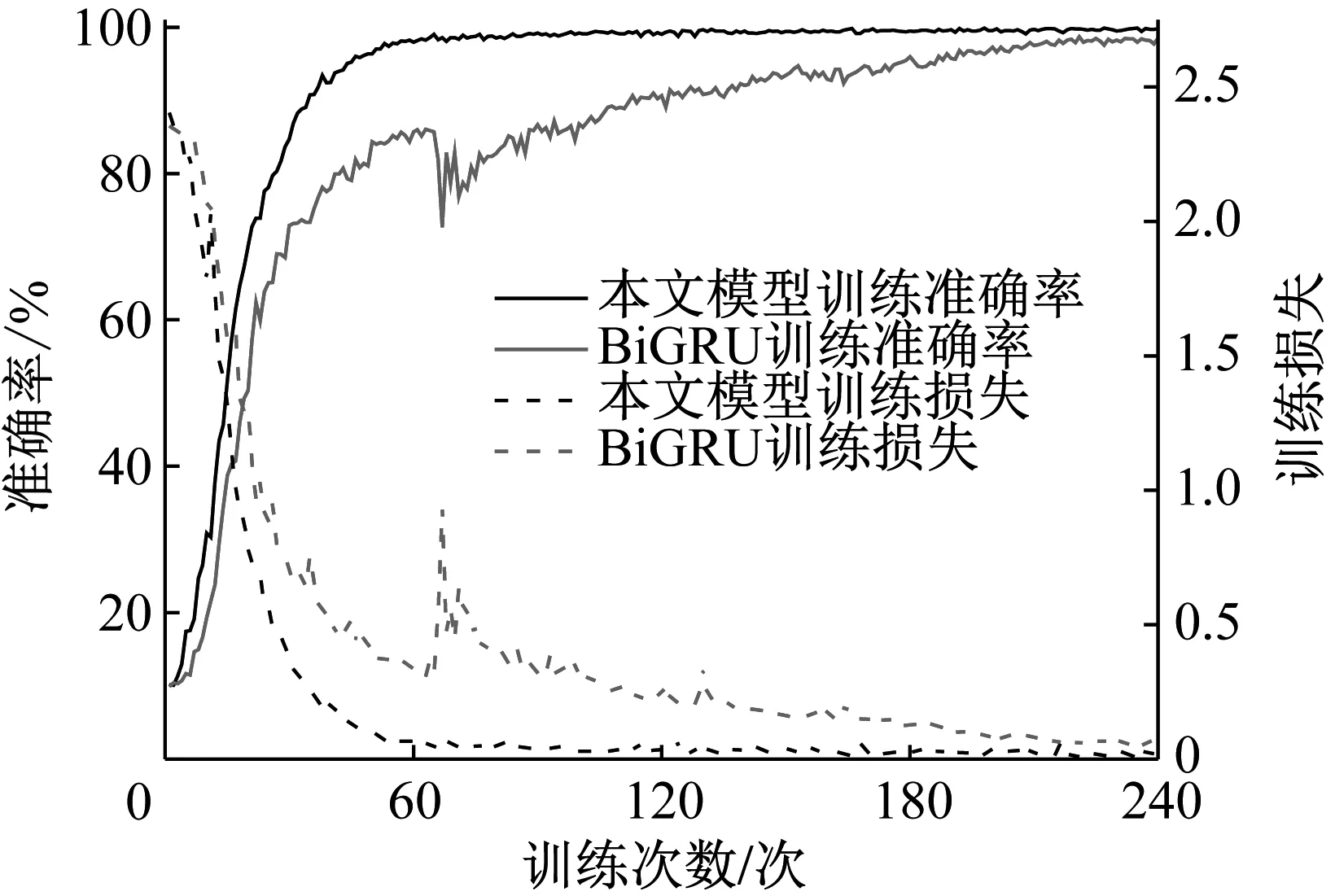
(a) 轴承数据集

(b) 柴油机数据集图5 本文模型与BiGRU训练对比图Fig.5 Training comparison between the attention BiGRU andtraditional BiGRU

如图5(b)所示，在柴油机故障数据集上，本文模型经过了大概90次训练之后便收敛，达到99.82%的训练准确率。但是，BiGRU模型经过大约180次训练以后才大致收敛，训练准确率在98%左右小幅波动，与本文模型训练结果相比，训练损失比本文模型波动也更大，进一步证明本文模型在在有效缩短训练时间的同时能够获得到更佳的训练效果。

测试准确率常用来验证模型的有效性。笔者将分别在轴承数据集和柴油机数据集上测试本文模型和BiGRU模型的测试准确率，测试次数为10次，取平均值作为最终测试结果，具体结果如表4所示。

表4 本文模型与BiGRU测试准确率对比

本文模型在轴承数据集上测试精度比BiGRU高了1.20%，在柴油机数据集上测试精度比BiGRU高了1.69%。不同数据集上的对比结果均表明本文模型具有更高的诊断精度。同时，可以看出，10分类轴承数据集诊断任务难度较低，而13类柴油机故障诊断任务难度较大，但本文模型依旧能够取得91.38%的好成绩。

为了进一步验证本文模型对于原始数据特征的提取能力，本文采用t分布随机邻域嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法对柴油机实验数据集进行降维可视化分析。具体地，分别将柴油机原始时域数据以及本文模型输出数据映射到2维空间，分别命名为t-SNE1和t-SNE2。可视化结果如图6、图7所示。

图6 原始数据特征分布可视化Fig.6 Visualization of raw data features via t-SNE

图7 输出数据特征分布可视化Fig.7 Visualization of output data feature via t-SNE

从图6、图7中可以看出，本文模型可以有效地从原始数据中提取出可分性极佳的数据特征。图6中的各类数据特征相互重叠，无法直接进行区分。经过本文模型的自适应学习处理之后，可以得到聚类特征非常明显的结果。也进一步证明了本文模型可以从原始数据特征中提取出具有明显差异的数据特征。

3.3 鲁棒性分析

抗噪能力是评估模型性能的一个重要指标。为进一步测试本文模型在噪声干扰下的精度变化情况，将采用3.1节所述轴承数据训练集对本文模型进行训练。然后在3.1节所述轴承数据测试集中添加不同信噪比的高斯白噪声，用于测试模型精度，信噪比范围为-4～10 dB。信噪比定义如式(13)所示，本文模型和BiGRU对比结果如图8所示。

(13)

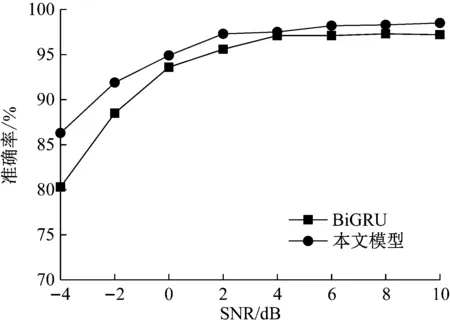
图8 各模型在不同噪声环境下测试准确率Fig.8 Test accuracy of each model under differentnoise environment

如图8可以看出，本文模型在不同噪声环境下表现均优于BiGRU。测试信号混入的噪声越严重，本文模型的精度优势越明显，对于信噪比为-4 dB测试信号，本文模型测试精度比BiGRU高6%。

实验结果表明本文模型对于噪声干扰具有鲁棒性，该效果得益于注意力机制的引入。原始BiGRU模型中，最终结果完全依赖最后时间节点隐藏状态输出，其对于越早输入网络的信息遗忘越严重。因此，在噪声的干扰下，本就有部分信息缺失的问题导致其分类准确率受到更大影响。但是本文模型通过对各时间节点分配自学习得到的注意力权值以后，使得最终的输出结果可以有效地考虑整个序列信息，能够保留完整序列信息的能力使得其受到噪声的干扰较小，具有更强的鲁棒性。

4 结 论

本文进行了利用振动信号进行机械故障诊断的研究，提出了一种基于循环神经网络的故障诊断方法。该方法首先将采集到的振动信号进行折叠预处理，再利用数据集进行训练，搭建基于双向门控循环单元的神经网络模型，实现了“端到端”的特征提取和故障模式分类过程，同时利用注意力机制进行模型优化，提升了计算效率和诊断准确性。

本文利用美国凯斯西储大学公开轴承数据集和自采集的柴油机故障振动信号进行了方法验证，故障诊断结果表明本方法实现了有效的故障类型诊断，且分类准确性和计算效率相较于模型优化前实现了一定程度的提升，并表现出了更有的抗噪能力。

结果表明，循环神经网络对于解决机械故障诊断类型的时间序列预测问题具有一定的优越性，且对于复杂的柴油机系统仍能表现出良好的性能，循环神经网络及其优化方法在机械故障诊断领域具有巨大的潜力可供挖掘。